经济的快速发展以及不可再生资源的发展受限,促使可再生资源光伏发电得到飞速发展[1-2]。近年来,陆地光伏电站开始大规模建立起来,但是没有更多的土地用来安装光伏电站,这严重制约了陆地光伏电站的进一步发展[3]。为了进一步发展光伏发电,漂浮式光伏(FPV)走进了人们的视野[4]。与安装在陆地上的光伏电站相比,FPV是一种安装在水面上的发电系统,不仅可以节约土地资源,而且还可以冷却光伏组件及电缆,也能够提高发电效率。此外FPV还能抑制水量蒸发、减少藻类生长,也有益于水产养殖和捕捞效益[5]。
相关学者对光伏系统结构进行了优化研究,但主要聚焦于安装在地面、湖泊等静水面上的光伏系统结构上。Ab 等[6]总结了地面太阳能光伏系统结构设计和安装中的问题。高良等[7]通过风洞试验和数值模拟相结合,研究了光伏系统结构支架单元的风场特性。DS等[8]研究了基于非均匀变异遗传算法的太阳能光伏系统结构参数优化。Li等[9]研究并优化了一种新型平板PV/T系统的夹层结构CdfTe薄膜太阳能组件。由于目前陆地和淡水湖泊的条件与海上环境不同,因此应考虑对暴露于海上环境的FPV系统单浮体阵列进行研究,从而设计出一种适用于海洋环境的FPV单浮体结构。
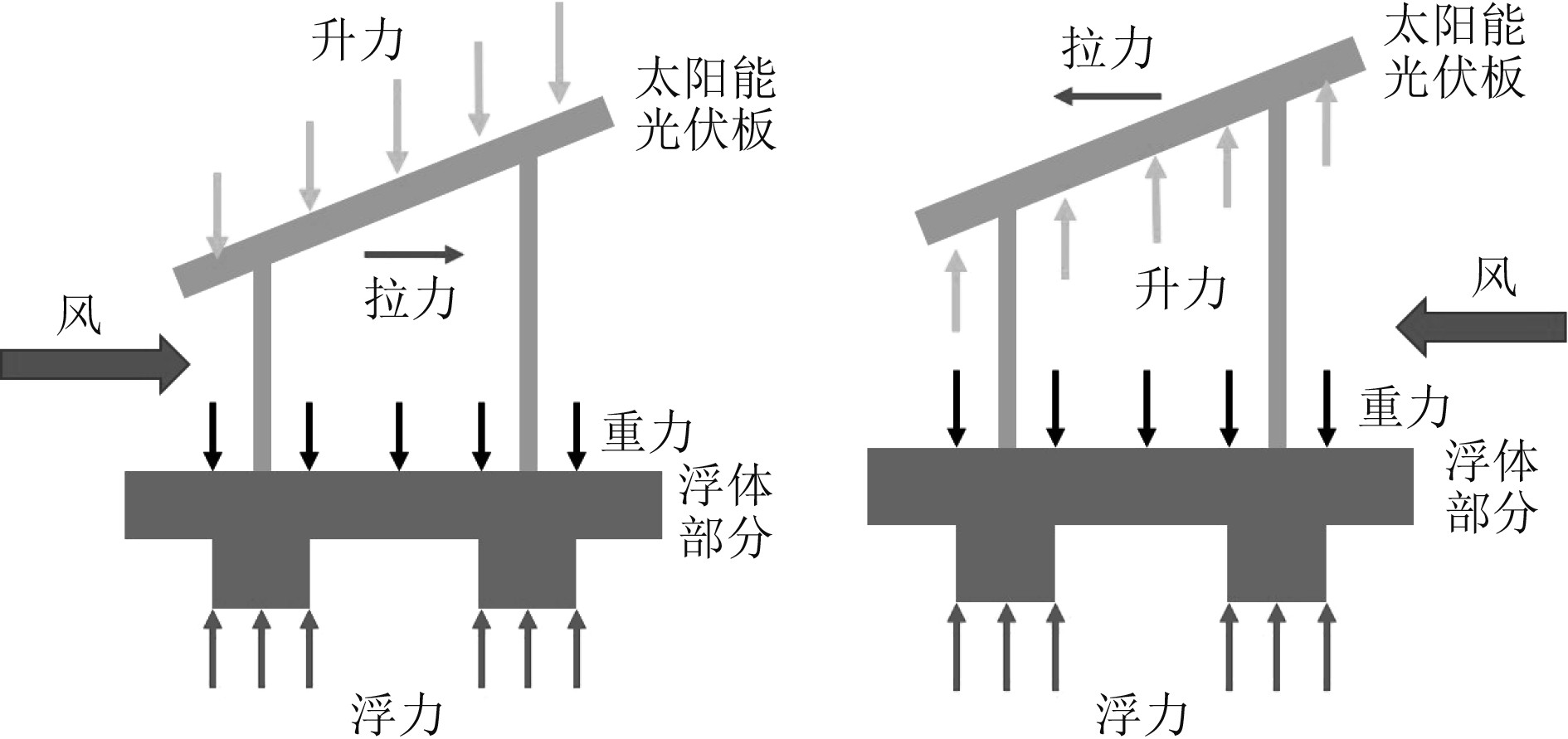
现有的FPV一般放置在天然湖泊、人工水库等水面上,其所受环境荷载小,不需要很强的锚固系统。光伏组件只需提高基础的浮力即可。传统的FPV电站如图1(a)所示,上部分倾斜放置光伏发电板,下部分由轻式泡沫板组成,起到一定的浮力作用。但是如果传统结构的FPV安装到海上环境中,就显得尤为不适应。例如,出现图1(b)所示的结构破坏,这是由于海平面上巨大的风荷载,使得传统结构的FPV非常容易遭到损坏。当光伏发电板安装角度过大的时候,并不能抵抗所有角度的风荷载。所以需要研究出一种新型FPV单浮体结构,以满足复杂的海上环境,抵御风浪流等复杂的环境荷载。提出一种新的FPV浮体结构是设计FPV阵列系统的必要前提,本文着重研究FPV单个浮体结构的受力机理。

|
图 1 FPV电站示意图 Fig. 1 Schematic diagram of FPV power station |
FPV结构在受到风、流、浪的环境荷载下相对于平衡位置作摇摆运动,由牛顿运动定律可得到风、浪、流共同作用下的运动方程[10]为:
| $ \left({\boldsymbol{M}}+{\boldsymbol{m}}\right)x+{\boldsymbol{\mu}} \dot{x}+kx={F}_{z}。$ | (1) |
式中:
风荷载
| $ \begin{array}{c}{F}_{f}={C}_{1}{C}_{2}{P}_{f}S,\end{array} $ | (2) |
| $ \begin{array}{c}{P}_{f}=0.613{{v}_{f}}^{2}。\end{array} $ | (3) |
式中 :
FPV结构在复杂多变的海上环境中,主要受到波浪载荷的作用力。本文采用势流理论方法对漂浮光伏浮体进行波浪载荷计算,假定为理想流体、不可压缩且忽略表面张力、运动是无旋的、存在速度势、水深为常数且水中没有流[10]。
速度
| $ \begin{array}{c}\nabla\varPhi \left(x,y,z,t\right)=0,\end{array} $ | (4) |
流场中总的速度势是由入射波速度势、绕射势和辐射势相互叠加而成的,即
| $ \begin{array}{c}\varPhi \left(x,y,z,t\right)={{\varPhi }}^{I}\left(x,y,z,t\right)+{{\varPhi }}^{D}\left(x,y,z,t\right)+{{\varPhi }}^{R}\left(x,y,z,t\right) 。\end{array} $ | (5) |
式中:
求得速度势
FPV结构湿表面的水动压力
| $ \begin{array}{c}P=-\rho \dfrac{\partial \mathrm{\Phi }\left(x,y,z,t\right)}{\partial t} ,\end{array} $ | (6) |
| $ \begin{array}{c}{F}_{W}=\displaystyle\iint _{{S}_{B}}^{}-P\overrightarrow{\boldsymbol{n}}{\rm{d}}s ,\end{array} $ | (7) |
| $ \begin{array}{c}{M}_{W}=\displaystyle\iint_{{S}_{B}}^{}-P\left(\overrightarrow{\boldsymbol{r}}\times \overrightarrow{\boldsymbol{n}}\right){\rm{d}}s ,\end{array} $ | (8) |
式中:
流速对结构物的作用力为
| $ \begin{array}{c}{F}_{c}=\displaystyle\int_{0}^{h}\frac{1}{2}\rho {C}_{d}{S}{'}{v}_{c}{\rm{d}}z 。\end{array} $ | (9) |
式中:
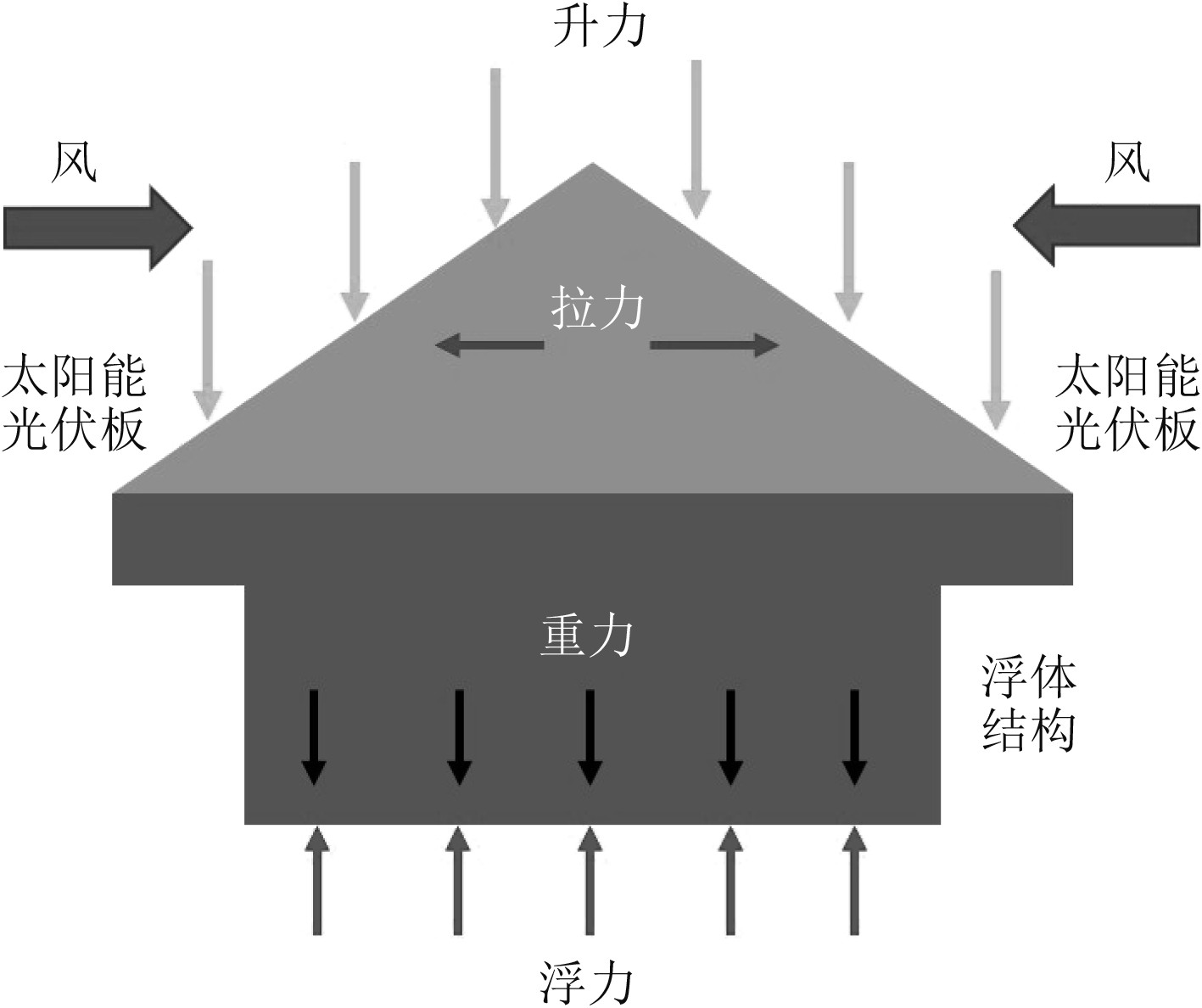
FPV结构主要是由上部的太阳能光伏板和下部的浮体部分组成,太阳能光伏板主要用于光伏发电,浮体部分主要在水面上起到一定的支撑作用。太阳能光伏板上所受到的风荷载通常是FPV结构设计的重要考虑因素。风荷载对于 FPV结构的稳定性尤为重要。如图2所示,FPV结构位于海面或湖泊之上。浮体通过浮力支撑太阳能光伏板,浮力与太阳能光伏板自身的重量相平衡。当风荷载从太阳能光伏板前侧流入时,升力作用在太阳能光伏板的向下方向上,为防止FPV结构因升力而下沉,应增加浮体的浮力。相反,如果风荷载在太阳能光伏板后侧流入时,升力作用在太阳能电池板的向上方向,为了防止FPV结构被升力倾覆,应增加浮体或太阳能电池板的重量。然而,风向无法确定或预测,随时都在变化。为了抵抗不同方向的风荷载,采用两侧呈小角度的安装形式,如图3所示。为了增加整个PFV光伏结构的浮力,结构上部为三角形桁架,两侧呈5°角度安放太阳能光伏板。为了增大排开水液体的量,下部浮体部分采用空腔钢结构体。
|
图 2 原始型FPV光伏组件结构示意图 Fig. 2 Schematic diagram of the original FPV module structure |
|
图 3 新式FPV组件结构示意图 Fig. 3 Schematic diagram of the new FPV module structure |
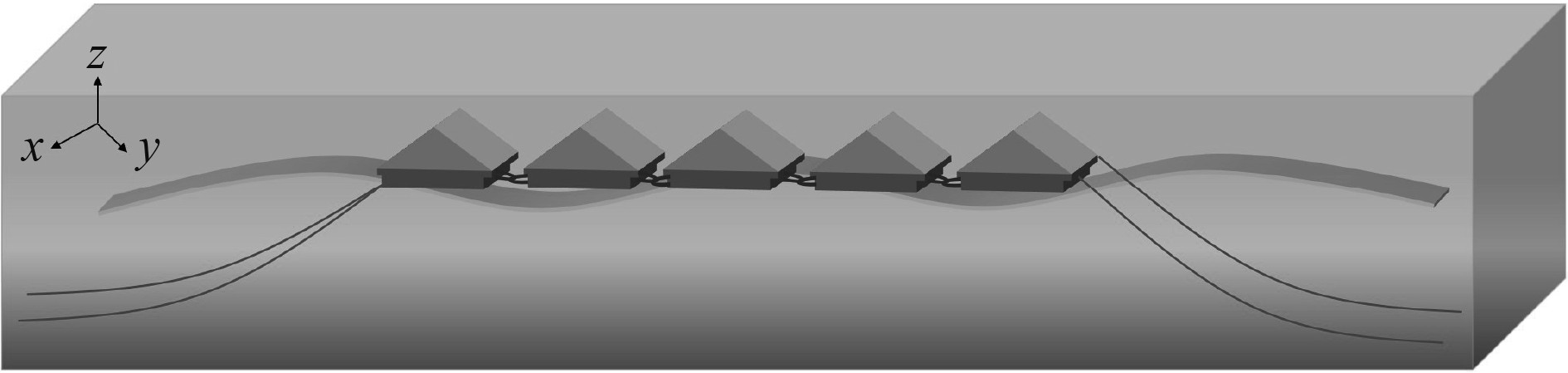
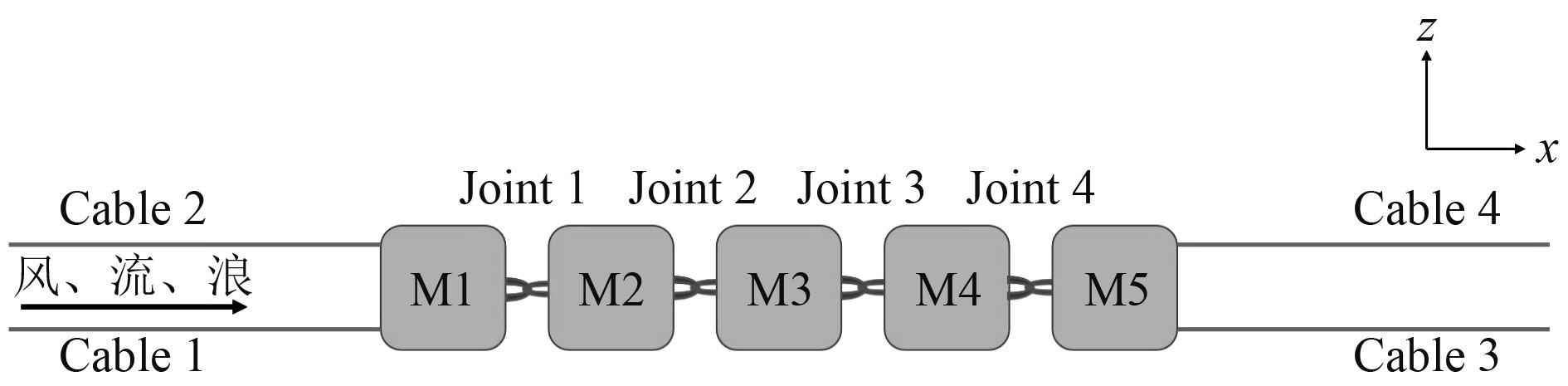
本文研究的海上漂浮式阵列由5个相同模块依次连接成1×5的阵列系统,浮体依次编号M1~M5。模块之间用销绞连接在一起,销绞依次命名为Joint 1~Joint 5,各模块之间间隔为1 m。两端锚链平行与x轴连接至海底,锚链分别命名为Cable 1~Cable 4。详情如图4和图5所示。
|
图 4 FPV阵列系统基础平台模型示意图 Fig. 4 Schematic diagram of the basic platform model of the FPV array system |
|
图 5 1×5阵列FPV系统示意图 Fig. 5 Schematic diagram of 1×5 array FPV system |
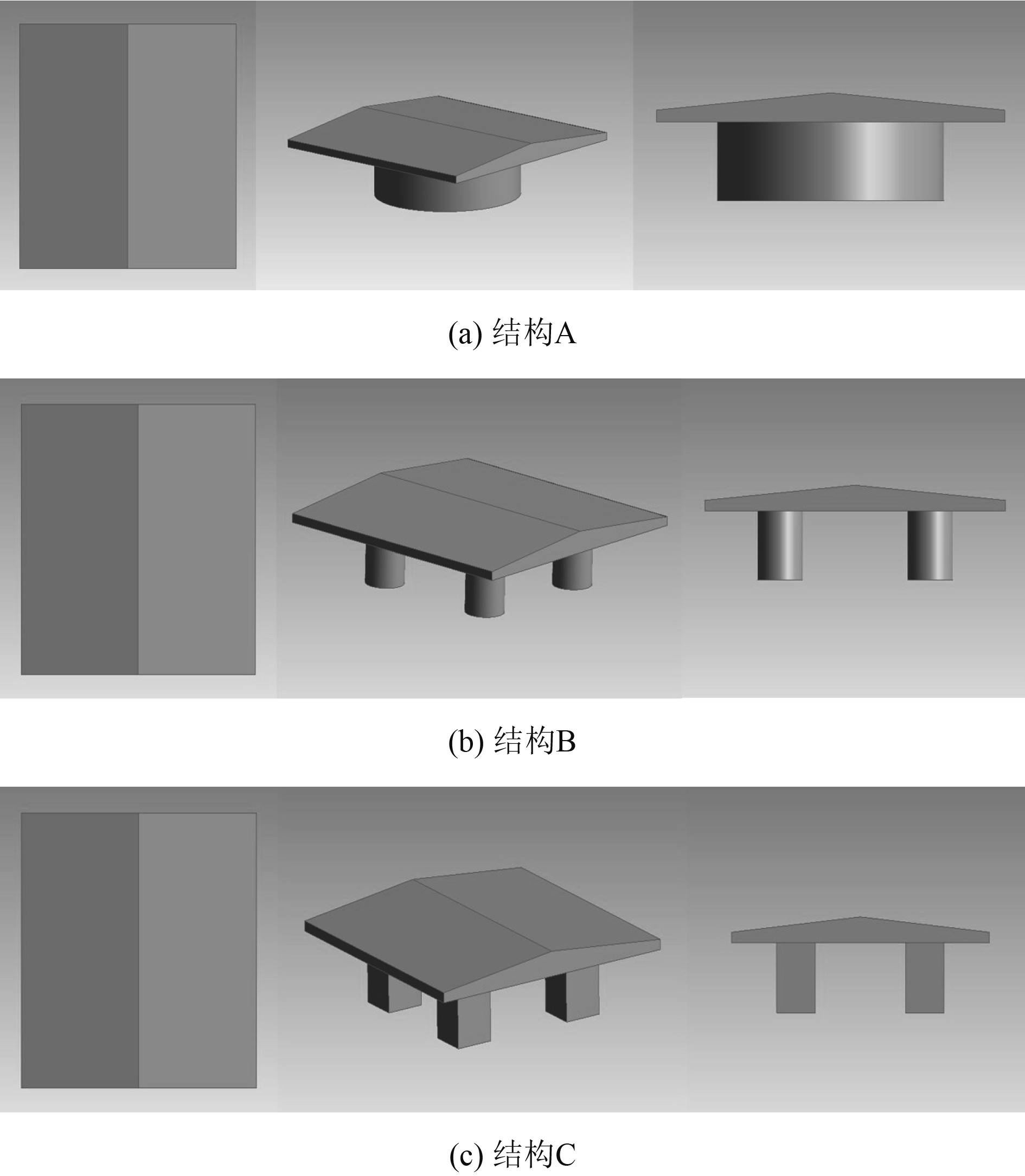
在原始FPV结构的基础之上,提出3种空腔钢材料浮筒式结构,分别是单浮筒式浮体结构、多浮筒式浮体结构和多矩形浮筒式浮体结构,在此称之为结构A、结构B和结构C,简化浮体计算模型如图6所示。模型具体参数如表1所示。
|
图 6 浮体结构示意图 Fig. 6 Schematic diagram of floating body structure |
|
|
表 1 浮体结构参数示意表 Tab.1 Schematic diagram of floating body structure parameters |
安装FPV系统的水深范围为1~17 m,设定水深为18 m。锚链由于坚固耐用且具有良好的抗磨损能力等优点,在浅水区常作为浮式结构物系泊材料。而且,悬链系泊的重量有助于浮式结构物的位置控制,缆绳越重越能够减少浮式结构物的摆动,所以选用R3“全锚链”作为缆绳的材料。锚链的主要参数如表2所示。
|
|
表 2 锚链的主要参数 Tab.2 The main parameters of the anchor chain |
为了研究3种浮体结构在海上环境的稳定性以及端部缆绳的受力机理,定义了6种类型的工况,包含单独风荷载、单独波浪荷载、单独流荷载、风+波浪荷载联合作用、流+波浪荷载联合作用、风+流+波浪荷载6种荷载作用类型。其中风、浪、流速的取值均基于4级海况。风速10.8 m/s,流速2 m/s,波高为规则波,波高3 m,周期6 s,各个工况如表3所示。
|
|
表 3 工况详情表 Tab.3 Working condition details table |
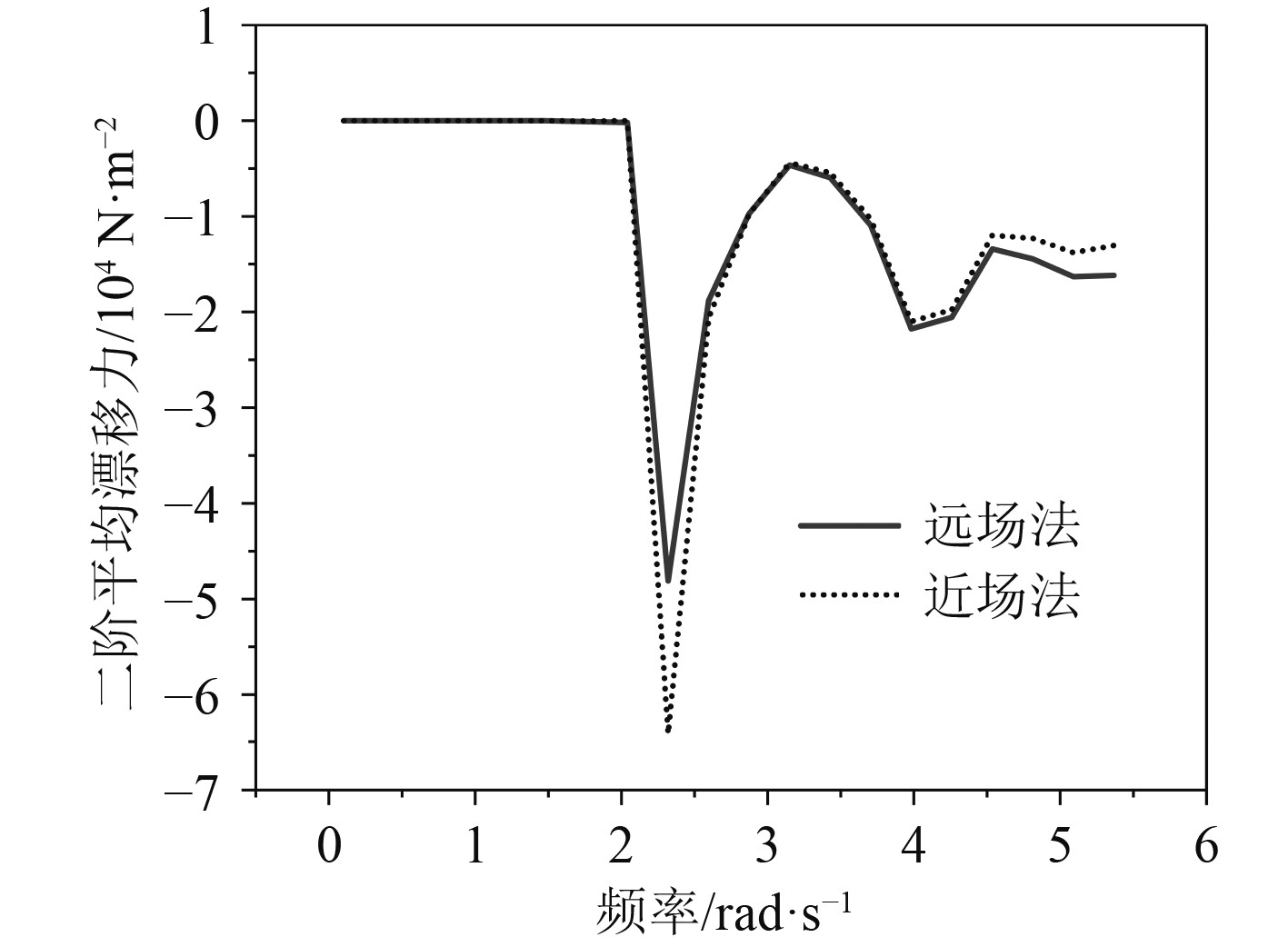
以结构B浮体为例进行网格收敛性分析,结构网格划分示意图如图7所示,总网格数量为6805,绕射单元网格数量为1912,非绕射单元网格数量为4893。采用近场法和远场法分别对横荡二阶平均漂移力进行求解,验证此网格单元划分是否满足水动力计算精度的要求。近场法依赖网格划分,是通过对湿表面的压强积分求解二阶波浪力。而远场法不依赖网格划分,是通过求解动量方程来获得横荡二阶平均漂移力,且远场法求解精度较高。当二者求解结果曲线趋势一致、量级接近时,可认为网格划分能够满足水动力计算精度的要求[12-13],结果如图8所示。

|
图 7 结构网格划分示意图 Fig. 7 Schematic diagram of structural meshing |
|
图 8 横荡二阶平均漂移力 Fig. 8 Sway second-order mean drift force |
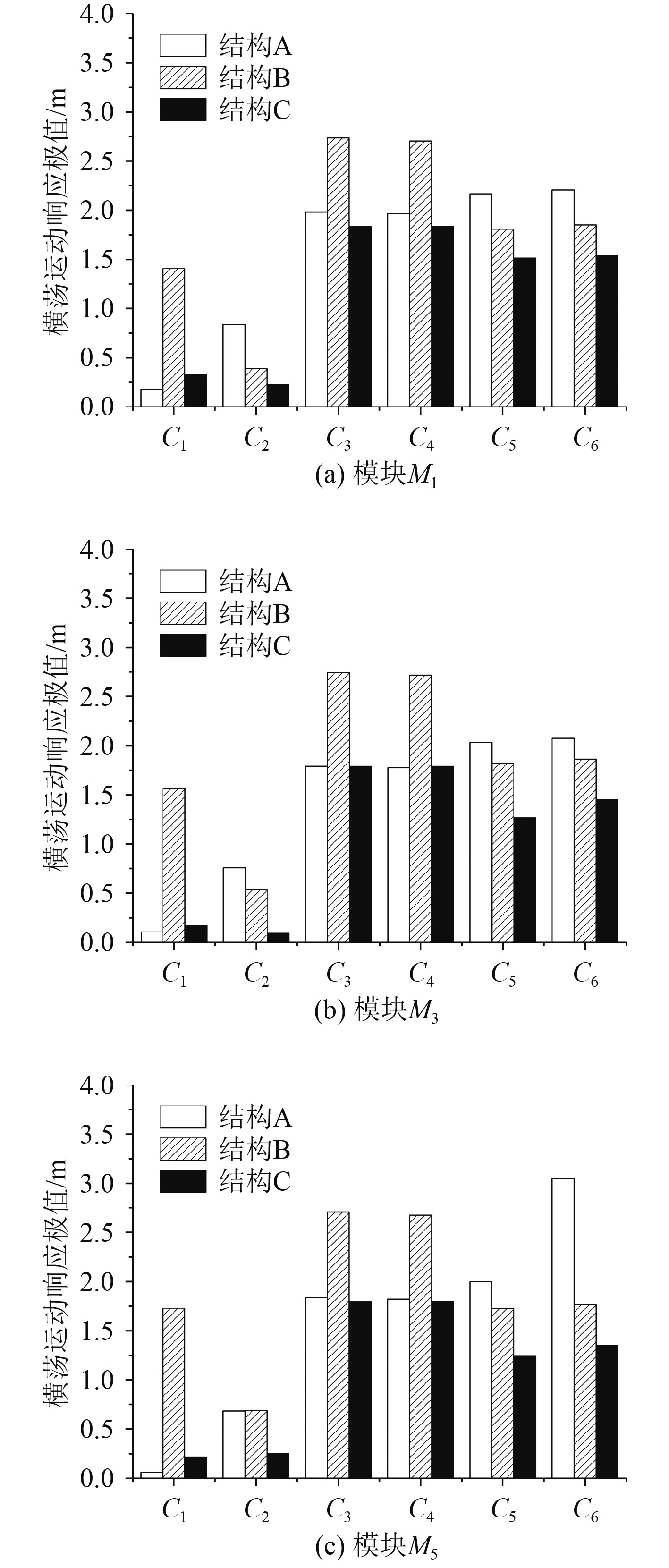
使用Absys软件中的AQWA水动力模块进行非线性时域模拟分析,分别模拟3种不同浮体结构在6种不同工况下的运动响应。由于荷载主要作用于X方向,故Y方向所受荷载较小,浮体结构横摇和纵荡方向的响应值比其他自由度方向较低,所以本文主要研究浮体结构在横荡、垂荡、纵摇和首摇4个方向的运动响应情况。图9~图12给出了结构M1、M3、M5分别在4个自由度方法的响应极值变化情况。
|
图 9 不同结构在不同工况下横荡响应极值 Fig. 9 The extreme value of the sway response of the structure under different working conditions |
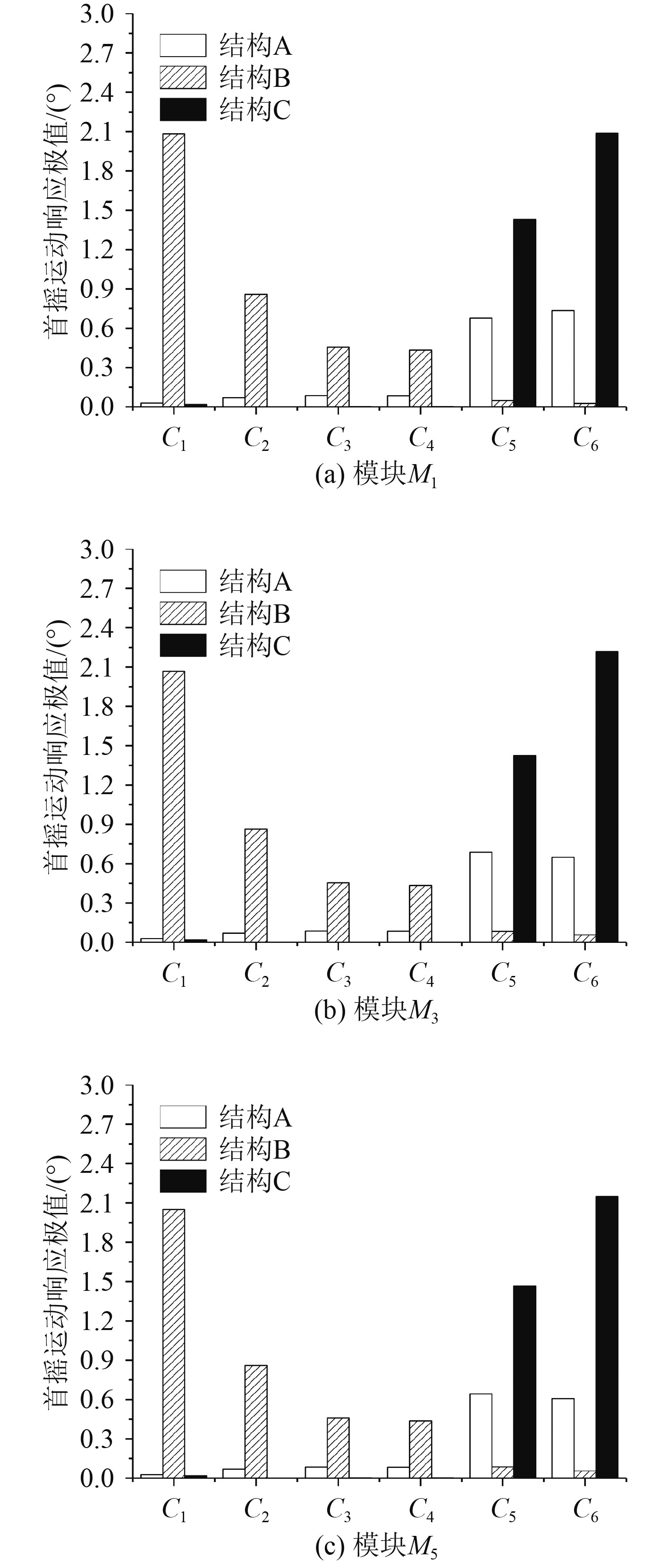
|
图 12 不同结构在不同工况下首摇响应极值 Fig. 12 The extreme value of the yaw response of the structure under different working conditions |
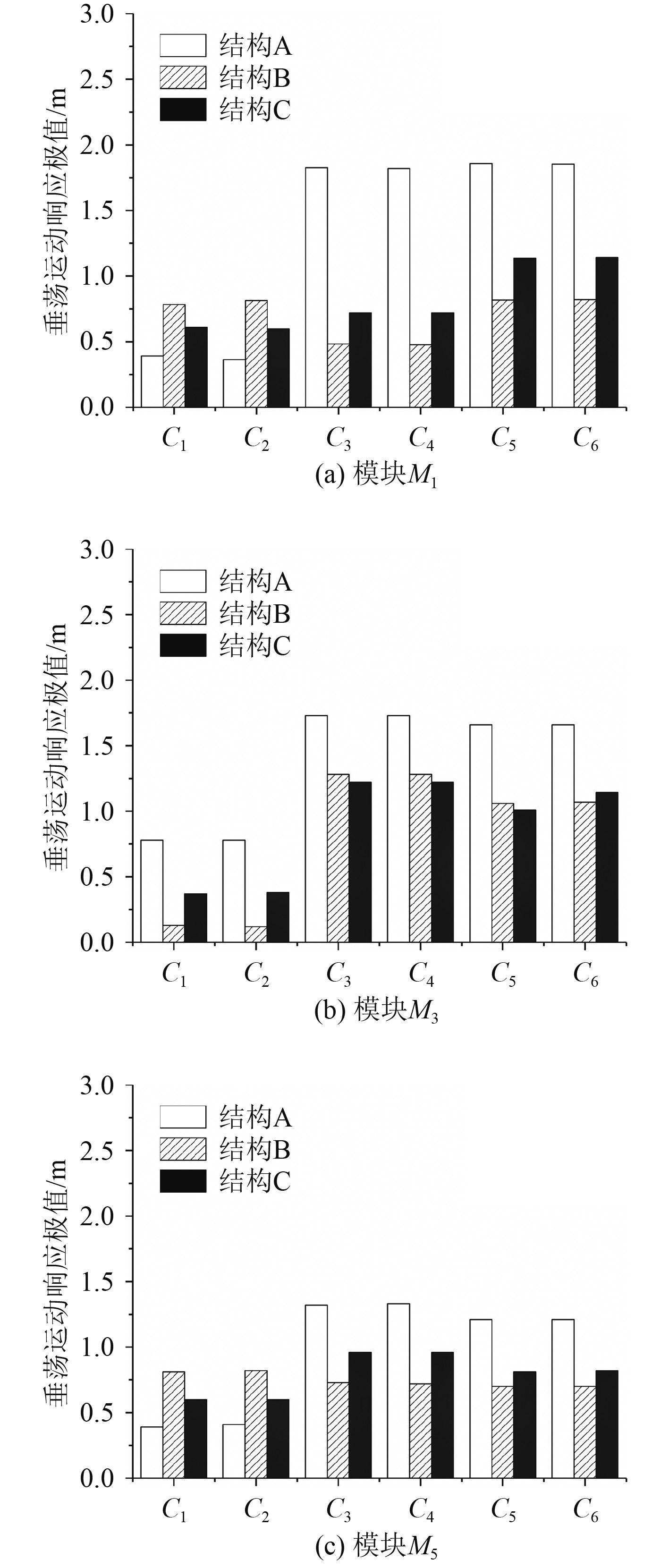
从图9可知,结构B的横荡运动响应值主要是由风和波浪荷载所产生,而结构A和结构C的横荡运动响应值主要是由波浪荷载所引起的。对比工况C3和C5可知,波浪和流荷载耦合作用可以减小结构B和结构C的横荡运动响应,但对于结构A,却使横荡运动响应极值增加。出现这一情况的原因可能是由于结构A的受流面积较大所引起的。图10反映的垂荡运动响应的规律和横荡运动响应类似。
|
图 10 不同结构在不同工况下垂荡响应极值 Fig. 10 The extreme value of the heave response of the structure under different working conditions |
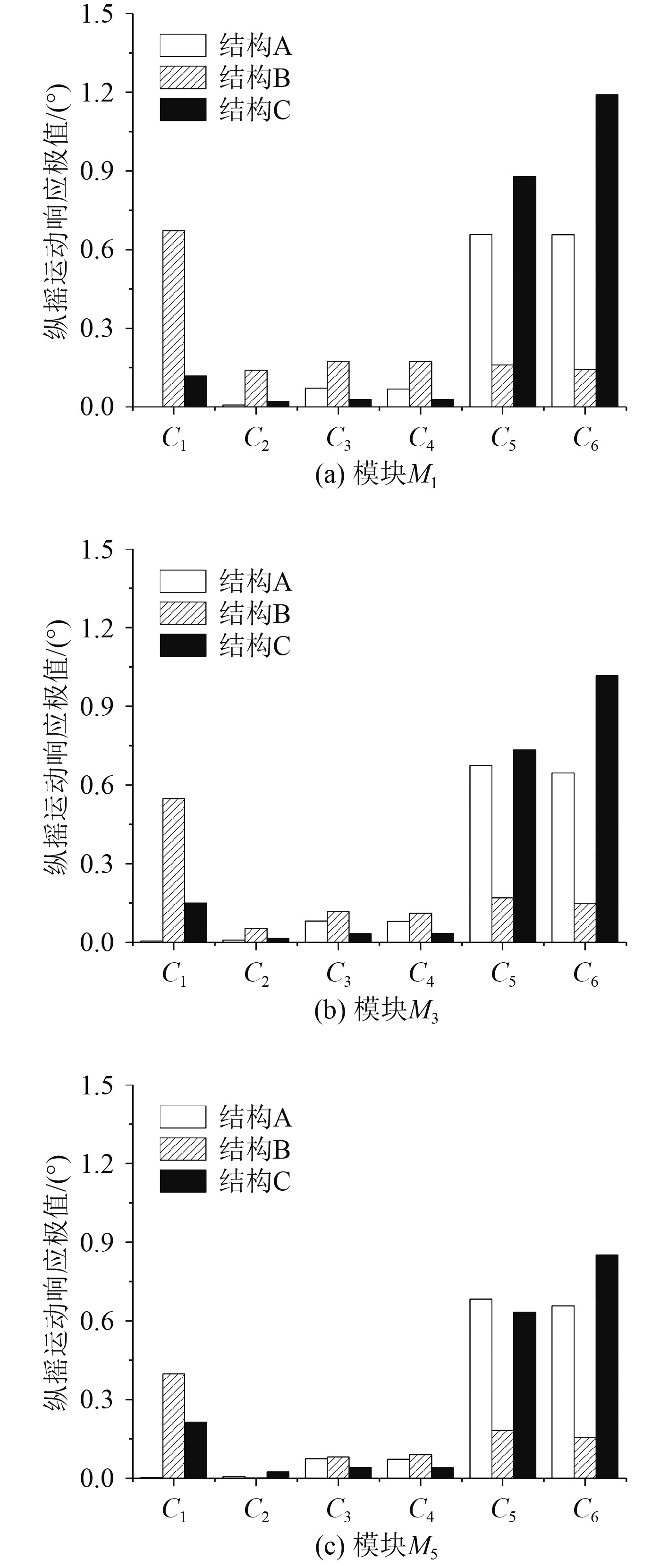
由图11和图12可以看出,结构B纵摇和首摇的运动响应值主要由风荷载所产生,从图12的C1、C4和C6可看出,增加波浪荷载和流荷载耦合都可以减小首摇运动响应;对于结构B和结构C来说,风、波、流耦合荷载所产生的响应最大,结构C最为明显。
|
图 11 不同结构在不同工况下纵摇响应极值 Fig. 11 The extreme value of the pitch response of the structure under different working conditions |
由于环境荷载主要是从0°方向加载,所以主要考虑迎浪侧的锚链受力情况。图13反映了锚链工况1在不同工况下的受力曲线,从图13(a)和图13(b)可知,单独施加风荷载和流荷载的情况下,结构A的锚链受力最大,结构B受风和流荷载的影响较小。对比图13(c)、图13(d)和图13(e)可知,结构B的锚链受力对波浪荷载最为敏感,波浪和风荷载的耦合作用与单独波浪荷载作用的影响效果相差不大,而波浪和流荷载的耦合作用会降低波浪荷载对锚链受力的影响,出现这样的结果可能是因流速会减小波高增加波长的缘故。由图13(c)、图13(d)、图13(e)和图13(f)可以看出,结构C的锚链受力曲线最为稳定,锚链受力最小且锚链受力差值最小,结构C在海上环境下耐波性更好。

|
图 13 锚链在不同工况下的受力曲线图 Fig. 13 The force curve diagram of the cable under different working conditions |
本文对3种不同结构的FPV阵列系统在不同工况下4个自由度的运动响应和端部锚链受力曲线进行了研究,比较分析了不同荷载对结构稳定性和受力的影响情况,得出如下结论:
1)单独考虑运动响应来说,结构A对风荷载较为敏感,更适合安装在风荷载较小的水平面,结构B和结构C可放置在波浪较大的区域;
2)单独考虑锚固锚链的受力情况可得出,结构A的锚链受力最大,且主要受风荷载的影响较大,结构C的锚链受力最小也最为稳定;
3)本文的研究结果对新型FPV结构设计提供了设计依据,可根据现实环境荷载设计相应的模型结构。
| [1] |
耿娜. 太阳能光伏发电现状与发展前景分析[J]. 现代经济信息, 2018(17): 368. DOI:10.3969/j.issn.1001-828X.2018.25.312 |
| [2] |
陈静, 郑维娟. 中国太阳能光伏发电的发展现状及前景[J]. 时代农机, 2018, 45(3): 48–49.
|
| [3] |
MV A, SC A, AVA B, et al. Solar photovoltaic Tree: urban PV power plants to increase power to land occupancy ratio[J]. Renewable Energy, 2022.
|
| [4] |
PINTO S, STOKKERMANS J. Assessment of the potential of different floating solar technologies—overview and analysis of different case studies[J]. Energy Conversion and Management, 2020, 211.
|
| [5] |
PEREZ M, PEREZ R, FERGUSON C R, et al. Deploying effectively dispatchable floating PV on reservoirs: comparing floating PV to other renewable technologies[J]. Solar Energy, 2018, 174: 837-847. DOI:10.1016/j.solener.2018.08.088 |
| [6] |
AB A, AW A, MW B, et al. Issues, challenges, and current lacunas in design, and installation of ground mounted solar PV module mounting structure (MMS)[J]. 2022.
|
| [7] |
高亮, 窦珍珍, 白桦, 等. 光伏组件风荷载影响因素分析[J]. 太阳能学报, 2016, 37(8): 1931-1937. DOI:10.3969/j.issn.0254-0096.2016.08.005 |
| [8] |
DS A, ME A, KA A, et al. Parameters optimization of solar PV cell/module using genetic algorithm based on non-uniform mutation[J]. Computational Intelligence in Electrical Engineering, 2021.
|
| [9] |
LI Z, JI J, YUAN W, et al. Experimental & numerical investigation and optimization on a novel flat-plate PV/T system using CdfTe thin-film solar modules of sandwich structure[J]. Solar Energy, 2021, 223: 261-277. DOI:10.1016/j.solener.2021.02.009 |
| [10] |
朱绍宇, 张世富, 张冬梅, 等. 基于AQWA对一种小型浮动平台的动态响应研究[J]. 化工机械, 2021, 48(6): 888-895. DOI:10.3969/j.issn.0254-6094.2021.06.018 |
| [11] |
王江云, 李雅琴, 姜龙俊, 等. 双进气道旋风分离器内不同粒径颗粒流动特性[J]. 化工机械, 2018, 45(2): 225-231. DOI:10.3969/j.issn.0254-6094.2018.02.024 |
| [12] |
丁勤卫, 李春, 袁伟斌, 等. 风波耦合作用下垂荡板对漂浮式风力机Spar平台动态响应影响[J]. 中国电机工程学报, 2019, 39(4): 1113-1127. DOI:10.13334/j.0258-8013.pcsee.180658 |
| [13] |
岳敏楠, 王博, 李春, 等. 阵列式平台漂浮式风电场Spar平台动态响应及稳定性改进研究[J]. 振动与冲击, 2021, 40(3): 263-278. DOI:10.13465/j.cnki.jvs.2021.03.035 |
 2023, Vol. 45
2023, Vol. 45
