近些年来,开发极地资源的需求越来越大。针对极地环境与工作条件,对极地冰区海洋结构物所受冰载荷的研究也越来越深入。因此,准确模拟与预报冰区海洋结构物破冰载荷,对极地海洋结构物的设计以及航行安全保障具有重要意义。
有限元法是研究结构物与冰碰撞的常用方法,通过构建有限元模型来模拟碰撞过程,得到层冰的破坏变形方式与冰载荷等结果,但此种方法会导致碰撞区域的层冰失效删除,不符合实际碰撞后海冰的断裂与堆积现象。另外,层冰的失效删除会导致碰撞前后的模型质量不守恒,使模拟结果不够准确。为了更真实地模拟冰与结构物相互作用现象,GURTNER等[1-3]提出了粘聚单元法(CEM)。目前,国内外已有较多学者利用粘聚单元法来研究海洋结构物与海冰的碰撞过程。Statoilhydro等[4]和Bjerks[5]利用粘聚单元法模拟了灯塔与冰的相互作用,通过模拟数据与实测数据的比较,改进粘聚单元模型,证明了该方法的适用性。Feng等[6]利用粘聚单元法建立了有限元模型来模拟冰与结构物的相互作用,研究了模型的稳定性,并进行了参数敏感性分析,更好地了解粘聚单元材料参数对模拟结果的影响。Pang等[7]通过粘聚单元法模拟发现四面体冰单元网格由于具有对角线路径,可以更真实地模拟裂纹的扩展。王峰[8-9]建立了海洋结构物与平整冰碰撞的有限元模型,采用粘聚单元模型研究海冰的弯曲断裂破坏模式以及结构物所受冰载荷,通过与模型实验结果对比,对数值模拟进行了验证。蒋昱妍[10]在粘聚单元法中采用2种浮力简化模型,进行了不同冰厚下的柱状结构物-层冰碰撞的数值模拟以及碰撞力的详细分析。詹开宇等[11]使用粘聚单元法建立层冰的数值模型,进行了层冰与锥形立柱相互作用的数值模拟,研究了不同抗冰锥角、不同冰厚等参数对立柱所受冰载荷的影响,发现模拟结果与实测和试验结果吻合良好。黄其[12]基于试验冰况和实验数据,验证了粘聚单元法模拟破冰船-层冰碰撞的可靠性。卢腾超等[13]基于粘聚单元法研究发现初始缺陷对于平整冰的断裂破坏模式和冰载荷均有重要影响。
本文基于粘聚单元法,构建层冰与半潜式海洋平台碰撞的有限元模型,并将通过数值模拟计算得到的冰力值与经验公式计算得到的冰力值进行对比,验证粘聚单元法在模拟海洋结构物与层冰碰撞过程的准确性;同时分析碰撞区域平台立柱各构件吸能变化。在此基础上,研究粘聚单元不同断裂能量释放率、不同牵引力-位移准则(TSL)曲线形式对冰力的影响。
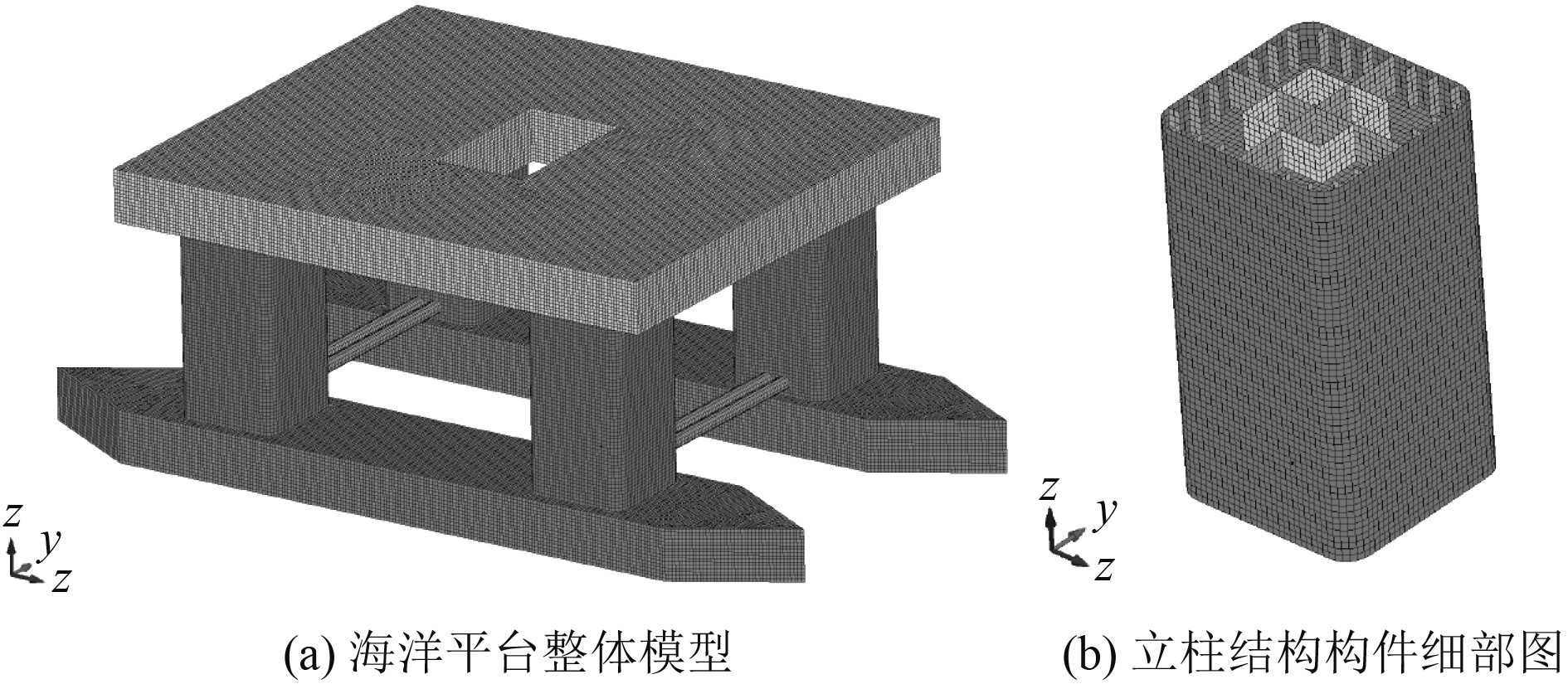
1 有限元模型的构建 1.1 半潜式海洋平台有限元模型采用有限元软件Ls-dyna进行层冰-半潜式海洋平台碰撞的数值模拟研究。数值模拟构建典型的半潜式海洋平台模型,模型参考相关文献[14],主要由甲板、立柱、横撑、浮箱4部分结构构成,各结构尺寸参数见表1。平台网格划分采用尺寸0.5 m×0.5 m的正方形壳单元网格,材料采用Ls-dyna中的*MAT-003 PLASTIC-KINEMATIC,材料参数见表2。考虑到实际情况,碰撞位置在平台作业吃水线平面处,层冰与平台某一立柱发生碰撞。半潜式海洋平台整体结构及立柱细部结构有限元模型如图1所示。
|
|
表 1 半潜式海洋平台各结构尺寸 Tab.1 Structural dimensions of semi submersible offshore platform |
|
|
表 2 平台材料参数 Tab.2 Platform material parameters |
|
图 1 半潜式海洋平台有限元模型 Fig. 1 Finite element model of semi-submersible offshore platform |
粘聚单元法是在有限元法的基础上发展起来的。层冰模型由冰体单元与粘聚单元共同构成,离散的冰体单元通过沿着内部边界插入极薄的粘聚单元相互连接。在与结构物碰撞时,冰体单元因外部应力而发生位移并通过共享节点将应力传递给粘聚单元,使粘聚单元发生位移。粘聚单元在达到位移最大分离值时失效并被删除,使相连的冰体单元脱落形成碎冰并堆积。因粘聚单元极薄,体积较小,质量相对于冰体单元可以忽略不计,因此,层冰质量在碰撞前后几乎不变。由此可见,与有限元法(FEM)、扩展有限元法(XFEM)和离散元法(DEM)等数值方法相比,粘聚单元法(CEM)不仅满足守恒定律,在模拟冰断裂破碎堆积过程方面也具有优势。
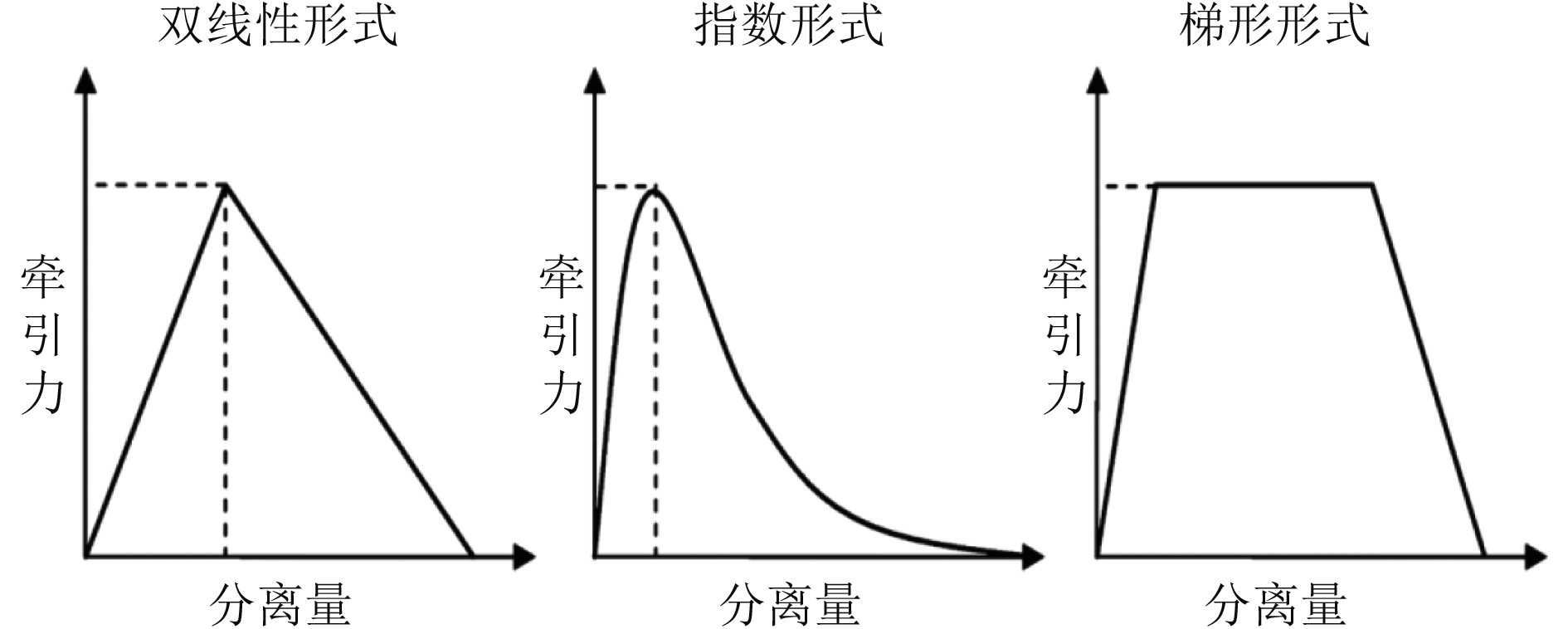
粘聚单元的破坏准则遵循牵引力—位移准则(TSL)曲线,该曲线表示粘聚单元在失效断裂时所受的牵引力和分离位移之间的关系,主要有3种形式线性软化模型、指数软化模型以及梯形软化模型。各曲线形式如图2所示,曲线与坐标轴围成的面积表示粘聚单元失效所需的能量,即断裂能量释放率。
|
图 2 牵引力-位移准则曲线 Fig. 2 Traction-separation law curve |
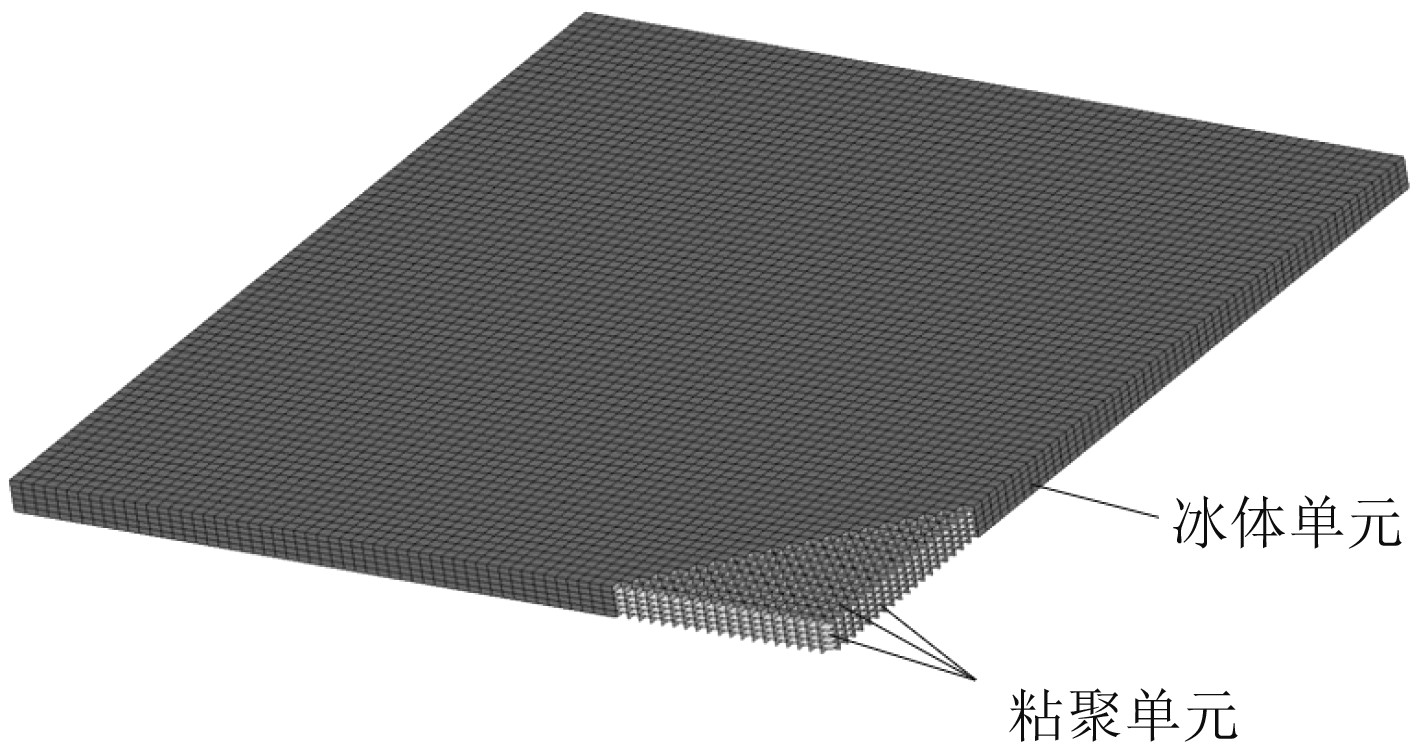
本文模拟的层冰尺寸为30 m×30 m×1 m。将粘聚单元插入冰体单元内部,两者均采用8节点6面体单元结合组成层冰模型。将冰体单元网格尺寸划分为0.4 m×0.4 m×0.2 m,粘聚单元为极薄体单元,厚度为10−4 m。冰体单元与粘聚单元模型如图3所示。
|
图 3 冰体单元与粘聚单元有限元模型 Fig. 3 Ice element and cohesive element finite element models |
冰体单元采用DYNA中分段线性弹塑性材料*MAT-024 PIECEWISE-LINEAR-PLASTIC,其Cowper-Symonds本构模型能够较好地表示材料等效应力随应变率与应变变化的关系,表达式为:
| $ {\sigma _r} = \left[1 + {\left(\frac{{\mathop \varepsilon \limits^ \cdot }}{C}\right)^{1/P}}\right]\left[{\sigma _0} + {f_h}\left(\varepsilon _{eff}^{Pla}\right)\right]。$ | (1) |
式中:
粘聚单元采用*MAT-186 COHESIVE-GENERAL,其TSL曲线采用梯形形式。冰材料与粘聚单元材料相关参数设置见表3。梯形形式TSL曲线面积表达式为:
|
|
表 3 冰体单元及粘聚单元材料参数 Tab.3 Parameters of ice materials and cohesive element materials |
| $ {G}_{I}^{c}=\frac{1}{2}{T}_{I}^{\mathrm{max}}(\left|{\lambda }_{2}-{\lambda }_{1}\right|+{u}_{I}^{c})。$ | (2) |
式中:
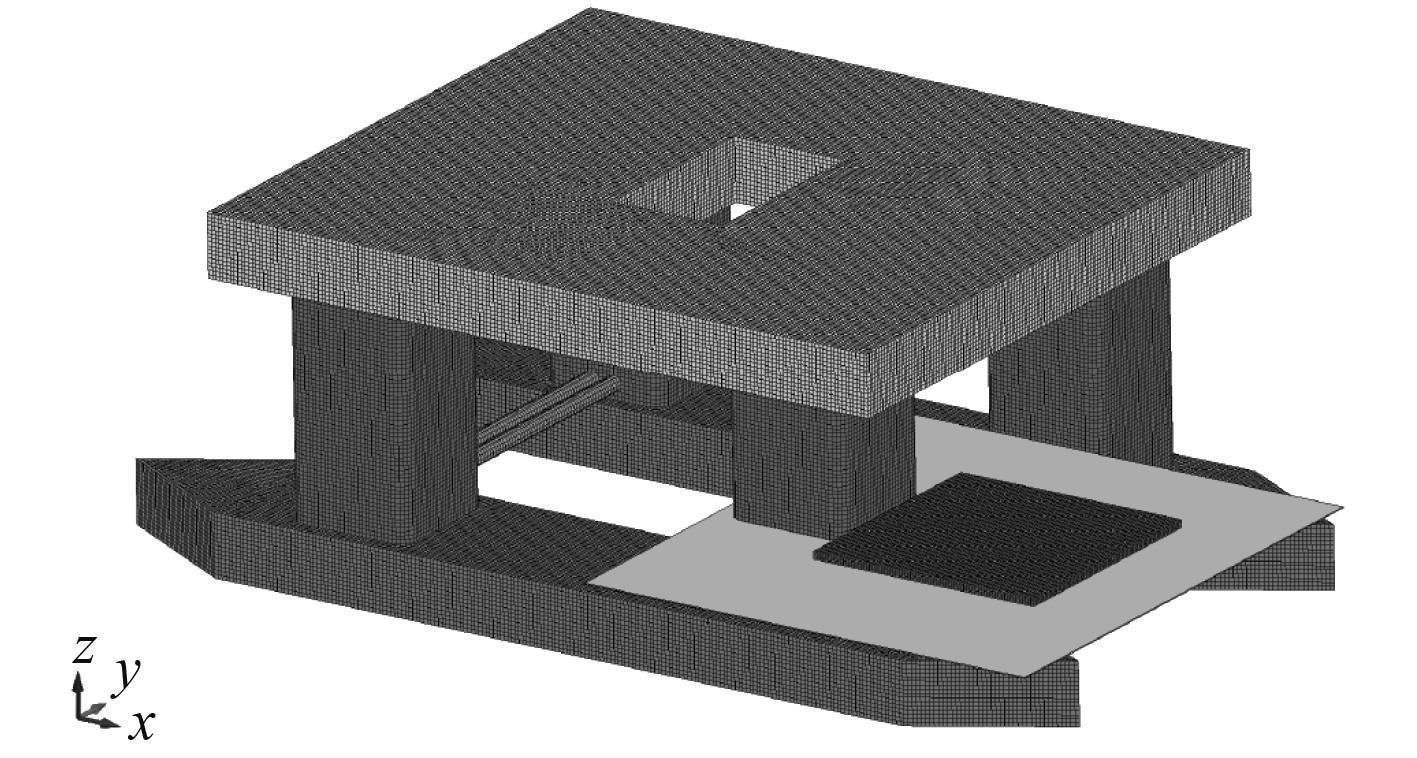
为接近真实现象,对整个模型施加重力,在层冰底部放置一块约束四边的刚性板来模拟流的影响,刚性板可为层冰提供支撑力,模拟海水浮力的影响。设置层冰以0.4 m/s的恒定速度撞击平台立柱,数值模拟时间设为5 s。层冰与半潜式海洋平台碰撞的有限元模型如图4所示。
|
图 4 层冰与半潜式平台碰撞有限元模型 Fig. 4 Finite element model of collision between layer ice and semi-submersible platform |
目前,国内外挤压冰力经验公式形式较多。参考相关文献[15],采用加拿大灯塔规范公式与数值模拟计算的冰力进行对比。公式如下:
| $ F = mDh{\sigma _c} 。$ | (3) |
式中:
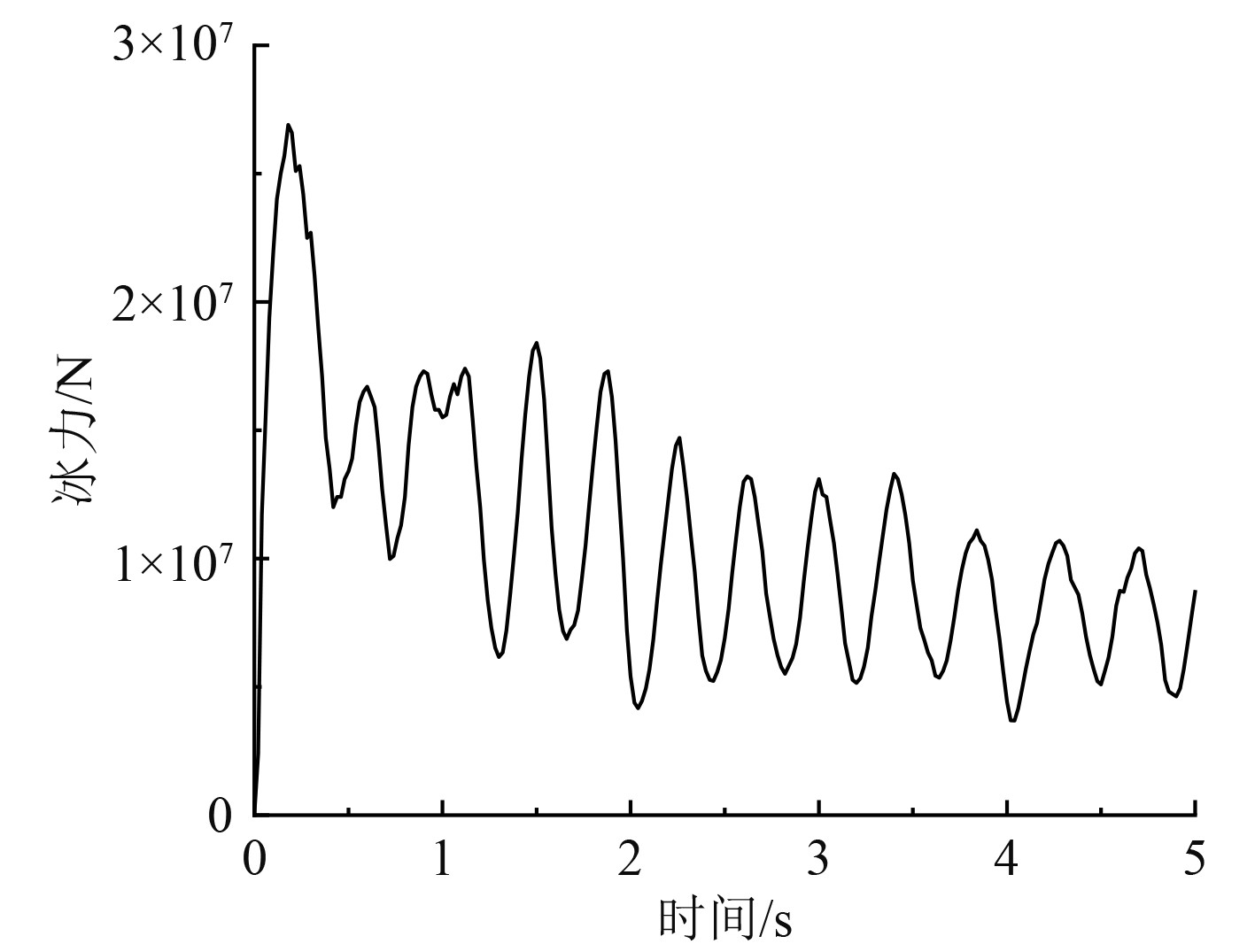
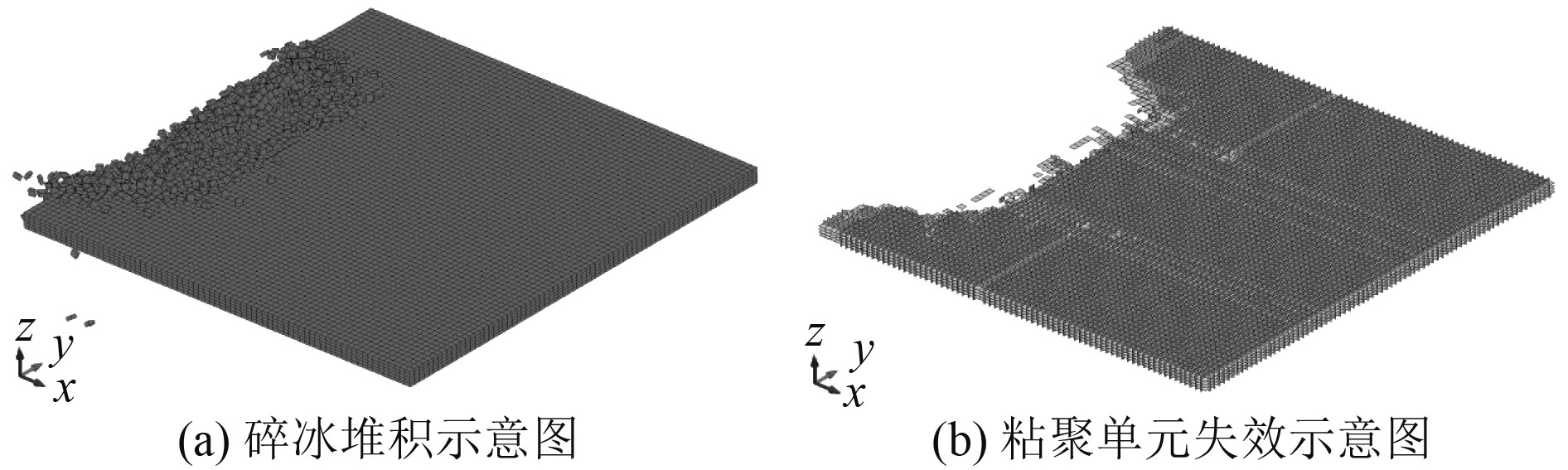
数值模拟得到的冰力时历曲线如图5所示,数值模拟的碎冰堆积及粘聚单元失效如图6所示。
|
图 5 数值模拟冰力值时历曲线 Fig. 5 Time history curve of numerical simulation of ice force value |
|
图 6 t=5 s时层冰模型变形示意图 Fig. 6 Deformation diagram of layer ice model at t=5 s |
由图5可知,由于立柱较宽,碰撞面积较大且在层冰与立柱接触时就达到了最大,因此一开始冰力就达到了峰值。由于碰撞产生的应力传递到层冰内部,导致粘聚单元失效,冰体单元脱落形成碎冰并发生堆积,挤压立柱,因此层冰主要发生局部挤压破坏。由于碰撞速度恒定,层冰挤压在整个碰撞过程中一直进行,导致冰力减小并逐步趋于稳定波动状态。由图6可知,碎冰堆积在碰撞区域,粘聚单元在碰撞区域失效也最为严重,并且应力的传递使非碰撞区域的粘聚单元也发生部分失效,形成裂纹。
将相应参数代入式(3)计算,可得数值模拟的冰力均值为10.77 MN,采用规范公式计算的冰力值为11.01 MN,二者偏差为2.2%,较为接近,说明通过粘聚单元法进行数值模拟计算的结果可信。
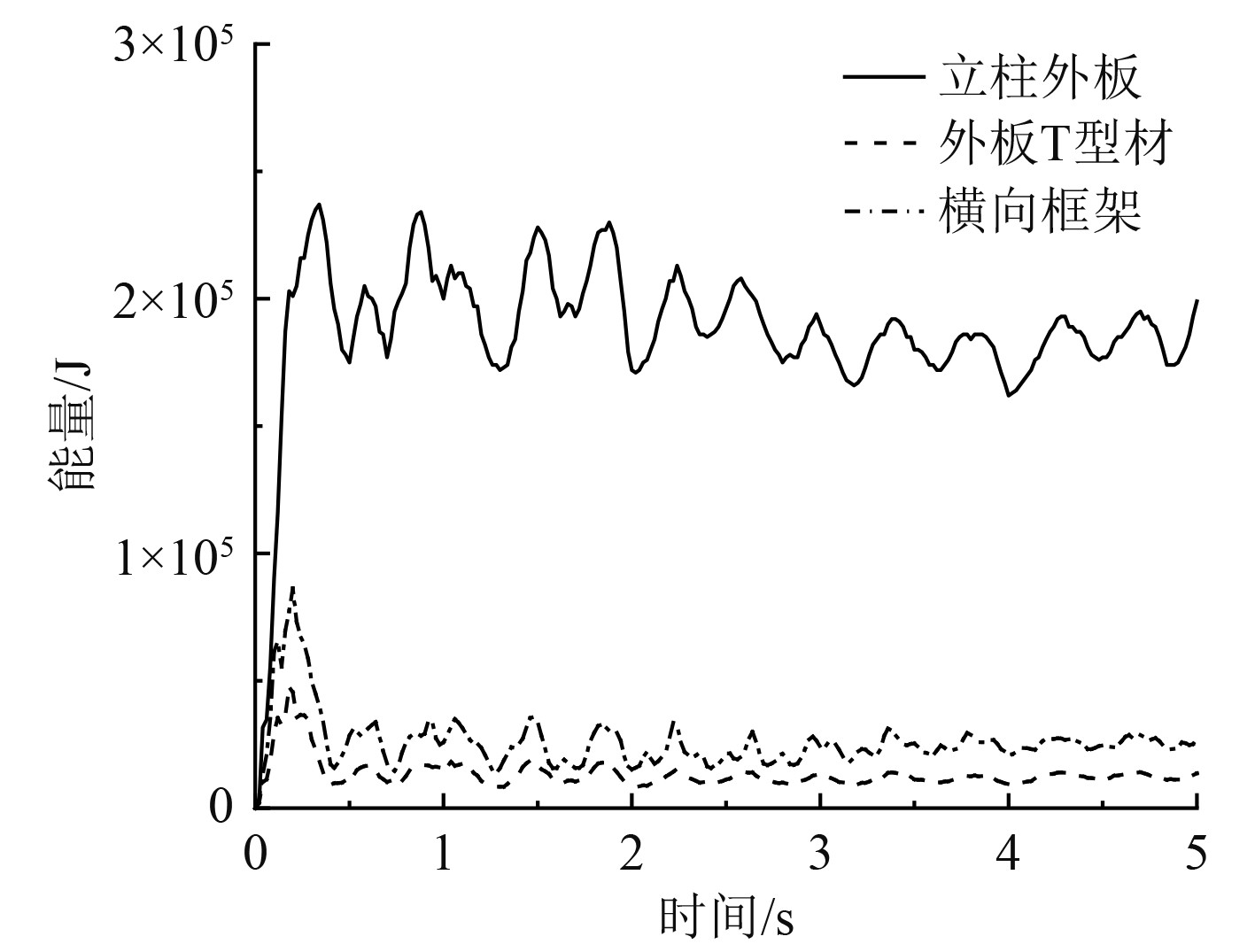
2.3 结构吸能分析数值模拟得到的碰撞过程中立柱各构件能量变化如图7所示。
|
图 7 数值模拟计算的立柱各构件吸能变化 Fig. 7 Energy absorption change of each component of the column calculated by numerical simulation |
可以看出,层冰与平台立柱碰撞过程中,立柱各构件内能均增大至趋于稳定波动状态。其中,立柱外板吸能最大且远大于其他构件,均值为1.87×105 J。占比82.67%,横向框架次之,均值为2.59×104 J,外板T型材吸能最小,均值为1.33×104 J,说明在层冰与海洋平台的碰撞过程中,平台立柱结构是主要的耗能部分,且外板是立柱结构的主要耗能构件。
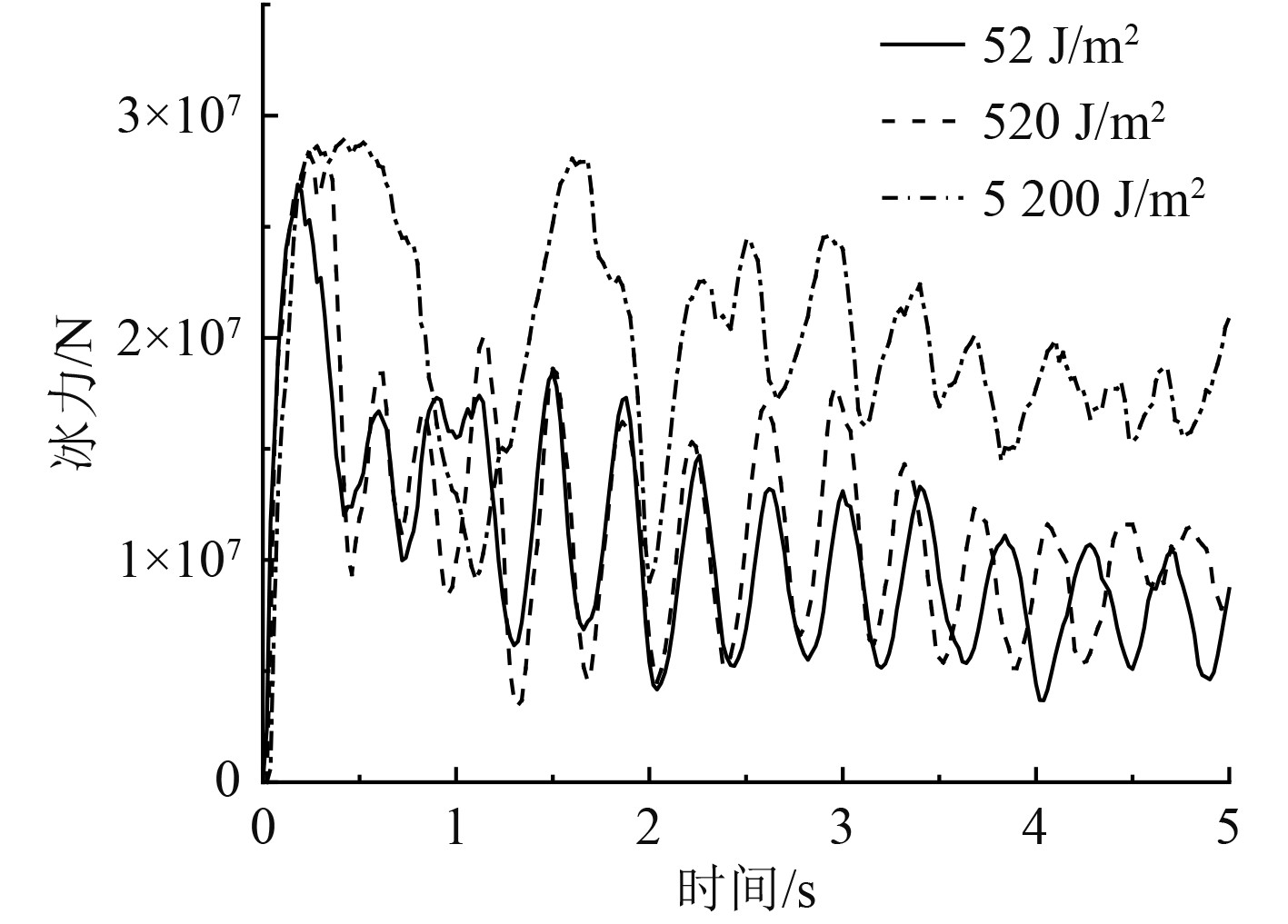
3 粘聚单元参数敏感性分析 3.1 不同断裂能量释放率的冰力对比基于文献[8]可知,一年冰与多年冰的断裂能量释放率存在差异。从式(2)可以看出,当TSL曲线类型确定时,最大牵引力、失效位移与断裂能量释放率之间相互关联:最大牵引力保持一致时,改变断裂能实际上是改变了粘聚单元的失效位移。保持其余设置一致,计算并对比52 J/m2、520 J/m2、5200 J/m2各断裂能的冰力,研究断裂能量释放率对冰力的影响。数值模拟得到的各断裂能的冰力时历曲线见图8,对比结果见表4。
|
图 8 不同断裂能量释放率的冰力时历曲线 Fig. 8 Time history curves of ice force with different fracture energy release rates |
|
|
表 4 不同断裂能量释放率的冰力对比 Tab.4 Comparison of ice force with different fracture energy release rates |
由计算结果可知,冰力均值、峰值均随着断裂能量释放率的增大而增大。这是因为受到挤压时,断裂能越大的粘聚单元越不容易失效,此时被粘聚单元包围的冰体单元难以脱落。断裂能较大的粘聚单元失效后,形成碎冰的冰体单元变形较大,冰力也随之增大。粘聚单元的断裂能会影响冰体单元的相互作用,断裂能低的粘聚单元会变得极易破坏失效。因此,在数值模拟中适当增加断裂能量释放率很有必要。
3.2 不同形式TSL曲线下的冰力对比TSL曲线作为粘聚单元的本构关系式,研究其不同形式对数值结果的影响很有必要。将各曲线与横坐标围成的面积调整至相同,以保证断裂能大小一致。保持其余设置一致,通过数值模拟研究不同TSL曲线形式对冰力的影响。数值模拟得到的各曲线冰力时历曲线见图9,对比结果见表5。

|
图 9 不同TSL曲线形式的冰力时历曲线 Fig. 9 Time history curves of Ice force with different TSL curve forms |
|
|
表 5 不同TSL曲线形式的冰力对比 Tab.5 Comparison of ice force with different TSL curve forms |
由计算结果可知,3条TSL软化曲线得到的冰力时历曲线波动频率趋势较为吻合,冰力均值与标准差也较为接近,差异较小。不同曲线形式下的均值及标准差最大偏差分别为7.7%与12.1%,线性形式曲线得到的均值略大于其余2条曲线。总的来说,当断裂能取值合适,不同形式的TSL曲线对冰力的影响相当有限,这与相关文献[16]的研究结果吻合。
4 结 语1)对比数值模拟与经验公式计算得到的冰力值,发现两者偏差仅为2.2%,较为接近,验证了采用粘聚单元法进行数值模拟计算的准确性。数值模拟发现粘聚单元法可较好地模拟层冰与海洋结构物的碰撞过程、层冰裂纹的形成与展开以及碎冰的堆积过程,同时研究发现层冰破坏模式主要是局部挤压破坏。
2)通过数值模拟得到碰撞区域立柱各构件吸能变化情况,发现外板吸能最大,占比82.67%,外板T型材次之,横向框架最小,说明立柱外板是层冰-海洋平台碰撞过程中主要的受力耗能构件。
3)通过研究粘聚单元参数对冰力的影响可发现,一定范围内,在保持其他参数一致的情况下,冰力值随着断裂能量释放率的增大而增大,但不同形式的TSL曲线对数值计算的冰力值带来的影响十分有限。
| [1] |
GÜRTNER A. Experimental and numerical investigations of ice-Structure interaction[J]. Norges teknisk-naturvitenskapelige universitet, Fakultet for ingeniø rvitenskap og teknologi, Institutt for bygg, anlegg og transport, 2009, 13(2): 21-30. |
| [2] |
GÜRTNER A, BJERKS M, FORSBER J, et al. Numerical modelling of a full scale ice event[C]// 20th IAHR International Symposium on Ice. 2010: 48–60.
|
| [3] |
KOUNK I, YU S. A cohesive element framework for dynamic ice-structure interaction problems: part III—case studies[C]// Asme International Conference on Ocean, 2010: 801–809.
|
| [4] |
STATOILHYDRO A G, BJERKS M, W KÜHNLEUN, et al. Numerical simulation of ice action to a lighthouse[J]. American Society of Mechanical Engineers, 2009, 23(11): 77-86. |
| [5] |
BJERKÅS, MORTEN, ALBREKTSEN A, et al. Static and dynamic ice actions in the light of new design codes[C]// Asme International Conference on Ocean. American Society of Mechanical Engineers, 2010: 12–19.
|
| [6] |
FENG D, PANG S D, ZHANG J. Polar and arctic sciences and technology; petroleum technology - parameter sensitivity in numerical modelling of I[J]. ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering - Busan, South Korea, 2016(8): V008T07A012.
|
| [7] |
PANG S D, ZHANG J, POH L H, et al. The modelling of ice-structure interaction with cohesive element method: limitations and challenges[C]//International Conference on Port & Ocean Engineering Under Arctic Conditions, 2015: 24–34.
|
| [8] |
王峰. 基于粘聚单元模型的海洋结构物与平整冰相互作用数值研究[D]. 上海: 上海交通大学, 2019.
|
| [9] |
王峰, 邹早建, 任奕舟. 基于粘聚单元模型的平整冰-竖直圆柱体碰撞数值模拟[J]. 振动与冲击, 2019, 38(16): 153-158. |
| [10] |
蒋昱妍. 基于粘聚单元法的海洋结构物-层冰碰撞数值模拟[D]. 大连: 大连理工大学, 2020.
|
| [11] |
詹开宇, 曹留帅, 万德成. 基于黏聚单元法计算分析海洋平台锥形立柱冰载荷[J]. 海洋工程, 2021, 39(4): 62-69. |
| [12] |
黄其. 基于内聚力单元法的海洋结构物冰载荷模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [13] |
卢腾超, 邹早建, 王阳, 等. 考虑初始缺陷的平整冰-锥体结构碰撞数值模拟[J]. 振动与冲击, 2021, 40(6): 250-256. |
| [14] |
董科, 李友龙. 半潜式海洋平台受浮冰撞击作用损伤分析[J]. 舰船科学技术, 2018, 40(1): 57-61. DONG K, LI Y L. Damage analysis of a semi-submersible offshore platform bump by floating ice[J]. Ship Science and Technology, 2018, 40(1): 57-61. |
| [15] |
董庆峰. 大尺度海洋结构上的冰力识别研究[D]. 青岛: 中国石油大学, 2006.
|
| [16] |
CORNEC A, SCHEIDER I, SCHWALBE K H. On the practical application of the cohesive model[J]. Engineering fracture mechanics, 2003, 70(14): 1963-1987. DOI:10.1016/S0013-7944(03)00134-6 |
 2023, Vol. 45
2023, Vol. 45
