随着人类开发海洋活动范围的不断扩大,工业装备在改造海洋过程中产生的噪声污染日益受到广泛关注。加大水下装备噪声治理,对海洋水体环境和生态系统的健康发展具有重要意义[1]。
在水下装备噪声治理方面,气泡幕发生装置可在海水中形成含有大量尺寸不同气泡的气幕,对水下噪声具有很强的衰减和屏蔽作用[2],被广泛应用于水系疏浚[3]、水下钻孔爆破[4]、声学驱鱼隔离[5]等领域的声学控制。
气泡幕中的气泡形态对声学控制效果影响显著[6]。当气泡受激共振时,其散射截面是其几何截面的1000倍以上,对于气泡群这样的多体强散射体,其气液体积浓度大于10−7时,气泡间的多次散射不可忽略[7]。几十年来,许多学者对此问题进行过大量的深入分析,并得出多体多次散射会导致气泡群阻尼系数大幅增大的结论[8]。同时气泡幕中气泡声阻尼的实验结果也表明,单个理想气泡的声阻尼远小于气泡幕中的每个气泡的平均声阻尼,气泡群的多体多次散射是增大气泡群声衰减量的主要原因[9]。
在实际情况下,气泡幕中气泡的尺寸及分布规律对声阻尼及衰减特性有显著影响[10]。为了能够得到预设的气泡尺寸及分布规律,需要对气泡幕发生装置进行优化设计。本文在分析气泡幕尺寸分布对声衰减影响规律的基础上,开展气泡幕发生装置开孔规律理论分析,通过仿真和试验验证的方式比较均匀分布和变孔距定孔径分布方案的量化效果。
1 气泡幕声衰减模型对声传播的影响 1.1 气泡谱分布特性分析气泡幕发生装置产生的气泡分布可分为对称分布(正态)和不对称分布2种。Davids等[11],Fox等[12]和Laird等[13]所做的气泡实验测量结果表明,水中气泡群分布函数倾向于后者,即不对称分布,并且基本符合Poisson分布。
在Poisson分布的情况下,气泡的分布函数
| $ n\left( R \right) = {N_0}{R^E}{e^{ - \frac{{ER}}{{{R_0}}}}} \text{,} $ | (1) |
| $ {N_0} = \frac{{{\tau _N}}}{{\displaystyle\int_0^\infty {\frac{4}{3}{\text{π}} {R^{3 + E}}{e^{ - ER/{R_0}}}dR} }} 。$ | (2) |
式中:R0、E为分布常数,R0是气泡在Poisson分布条件下的期望半径,E是对于其气泡期望半径的离散程度,TN为气泡群的体积浓度。
1.2 气泡幕声学性能分析应用气泡振动方程可推导出气泡幕的反射系数为:
| $ IR = \frac{{\left( {1 - k_1^2} \right)({e^{ - jk^{*}d}} - {e^{jk^{*}d}})}}{{{{(1 - {k_1})}^2}{e^{ - jk^{*}d}} - {{(1 + {k_1})}^2}{e^{jk^{*}d}}}},$ | (3) |
透射系数为:
| $ \begin{split} ID = & \frac{1}{2}\left\{ \left[ {{k_1}\left( {1 - IR} \right) + (1 + IR)} \right]{e^{ - jk^{*}d}} -\right.\\ & \left. \left[ {{k_1}(1 - IR) - (1 + IR)} \right]{e^{jk^{*}d}} \right\}{e^{j{k_0}d}}。\end{split} $ | (4) |
式中:
从式(1)~式(4)可以看出,气幕反射系数
固定
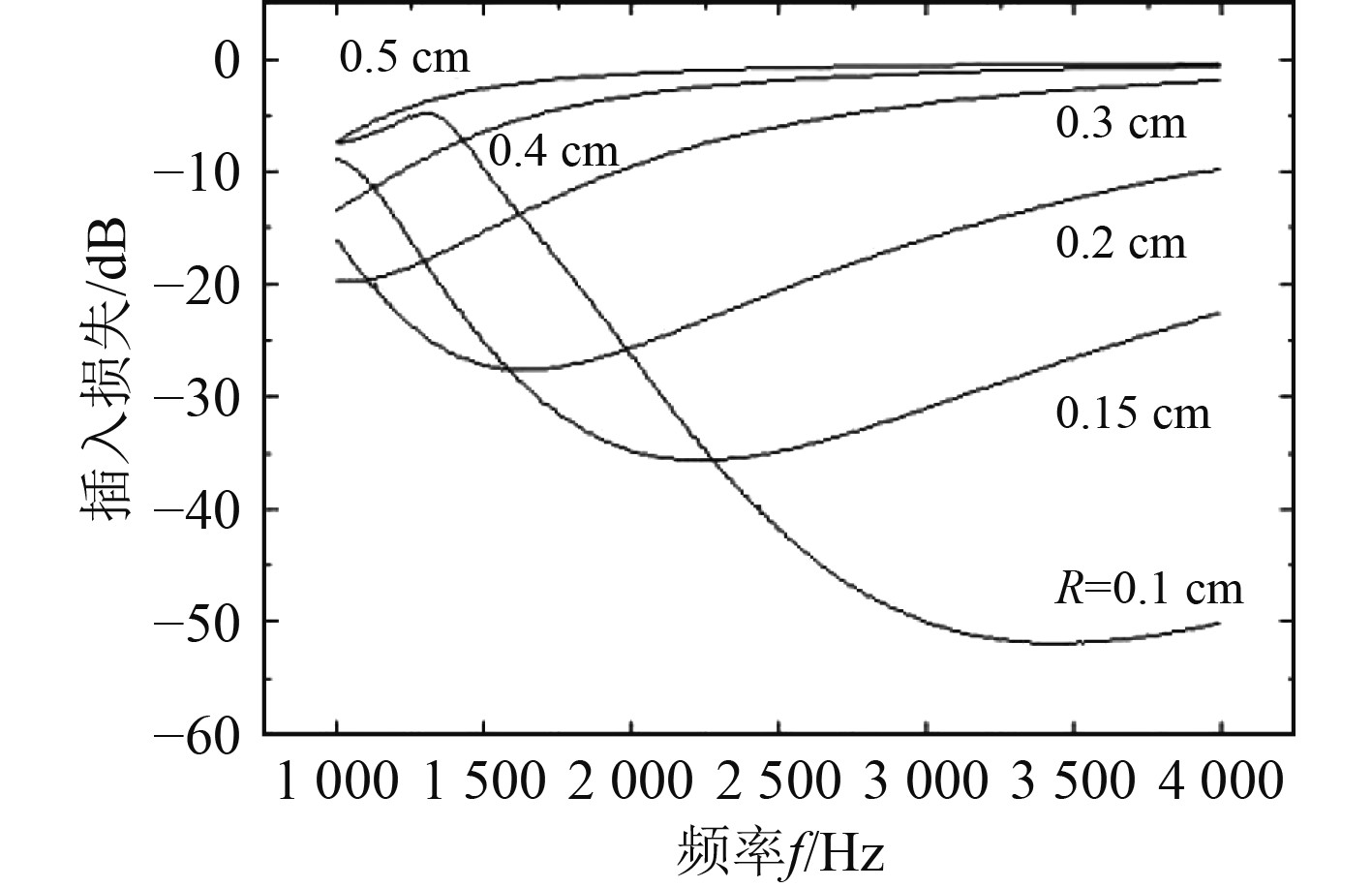
|
图 1 气泡半径变化对插入损失的影响 Fig. 1 Influence of bubble radius change on insertion loss |
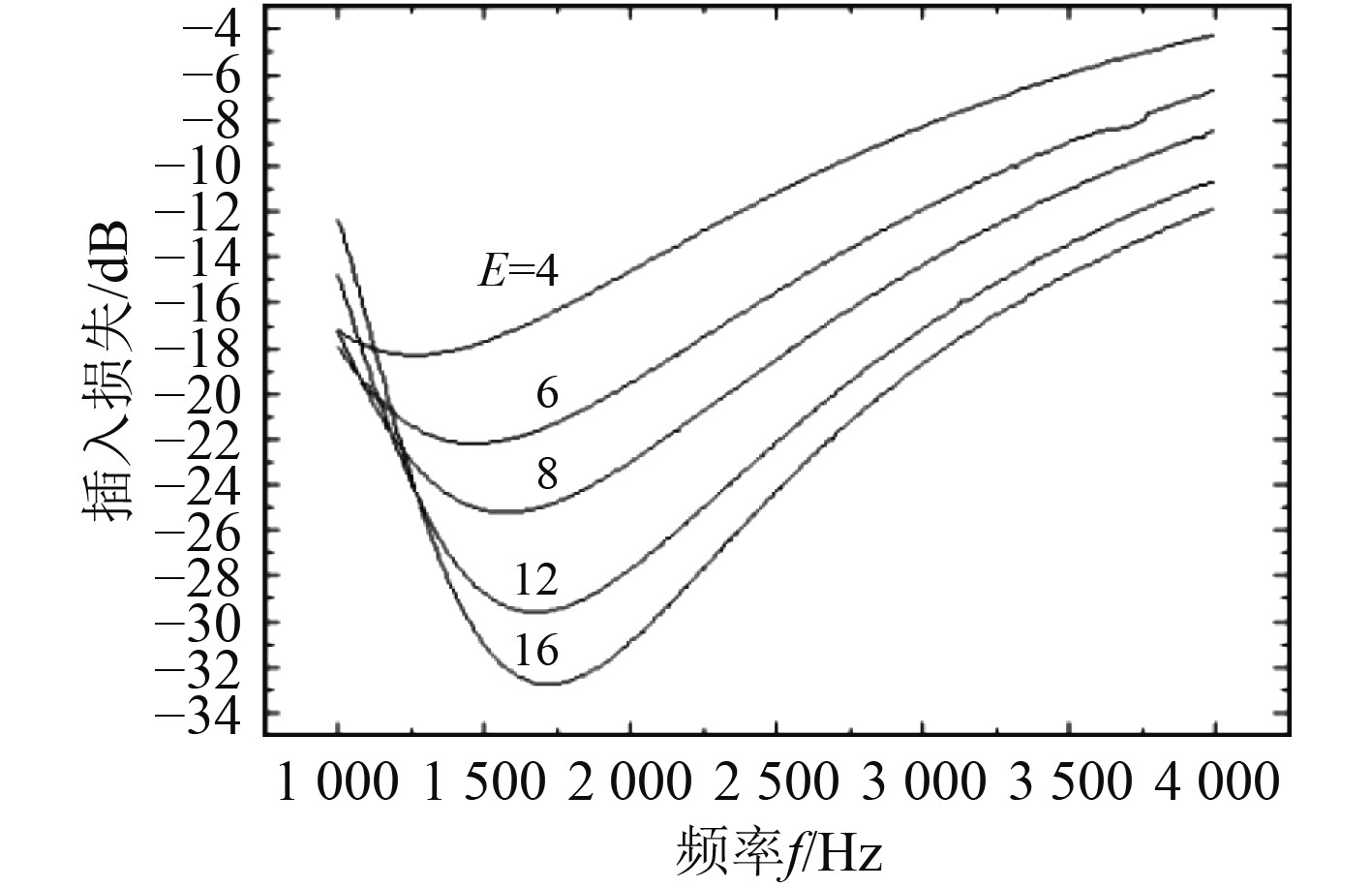
|
图 2 气泡尺度分布特性对插入损失的影响 Fig. 2 Influence of bubble size distribution characteristics on insertion loss |
可见,通过调控气泡幕中气泡尺度参数,可提高气泡幕的隔声效果。本文针对此规律,开展气泡幕发生装置的参数设计,以定孔间距变孔面积为设计原则,实现尽量均匀的气泡幕发生效果。
2 气泡幕发生装置变距定积设计 2.1 基本假设为了能够使气泡幕发生装置排气效果均匀,设计遵循的基本假设是:在单位面积上,排气量相等。以此为原则,可实现气泡发生装置排气孔的定孔间距变孔面积设计。
2.2 理论推导该原则下,各孔面积相等,孔间距不等,保证各孔流量相等。
根据基本假设,喷气装置单位面积喷气量为常数
第i行、第j列孔的喷气流速为:
| $ {v_{ij}} = \mu \sqrt {\frac{2}{{{\rho _{Hi}}}}\left( {{P_{ij}} - {P_{Hi}}} \right)}。$ | (5) |
式中:
结合理想气体状态方程:
| $ {\rho _{Hi}} = W{P_{Hi}},$ | (6) |
设各孔面积为
| $ a = \frac{{{h_{ij}}{w_{ij}}}}{{hw}} \cdot \frac{{{Q_0}}}{{{v_{ij}}}},$ | (7) |
由式(5)~式(7)有:
| $ {P_{ij}} = \left( {1 + Dh_{ij}^2w_{ij}^2} \right){P_{Hi}},$ | (8) |
其中,
由不可压缩流体伯努利方程有:
| $ {P_{i + 1,j}} + \frac{{{\rho _{i + 1,j}}V_{i + 1,j}^2}}{2} = {P_{ij}} + \frac{{{\rho _{ij}}V_{ij}^2}}{2} + \Delta {P_{ij}} 。$ | (9) |
其中:
| $ \begin{split} & {V_{ij}} = \frac{{{Q_{ij}}}}{{{A_i}}} = \frac{{\displaystyle\sum\limits_{s = 1}^i {{h_{sj}}} \cdot \displaystyle\sum\limits_{t = 1}^j {{w_{it}}} }}{{hw}} \cdot \frac{{{Q_0}}}{{{A_i}}},\\ & {V_{i + 1,j}} = \frac{{{Q_{i + 1,j}}}}{{{A_{i + 1}}}} = \frac{{\displaystyle\sum\limits_{s = 1}^{i + 1} {{h_{sj}}} \cdot \displaystyle\sum\limits_{t = 1}^j {{w_{i + 1,t}}} }}{{hw}} \cdot \frac{{{Q_0}}}{{{A_{i + 1}}}}。\end{split} $ | (10) |
其中,
沿程阻力为:
| $ \begin{split} \Delta {P_{ij}} & = \int_0^{{h_{ij}}} {\frac{\lambda }{{{d_i}}}} \cdot \frac{{{\rho _{ij}}V_{ij}^2}}{2}{\rm{d}}x = \frac{{\lambda W{P_{ij}}Q_0^2{{\left( {\displaystyle\sum\limits_{s = 1}^i {{h_{sj}}} } \right)}^2}{{\left( {\displaystyle\sum\limits_{t = 1}^j {{w_{it}}} } \right)}^2}{h_{ij}}}}{{2{d_i}A_i^2{h^2}{w^2}}}=\\ & \frac{\lambda }{{{d_i}}} \cdot \frac{{D{\mu ^2}{a^2}}}{{A_i^2}}{\left( {\sum\limits_{s = 1}^i {{h_{sj}}} } \right)^2}{\left( {\sum\limits_{t = 1}^j {{w_{it}}} } \right)^2}{h_{ij}}{P_{ij}} 。\\[-21pt] \end{split} $ | (11) |
式中:
将式(8)、式(10)、式(11)代入式(9),可得:
| $ \begin{split} &{P_{H,i + 1}}\left( {1 + Dh_{i + 1,j}^2w_{i + 1,j}^2} \right)\left[ 1 + \frac{{D{\mu ^2}{a^2}}}{{A_{i + 1}^2}}{{\left( {\sum\limits_{s = 1}^i {{h_{sj}} + {h_{i + 1,j}}} } \right)}^2}\times \right.\\ & \left.{{\left( {\sum\limits_{t = 1}^j {{w_{i + 1,t}}} } \right)}^2} \right] = {P_{Hi}}\left( {1 + Dh_{ij}^2w_{ij}^2}\right)\times \\ & \left[ {1 + \frac{{D{\mu ^2}{a^2}}}{{A_i^2}}{{\left( {\sum\limits_{s = 1}^i {{h_{sj}}} } \right)}^2}{{\left( {\sum\limits_{t = 1}^j {{w_{it}}} } \right)}^2}\left( {1 + \frac{\lambda }{{{d_i}}}{h_{ij}}} \right)} \right]。\\[-21pt] \end{split} $ | (12) |
此为关于
| $ \begin{split}&\scriptsize {h_{i + 1,j}} = \\ &\scriptsize\sqrt {\frac{{{P_{Hi}}}}{{{P_{H,i + 1}}}}\left( {\frac{1}{{Dw_{i + 1,j}^2}} + h_{ij}^2} \right)\frac{{1 + \frac{{D{\mu ^2}{a^2}}}{{A_i^2}}{{\left( {\displaystyle\sum\limits_{s = 1}^i {{h_{sj}}} } \right)}^2}{{\left( {\displaystyle\sum\limits_{t = 1}^j {{w_{it}}} } \right)}^2}\left( {1 + \frac{\lambda }{{{d_i}}}{h_{ij}}} \right)}}{{1 + \frac{{D{\mu ^2}{a^2}}}{{A_{i + 1}^2}}{{\left( {\displaystyle\sum\limits_{s = 1}^i {{h_{sj}} + {h_{i + 1,j}}} } \right)}^2}{{\left( {\displaystyle\sum\limits_{t = 1}^j {{w_{i + 1,t}}} } \right)}^2}}} - \frac{1}{{Dw_{i + 1,j}^2}}} 。\end{split}$ | (13) |
等号右边的
同理可得:
| $ \begin{split} & \scriptsize{w_{i,j + 1}} =\\ & { \scriptsize\sqrt {\left( {\dfrac{1}{{Dh_{i,j + 1}^2}} + w_{ij}^2} \right)\dfrac{{1 + \dfrac{{D{\mu ^2}{a^2}}}{{A_j^2}}{{\left( {\displaystyle\sum\limits_{s = 1}^i {{h_{sj}}} } \right)}^2}{{\left( {\displaystyle\sum\limits_{t = 1}^j {{w_{it}}} } \right)}^2}\left( {1 + \dfrac{\lambda }{{{d_j}}}{w_{ij}}} \right)}}{{1 + \dfrac{{D{\mu ^2}{a^2}}}{{A_{j + 1}^2}}{{\left( {\displaystyle\sum\limits_{s = 1}^i {{h_{s,j + 1}}} } \right)}^2}{{\left( {\displaystyle\sum\limits_{t = 1}^j {{w_{it}} + {w_{i,j + 1}}} } \right)}^2}}} - \dfrac{1}{{Dh_{i,j + 1}^2}}}}。\end{split} $ | (14) |
等号右边的
按照面积相近以及进气口压力相近原则,分别建立均匀分布排气孔、变距定积排气孔模式的气泡幕发生装置模型,应用有限元方法计算进气口及其最近排气孔处的压强,验证排气分散效果能否实现均匀分散、增加气液混合面积、优化气泡群分布特性的目的。
3.2 均匀分布排气孔模型建立开口扁孔半径为30 mm的排气装置模型,并对其划分有限元网格,如图3所示。节点数为78710,单元数为418379。采用两相流Mixture模型,k-ε粘度模型,进气流量4 kg/s,得到气体喷射情况如图4所示。
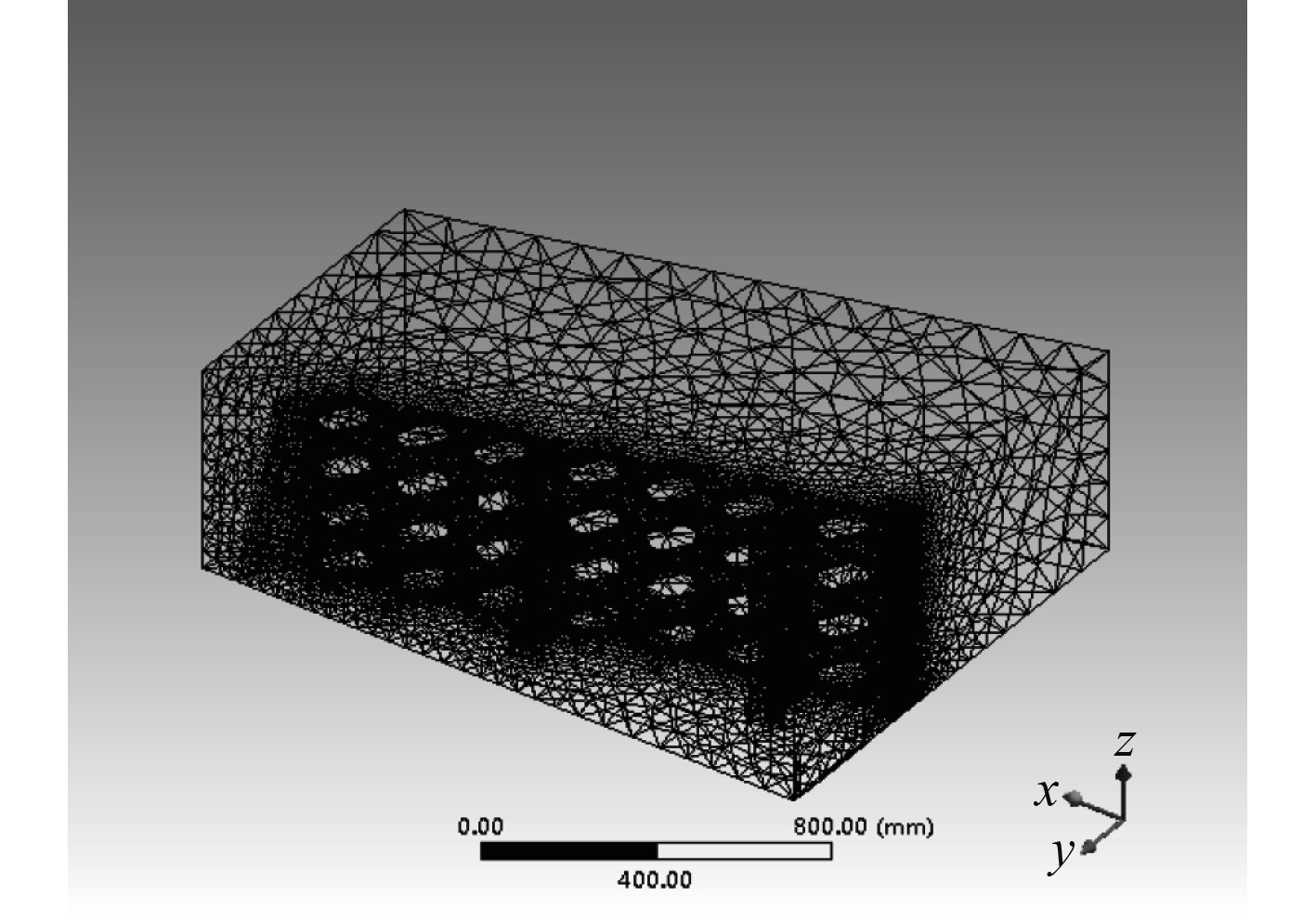
|
图 3 4 kg/s进气流速均匀分布排气孔方案网格模型 Fig. 3 Grid model of exhaust hole scheme with uniform distribution of 4 kg/s intake flow rate |

|
图 4 均匀分布排气孔模型纵向气相分布情况 Fig. 4 Longitudinal gas phase distribution of the uniformly distributed vent model |
图中,z为距装置底部距离,4 kg/s进气流速4 kg/s流速均匀分布排气孔模型中,下层喷孔与上层喷孔喷射状态非常不均匀,在下层开孔中,甚至出现倒灌情况,对气体均匀分布不利。
进气口压力为137826.45~139818.97 Pa,最近排气孔压力为135833.94~137826.45 Pa,开孔总面积为213568.13 mm2。
因为进气口压力与排气管路背压有关,为了保证优化设计不会影响排气管路背压及其他设备参数,后续变距定积4 kg/s流速分析中,以上述开孔总面积或进气初始位开孔压力为设计依据。
3.3 变距定积排气孔模型 3.3.1 开孔总面积接近原则在变距定积设计条件下,根据解析计算结果,无法得到合适的面积接近原则设计数据,故本文依据进气口压力接近原则进行验证。
3.3.2 进气初始位开孔压力接近原则根据有限元计算,均匀分布排气孔模型中,4 kg/s流速扁孔半径30 mm情况下进气初始位开孔的压力为135833.94~137826.45 Pa。以此压力为设计原则,可得到比较合理的开孔方式为开孔面积3060 mm2,上下预留110 mm,左右预留150 mm,形成9列、6行、解析计算最近排气孔压力122367.23 Pa、开孔总面积165240 mm2的开孔阵列。建立此设计排气装置模型,并对其划分有限元网格,如图5所示。
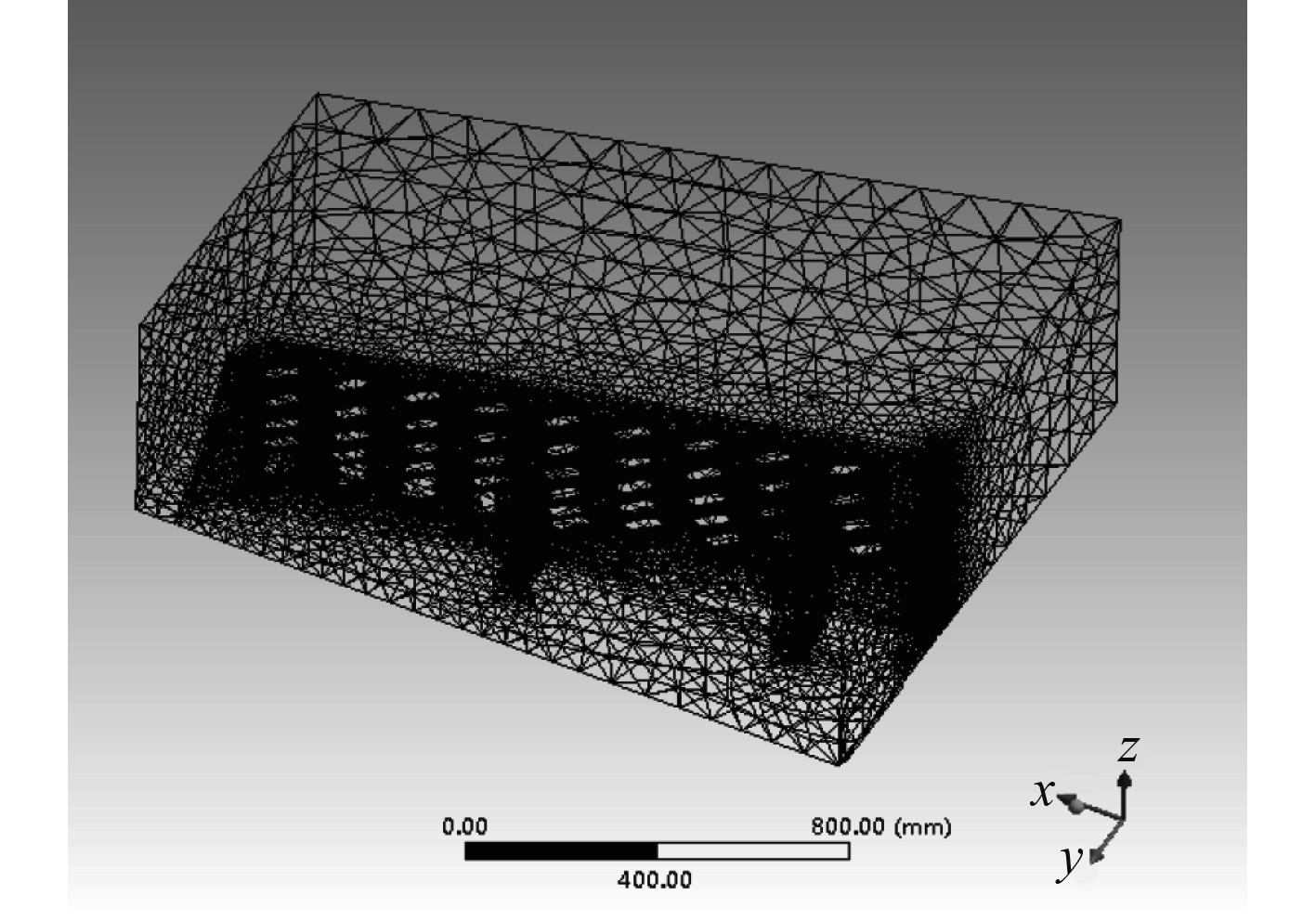
|
图 5 4 kg/s流速进气口压力接近原则变距定积方案网格模型 Fig. 5 Grid model of the variable-pitch / constant-size scheme at 4 kg/s flow rate under the principle of inlet pressure close |
节点数133682,单元数722468。采用两相流Mixture模型,k-ε粘度模型,得到气体喷射情况如图6所示。可知,相比均匀开孔排气设计方案,该设计条件下气体喷射结构更加均匀。

|
图 6 进气初始位开孔压力接近原则变距定积模型纵向气相分布情况 Fig. 6 Longitudinal gas phase distribution of the variable-pitch / constant-size model under the principle of inlet pressure close at the initial-positioning vent |
由计算可知,进气口压力为136814.59~138169.89 Pa,最近排气孔压力为136814.59~138169.89 Pa。与解析计算设计最近排气孔压力122367.23 Pa相比,两者相差约11.00%。与均匀开孔排气方案相比,进气口压力约低0.96%,最近排气孔压力高出约0.48%。
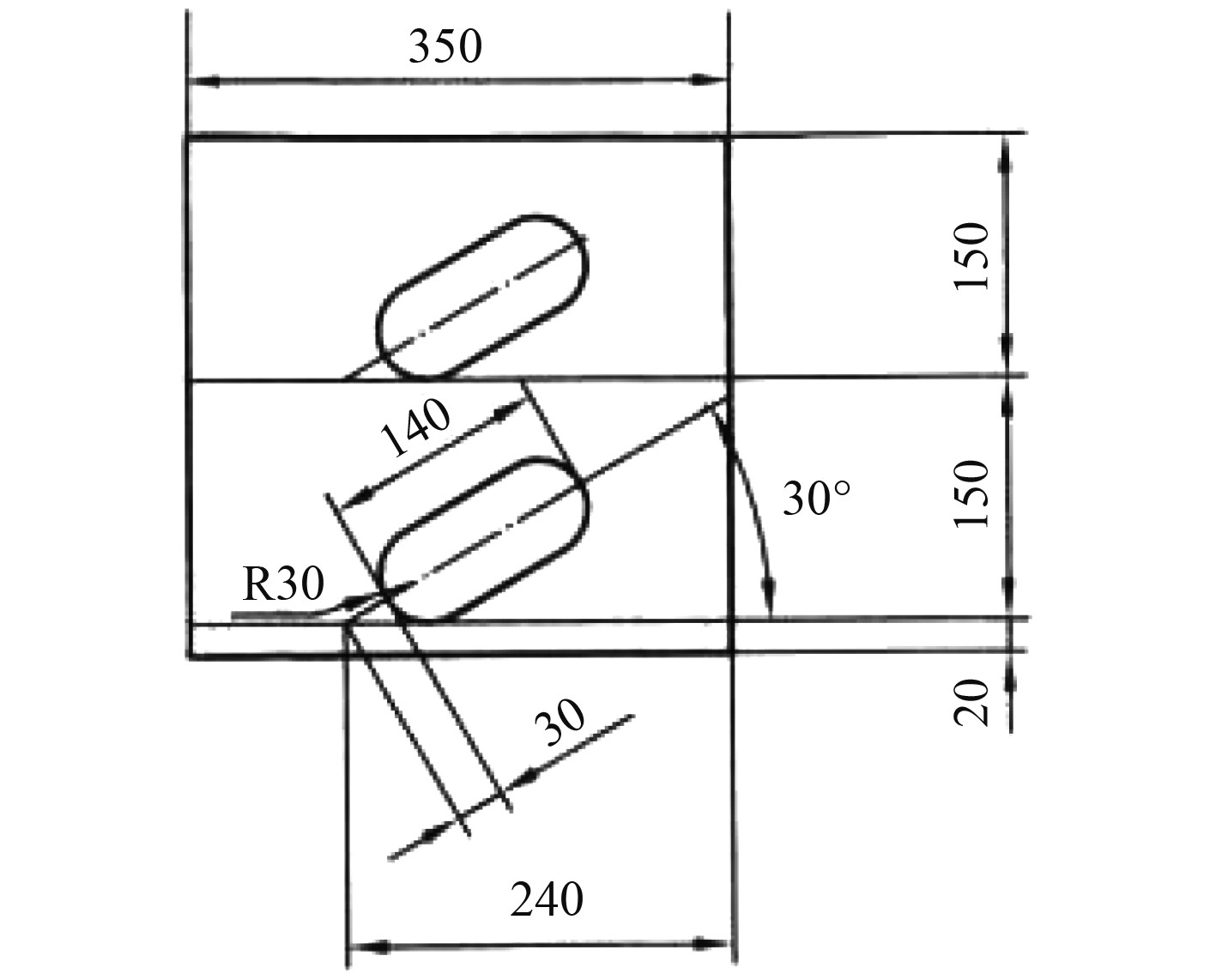
4 排气试验验证按照第3节中的参数,加工模型如图7所示。
|
图 7 均匀分布排气模型 Fig. 7 Uniformly distributed vent model |
在循环水槽中开展排气试验,观察不同模型排气状况、气泡状态。试验参数如表1所示。
|
|
表 1 试验参数 Tab.1 Test parameters |
观察两模型的排气情况,在相同排气条件下,各考察1000个气泡,均匀排气模式可见气泡平均直径约8.96 mm,中位直径约6.29 mm,方差约0.71 mm2,最下层排气孔基本未排气;变距定积排气模式可见气泡平均直径约5.25 mm,中位直径约4.36 mm,方差约0.37 mm2,最下层排气孔能与上层气孔一样基本保持均匀排气。变距定积排气模型排气效果明显优于均匀排气模型。
5 结 语本文对气泡幕发生装置开孔规律进行了理论推导和分析,通过仿真和试验验证的方式比较了不同方案的量化效果。
1)水中气泡群分布函数基本符合Poisson分布。通过调控气泡幕中气泡尺度参数,可提高气泡幕的隔声效果。
2)依据单位面积排气量相等原则开展变孔间距定孔面积设计。在进气初始位开孔压力接近条件下,与均匀开孔排气方案相比,进气口压力约低0.96%,最近排气孔压力高出约0.48%。
3)在相同排气条件下,变距定积排气模型排气效果明显优于均匀排气模型。
| [1] |
张国胜, 顾晓晓, 邢彬彬. 海洋环境噪声的分类及其对海洋动物的影响[J]. 大连海洋大学学报, 2012, 27(1): 89-94. ZHANG G S, GU X X, XING B B. The classification and the impact of marine environment noise on marine animals[J]. Journal of Dalian Ocean University, 2012, 27(1): 89-94. DOI:10.3969/j.issn.1000-9957.2012.01.018 |
| [2] |
MINNAERT M. On musical air-bubbles and sounds of running water[J]. Philosophical Magazine., 1933, 26: 235. |
| [3] |
王红艳, 张法星, 刘昶. 燕尾坎挑流消能噪声的影响因素分析[J]. 水电能源科学, 2019, 37, 228(8): 12-15. WANG H Y, ZHANG F X, LIU C. Analysis of influencing factors of ski-jump energy dissipation noise with dovetail camp[J]. Water Resources and Power, 2019, 37, 228(8): 12-15. |
| [4] |
陆遐龄, 梁向前, 胡光川, 等. 水中爆破的理论研究与实践[J]. 爆破, 2006(2): 23-28. LU X L, LIANG X Q, HU G C, et al. Theoretical research and engineering practice about underwater blasting[J]. Blasting, 2006(2): 23-28. |
| [5] |
罗佳, 白艳勤, 林晨宇, 等. 不同流速下气泡幕和闪光对光倒刺鲃趋避行为的影响[J]. 水生生物学报, 2015, 39(5): 1065-1068. LUO J, BAI Y Q, LIN C Y, et al. The influence of bubble curtain and strobe light to approach-avoidance behavior of Spinibarbus hollandi Oshima in different flow velocity[J]. Acta Hydrobiologica Sinica, 2015, 39(5): 1065-1068. DOI:10.7541/2015.140 |
| [6] |
张文光, 王虹斌. 水中气泡幕声衰减研究[C]//第四届船舶水噪声学术交流会, 1991, 12: 24−27.
|
| [7] |
钱祖文. 水中气泡之间的声相互作用[J]. 物理学报, 1981, 30: 442-447. QIAN Z W. Sound interaction among bubbles in water[J]. Acta Physica Sinica, 1981, 30: 442-447. DOI:10.7498/aps.30.442 |
| [8] |
ELLER A I. Damping constants of pulsating bubbles[J]. The Journal of the Acoustical Society of America, 1970, 47: 1469-1470. DOI:10.1121/1.1912063 |
| [9] |
QIAN Z. Sound propagation in a medium containing bubbles and the splitting of the resonance peak[J]. Journal of Sound & Vibration, 1993, 168: 327. |
| [10] |
WATERMAN P C. New formulation of acoustic scattering[J]. The Journal of the Acoustical Society of America, 1969, 45: 1417-1429. DOI:10.1121/1.1911619 |
| [11] |
DAVIDS N, THURSTON E G. The acoustical impedance of a bubbly mixture and its size distribution function[J]. The Journal of the Acoustical Society of America, 1950, 22: 20-33. DOI:10.1121/1.1906568 |
| [12] |
FOX F E, CURLEY S R, LARSON G S. Phase velocity and absorption measurements in water containing air bubbles[J]. The Journal of the Acoustical Society of America, 1955, 27: 534-539. DOI:10.1121/1.1907955 |
| [13] |
LAIRD D T, KENDIG P M. Attenuation of sound in water containing air bubbles[J]. The Journal of the Acoustical Society of America, 1952, 24: 29-32. DOI:10.1121/1.1906842 |
 2023, Vol. 45
2023, Vol. 45

