0 引　言

横移运动常见于船舶自主停靠港口的场景，此时船舶应满足低速横移时所有推进器可抵抗环境力的操纵能力。由于客滚船或邮轮需要短时间内访问多个港口，在港口接载乘客或者车辆。同时，这类船的上建筑面积较大，受环境力影响较大，如果船舶不能抵抗环境力，容易出现碰撞码头事故。因此，在设计初期评估船舶横移能力十分重要，既能为船东判断船舶的操作方便程度，又能为船厂预订设备提供数据支持。

Yoshimura^[1]研究认为横移运动作用在船舶上的力由横流阻力产生，它与横向速度的平方成比例。Quadvlieg等^[2]基于实验数据提出计算横移运动的简易算法。Lee等^[3]使用常规纵向运动的模型模拟了双尾鳍双舵的横移运动。Yoo等^[4]对客船在无纵向速度下的横移运动的横荡和横摇水动力进行了实验研究。杜海林^[5]和刘春生等^[6]研究双桨双舵船靠码头的操纵运动。陈锦标等^[7]研究了配备双桨双舵和首侧推器船舶的靠泊方案，并给出了某实验船在不同风浪情况下的具体靠泊方案。陈秀嘉^[8]基于MMG建立了3自由度的港内双桨双舵集装箱船的数学模型，较好描述了船舶在实际航行中的操纵性能。Gornicz 等^[9]利用CFD方法进行了船舶横移能力评估。邹璐等^[10]基于CFD研究了邮轮横移运动的水动力机理。国内的研究主要集中在船舶在离靠港口的操纵运动方式，较少研究侧推器等辅助装置对纯横移运动影响，且计算模型较多，参数较难在初步设计时全部获得。

本文在Quadvlieg的简易算法基础上，考虑风载荷影响，应用低速域运动方程，引入横流阻力系数，利用螺旋桨、侧推器、舵和船体的主要参数可快速得到船舶横移能抵抗的最大风速，为客船国产化提供技术依据。

1 计算原理

纯横移运动是衡量双桨双舵船在低速域操纵性的重要指标，当船舶在低速时，在风、浪、流等环境力作用下，螺旋桨推力–舵力无法单独控制船舶平衡，船舶会产生横移和旋转，需要借助侧推器、拖轮、锚等协助才能控制船舶。同时，船舶需要操纵主机频繁换向，利用螺旋桨的尾流增加舵效的方式控制船舶。传统双桨双舵船抵抗环境力的方式如图1所示，螺旋桨采取一正一反的方式，正推螺旋桨后的舵产生升力和阻力，并在侧推器的配合下满足力的平衡。

由于船舶临近港口时受波浪影响较小，因此不考虑船舶的横摇、纵摇和垂荡运动，采用三自由度船舶操纵方程描述低速域操纵性方程^[11]：

$ \left\{ {\begin{aligned} & {\left( {m + {m_x}} \right)\dot u - \left( {m + {m_y}} \right)vr = X}{\text{,}}\\ & {\left( {m + {m_y}} \right)\dot v - \left( {m + {m_x}} \right)ur = Y}{\text{,}}\\ & {\left( {{I_{zz}} + {J_{zz}}} \right)\dot r = N}{\text{。}} \end{aligned}} \right. $

(1)

其中：

$\left\{ {\begin{aligned} & {X = {X_H} + {X_P} + {X_R} + {X_A} + {X_T} ，}\\ & {Y = {Y_H} + {Y_P} + {Y_R} + {Y_A} + {Y_T}，}\\ & {N = {N_H} + {N_P} + {N_R} + {N_A} + {N_T} }{\text{。}} \end{aligned}} \right. $

(2)

式中：m为船舶的质量；m_x和m_y为各方向的附加质量；I_zz为惯性矩；J_zz为附加惯性矩。下标H为裸船体、P为桨、R为舵、A为风、T为侧推器。

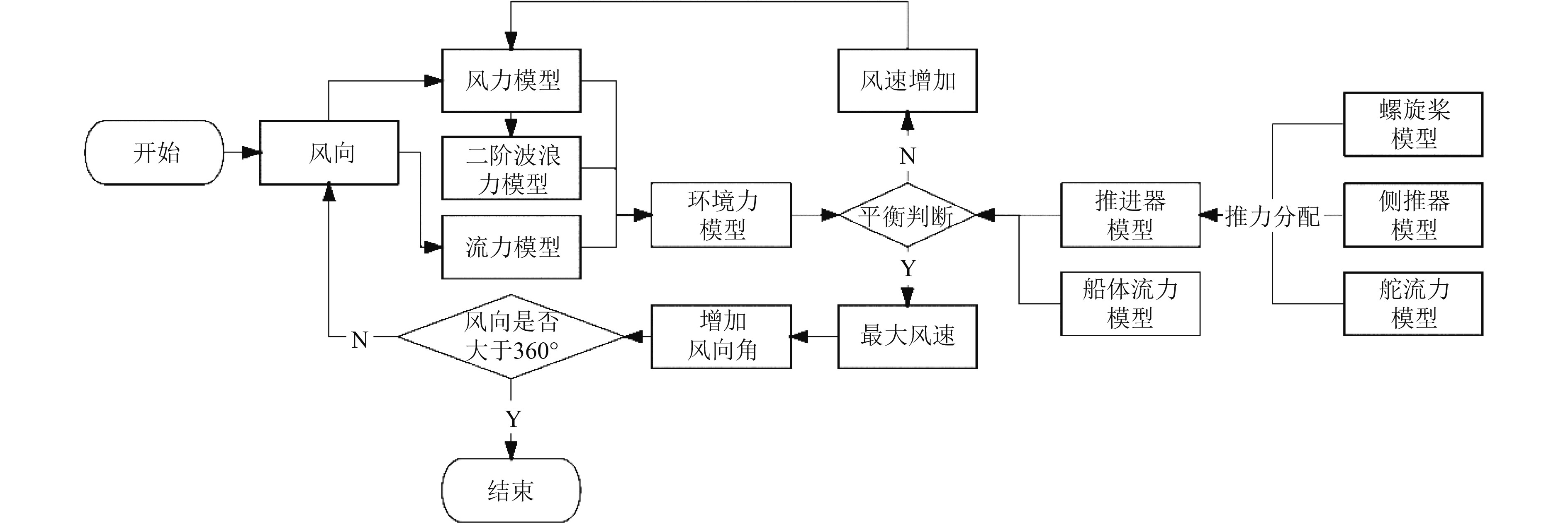
2 计算步骤

假设船舶无前进航速，忽略船、桨、舵和侧推器之间的相互作用，忽略水深、岸壁效应和地域限制，只考虑船舶准静态的横移运动计算，通过计算船舶能承受的各方向最大风速来评判横移运动能力的优劣。由于它可以允许船舶横向移动，因此，当船舶有横向速度时，不仅需要计算推进器各推力和环境力大小，还需计算船舶横向移动产生的流体力和力矩。计算步骤^[12]如图2所示，其中环境力模型只考虑了风力模型。

2.1 船体上流体力和力矩

计算低速域船体上的流体动力和力矩，采用乌野提出的无量纲化模型^[11]：

$ \left\{ \begin{aligned} & {c}{X}_{{H}} = {\frac{1}{2}\rho Ld{V}^{2}(X'} _{{u}{u}}{u}{{'}} \left|{u}{{'}}\right| + {X}_{{u}{v}{v}}{{'}} {u}{{'}} {{v}{{'}}}^{2} + {X}_{{u}{u}{u}{v}{v}}{{'}}{{u}{{'}}}^{2}{{v}{{'}}}^{2} + {X}_{{v}{v}}{{'}}{{v}{{'}}}^{2} ),\\ & {Y}_{{H}}=\frac{1}{2}\rho Ld{V}^{2}\left({Y}_{{u}{u}{v}}{{'}}{{u}{{'}}}^{2}{v}{{'}}+{Y}_{{u}{u}{v}{v}{v}}{{'}}{{u}{{'}}}^{2}{{v}{{'}}}^{3}+{Y}_{{v}{v}{v}}{{'}}{{v}{{'}}}^{3}\right),\\ & {N}_{{H}} = \frac{1}{2}\rho {L}^{2}d{V}^{2} ({N}_{{u}{v}}{{'}}{{u}{{'}}v}{{'}} + {N}_{{u}{u}{v}}{{'}} {{u}{{'}}}^{2}{v}{{'}} + {N}_{{u}{u}{v}{v}{v}}{{'}} {{u}{{'}}}^{2} {{v}{{'}}}^{3} + {N}_{{v}{v}{v}}{{'}} {{v}{{'}}}^{3} )。\end{aligned}\right. $

(3)

其中：V为合速度；u'、v'、X'_uu、X'_uvv等为无因次水动力导数，水动力导数参考文献[11]分析得到的公式。

2.2 推进器的推力模型

螺旋桨推力主要用于计算最大系柱推力和转速，作为推进器模型计算的约束条件。螺旋桨的推力和功率可表示为：

$ {X}_{{P}}=\frac{{\text{π}} }{8}\rho {D}_{{P}}^{2}({u}_{{P}}^{2}+{\left(0.7{\text{π}} n{D}_{{P}}\right)}^{2}){C}_{{T}}\left({\beta }_{{P}{R}}\right) {\text{,}}$

(4)

$ {P}_{{P}}=\frac{{{\text{π}} }^{2}}{4}\rho {D}_{{P}}^{3}({u}_{{P}}^{2}+{\left(0.7{\text{π}} n{D}_{{P}}\right)}^{2})n{C}_{{Q}}\left({\beta }_{{P}{R}}\right){\text{。}} $

(5)

其中：D_P为螺旋桨直径，n为螺旋桨转速，u_P为螺旋桨进速，不考虑前进速度，即u_P=0。对于进速角β_PR，当桨为正推和逆推时分别为0和π；C_T和C_Q表示桨系柱推力和扭矩系数。通常利用推力公式可计算正向螺旋桨推力，利用功率公式和已知的最大逆推功率可推出逆转时最大转速，从而得到逆转时最大推力。

侧推力主要产生横向力，推力与实时功率呈正相关关系，力和功率的转换系数通常为0.1～0.15 kN/kW。本文取该系数为0.13 kN/kW。

2.3 舵的流体动力模型

当螺旋桨正转时，舵处于螺旋桨尾流和船体尾流中。由于船体没有前进速度，则不需考虑船体尾流。当螺旋桨处于逆转状态时，认为桨的尾流不会作用在舵上，舵的来流非常小，因此假设螺旋桨逆推时产生的舵力可忽略不计。舵力计算模型^[13]为：

$\left\{ {\begin{array}{*{20}{c}} {{X_{{R}}} = (1 - {t_{{R}}}){F_{{N}}}{\rm{sin}}\delta }，\\ {{Y_{{R}}} = (1 + {a_{{H}}}){F_{{N}}}{\rm{cos}}\delta }。\end{array}} \right. $

(6)

其中：操舵诱导船横向力的舵力修正因子a_H和操舵引起的舵阻力减额系数t_R均为0；δ为舵角；F_N为舵上的流体正压力，表示为 ${F}_{{N}}=-\dfrac{1}{2}\rho {A}_{{R}}{f}_{{a}}{U}_{{R}}^{2}sin\alpha$ ，尾流速度U_R应考虑舵面临的桨尾流和船体尾流。

由于船体无前进航速，尾流速度可简化为 ${U}_{{R}}={c}_{{U}{R}}\sqrt{\displaystyle\frac{{8X}_{{P},{{\rm{balancing}}}}}{{\text{π}} \rho {D}_{{P}}^{2}}}$ ，其中X_P,balancing表示正转螺旋桨。c_UR综合考虑了舵的增速系数和舵的有效来流面积系数， $ {c}_{{UR}}=0.7\sqrt{\displaystyle\frac{{D}_{{P}}}{{H}_{{R}}}} $ ，H_R为舵高。

2.4 风力模型及风速和高度转换

船舶在海上航行时，上层建筑会受到风力作用，客船具有受风面积较大的上层建筑，风力对船舶操纵的影响尤为显著。作用在船体上的平均风压力和力矩表示为：

$ \left\{ {\begin{aligned} & {{X_{{w}}} = 0.5{\rho _{{a}}}{A_{{f}}}U_{{w}}^2{c_{{{wx}}}}}{\text{,}}\\ & {{Y_{{w}}} = 0.5{\rho _{\rm{a}}}{A_{{s}}}U_{{w}}^2{c_{{{wy}}}}}{\text{,}}\\ & {{N_{{w}}} = 0.5{\rho _{{a}}}{A_{{s}}}L_{oa}U_{{w}}^2{c_{{{wn}}}}}{\text{。}} \end{aligned}} \right.$

(7)

式中：ρ_a为空气密度；A_f为船舶水线以上正投影面积；A_s为水线以上侧投影面积；L_oa为总长。c_wx、c_wy、c_wz表示各方向的风压力（矩）系数，本文使用Blendermann公式^[14]计算风压力和力矩系数，该公式设置的风压中心为船中且距离水线10 m高处。

由于空气的流动与海表面存在摩擦，接近海面风速会降低^[8]。船舶上层建筑不同高度对应的风速不一致，而测量风速的位置在驾驶甲板或者使用风测仪，通常远高于10 m，因此需要通过风速的垂直分布规律将计算的风速转换到测量高度，使用对数规律描述 $U\left(z\right)=\displaystyle\frac{{U}_{{w}}}{k}{\rm{ln}} \displaystyle\frac{z}{10}$ ，k为系数取0.4。

2.5 推力分配

除去给出的3个方向的等式约束条件，还应有螺旋桨推力、侧推力和舵力小于最大值的不等式约束条件。在固定风向角和舵角情况下，可得到多组满足条件的数值，为判断出推进器使用率最高的情况，采用数学函数^[15]为 $\displaystyle\frac{{F}_{{b}}}{{F}_{{b}{m}{a}{x}}}+\displaystyle\frac{{X}_{{P},{{\rm{balancing}}}}}{{X}_{{p \max},{{\rm{balancing}}}}}+ \displaystyle\frac{{X}_{{p},{{\rm{astern}}}}}{{X}_{{p}{\max},{{\rm{astern}}}}}$ 筛选满足约束条件的数值，即认为作用于船舶上各推进器的实际使用情况占各自最大推进器力的百分比之和表示推进器的使用率情况。

3 算例验证和预报 3.1 3200客位客滚船验证

选取3200客位客滚船计算验证，其主要参数如表1所示。该船型分别在MARIN和DSME水池进行了模型试验对比，验证了模型试验数据的有效性。依据给出的经验公式模拟纯横移计算得到结果与文献模拟以及试验结果对比如图3所示。结果表明，本文模拟处于文献模拟数据和试验数据中间，与文献模拟数据接近，但在二三象限对风速的模拟与试验数据相比偏保守。因此，本文计算方法的有效性得到了验证。

3.2 3100 m车道/1000人次客滚船验证

3 100 m车道/1000人次客滚船的主要参数见表1。根据TU Hamburg-Harburg报告提供的参数计算船舶向右横移1 m/s时的风速极限，得到风速极限对比如图4所示的。可以看出，计算值与TU Hamburg-Harburg计算值吻合较好，在180°～190°的计算值偏差较大，但此区域为风速极值较大 的区域，对整体评估的影响不大。结果显示最危险的工况出现在风向为311°，风速为12.1 m/s，而TU给出的结果为风向315°，风速极限在12.5 m/s，说明计算能力能较好的模拟风速极限情况，在应用上是可靠的。船舶向左横移1 m/s的风速极限图与船舶向右横移的趋势基本对称，风速最大值出现在风向为349°，风速极限值为41.3 m/s，最小的风速极限值出现在风向49.3°，风速极限值为11.7 m/s。结合船舶横移的2个工况，当风向在40°～120°以及240°～320°时，船舶能承受的风速较小，风速在11.7～14.9 m/s之间。

3.3 3580 m车道/1300人次客滚船预报

该船以3100 m车道船为母型船，增加船长提高了车辆装载能力，垂线间长和受风面积相应增大，这导致对纯横移运动性能要求提高。

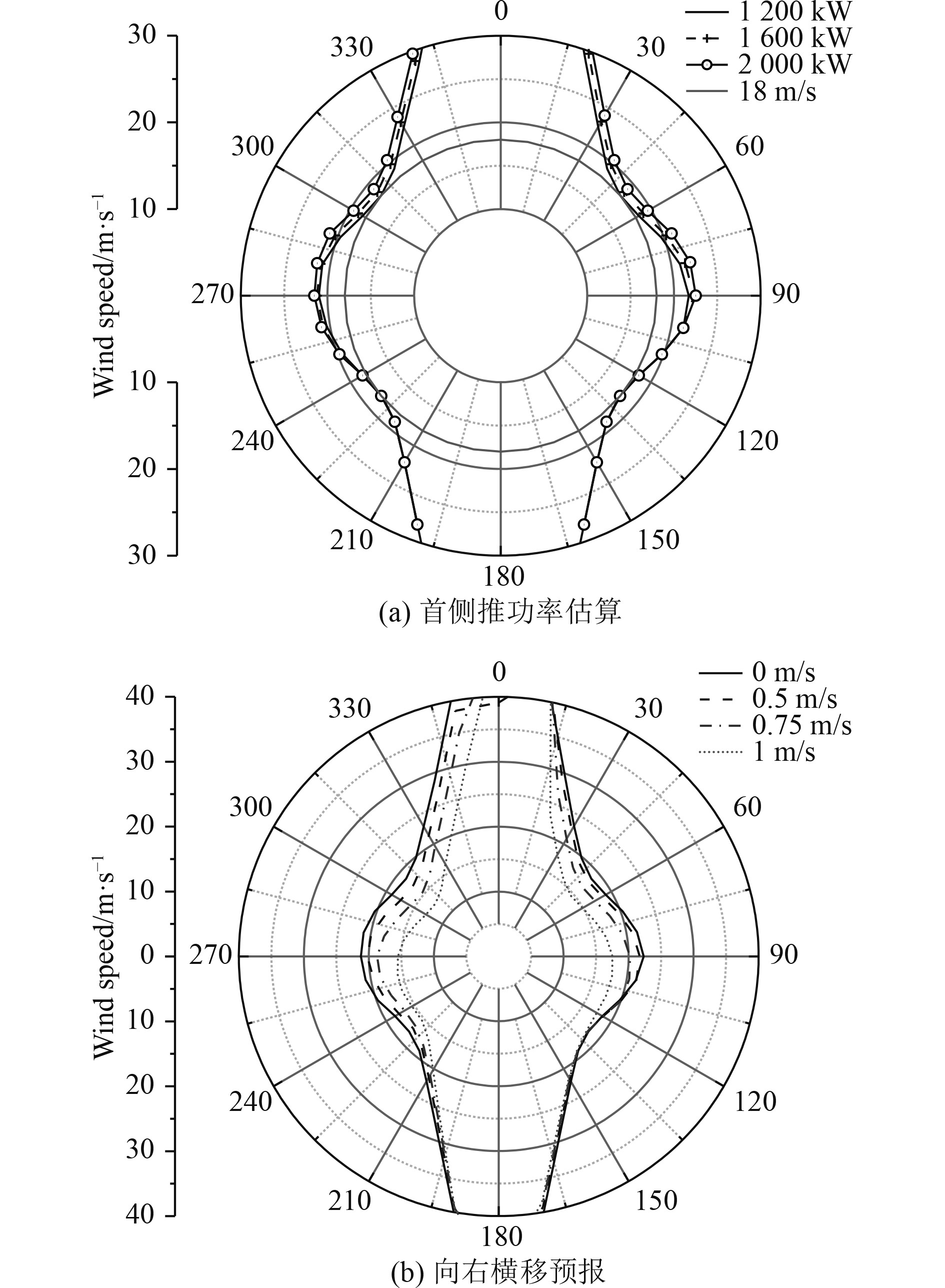
为达到与母型船抵抗风速的同样要求，需要增加1台首侧推。新增首侧推的功率可选型有800 kW、1 200 KW和1 600 kW，图5给出了不同功率的首侧推对船舶纯横移的影响，当新增首侧推功率为1 600 kW时，可满足船舶抵抗18 m/s风速的要求。调整侧推功率的主要改善–100°～100°风向对船舶的影响，对船舶中后部几乎没有帮助，船舶中后部的稳定由螺旋桨和舵共同完成。相对于母型船，本船增加了船长，重心相对前移，主机和舵的尺寸和功率均保持不变，因此船舶中后部能抵抗的风速略有下降。

对该船进行船舶向右横移风速极限预报，船舶横移在135°～210°的风向对风速抵抗的影响不大。当横移0.5 m/s时，船舶可抵抗的风速下降大概在1 m/s，最小抵抗风能力在310°风向约为17.1 m/s；当横移速度为0.75 m/s时，船舶可抵抗的风速下降约2 m/s，在310°风向为15.3 m/s；当横移速度达到1 m/s时，船舶可抵抗的风速下降较大，在310°风向处速度下降至12.7 m/s。

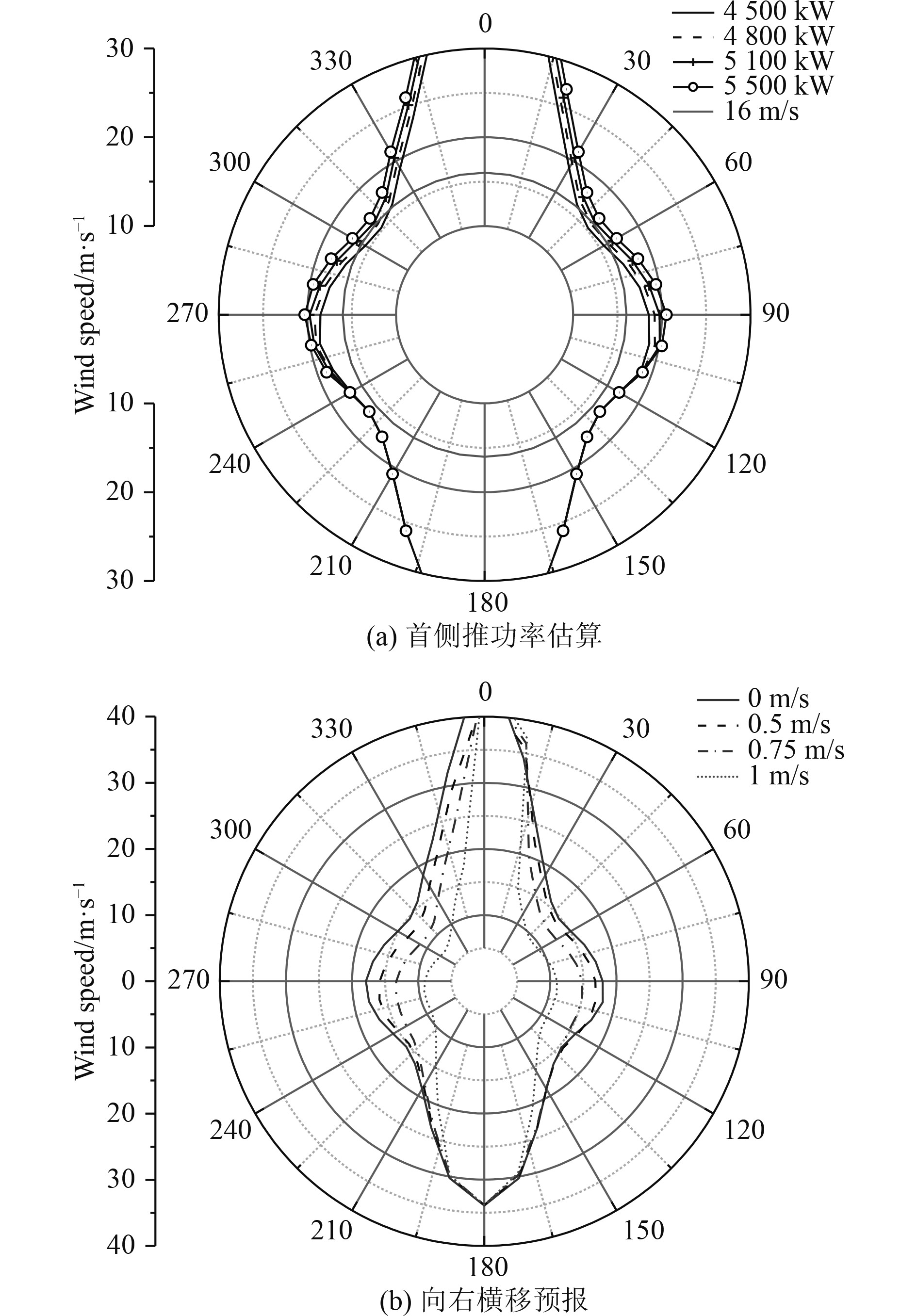
3.4 5100 m车道豪华客滚船预报

对5100 m车道豪华客滚船进行首侧推功率的预报。首先确认船舶应抵抗16 m/s的风速，判断侧推尺寸应小于2.5 m，侧推功率可选型有1 400 kW、1 700 kW和2 100 kW，因此可排列组合出的功率分别为4 500 kW、4 800 kW、5100 kW和5 500 kW，不同功率的首侧推对船舶纯横移的影响如图6所示。当首侧推功率为5100 kW时，可满足风速高于16 m/s。当风向为50°～310°时，船舶抵抗风速的能力最差为16.2 m/s。

对船舶向右横移进行预报，随着横移速度增加，抵抗风速的能力逐渐降低。当横移0.5 m/s时，船舶可抵抗的风速下降大概在1 m/s，最小抵抗风能力在310°风向为14.3 m/s；当横移速度为0.75 m/s时，船舶可抵抗的风速下降约2 m/s，在310°风向为12.1 m/s；当横移速度达到1 m/s时，船舶可抵抗的风速下降较大，在310°风向处速度下降至8.25 m/s。若要满足船舶在横移1 m/s时可抵抗16 m/s的风速，首侧推功率需增加3 700 kW。

4 结　语

本文介绍纯横移运动性能的常用场景，并假设船舶只有横向速度，基于MMG分离建模思想，通过理论推导计算作用于船体的流体力及侧推器产生的推力，并建立舵的流体动力模型。考虑风在不同高度时的干扰，通过风速的垂直分布规律将计算的风速转换到测量高度，建立客滚船的纯横移运动数学模型，据此对各推进器进行推力配比，提供了一种通过纯横移运动快速预报侧推器功率的计算方法。以3艘客滚船为算例，利用构建的数学模型进行验证和预报。对比结果显示，本文提出的快速预报侧推器功率的计算方法有效和可靠。对5100 m车道豪华客滚船和3580 m车道客滚船的侧推器功率进行了快速预报，为合同设计提供技术指标。