2. 哈尔滨工程大学,黑龙江 哈尔滨 150001;
3. 中国人民解放军92595部队,辽宁 葫芦岛 125101;
4. 华中科技大学,湖北 武汉 430074
2. Harbin Engineering University, Harbin 150001, China;
3. No. 92595 Unit of the PLA, Huludao 125101, China;
4. Huazhong University of Science and Technology, Wuhan 430074, China
随着世界海上贸易的加强,港口和黄金水道变得越来越繁忙,交通管制问题也变得更加尖锐和紧迫。为了降低运营成本和优化船舶在特殊条件下的运营,确定相遇或追越船舶受到的水动力问题已经成为一项重点研究。因为只有基于充分、高质量的预测及优化才能减少对港口、航道的船舶数量限制,并同时考虑水运交通安全。
针对船间水动力研究的文献主要分为3类。第一类是试验研究,即收集船间水动力的相关试验数据并与数值实验的结果进行对比分析,主要包括Vantorre[1]、Lataire[2]、Arslan[3]、Sano[4]等开展的一系列关于间距、航速、船体参数以及航道的船间水动力实船试验研究,总结得出了横向力、纵向力、首摇力矩在相遇、追越、浅水、狭窄等情况下的规律。目前仍是航运规范的支撑基础[5],而且基于试验数据的半经验预测模型研究也是目前航行规划的主要基础。如徐言民[5]、Vantorre[6]、Varyani[7]等提出了关于速度、船体参数和间距等因素的水动力预测公式,并与实船试验结果具有较好的吻合度。第二类是理论研究,即基于流体是无粘性、不可压缩、无旋、傅汝德数小,自由表面为壁面等假设,通过细长体法、面元法、粘性流法对船间水动力进行数值求解,主要包括Varyani[8]、Wang[9]、张乐文[10]等通过渐近展开方法,建立时间积分模型,研究了两船会遇和追越时的水动力相互作用规律。第三类是数值仿真预测,即基于现有强大的计算能力,考虑流体的粘性、湍流、波浪影响,采用离散化模型求解 RANS方程,主要包括Chen[11]、Zou[12]、Pinkster[13]等基于RANS方程的数值求解研究,得出了水深、船速、船-船横向间距等因素对船-船水动力相互作用的影响规律。
尽管以上研究已为船间水动力研究提供了很多支撑性的定性规律,但仍存在以下问题:
1)试验研究由于涉及设计参数和环境因素众多,存在耗时长、经费高等问题,目前缺乏广泛的试验研究基础和系统的船间水动力数据。同时,由于相互作用条件和影响参数存在大量可能组合,经验和半经验公式只能针对某些特殊情况。
2) 理论研究仍存在单一任务的局限性,只能单独针对追越、相遇或系泊船等某一情况,而且大多数计算方法仅适用于尺寸相对相似的船舶,考虑船体几何形状和波浪影响的研究目前较少。
而数值方法可以有效弥补以上不足,不仅可以建立统一的船间水动力数学模型,而且可以快速、高效、经济地进行系列重复试验。因此,本文为模拟考虑自由表面影响的多个物体联合运动条件下粘性流体流动,通过控制体积法求解非定常RANS方程以及六自由度(6DOF)运动方程。同时采用VOF模型、SST k-ω湍流模型以及滑移网格建立了一种预测船间水动力相互作用行为的方法,并利用该方法开展了孤立Wigley船体、孤立KCS船体、相互作用Wigley船体以及相互作用KCS船体的水动力特性研究,讨论了不同速度比对船间水动力的影响规律,为研究船舶海上遭遇的可控性问题提供数值预测方法和理论指导。
1 理论基础 1.1 基本控制方案黏性不可压缩流体的纳维-斯托克斯(N-S)控制方程为:
| $ \begin{split} \frac{{\partial {u_i}^\prime }}{{\partial t}} + \frac{{\partial \left( {{U_i}{U_j}} \right)}}{{\partial {x_j}}} =& - \frac{1}{\rho }\frac{{\partial P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\nu \left( {\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}} \right)} \right] -\\ & \frac{{\partial \left( {\overline {{{u'}_i}{{u'}_j}} } \right)}}{{\partial {x_j}}} + {g_i},\end{split} $ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 。$ | (2) |
式中:
利用Boussinesq模型求解雷诺应力张量:
| $ \overline {{{u'}_i}{{u'}_j}} = - {\nu _\tau }\left( {\frac{{\partial {U_i}}}{{\partial {x_j}}} + \frac{{\partial {U_j}}}{{\partial {x_i}}}} \right) + \frac{2}{3}{\nu _\tau }{\delta _{ij}}k 。$ | (3) |
式中:
| $ \left\{ \begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{v_j}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k},\\ \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \omega {v_j}} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {S_\omega }。\\ \end{gathered} \right. $ | (4) |
式中:为
本文使用VOF模型模拟自由液面的变化,模拟水和空气混合的流体,在每一控制体积内,两相体积分数的和为1,第i相方程为:
| $ \frac{\partial {\alpha }_{i}}{\partial t}+\overrightarrow{v}\cdot \nabla {\alpha }_{i}=0,$ | (5) |
随质点
| $ \frac{{\partial \alpha }}{{\partial t}} + u\frac{{\partial \alpha }}{{\partial x}} + v\frac{{\partial \alpha }}{{\partial y}} + w\frac{{\partial \alpha }}{{\partial z}} = 0,$ | (6) |
每一控制体积内体积分数函数:
| $ \phi = \frac{1}{{\Delta V}}\int {\alpha (x,t)} {\rm{d}}V,$ | (7) |
上式转化为:
| $ \frac{{\partial \phi }}{{\partial t}} + u\frac{{\partial \phi }}{{\partial x}} + v\frac{{\partial \phi }}{{\partial y}} + w\frac{{\partial \phi }}{{\partial z}} = 0。$ | (8) |
为了模拟多个物体联合运动条件下粘性流体的流动,有必要使用多个网格区域域并使用附加算法在区域边界之间进行数据交换。本文采用滑移网格算法进行边界之间物理量的交换,计算单元的物理量
| $ u\left( x \right) = \frac{{\displaystyle\sum\nolimits_1^n {{v_1}\varphi ({r_1})} }}{{\displaystyle\sum\nolimits_1^n {{v_1}({r_1})} }} 。$ | (9) |
式中:
采用控制体积法对粘性流体动力学方程式(1)进行数值求解,如下式:
| $ \begin{split} &\frac{1}{\Delta t}\left[{\left(\rho \varphi \right)}^{t+\Delta t}-{\left(\rho \varphi \right)}^{t}\right]\Delta V+{\displaystyle \sum _{f=1}^{{N}_{f}}{\rho }_{f}{\varphi }_{f}{\overrightarrow{u}}_{f}\cdot {\overrightarrow{A}}_{f}}=\\ &\qquad \qquad\qquad {\displaystyle \sum _{f=1}^{{N}_{f}}{\Gamma }_{\varphi }{\left(\overrightarrow{\nabla }\varphi \right)}_{n}\cdot {\overrightarrow{A}}_{f}+{S}_{\varphi }}V 。\end{split} $ | (10) |
式中:
同时,对于动量传递方程的数值解,必须给出或找到水动力压力场,计算节点P周围的一些控制体积上积分连续性方程,如下式:
| $ \begin{split} & \frac{{\left( {{\rho _P} - \rho _P^0} \right)\Delta x\Delta y\Delta z}}{{\Delta t}} + \left[ {{{\left( {\rho u} \right)}_e} - {{\left( {\rho u} \right)}_w}} \right]\Delta x\Delta z+ \\ & \left[ {{{\left( {\rho v} \right)}_n} - {{\left( {\rho v} \right)}_s}} \right]\Delta z\Delta x + \left[ {{{\left( {\rho w} \right)}_t} - {{\left( {\rho w} \right)}_b}} \right]\Delta x\Delta y = 0 。\end{split} $ | (11) |
为了评估船间水动力相互作用数学建模的准确性和所选方法的适用性,选取Wigley船体和KCS船体进行初步的数值试验并与实验研究[2]的数据进行比较分析。
2.1 Wigley船体运动模拟为验证前述船间水动力相互作用数学模型的正确性,现分别针对孤立Wigley船体和相互作用Wigley船体在无限流域运行进行模拟仿真,并与Nobuaki Sakamoto[14]提供的数据进行对比,23种工况均选取傅汝德数Fr=0.51。其中,相互作用工况下,考虑Wigley船体间横向距离
Wigley船体主参数:Lpp=1.905 m,B=0.238 m,T=0.095 m。
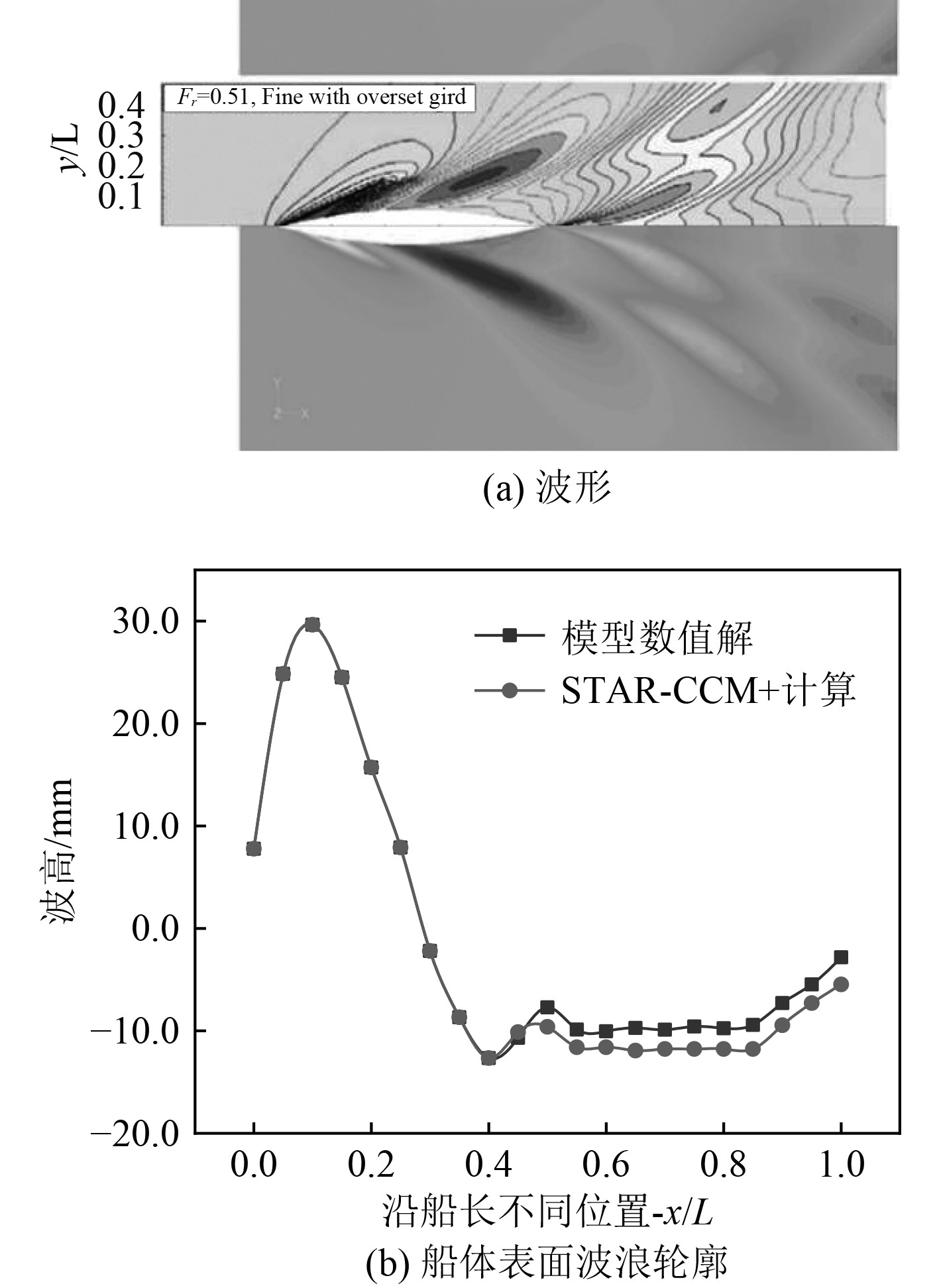
在数值模拟过程中获得的孤立威格利体波形和船体表面的波浪轮廓如图1所示。进一步将文献[14]中试验、仿真计算结果与Wigley模型数值解进行对比,如表1所示。
|
图 1 孤立Wigley船体在Fr=0.51的波型和船体表面波浪轮廓与文献[14]计算结果对比 Fig. 1 Comparison of the wave pattern and hull surface wave profile of the isolated Wigley and the reference [14] |
|
|
表 1 Fr=0.51的阻力系数Cx对比 Tab.1 Comparison of drag coefficient Cx with Fr=0.51 |
阻力系数与实验数据对比表明,使用最高分辨率的计算网格时误差保持在1.4%以内,从而可判断使用前述数学模型可以解决船舶阻力计算问题。
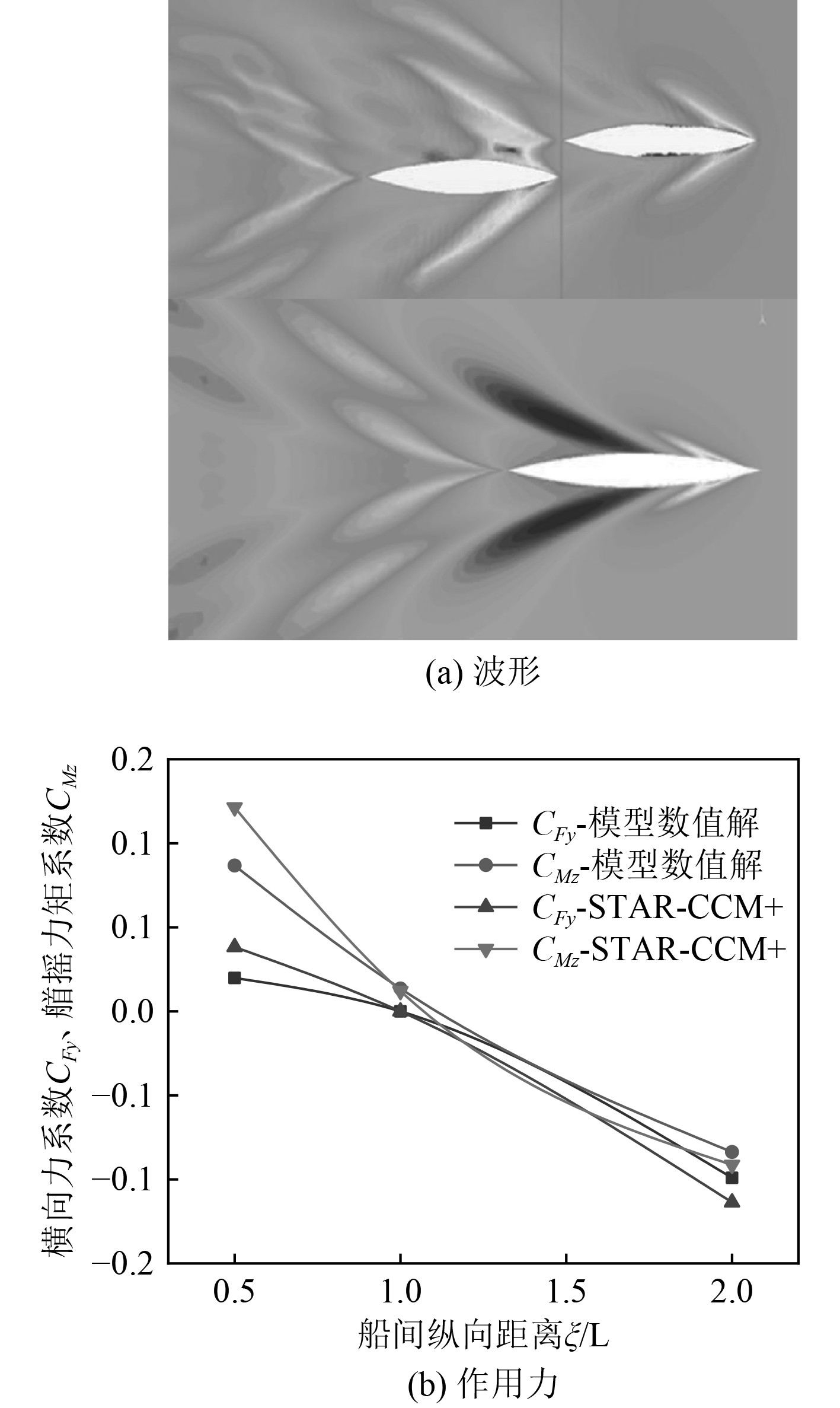
孤立Wigley船体和相互作用Wigley船体模型数值解如图2(a)所示,相互作用Wigley船体模型数值解与STAR-CCM+获得的横向力系数1000CFy、首摇力矩系数1000CMz对比如图2(b)所示。
|
图 2 相互作用Wigley船体在Fr=0.51的波型和与文献[14]作用力计算结果对比 Fig. 2 The wave pattern of the interacting Wigley hull at Fr=0.51 and the comparison with the reference [14] |
从孤立Wigley船体和相互作用Wigley船体模型数值解的波形都可以观察到尾波和船首波以及波浪幅值的增加;目标船船尾波浪系统与追越船头波浪系统相互作用,结果在追越船船头附近形成了一个高度较高的波浪,并且波浪之间的相互干扰在船间区域传播。因此模型数值解所获得的模拟结果可在一定程度下判断前述船间水动力相互作用模型的正确性。
对相互作用过程中的横向力系数1000CFy和首摇力矩系数1000CMz比较分析表明,在船间距离为L/2时结果之间差异最大,但根据著名的实验研究[6,15],目标船处于追越过程,当在船间距离为L时兴波阻力大小和相互作用力矩大小处于最危险时刻。
2.2 KCS船体运动模拟为进一步验证前述水动力数学模型的正确性以及船型对数值模拟的影响,采用缩尺比为1:31.6的KCS船体数学模型进行运动模拟,并将Wigley船体修改成对应参数开展阻力计算结果的对比。同时,将KCS船体计算结果与哥德堡会议[16]的总阻力系数和波形的实验结果进行比较。
缩尺比为1:31.6的KCS船体参数:Lmax=7.357 m,B=1.019 m,T=0.341 77 m。
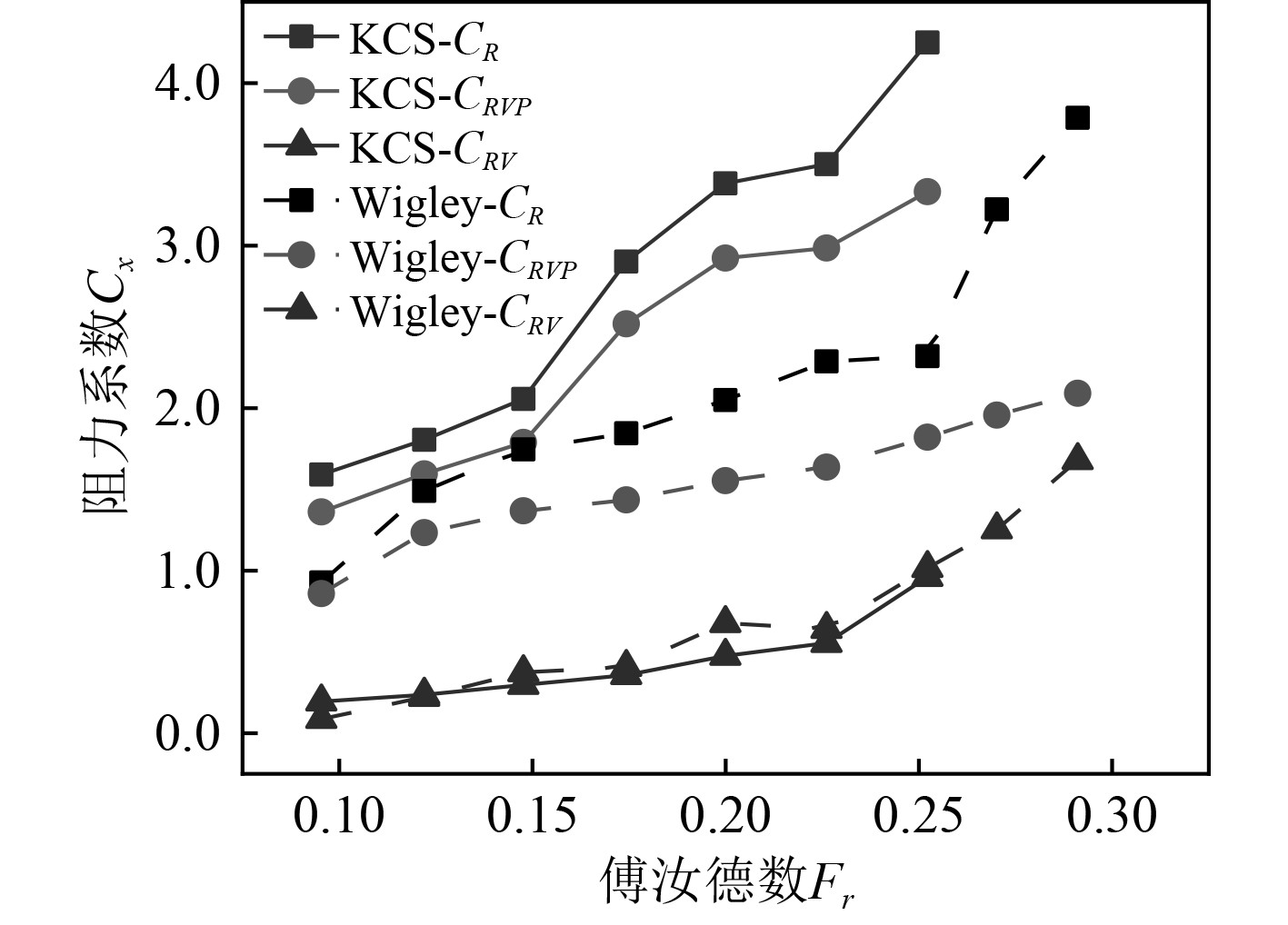
为判断各阻力分量对阻力的影响,尤其是船体形状的影响,将数值模拟的总阻力结果分解为形状阻力(RVP)、兴波阻力(RW)以及粘性阻力(RV)。KCS船体和具有相同基本参数的Wigley船体上的总阻力及其分量结果对比如图3所示。
|
图 3 Wigley船体和KCS船体总阻力及其分量 Fig. 3 Total resistance and components of Wigley hull and KCS hull |
可以发现,当达到Fr=0.25值时,2种情况下粘度成分的影响都会增加,而对于较小的傅汝德数,与船体形状阻力分量优势更明显;而且考虑到波浪形成在Fr<0.2时并不显着,并且在许多情况下兴波阻力的影响可忽略不计。因此,可得出结论,对船舶水动力特性的影响主要与船体形状有关,而且这种形状的影响很可能与船尾的形状有关。
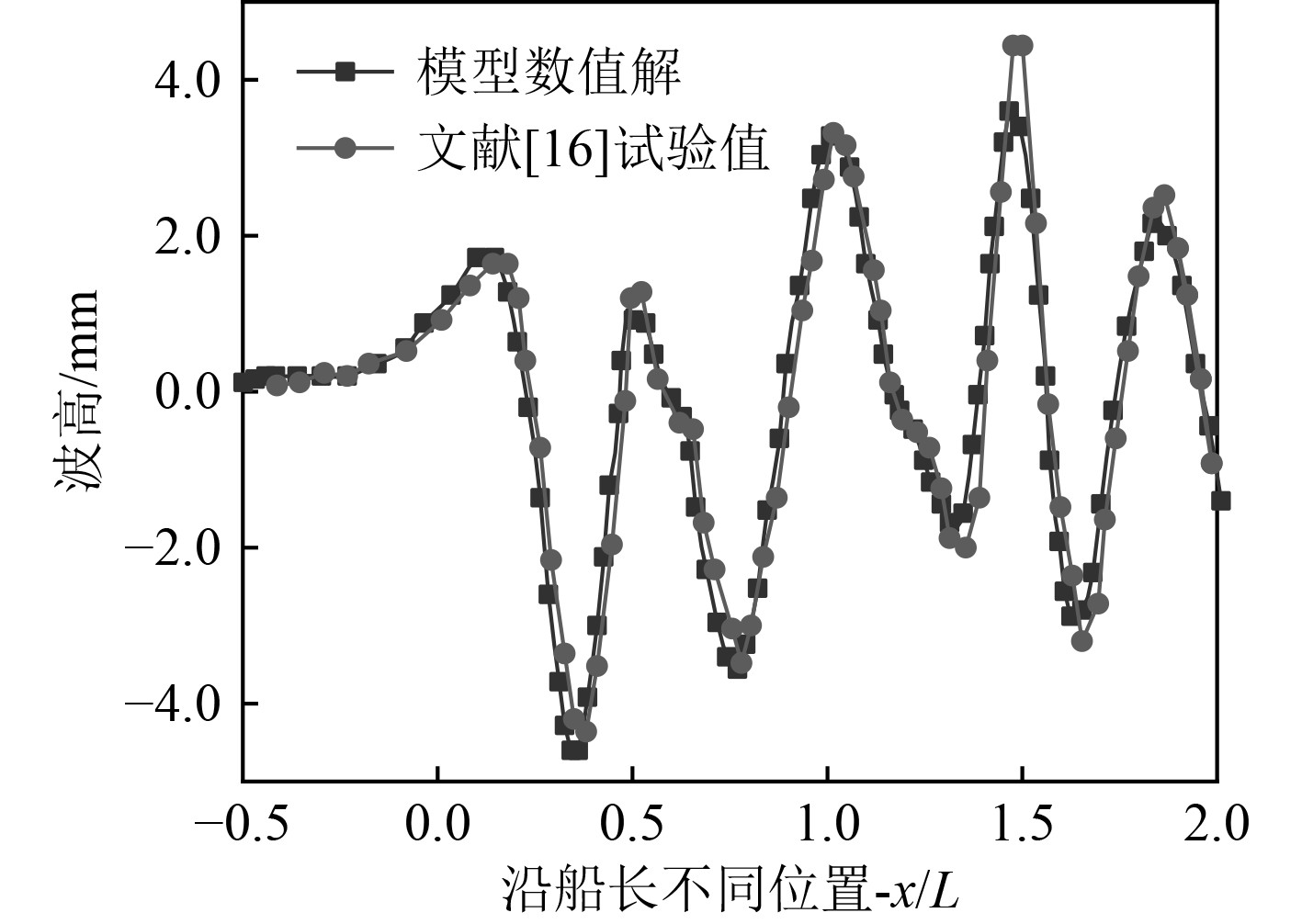
KCS数值解得到的总阻力系数与文献[16]的试验数据对比如表2所示;KCS数值解得到的y/Lpp=0.1509处的波形与文献[16]试验数据对比如图4所示。
|
|
表 2 Fr=0.253的总阻力系数Cx对比 Tab.2 Comparison of total drag coefficient Cx with Fr=0.253 |
|
图 4 试验与数值解在y/Lpp=0.1509处的波形对比 Fig. 4 Waveform comparison between experimental and numerical solutions at y/Lpp=0.1509 |
由表2可知,数值模拟的结果相对于试验得到的值有0.17%的误差。同时数值解与文献[16]中获得试验数据的波廓波形基本一致,因此表明前述水动力数学模型模拟结果可信。
3 运动速度比对船间水动力的影响 3.1 计算模型建立在对多个对象的运动进行建模时(尤其是船舶的水动力相互作用),不同坐标系设置下,船舶位移和旋转方向具有不同的物理意义,因此设置坐标系尤为重要。
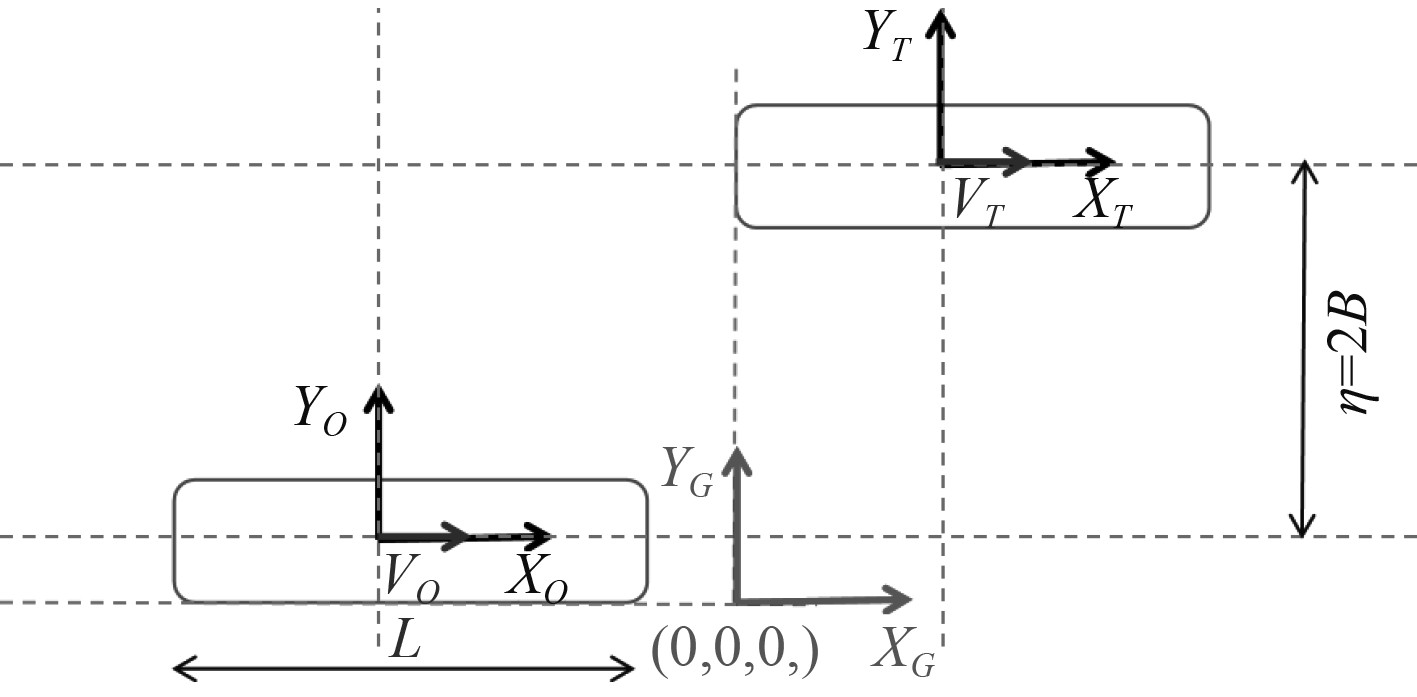
在全局坐标系的基础上为每艘船建立局部坐标系。其中全局和局部坐标系具有相同的轴方向,局部坐标系原点位于重心,全局坐标系原点位移目标船尾部和追越船外舷侧交点,如图5所示。图中O表示追越船、T表示目标船、G表示全局。
|
图 5 追越过程坐标系示意图 Fig. 5 Schematic diagram of the coordinate system of the overtaking process |
KCS船体模型主要参数:Lmax=7.357 m,B=1.019 m,T=0.34177 m。
模型基本设置:动态粘度µ =1.027×10−3 N·s/m2,介质密度ρ=998.4 kg/m3,无限流域。
计算工况设置如表3所示。
|
|
表 3 计算工况 Tab.3 Calculation conditions |
针对工况1分别采用数量为8.65×106和14.5×106网格进行网格无关性验证,所得结果的差异不超过1%。因此认为8.65×106网格分辨率足够用于水动力相互作用的定性和定量分析,其中局部网格细化如图6所示。

|
图 6 KCS船体首部和尾部网格细化 Fig. 6 KCS hull bow and stern mesh refinement |
为综合反映船舶速度、长度、宽度或静止时船的润湿表面的面积对船间水动力的影响,选取无量纲系数作为船间水动力的对比参数。其中,纵向距离系数ξ、纵向力系数CFx、横向力系数CFy、首摇力矩系数CMz定义[17]如下:
| $ \xi = \frac{{2\left( {{\xi _1} - {\xi _2}} \right)}}{{{L_1} + {L_2}}},$ | (12) |
| $ {C_{Fx}} = \frac{{2{F_x}}}{{\rho {V^2}{S_0}}},$ | (13) |
| $ {C_{Fy}} = \frac{{2{F_y}}}{{\rho {{({A^*})}^{1/3}}\left( {V_1^2 - {V_1}{V_2} + V_2^2} \right)}},$ | (14) |
| $ {C_{Mz}} = \frac{{2{M_z}}}{{\rho {{({A^*})}^{1/2}}L\left( {V_1^2 - {V_1}{V_2} + V_2^2} \right)}} 。$ | (15) |
式中:
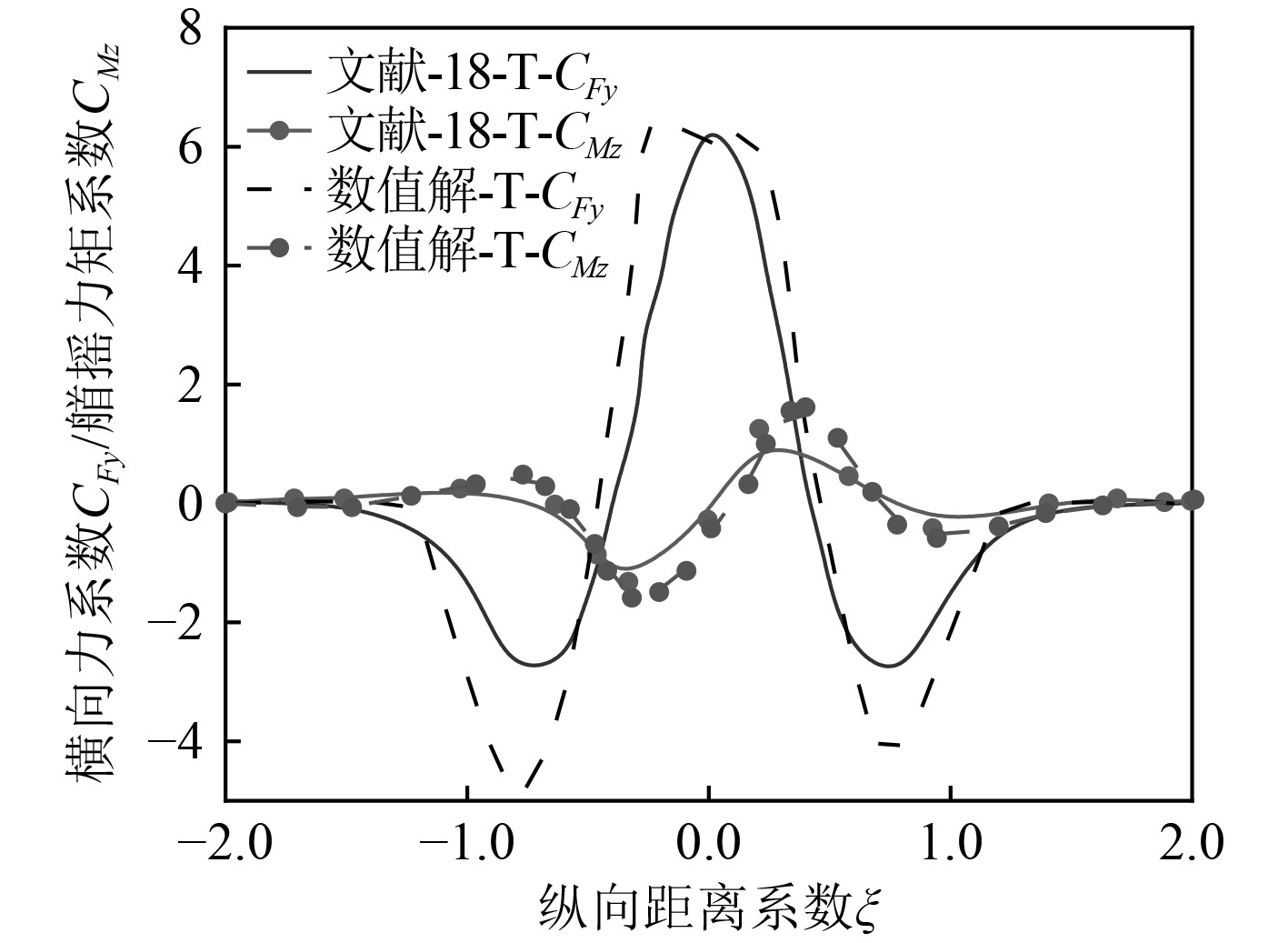
首先,工况1计算得出的目标船上横向力系数CFy、首摇力矩系数CMz数值解与文献[18]中切片势流理论模型结果对比如图7所示。其中,文献[18]中与工况1具有相似的仿真试验条件,而且与Newton[19]试验数据具有相似的规律。
|
图 7 工况1试验与数值解的CFy、CMz对比 Fig. 7 Comparison of CFy and CMz between experimental and numerical solutions under Case-1 condition |
通过分析图7可得出以下结论:
1)本文数值解与理论模型结果具有相似规律,但目标船的横向力系数CFy、首摇力矩系数CMz的峰值存在一定差距;
2)目标船的横向力系数CFy和首摇力矩系数CMz的峰值分布规律具有一致性,分别位于ξ=−0.8、0、+0.8的位置,即追越船(O)船首位于目标船(T)船尾区域、两船并行、追越船(O)船尾位于目标船(T)船首区域;
3)目标船的横向力系数CFy的最大振幅的特征比一致,即追越过程中目标船受到的横向吸力将比排斥力的2倍、2个方向的首摇力矩幅值相等。
工况1计算得出的目标船和追越船上纵向力系数CFx、横向力系数CFy、首摇力矩系数CMz随纵向距离系数ξ的变化如图8所示。可得出以下结论:

|
图 8 工况1数值解的CFx、CFy、CMz Fig. 8 CFx, CFy, CMz of numerical solution under Case-1 condition |
1)追越船(O)的纵向力系数CFx和首摇力矩系数CMz几乎不受静止的目标船(T)影响,但对静止的目标船(T)影响显著;
2)追越船(O)的横向力系数CFy分为3个主要阶段:远离目标船、朝向目标船和远离目标船,该过程与实验研究和实地观察的结果一致。
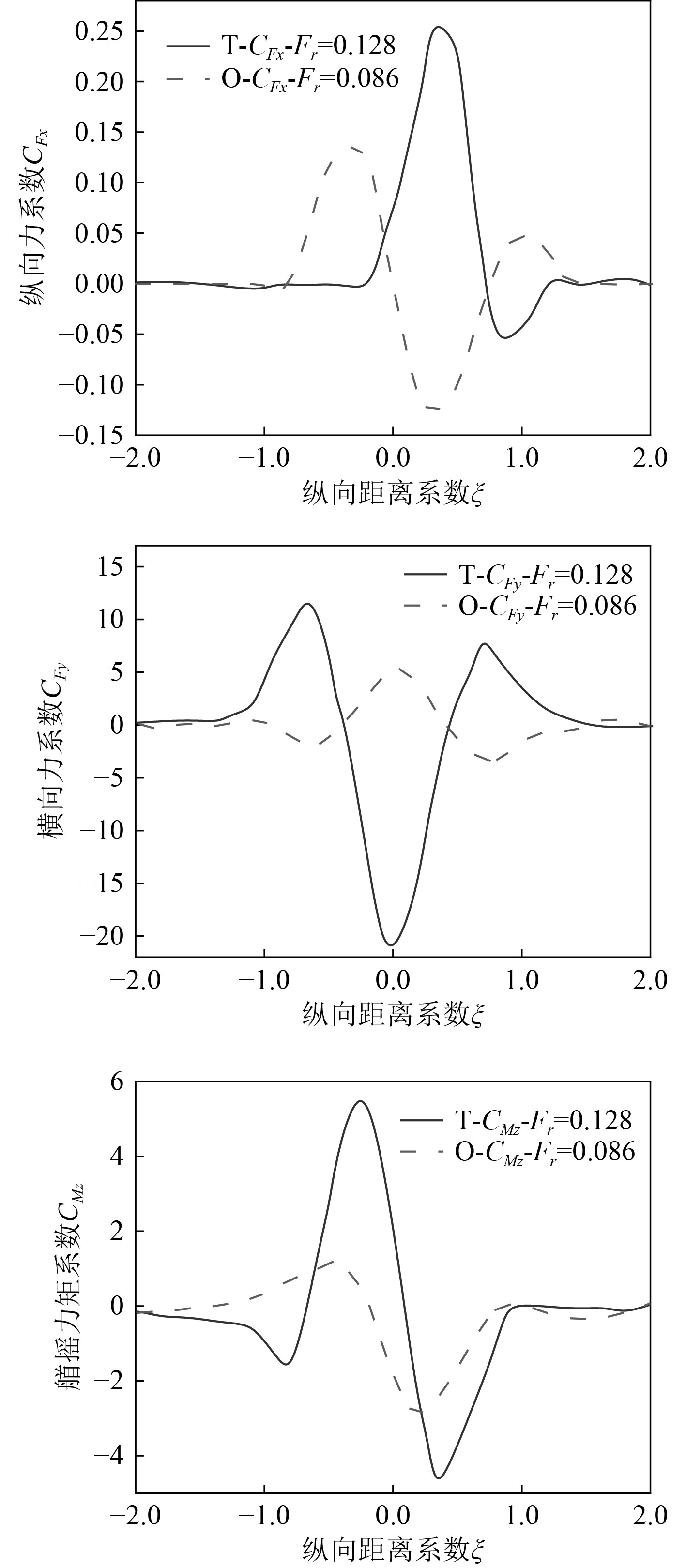
工况2计算得出的目标船(T)和追越船(O)上纵向力系数CFx、横向力系数CFy、首摇力矩系数CMz随纵向距离系数ξ的变化如图9所示。
|
图 9 工况2数值解的CFx、CFy、CMz Fig. 9 CFx, CFy, CMz of numerical solution under Case-2 case |
分析可得出以下结论:
1)追越船(O)的阻力在ξ=−0.8处开始增加、ξ=−0.3处开始减低、ξ=+0.3处逐步增大;
2)追越船(O)在ξ=−0.6处朝向目标船(T)并在ξ=−0.4÷0.4远离目标船(T);
3)追越船(O)船头在ξ=−0.1处远离目标船(T)并ξ=0.2处朝向目标船(T)顺序旋转。
以上数据规律与文献[1]的实验数据变化规律及其幅值具有相似特征:
1)追越船(O)的阻力增加和减少值相等;
2)追越船(O)远离目标船(T)时,横向力最大值时靠近时的2倍;
3)追越船(O)船头远离目标船(T)首摇力矩大约是朝向目标船(T)的1.5倍,而实验值差异为2倍,该差异可能主要来自于船间横向距离不一致。
最后,对比工况1和工况2两种不同目标船船速对水动力系数的影响:
1)2种情况下目标船(T)阻力大小相同,但静止目标船(T)没有反方向的阻力峰值;
2)2种情况下对目标船(T)的横向力和首摇力矩影响相似,但是峰值不同,航速对目标船(T)的首摇力矩影响更显著。
综上所述,对于一艘静止船舶,追越过程中目标船受到的横向力主要受船间纵向距离对其产生的影响;对于一艘航行船舶而言,追越过程中相对航行速度将会对目标船受到的横向力产生很大影响。
4 结 语本文针对船间水动力相互作用问题,建立了一种预测船间水动力相互作用行为的方法,主要得到如下结论:
1)采用本文所构建的船间水动力相互作用预测方法,可以实现对追越船舶的水动力预测,结果与文献符合较好,说明本方法能为研究船舶海上遭遇的可控性问题提供数值预测方法和理论指导。
2)不同速度比下,追越船的阻力增加和减少值相等;追越船(O)远离目标船(T)时,横向力最大值时靠近时的2倍。
3)不同速度比下,目标船的横向力和首摇力矩影响相似,但峰值不同,航速对目标船(T)的首摇力矩影响更显著。
| [1] |
VANTORRE M, LAFORCE E, VERZHBITSKAYA E, Model tests based formulations of ship-ship interaction forces for simulation purposes[C] // IMSF 28th Annual General Meeting, Genova, 2001, 2238–2245.
|
| [2] |
LATAIRE E, VANTORRE M, DELEFOORTRIE G. Captive model testing for ship-to-ship operations[C]// International Conference on Marine Simulation and Ship Manoeuvrability, 2009, 1–10.
|
| [3] |
ARSLAN T, PETTERSEN B, VISSCHER J, et al. A comparative study of PIV experiments and numerical simulations of flow fields around two interacting ships[C]// 2nd International Conference on Ship Maneuvering in Shallow and Confined Water, NTNU, Trondheim, 2011, 31–37.
|
| [4] |
SANO M, YASUKAWA H, KITAGAWA K, et al. Shallow water effect on the hydrodynamic interaction between two ships with rudder in close proximity[C]// 3rd International Conference on Ship Manoeuvring in Shallow and Confined Water, Ghent, Belgium, 2013, 113–121.
|
| [5] |
徐言民, 杨 柯, 关宏旭, 等. 追越情况下船间水动力干扰快速计算模型[J]. 2015, 38(1): 39–43.
|
| [6] |
VANTORRE M. Introduction to maritime technology [R]. Ghent University lecture notes, 2009.
|
| [7] |
VARYANI K, MCGREGOR R, WOLD P. Empirical formulae to predict peak of forces and moments during interactions[C]// Proceedings of the Hydronav – Manoeuvring’99, Gdansk-Ostróda, Poland, 1999, 338–349.
|
| [8] |
VARYANI K S, KRISHNANKUTTY P. Modification of ship hydrodynamic interaction forces and moment by underwater ship geometry[J]. Ocean Engineering. 2006, 33(8): 1090–1104.
|
| [9] |
WANG Q X. An analytical solution for two slender bodies of revolution translating in very close proximity[J]. Journal of Fluid Mechanics. 2007, (582): 223–251.
|
| [10] |
张乐文. 限制水域船体间水动干扰力计算[J]. 中国造船. 1991(1): 28–38.
|
| [11] |
CHEN H C, LINn W M, HWANG W Y. Validation and application of chimera RANS method for ship-ship interaction in shallow water and restricted waterway[C]// Proceedings of 24th Symposium on Naval Hydrodynamics, July, 2002, Fukuoka, Japan.
|
| [12] |
ZOU L, LARSSON L. Numerical predictions of ship-to-ship interaction in shallow water [J]. Ocean Engineering. 2013, 72: 386–402.
|
| [13] |
PINKSTER J A, BHAWSINKA K. A real-time simulation technique for ship-ship and ship-port interactions[C]// 28th Int. Workshop Water Waves Floating Bodies, L'Isle sur la Aorgue, France, 2013
|
| [14] |
NOBUAKI SAKAMOTO, WILSON R V, et al. Reynolds-averaged Navier-Stokes simulations for high-speed Wigley hull in deep and shallow water[J]. Journal of Ship Research, 2007, 51(3): 187-203. DOI:10.5957/jsr.2007.51.3.187 |
| [15] |
MASTUSHKIN Y M. Hydrodynamic interaction of vessels during meetings and overtaking[J]. Shipbuilding, 1987, 3: 124-125. |
| [16] |
LARSSON L, STERN F, VISONNEAU M. A Workshop on numerical ship hydrodynamics proceedings[C]// Gothenburg, 2010, 2, 137–245.
|
| [17] |
FONFACH J M A, SUTULO S, GUEDES SOARES C. Numerical study of ship-to-ship interaction forces on the basis of various flow models[C]// Proceedings of the 2nd International Conference on Ship Manoeuvring in Shallow and Confined Water: Ship to Ship Interaction, 2012.
|
| [18] |
SKEJIA R, FALTINSEN O M. A unified seakeeping and maneuvering analysis of two interacting ships[C]// Center of Ships and Ocean Structures, Norwegian University of Science and Technology, Trondheim, Norway, 209–218.
|
| [19] |
NEWTON R N. Some notes on interaction effects between ships close aboard in deep water[C]// 1st Symposium on Naval Maneuverability, Washington, USA, 1960: 1–24.
|
 2023, Vol. 45
2023, Vol. 45
