2. 扬帆集团股份有限公司,浙江 舟山 316100
2. Yangfan Group Limited by Share Ltd., Zhoushan 316100, China
2021年10月发布的《关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》和《2030年前碳达峰行动方案》要求经济社会发展要提高自身减排指标,加速建立碳达峰、碳中和“1+N”的制度,为此各产业积极调整运输结构,发展绿色交通。水路运输是重要的运输方式,相对于铁路、高速公路等具有架设成本低、运货量大的经济优势,但由于近几年新冠疫情导致的外贸市场萎靡,航运业在近5~10年的发展前景也不容乐观。其中,燃油成本接近总营运成本的45%~60%。降低船舶燃油消耗是降低营运成本的有效手段。
船舶航速优化是降低船舶燃油成本的有效手段之一,船舶航速优化现在常用的算法有遗传算法(GA)、粒子群算法(PSO)和模拟退火算法(SAA)等。但传统的算法存在编写复杂、计算时间较长、容易陷入局部最优解等问题。人工蜂群算法(Artificial Bee Colony, ABC)因其过程简单、计算容易、需调整参数较少以及收敛速度具有竞争力等优点而在近几年被广泛关注和研究[1-6]。
1 船舶航速优化原理根据相关研究,在设计航速的基础上降低2~3 kn,将大大降低船舶的油耗,降低营运成本[7],所以,船舶航速优化是船舶优化管理中的重点。但是,降低船舶航速也会带来一些新的问题。例如,航速降低会延长船舶航行时间,拉低主机燃油利用率,从而提高了每段航程的燃料消耗。
一些业内人士认为,在油价下跌时,船队可选择提高船舶航速,降低航行期间的其他成本,获得更多收益。但实际上,海运市场上需要运输的货物总量是已确定。海运市场持续低迷,航运公司找不到足够的托运人。因此,航运公司仍然可选择低速航行来获取更多利润。但是,在分析减速过程中存在的其他不利因素后,通过一定方法确定船舶的经济航速十分必要。
2 船舶油耗模型主机油耗是航行成本中最重要的部分,通过构建主机油耗模型,计算耗油量,然后与实船数据进行比较。如果模型计算结果和实际数据相近,则可通过主机油耗模型提出船舶航行时油耗量更低的推荐航速。
船舶主机油耗量Q的计算公式[8]为:
| $ Q = {g_e} \cdot Pe \cdot t 。$ | (1) |
式中:ge为主机油耗率,g/kw·h;Pe为主机输出功率,kW;t为航行时间,h。
可知,主机耗油量可以根据主机油耗率、主机输出功率和航行时间计算得出。其中主机功率与转速的关系式为:
| $ {P_e} = \frac{{{K_Q}\rho {D^5}n_p^3}}{{9\;550{\eta _s}{i^3}}}。$ | (2) |
式中:n为主机转速,r/min;i为轴系传动设备减速比。当船舶在特定工况下稳定航行时,螺旋桨推进系数和扭矩系数均为常数,因此主机功率和主机转速的关系可简化为:
| $ {P_e} = c{n^3} 。$ | (3) |
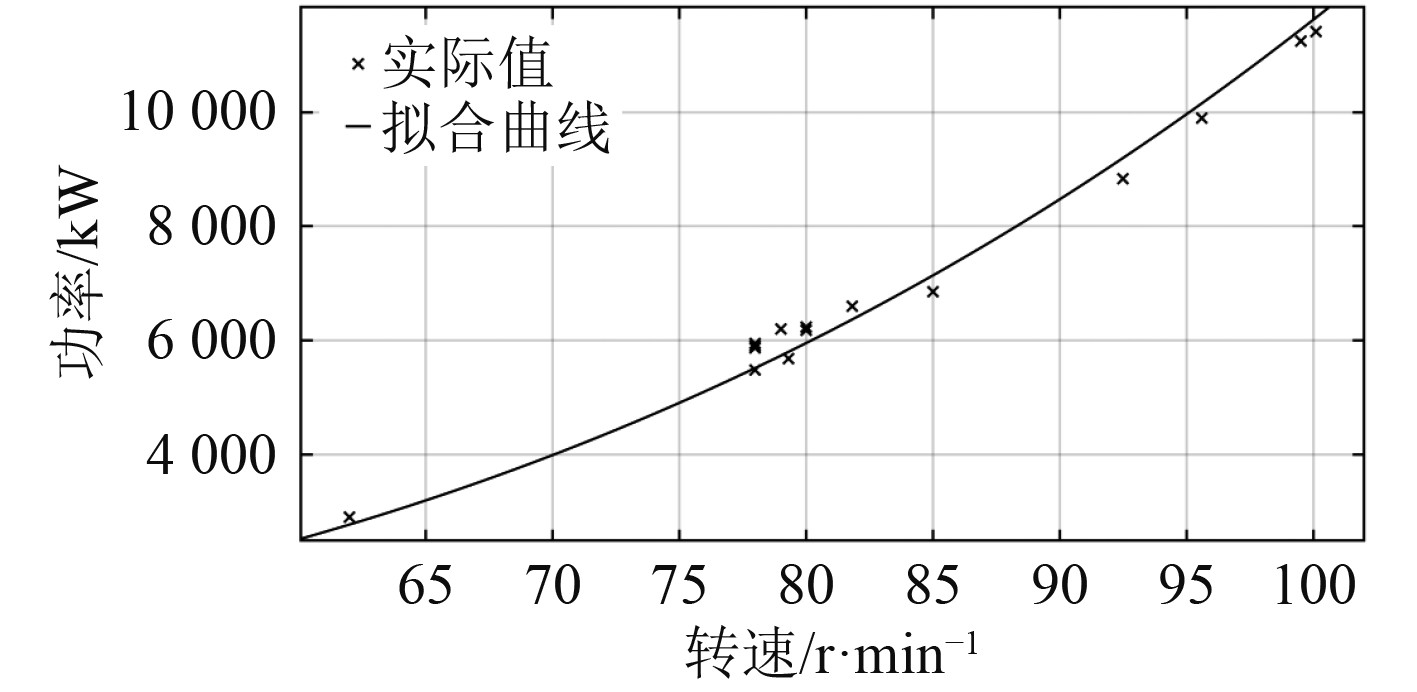
当船舶在特定工况下稳定航行时,系数c为常数。主机输出功率与转速之间的关系同样满足上式,即主机功率与主机转速的三次方成正比。参考船舶主机轴功率监测报告中的数据进行拟合,得到主机功率和主机转速的关系式:
| $ {P_e} = 0.012\;07{n^3} 。$ | (4) |
主机功率与主机转速经过拟合得到曲线如图1所示。
|
图 1 主机输出功率与主机转速关系 Fig. 1 Relationship between output power and rotation speed of main engine |
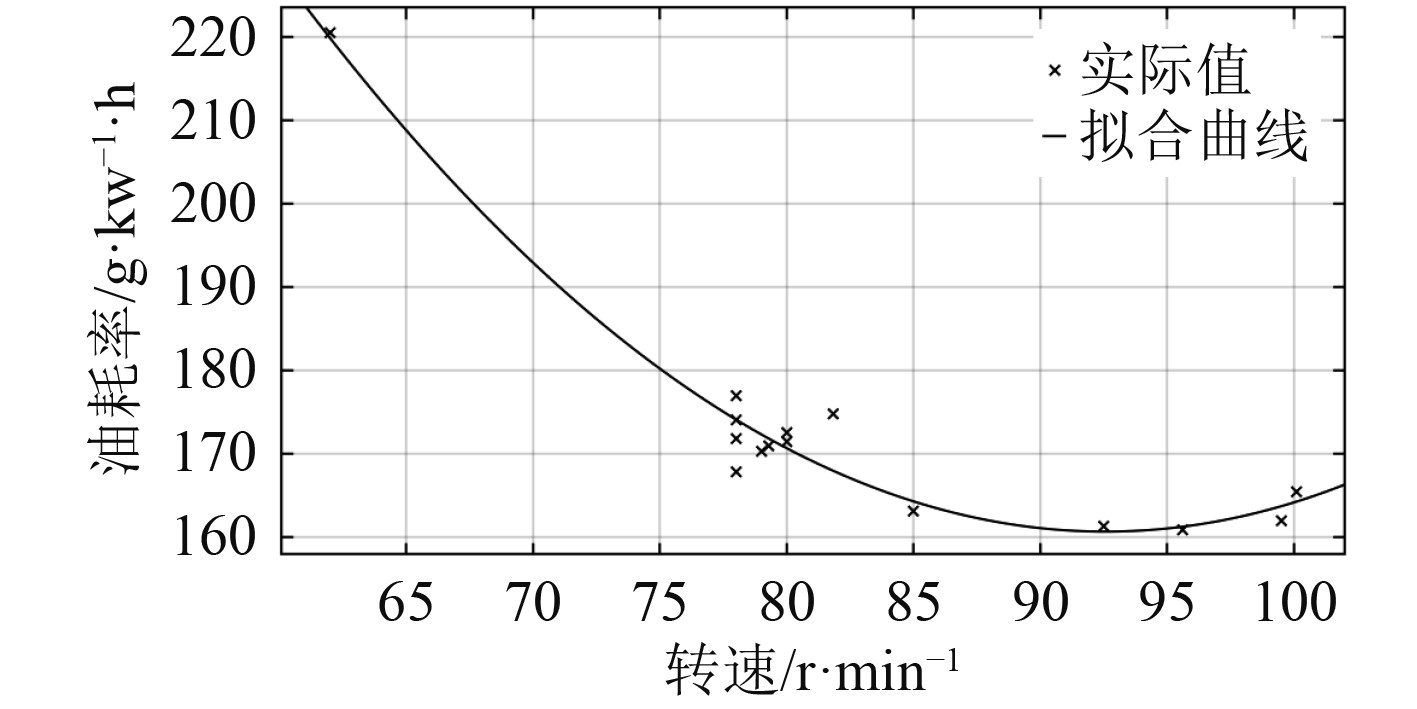
主机正常运转时,燃油消耗率ge、主机功率Pe和主机转速n具有一定的相关关系,但无法建立准确的函数关系式。为获得较为准确的燃油消耗率,可参考船舶历史营运数据并结合式(1),建立数据库并拟合主机转速与燃油消耗率的表达式,现经过计算和拟合得到:
| $ {g_e} = 0.063\;35{n^2} - 11.73n + 703.5。$ | (5) |
主机转速与燃油消耗率经过拟合得到曲线如图2所示。
|
图 2 主机转速与燃油消耗率关系 Fig. 2 Relationship between main engine speed and specific fuel consumption |
由于船舶匀速航行的过程可视为准静态过程[9],船舶所受到的阻力等于螺旋桨的有效推力。为降低主机油耗,从而优化航速,需确定船舶受到的阻力。船舶在航行过程中主要受到静水阻力Rf、风力增阻Ra和波浪增阻力Rw的影响,这3种阻力的表达式为:
| $ {R_f} = Ct\frac{1}{2}\rho V_s^2{S_s}。$ | (6) |
式中:Ct为水阻力系数;Ss为船舶湿面积。
| $ {R_a} = {C_a}\frac{1}{2}{\rho _a}V_a^2{A_s} 。$ | (7) |
式中:Ca为空气阻力系数;Va为相对风速;As为船舶水线以上正投影面积。
| $ {R_w} = 2\int_{ - {\text{π}}}^{\text{π}} {G(\alpha - \chi )\left[ {\int_0^\infty {S\left( f \right)\frac{{\Delta \left( {f,\alpha } \right)}}{{\zeta _A^2}}{\rm{d}}f} } \right]} {\rm{d}}\alpha 。$ | (8) |
式中:G为入射波的方向分布;α为入射波初始方向;χ为波浪入射角;S(f)为入射波频率分布;
当特征波高为1.5 ~ 2 m时,可由Kreitner公式计算,即
| $ {R_w} = \frac{{0.64\zeta _A^2{B^2}{C_b}\rho g}}{L}。$ | (9) |
式中:B为船宽;Cb为方形系数;L为船长。
螺旋桨有效推力为:
| $ {T_p} = (1 - t){K_t}\rho n_p^2{D^4} 。$ | (10) |
式中:t为推力减额;Kt为螺旋桨推力系数。
所以,螺旋桨转速的表达式为:
| $ {n_p} = \sqrt {\frac{R}{{(1 - t){K_t}\rho {D^4}}}} 。$ | (11) |
参照螺旋桨工作特性可知,推力系数Kt是一个随螺旋桨转速而存在小幅度的变化参数,即当船舶在特定工况下稳定航行时,可认为主机转速与船舶航速近似满足线性关系,如下:
| $ {n_e} = a{V_s} + b 。$ | (12) |
根据式(5)~式(12)可知,主机油耗量与船舶航速存在一定的函数关系,当获得船舶航速数据时,可计算得出主机油耗量。
3 人工蜂群算法人工蜂群算法是模仿蜂群采蜜行为提出的一种新型智能算法,每个蜜蜂个体按照各自的分工进行不同的活动,蜂群内部对于有关蜜源信息会进行共享和交流,最终达到高效寻找最优解的目标。人工蜂群算法属于集群智能算法的一种。根据分工不同,可将蜂群分为引领蜂、跟随蜂和侦察蜂[10-12]。蜂群的目的是寻找花蜜最多的蜜源。在ABC算法中,引领蜂的数量和蜜源数量相等。引领蜂可存储发现的蜜源信息,并以一定的概率与跟随蜂进行信息交换;跟随蜂按照引领蜂分享的蜜源信息寻找蜜源;侦察蜂的任务是跳出现有信息,寻找一种新的有价值的蜜源,它们在蜂巢附近随机搜寻,以发现新的有价值蜂源人工蜂群采蜜和具体优化问题的对应关系如表1所示。
|
|
表 1 人工蜂群采蜜和具体优化问题的对应关系 Tab.1 Relationship between artificial bee colony honey harvesting and specific optimization problems |
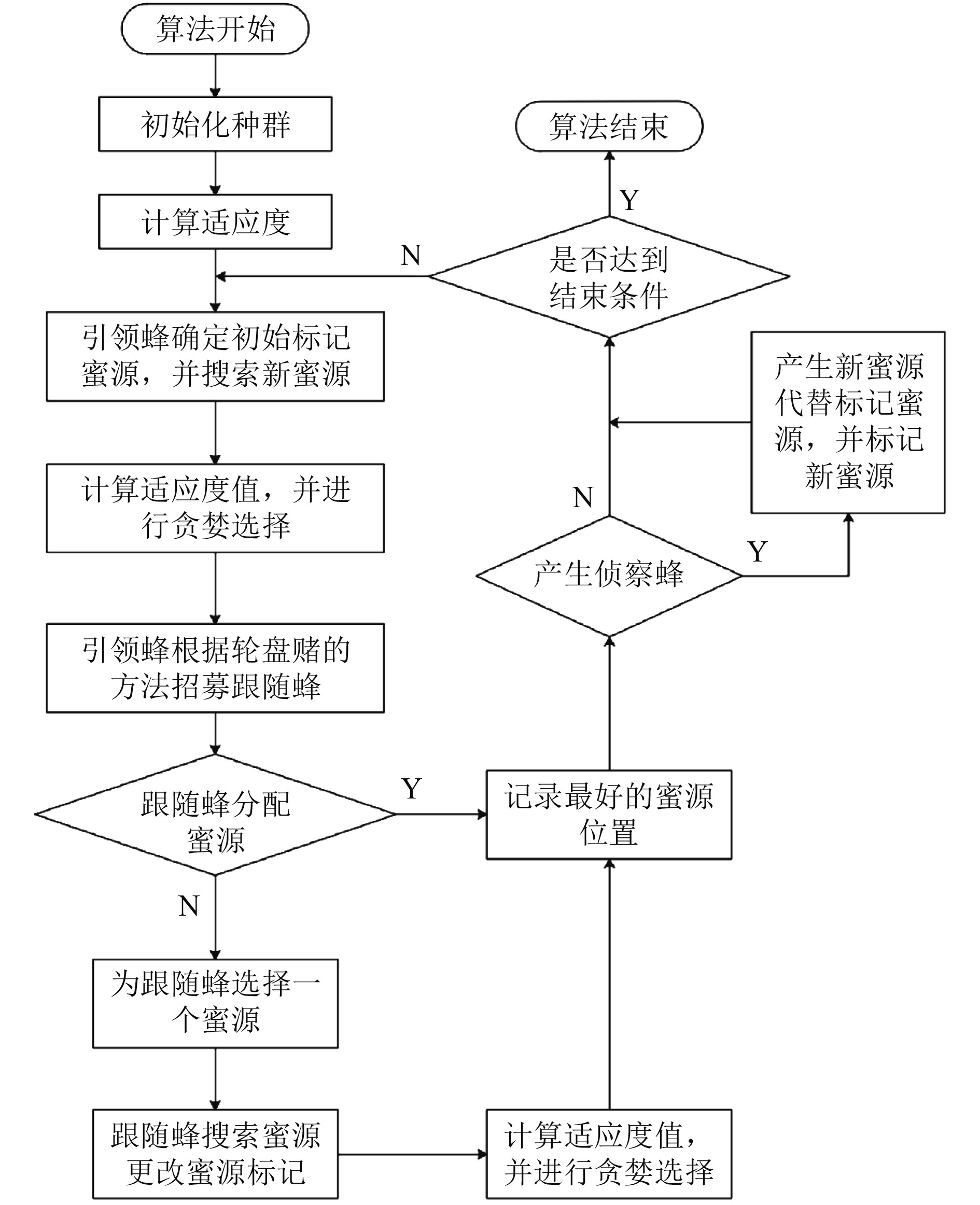
人工蜂群算法流程如图3所示。算法开始阶段需对整个系统初始化,然后引领蜂搜索蜜源最优解,找到蜜源后,跟随蜂确定是否跟随,从而加速问题的收敛。如果蜜源在一定时间内未更新,则引领蜂转化为侦察蜂,提高摆脱局部最优解的能力。
|
图 3 人工蜂群算法流程图 Fig. 3 Flow chart of artificial bee colony algorithm |
在蜜源初始化阶段,需对整个系统的参数进行设置:产生初始蜜源、定义蜜源数量和质量、确定最大迭代次数、确定变量个数并形成变量矩阵、定义尝试阈值等。在人工蜂群算法中,蜜源数量、引领蜂数量和跟随蜂数量相等。
设目标函数的维度为D,即每个蜜源是一个D维向量,在某个蜜源i(i=1,2,…,N,N为引领蜂或跟随蜂的数量)附近进行采蜜的位置表示为xid。对于i个蜜源,根据式(13)确定它的位置:
| $ {x_{id}} = {L_d} + {\rm{rand}}\left( {0,1} \right)\left( {{U_d} - {L_d}} \right) 。$ | (13) |
式中:xid为随机蜜源;Ld、Ud分别表示搜索空间的上、下限值,d=1,2, …,D。
此外,每个蜜源的适应度为:
| $ {f_i} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{1 + f({x_i})}},f({x_i}) \geqslant 0} ,\\ {1 + \left| {f({x_i})} \right|,f({x_i}) < {\text{0}}} 。\end{array}} \right. $ | (14) |
式中,
按照适应度由大到小进行排序,适应度较高的一般视为引领蜂,适应度较低的一半视为跟随蜂。
3.1.2 引领蜂阶段搜索开始前,引领蜂在蜜源i附近根据下式寻找一个新的蜜源:
| $ x_{id}^{\rm new} = {x_{id}} + a \cdot \varphi \left( {{x_{id}} - {x_{jd}}} \right)。$ | (15) |
式中:
比较新、旧蜜源的适应度值,并根据贪婪选择规则,筛选出适应度较高的蜜源,从而对具体问题的解决向着最优解的方向前进。
3.1.3 跟随蜂阶段当引领蜂获得优质蜜源的信息后,返回蜂巢分享获得所有蜜源的信息,跟随蜂以一定的概率选择一只搜索到较高质量蜜源的引领蜂,跟随该引领蜂前往蜜源位置并寻找新的蜜源。那么跟随蜂选择引领蜂的概率为:
| $ {P_i} = \frac{{fi{t_i}}}{{\displaystyle\sum\nolimits_{i = 1}^N {fi{t_i}} }} 。$ | (16) |
式中:
在搜索时,如果一个蜜源经过trial次采集达到阈值L还没有更新为更好的蜜源时,该蜜源就会被摒弃。引领蜂转变为侦察蜂,按照式(17)随机找到一个新的蜜源,侦察蜂找到那个蜜源的位置为:
| $ {x_i} = \left\{ {\begin{aligned} &{{L_d} + {\rm{rand}}\left( {0,1} \right)\left( {{U_d} - {L_d}} \right),trial \geqslant L} ,\\ &{{x_i},trial < L} 。\end{aligned}} \right. $ | (17) |
主机功率与航速的关系为:
| $ {P_e} = \frac{{{\Delta ^{\frac{2}{3}}} \cdot {v^3}}}{C} 。$ | (18) |
式中:
由式(1)和式(18)可知,主机功率和航速是三次方的关系,主机油耗会随着航速的提高而大幅提高。而航速降低会延长航期,增加船舶主机及其他动力装置的负荷[13]。因此航段划分要在保证船舶航行安全的前提下,提高船舶航行能效。此外,在进行航段划分时,要考虑水文、气象等因素,使得船舶在一个航段内航行环境变化较小,保证船舶在较稳定的工况下匀速航行[14]。因此,船舶航段划分的原则总结如下:船舶航向基本不变;水文、气象条件相似。在航段内,假设船舶匀速航行,船舶航速与主机转速一一对应。
在进行航段划分后,假定在同一个航段中,船舶航行时的船舶航速、主机输出功率、主机转速、燃油消耗率等保持不变。
4.2 航段划分实例基于以上航段划分原则,将某散货轮的航行数据,采用人工蜂群算法,以一条从泰国林查班到深圳蛇口的国际航线作为研究对象,对其进行航速优化的相关研究。具体航程如图4所示,按照上文所述分段原则将整个航程分为10个航段,分别是L1、L2……L10,表2详细列出了每条航段的里程信息。此外,该船舶整个航程为1459.1 n mile,船舶航行时间为96.32 h。

|
图 4 航段划分 Fig. 4 Divided voyage section |
|
|
表 2 航迹分段信息 Tab.2 Information of voyage section |
由航迹分段信息表2可知,目标船在10个划分的航段内总的航行时间为96.3 h,总油耗为97.6 t。为验证油耗模型的准确性,将原本航速代入油耗模型中,计算耗油量。
如表3所示,经过计算,油耗模型总油耗为96.8 t,与油耗实际值的误差仅为0.813%,因此可以验证模型的准确性。
|
|
表 3 油耗模型计算结果 Tab.3 Calculation results of fuel consumption model |
对于船舶航速的优化,人工蜂群算法的目标函数是船舶整个航程的总油耗量。通过综合分析,建立了油耗模型,确立了船舶航速和油耗的对应关系,对整个航程进行了分段,接下来确定边界条件,采用人工蜂群算法对每个航段的最低油耗进行计算,并得到油耗最低对应的航速。
| $ Q = \sum\limits_{i = 1}^{10} {{Q_i}}。$ | (19) |
可知,每段航程的油耗量为:
| $ {Q_i} = {g_{ei}} \cdot {P_{ei}} \cdot {t_i}。$ | (20) |
式中:
其中,
| $ {t_i} = \frac{{{L_i}}}{{{V_i}}} 。$ | (21) |
通过营运数据并结合前文对于主机转速和船舶航速的分析,可得出船舶在不同航段内主机转速与船舶航速的函数关系:
| $\left\{ {\begin{array}{*{20}{l}} {{n_{e1}} = 2.026{V_{s1}} + 45.99} ,\\ {{n_{e2}} = 1.971{V_{s2}} + 50.03} ,\\ {{n_{e3}} = 1.762{V_{s3}} + 53.80} ,\\ {{n_{e3}} = 1.885{V_{s4}} + 50.26} ,\\ {{n_{e5}} = 1.837{V_{s5}} + 51.87} ,\\ {{n_{e6}} = 1.823{V_{s6}} + 52.75} ,\\ {{n_{e7}} = 2.033{V_{s7}} + 46.92} ,\\ {{n_{e8}} = 2.044{V_{s8}} + 46.58},\\ {{n_{e9}} = 2.030{V_{s9}} + 46.99} ,\\ {{n_{e10}} = 2.016{V_{s10}} + 36.80} 。\end{array}} \right. $ | (22) |
当船舶航行时,该散货轮的主机正常工作时转速在62~96 r/min的区间内。因此,根据主机转速与航速的关系,可确定船舶航速在10个航段上的上下限约束条件:
| $ \left[ {LB,UB} \right] = \left[ {\begin{array}{*{20}{l}} {7.9023,24.6841} \\ {6.0731,23.3232} \\ {4.6538,23.9501} \\ {6.2281,24.2653} \\ {5.5144,24.0229} \\ {5.0741,23.7246} \\ {7.4176,24.1417} \\ {7.5440,24.1781} \\ {7.3941,24.1429} \\ {12.500,29.3651} \end{array}} \right] 。$ | (23) |
船舶在整个航程的航行时间限定在120 h内,因此优化的总航行时间需满足:
| $ \sum\limits_{i = 1}^{10} {\frac{{{L_i}}}{{{V_{si}}}} \leqslant 120}。$ | (24) |
即:
| $ \begin{split} & \frac{{211.8}}{{{V_{s1}}}} + \frac{{99.3}}{{{V_{s2}}}} + \frac{{83.7}}{{{V_{s3}}}} + \frac{{117.5}}{{{V_{s4}}}} + \frac{{113.7}}{{{V_{s5}}}} + \frac{{230.5}}{{{V_{s6}}}}+ \\ & \frac{{195.1}}{{{V_{s7}}}} + \frac{{195.9}}{{{V_{s8}}}} + \frac{{129.5}}{{{V_{s9}}}} + \frac{{82.1}}{{{V_{s10}}}} \leqslant 120。\end{split} $ | (25) |
在上述分析的基础上,将不同航段对应主机转速、燃油消耗率、主机输出功率和航速上下限、时间上限输入编写好的人工蜂群算法程序中,经过优化计算即可得到对应航段的最优航速以及该航速下对应的主机油耗。
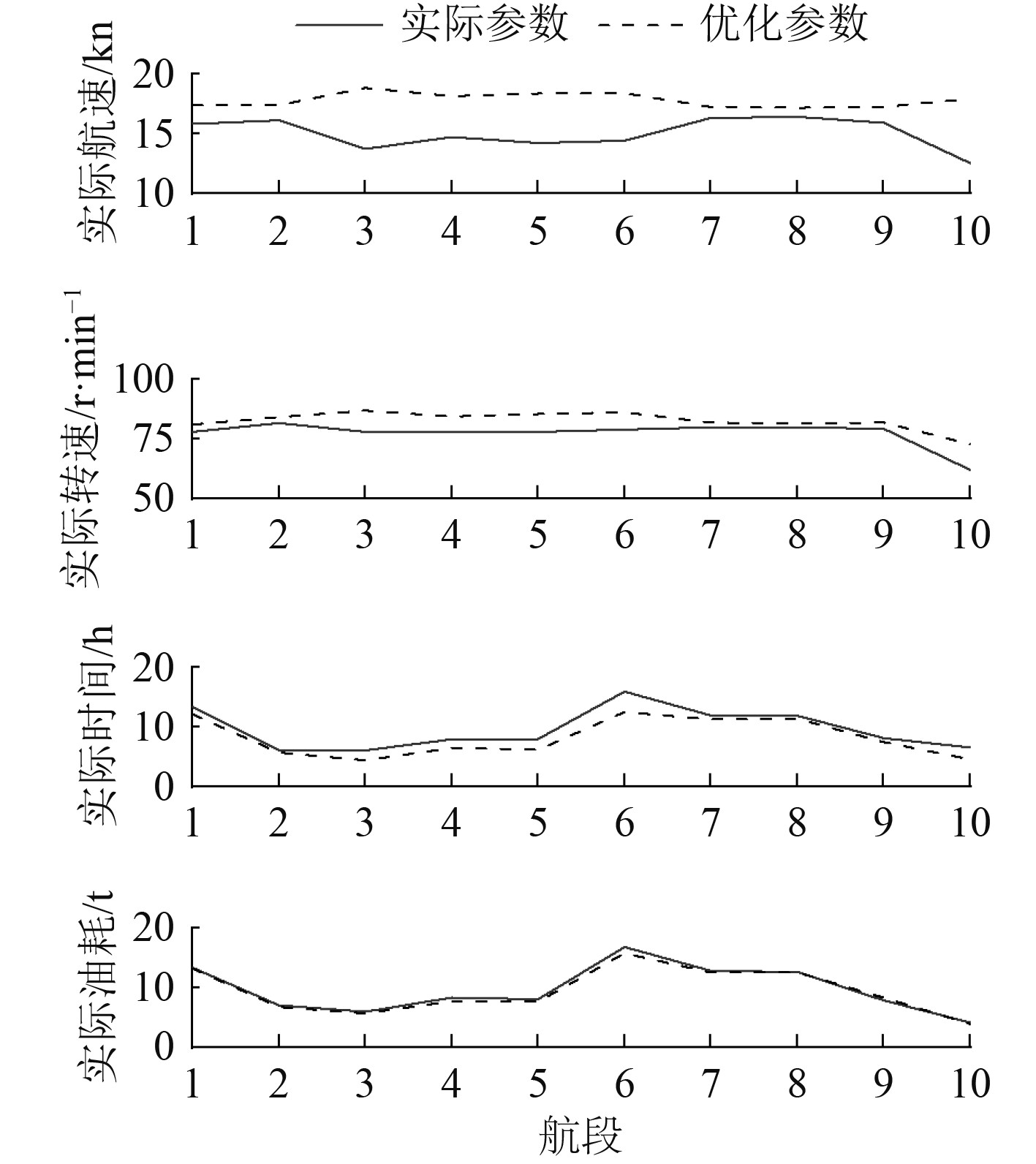
6 结果分析人工蜂群算法对船舶航速优化问题给出的最终优化结果见表4,优化前后航速、主机转速、航行时间、耗油量对比如图5所示。优化后的航速较优化前更快,节约了航行时间,这是航期内海浪、海风等海况条件较好影响的。
|
|
表 4 人工蜂群算法优化结果 Tab.4 Artificial bee colony algorithm optimization results |
|
图 5 优化前后参数对比 Fig. 5 Parameter comparison before and after optimization |
通过分析不难发现,优化后的航速较为平稳,便于在实际航行中实现,且略高于实际航速,降低了航行的成本。
7 结 语为研究航速优化与船舶油耗之间的关系,本文建立了比较贴合实际情况的油耗模型,并使用人工蜂群算法对航线实例进行航速优化。结果显示,经过优化后的,航行时间减少了14.44%,耗油量下降了3.012%。研究结果表明,使用人工蜂群算法对航速进行优化,降低船舶油耗,提高船舶能效水平。但是,在实际优化计算过程中,本文针对的是历史数据进行建模求解,距离船舶航行中实时提出航速建议还要考虑限速、航道拥堵和天气预报准确性等问题。
| [1] |
ZHU Guopiu, KWONG Sam. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation. 2020, 2017(7): 3166-3173. |
| [2] |
罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J]. 控制与决策, 2010, 25(12): 1913-1916.
|
| [3] |
毕晓君, 王艳娇. 加速收敛的人工蜂群算法[J]. 系统工程与电子技术, 2011, 33(12): 2755-2761. DOI:10.3969/j.issn.1001-506X.2011.12.34 |
| [4] |
LI Z, WANG W, YAN Y, et al. PS-ABC. A hybrid algorithm based on particle swarm and artificial bee colony for high-dimensional optimization problems[J]. Expert Systems with Applications, 2015, 42(22): 8881-8895. DOI:10.1016/j.eswa.2015.07.043 |
| [5] |
王志刚, 尚旭东, 夏慧明, 等. 多搜索策略协同进化的人工蜂群算法[J]. 控制与决策, 2018, 33(2): ;235-241. DOI:10.13195/j.kzyjc.2016.1597 |
| [6] |
CUI L, ZHANG K, LI G, et al. Modified G best-guided artificial bee colony algorithm with new probability model[J]. Soft Computing, 2018, 22(7): 2217-2243. DOI:10.1007/s00500-017-2485-y |
| [7] |
CHANG C C, CHANG C H. Energy conservation for international dry bulk carriers via vessel speed reduction[J]. Energy Policy, 2013, 59: 710-715. DOI:10.1016/j.enpol.2013.04.025 |
| [8] |
霍得利. 船舶航速优化节能性研究[D]. 大连, 大连海事大学, 2017.
|
| [9] |
范爱龙, 严新平, 尹奇志. 船舶主机能效模型[J]. 交通运输工程学报, 2015, 15(4): 69-76. DOI:10.19818/j.cnki.1671-1637.2015.04.009 |
| [10] |
马卫, 孙正兴. 基于精英蜂群搜索策略的人工蜂群算法[J]. 计算机应用, 2014, 34(8): 2299-2305. DOI:10.11772/j.issn.1001-9081.2014.08.2299 |
| [11] |
王圃, 郑成, 杨俊. 基于改进人工蜂群算法的供水泵站优化运行研究[J]. 给水排水, 2017, 53(6): 126-130. DOI:10.3969/j.issn.1002-8471.2017.06.029 |
| [12] |
刘伟, 周邵萍, 李长龙. 基于人工蜂群算法的矿山泵机组运行优化[J]. 流体机械, 2018, 46(1): 56-61. DOI:10.3969/j.issn.1005-0329.2018.01.012 |
| [13] |
张钊. 船舶运行状态检测与节能航速优化系统的研究与设计[D]. 武汉: 武汉理工大学, 2012.
|
| [14] |
张丽勇, 骆参驹. 海上航行数据特征的数据挖掘分析[J]. 舰船科学技术, 2016, 38(16): 76-78. |
 2023, Vol. 45
2023, Vol. 45
