船体结构在高速入水情况下,对周围流体介质产生冲击,同时流体也在自运行,在强大的冲击力下,尤其是在船体结构瞬态入水时,冲击力容易导致船体结构损坏或部分器件失灵情况[1],更严重时则会造成船体结构变形。船体结构高速入水过程涉及到船体结构、空气和水体三方的相互作用,船体结构高速入水时,会在水体内产生空气泡[2],该过程还涉及到气液相变过程,具有较强的耦合性和非线性。对于船体结构高速入水面临的问题,充分模拟船体高速入水冲击数值可为解决船体入水问题提供相应的数据分析基础。已有相关学者研究船体入水数值模拟方法,李鸿等[3]提出高速入水数值模拟方法,该方法利用MSC.Dytran软件建立船体三维模型,并设置不同高速入水速度对船体入水数值进行了仿真模拟。范旭东等[4]提出高速弹体入水冲击特性仿真方法,该方法利用ALE方式模拟高速弹体入水冲击过程,分析弹体入水特性以及压力和空泡演化过程。以上2种方法虽均可对船体结构高速入水过程进行数值仿真,但二者均存在仿真精度不足现象,因此应用效果不佳。流固耦合是流体力学和固体力学交叉形成的新力学分支,流固耦合是流体和固体介质之间的相互作用,该种作用可改变流体的荷载分布以及荷载大小。而船体结构高速入水时,其具有极强的流固耦合性,在研究船体结构冲击数值仿真时,需要考虑其流固耦合性[5]。为此提出流固耦合分析下的船体高速入水冲击数值模拟方法,为船体高速入水冲击研究提供有效技术手段。
1 船体高速入水冲击数值模拟方法 1.1 基于ALE的流固耦合分析方法任意拉格朗日欧拉米德(ALE)方法是连续介质力学的一种描述方法,该方法可描述物质变形状态。在此以ALE方法对船体结构高速入水时产生的冲击进行流固耦合分析,其详细过程如下:
| $ \frac{{\partial {\rho _w}}}{{\partial t}} + {c_i}\frac{{\partial {\rho _w}}}{{\partial {g_i}}} + {\rho _w}\frac{{\partial {z_i}}}{{\partial {g_i}}} = 0 ,$ | (1) |
| $ {c_i} = {v_i} - {w_i} 。$ | (2) |
式中:
令
| $ {\rho _w}\left[ {\frac{{\partial {z_i}}}{{\partial t}} + {c_i}\frac{{\partial {z_i}}}{{\partial {g_j}}}} \right] = {\varphi _{ij}} + {\rho _w}{\eta _i} 。$ | (3) |
式中:
| $ {\varphi _{ij}} = - {Q_s}{\delta _{ij}} + {\mu _d}{z_{ij}} + {\mu _d}{z_{ji}} 。$ | (4) |
式中:
在使用ALE结合有限元方法分析船体结构冲击数值时,固体结构和流体之间的界面是通过流体体积函数获取的[6],但固体结构高速入水的角度和速度受有限元网格密度影响较大,在使用有限元对船体结构入水进行仿真模拟时,需要计算其流固耦合罚函数。流固耦合罚函数计算方法与弹簧系统类似。弹簧系统的流固耦合罚函数合理是通过弹簧刚度和穿透深度比例计算的[7],因此船体结构在高速入水时的罚函数耦合力计算公式如下:
| $ M = \psi d。$ | (5) |
式中:
对于船体结构高速下水时的弹簧刚度数值
| $ \psi = \varepsilon rE \cdot \frac{1}{V} 。$ | (6) |
式中:
经过上述步骤,可获得船体高速入水时的质量守恒和动量守恒情况,并可通过罚函数获得较佳的有限元模型网格密度,依据罚函数数值,建立船体结构有限元模型。
1.2 船体有限元数值仿真模型构建为简化船体高速入水冲击数值模拟过程,将船体结构看做圆筒形,圆筒半径为45 mm,高度为95 mm,厚度为2.5 mm,其入水高度为20 m。依据罚函数数值,在有限元软基内使用Lagrange格式4节点四边形的单元壳,划分圆筒网格,并依据船体结构材料,使用有限元软件内MATRIG定义圆筒结构的材料属性后,得到圆筒结构有限元模型,该模型如图1所示。
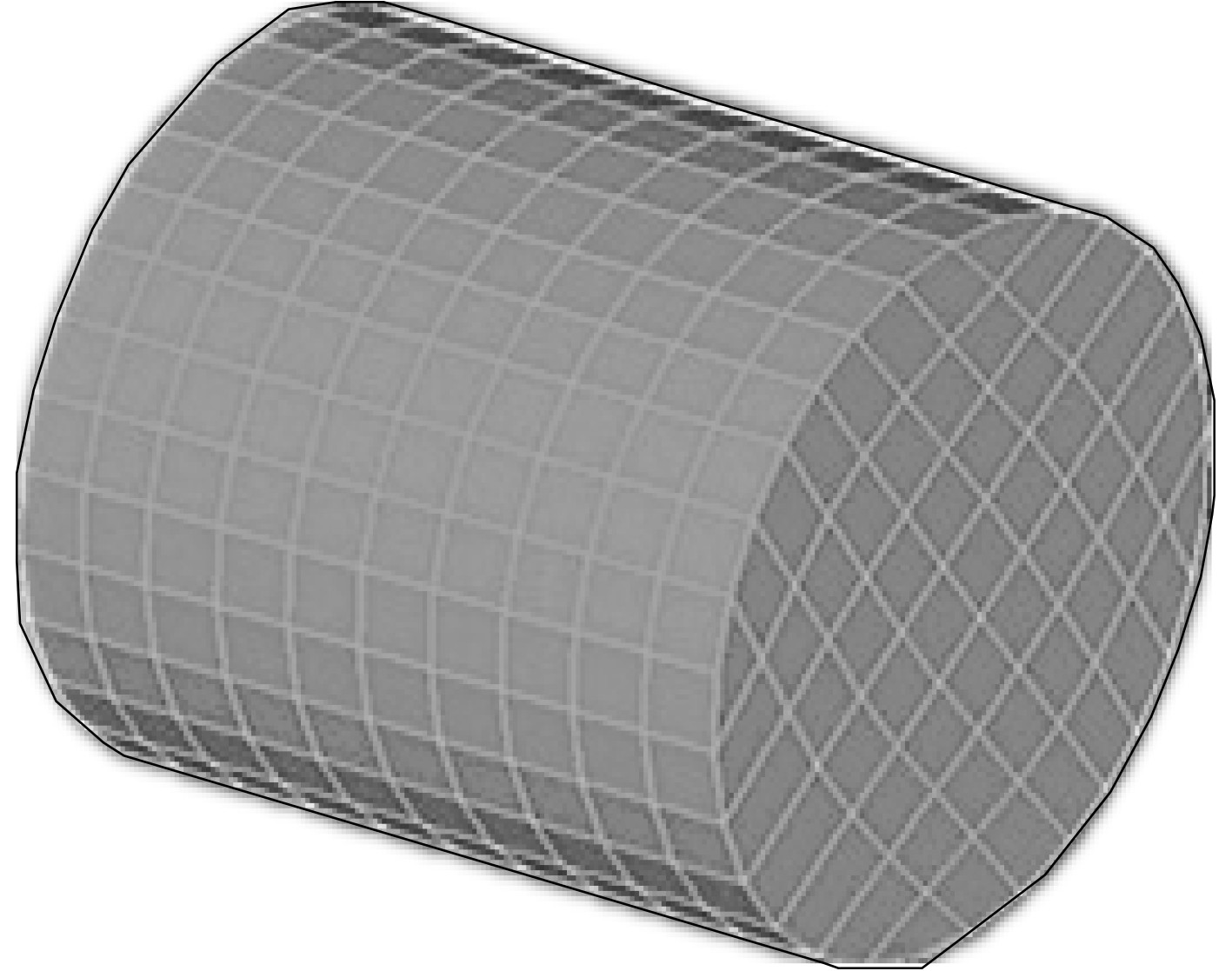
|
图 1 船体简化后圆筒结构有限元模型 Fig. 1 Finite element model of simplified cylindrical structure of ship hull |
船体结构高速入水时,流体为空气和水,使用有限元建立流体域时,将其划分为上下2个部分,上部为空气介质,下部为水介质,上下两部分尺寸为300 mm×300 mm×60 mm。流体域网格共有12632个Euler单元,使用可压缩理想气体材料填充流体域上部分。则流体域的空气压力表达公式如下:
| $ P = (\gamma - 1)\rho e 。$ | (7) |
式中:
流体域下层为水介质,其尺寸为300 mm×300 mm×280 mm,划分为34509个Euler单元,使用可压缩线性流体材料填充单元。则在流体区域内,
| $ P' = {h_1}\mu + {h_2}{\mu ^2} + {h_3}{\mu ^3} + {\rho _0}e'{f_0} + {\rho _0}e'{f_1}\mu ,$ | (8) |
| $ \mu = \frac{{\rho '}}{{{\rho _0}}} - 1 。$ | (9) |
式中:
当水处于拉伸状态时,
| $ P' = {h_1}\mu + {f_0}{\rho _0}e' + {f_1}\mu {\rho _0}e'。$ | (10) |
结合流体域,建立的船体结构高速入水有限元仿真模型如图2所示。
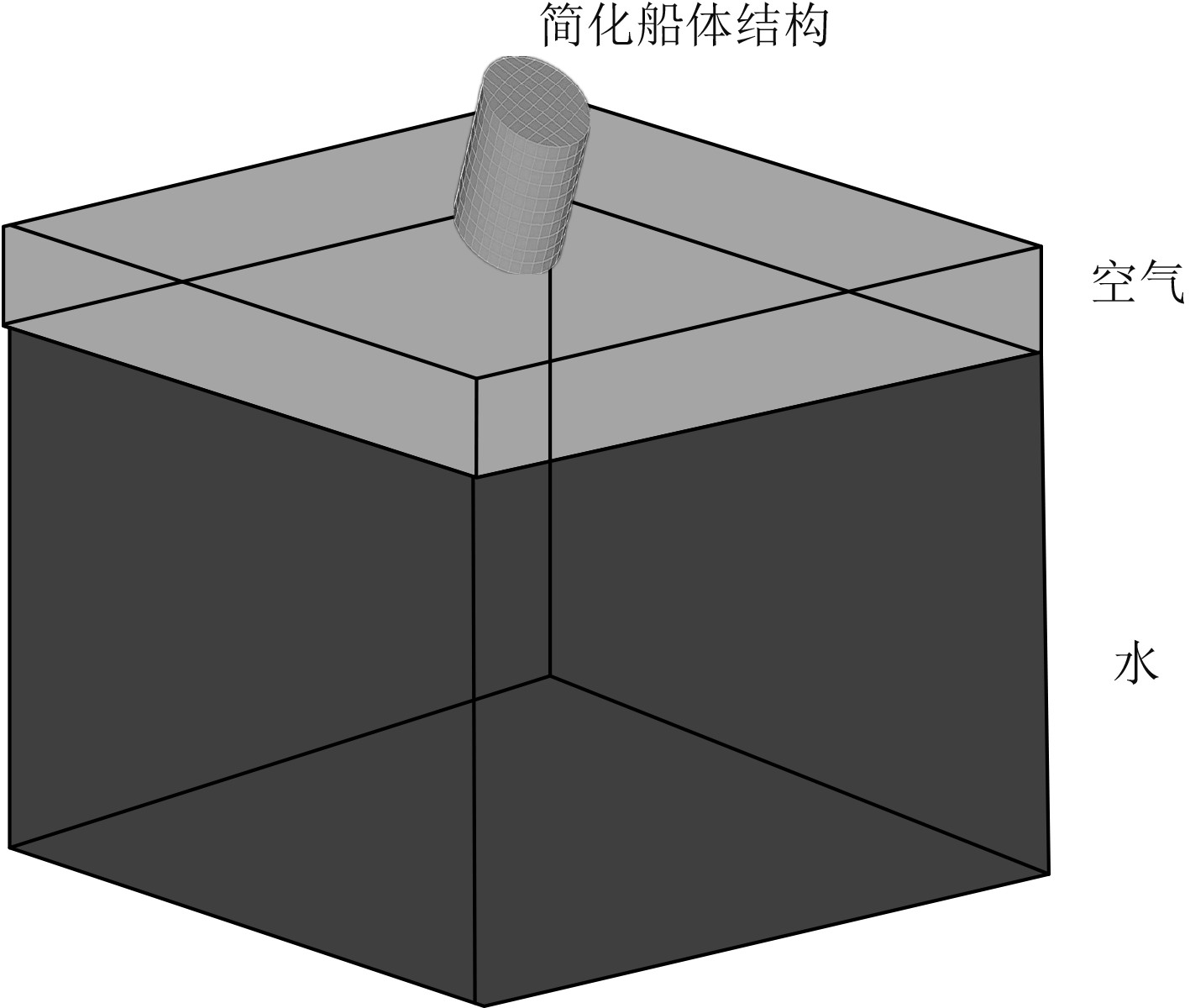
|
图 2 船结构高速入水有限元仿真模型 Fig. 2 Finite element simulation model of ship structure entering water at high speed |
考虑到船体结构高速入水时水介质起到的气垫作用,在数值仿真模拟时,船体结构表面定义成耦合面,在船体结构仿真模型网格内,其流体可自由流动。
2 性能测试与分析利用建立好的船体结构高速入水仿真有限元模型,对船体入水时的冲击数值展开模拟,验证本文方法实际应用效果。
利用船体结构高速入水仿真有限元模型模拟船体结构高速入水时,流固耦合状态下水介质飞溅和超空泡情况,船体结构入水速度设置为20 m/s,模拟结果如图3所示。分析可知,当船体结构高速入水初期,船体结构撞水瞬间产生的巨大加速度会迅速传递到船体结构上,但由于船体结构无法瞬时完全吸纳冲击力,导致船体结构高速入水时撞击水面将水排开,而水介质在船体结构入水时呈现水平面上升和水花飞溅现象,且在船体结构入水后,在水中形成了对称的超空泡,此时空气与水介质呈现流固耦合状态。

|
图 3 流固耦合状态下水介质飞溅和超空泡情况 Fig. 3 Splash and supercavitation of water medium in fluid solid coupling state |
以船体结构高速入水时的加速度作为指标,模拟在流固耦合状态下,船体结构撞击水面瞬间的加速度变化情况,结果如图4所示。分析可知,船体结构从高处以较快的速度入水时,船体结构与水面具有一定距离,船体结构会在空气中停留一段时间,在该时间段内,船体结构底部位置和水介质之间的空气会向四周逃逸,此时船体结构的加速度数值略小,该阶段也被称为气体压缩阶段。当船体结构接触到水面时,在船体结构高速入水的瞬间,其承受的冲击荷载最大,使其加速度曲线呈直线上升趋势,同时船体结构在自身重力和水、空气压力作用下,加速度曲线随着时间增加呈现迅速下降状态,该过程水介质产生扰动,出现飞溅效应,该阶段为液体运动阶段,因此在时间为0.04 s左右时,船体结构的加速度冲击响应曲线受空气和水介质耦合作用,产生波动。当船体结构持续入水时,其加速度受到水阻力呈现为0状态,但当船体结构弹性较大时,其容易出现负压现象。
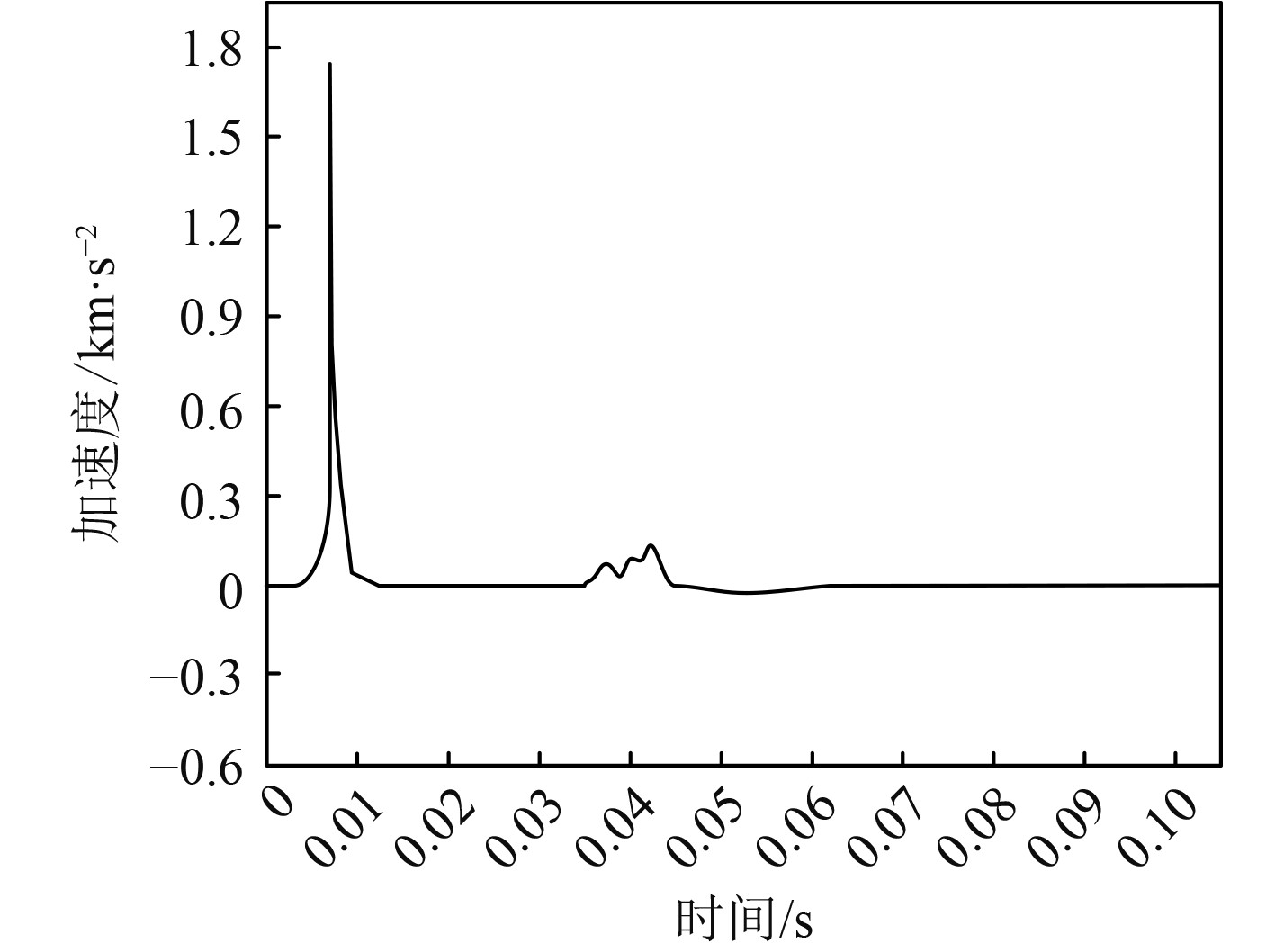
|
图 4 加速度冲击响应曲线 Fig. 4 Acceleration impact response curve |
以Y方向船体结构应力变化为分析目标,模拟船体结构高速入水后,其Y方向应力变化情况并绘制曲线,结果如图5所示。分析可知,在船体结构高速入水的瞬间,船体结构碰击水面后,船体和水介质之间碰撞持续时间较短,但瞬时产生的冲击力较大,冲击力迅速在船体结构内传播。船体结构在入水时间为1 ms左右时,其结构应力达到−150 MPa左右,随着船体结构持续入水,其水平方向的冲击波在船体结构与水面不断接触过程中产生震荡情况,结构应力也随之震荡,但结构应力始终在0 MPa左右震荡,震荡数值较小。
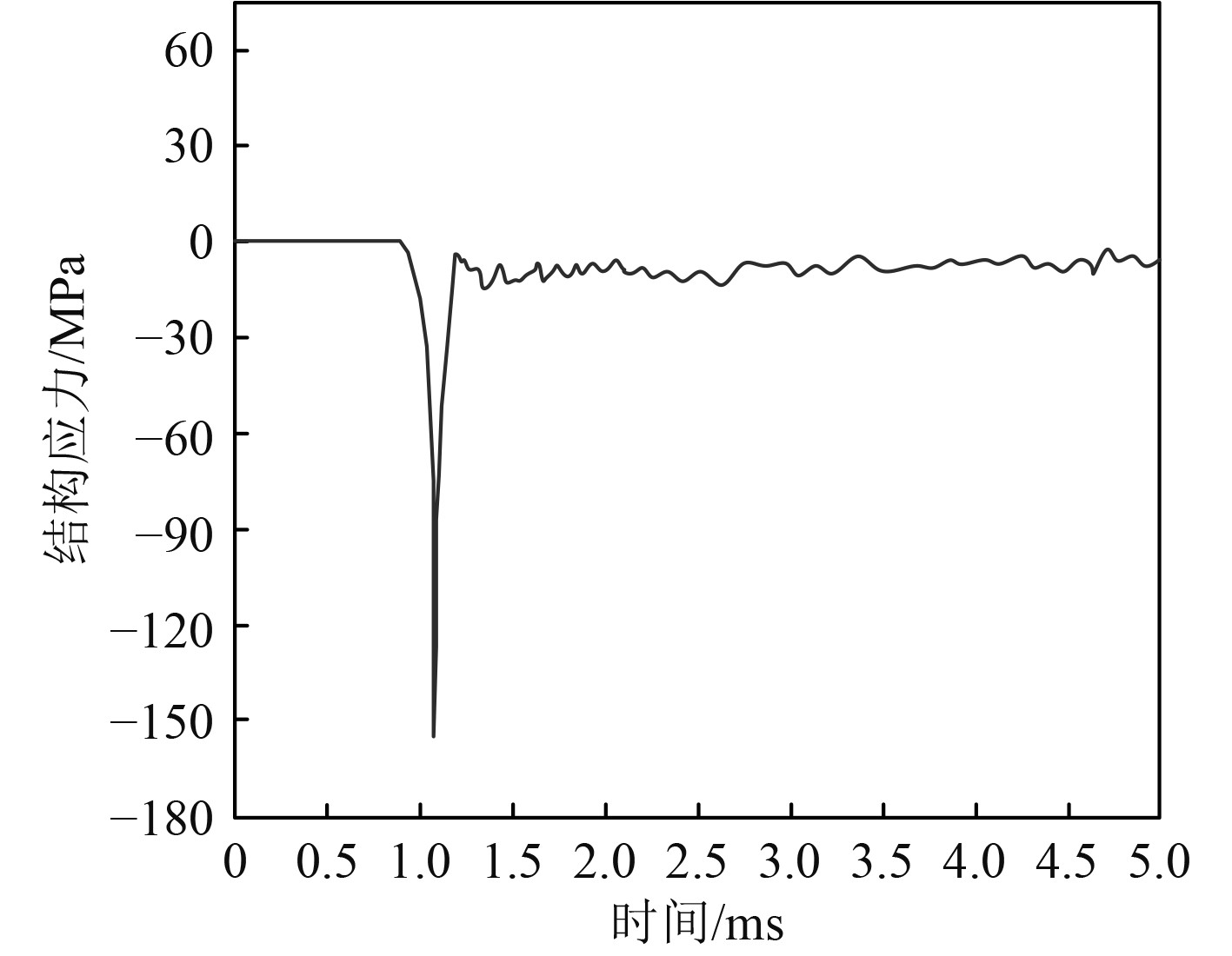
|
图 5 船体结构应力变化曲线 Fig. 5 Stress change curve of hull structure |
本文研究流固耦合分析下的船体高速入水冲击数值模拟方法,通过有限元软件建立简化的船体结构模型并对其进行高速入水冲击仿真。从仿真结果可知,船体结构入水瞬间加速度数值和船体结构应力变化均较大,随着时间增加,船体结构的加速度和结构应力在流固耦合状态下的数值均呈现下降趋势。
| [1] |
刘云龙, 王平平, 王诗平, 等. 水下爆炸作用下舰船冲击毁伤的瞬态流固耦合FSLAB软件数值模拟分析[J]. 中国舰船研究, 2022, 17(5): 228-240. LIU Yun-long, WANG Ping-ping, WANG Shi-ping, et al. Numerical analysis of transient fluid-structure interaction of warship impact damage caused by underwater explosion using the FSLAB[J]. Chinese Journal of Ship Research, 2022, 17(5): 228-240. |
| [2] |
王平平, 张阿漫, 彭玉祥, 等. 近场水下爆炸瞬态强非线性流固耦合无网格数值模拟研究[J]. 力学学报, 2022, 54(8): 2194-2209. WANG Ping-ping, ZHANG A-man, PENG Yu-xiang, et al. Umerical simulation of transient strongly-nonlinearn flutd-structure interaction in near-field underwater explosion based on meshless meshless method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(8): 2194-2209. |
| [3] |
李鸿, 李光磊, 刘志远, 等. 基于流固耦合的降载空化器高速入水数值研究[J]. 振动与冲击, 2021, 40(23): 254-259. LI Hong, LI Guang-lei, LIU Zhi-yuan, et al. Numerical simulation of high-speed water entry of cavitator with load reduction device based on fluid-structure interaction[J]. Journal of Vibration and Shock, 2021, 40(23): 254-259. |
| [4] |
范旭东, 漆超, 王旭, 等. 基于ALE方法的高速弹体入水冲击特性研究[J]. 江苏科技大学学报(自然科学版), 2022, 36(2): 7-14. FAN Xu-dong, QI Chao, WANG Xu, et al. Research on water impact characteristics of high-speed projectiles based on ALE method[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2022, 36(2): 7-14. |
| [5] |
郝常乐, 党建军, 陈长盛, 等. 基于双向流固耦合的超空泡射弹入水研究[J]. 力学学报, 2022, 54(3): 678-687. HAO Chang-le, DANG Jian-jun, CHEN Chang-sheng, et al. Research on supercavitation projectile entering water based on bidirectional fluid solid coupling[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 678-687. |
| [6] |
王得辰, 张俊婷, 樊佳伟. 载瘤动脉双向流固耦合动力学数值模拟分析[J]. 中北大学学报(自然科学版), 2023, 44(1): 16-23. WANG De-chen, HANG Jun-ting, FAN Jia-wei. Numerical Simulation on bidirectional fluid-structure interaction kinetics of the Parent Artery[J]. Journal of North University of China(Natural Science Edition), 2023, 44(1): 16-23. |
| [7] |
肖睿, 魏继锋, 吉耿杰, 等. 前抛体对弹体入水载荷影响数值模拟研究[J]. 爆炸与冲击, 2023, 43(4): 64-77. |
 2023, Vol. 45
2023, Vol. 45
