阻尼是结构动力分析的基本参数,对动力分析结果的可信性和精度有很大影响;但阻尼的产生机理和影响因素复杂,目前最常用也是比较简单的阻尼是瑞利阻尼,又称比例阻尼。它是多数实用动力分析的首选,能满足实际工程应用精度的需求,但瑞利阻尼系数的确定[1-3]存在一定困难。浮筏是目前应用最为广泛的隔振系统,其结构较为复杂,阻尼是影响浮筏动力特性分析准确性的重要因素之一。因此,准确计算得到浮筏的瑞利阻尼系数相当重要。
本文首先结合瑞利阻尼的物理意义,在模态阻尼比已知的前提下,利用加权最小二乘法计算瑞利阻尼系数,使得各阶模态阻尼比相对误差的平方和最小;然后结合模态分析提出了累计有效质量参与系数高于95%的模态选取原则。算例表明,结合该模态选取原则,利用加权最小二乘法计算得到的瑞利系数能满足浮筏工程计算中的实际需要。
1 瑞利阻尼介绍实际工程应用中广泛使用的是粘滞阻尼。粘滞阻尼假定阻尼力大小与运动速度成正比,方向与速度相反[4]。
在单自由度系统中阻尼力可表示为:
| $ f = c\dot u = j{\omega _n}cu 。$ | (1) |
式中:f 为阻尼力;c 为系统阻尼;u 为结构位移;ωn为激励力频率。
阻尼比ξ并非是恒定值,与频率有一定的对应关系:
| $ \xi = \frac{c}{{{c_{cr}}}} = \frac{c}{{2m{\omega _0}}} = \frac{c}{{2\sqrt {km} }} 。$ | (2) |
式中:ccr为单自由度系统的阻尼临界值;k为结构刚度;m为结构质量;ω0为系统不考虑阻尼时的自振频率。
对多自由度系统粘滞阻尼而言,与单自由度阻尼力相对应,其可用向量形式表达:
| $ {{F_d}} = {\boldsymbol{C}}{\dot u} 。$ | (3) |
式中:Fd为阻尼力列向量;C为等效粘滞阻尼矩阵;
根据阻尼矩阵C是否可以通过模态向量正交化为对角矩阵,将其分为正交阻尼和非正交阻尼。瑞利阻尼模型是广泛采用的一种正交阻尼模型,其表达式为[5]:
| $ {\boldsymbol{C}} = \alpha {\boldsymbol{M}} + \beta {\boldsymbol{K}}。$ | (4) |
其中:M为系统的质量矩阵;K为刚度矩阵;α、β分别为系统的质量阻尼乘子、刚度阻尼乘子。式(4)表明在瑞利阻尼中,阻尼矩阵是质量矩阵和刚度矩阵的线性叠加,且3个矩阵均为对角阵。
根据有限元基础理论可知,有限元分析时简谐力作用下系统的运动方程为[6]:
| $ {\boldsymbol{M}}{\ddot u(t)} + {\boldsymbol{C}} {\dot u(t)} + {\boldsymbol{K}} {u(t)} = {f(t)}。$ | (5) |
式中:u(t)、
通过正交变换,式(5)可变换为:
| $ { {\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{M}} {\boldsymbol{\phi}}{\ddot \xi } + { {\boldsymbol{\phi}} ^T}{\boldsymbol{C}} {\boldsymbol{\phi }} {\dot \xi } +{{\boldsymbol{\phi}} ^{\rm{T}}}K {\boldsymbol{\phi }} \xi = { {\boldsymbol{\phi}} ^{\rm{T}}}f(t)。$ | (6) |
式中:
| $ \left\{ {{{\ddot \xi }_j}} \right\} + 2{\zeta _j}{\omega _j}\left\{ {{{\dot \xi }_j}} \right\} + \omega _j^2\left\{ {{\xi _j}} \right\} = \left\{ {{f_j}(t)} \right\}。$ | (7) |
式中:ζj为第j阶模态阻尼比;ωj为j阶模态频率;fj(t)为模态坐标系下第j阶振型所对应的激振力。
结合式(4)得到:
| $ {{\boldsymbol{\phi}} ^{\rm{T}}}{\boldsymbol{C}} {\boldsymbol{\phi}} = \left( {\begin{array}{*{20}{c}} {\alpha + \beta \omega _1^2}& \cdots &0 \\ \vdots & \ddots & \vdots \\ 0& \cdots &{\alpha + \beta \omega _n^2} \end{array}} \right)。$ | (8) |
由对称性可推得:
| $ 2{\zeta _i}{\omega _i} = \alpha + \beta \omega _i^2。$ | (9) |
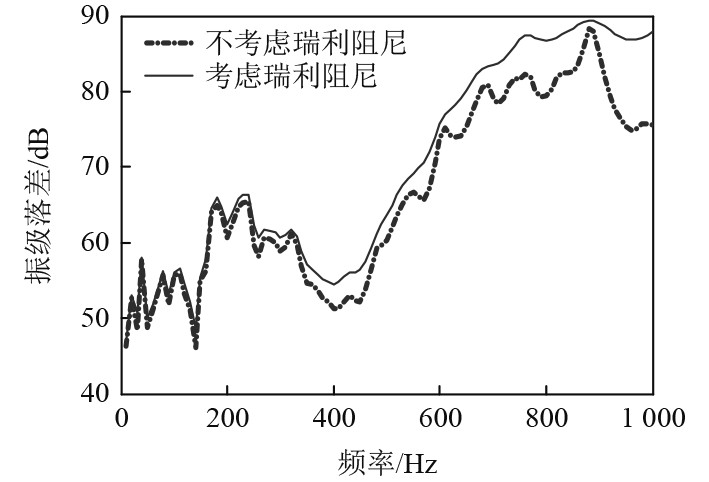
比较考虑瑞利阻尼和不考虑瑞利阻尼时某浮筏的隔振效果,如图1所示。可知,在频率低于200 Hz,时瑞利阻尼对隔振效果的影响并不明显,但在中高频段尤其是当频率高于700 Hz时,瑞利阻尼的作用得以体现,除880~900 Hz外,振级落差的差别均大于5 dB,在930~1 000 Hz内差别大于10 dB。因此瑞利阻尼在高频段对浮筏隔振效果的影响较为明显,所以准确且合理确定瑞利阻尼系数非常重要。
|
图 1 瑞利阻尼对隔振效果的影响 Fig. 1 Influence of Rayleigh damping on vibration isolation effect |
在结构动力特性仿真过程中,为真实反映结构的阻尼特征,一般是根据实验测试或现有数据,选取前m阶(m
目前,应用最为普遍的方法是根据2个不等的模态频率及其所对应的模态阻尼比确定阻尼系数,即
| $ a = \frac{{2\left( {{\zeta _j}{\omega _i} - {\zeta _i}{\omega _j}} \right){\omega _i}{\omega _j}}}{{\omega _i^2 - \omega _j^2}},$ | (10) |
| $ \beta = \frac{{2\left( {{\zeta _i}{\omega _i} - {\zeta _j}{\omega _j}} \right)}}{{\omega _i^2 - \omega _j^2}} 。$ | (11) |
一般选取对结构动力特性影响最大的两阶模态或者分析时的第一阶和最后一阶模态。该方法操作简单,但仅能反映少数几阶模态的阻尼特性,在宽频带范围内效果较差。
2.1 加权最小二乘法计算瑞利阻尼系数如果系统自由度较大,利用上述方法得到的阻尼系数计算相应模态阻尼比,计算结果同要求值相差较大。结合误差理论,利用加权最小二乘法,使得各阶模态所对应的模态阻尼比相对误差的平方和最小[7],该方法在较宽频带内能够反映多数阶次模态的阻尼特性。
加权最小二乘法的基本思想是通过对原模型加权,使之变成一个新的不存在异方差性的模型,然后采用普通最小二乘法估计其参数。
理论上最优权数wi为误差项方差σi2的倒数,即
| $ {w_i} = 1/\sigma _i^2 。$ | (12) |
误差项方差大的项接受小的权数,以降低其在平方和中的作用;误差项方差小的项接受大的权数,以提高其在平方和中的作用[8]。
设第
| $ {e_i} = \left| {\frac{{{\zeta _{\rm{iinput}}} - {\zeta _{\rm{irequest}}}}}{{{\zeta _{\rm{irequest}}}}}} \right|。$ | (13) |
式中:ζirequest为结构所要求的阻尼比或实测值;ζiinput为结构分析动力响应方程所具有的真实阻尼比,由式(9)确定。设权值为wi,则加权平方和E为:
| $ E = \sum\limits_{i = 1}^n {{w_i}} e_i^2。$ | (14) |
将式(13)代入式(14)得到:
| $ E = \sum\limits_{i = 1}^n {{w_i}} \left(\frac{{\alpha + \beta \omega _i^2}}{{2{\omega _i}{\zeta _i}}} - 1\right)。$ | (15) |
将式(15)分别对α和β求偏导并令偏导为0,得
| $ a = \frac{{2\left[ {\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{{\omega _i}{\zeta _i}}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}\omega _i^2}}{{\zeta _i^2}}} } - \displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}\omega {}_i}}{{{\zeta _i}}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}} } } \right]}}{{\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}\omega _i^2}}{{\zeta _i^2}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\omega _i^2\zeta _i^2}}} } - \displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}} } }},$ | (16) |
| $ \beta = \frac{{2\left[ {\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}{\omega _i}}}{{{\zeta _i}}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\omega _i^2\zeta _i^2}}} } - \displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\omega {}_i{\zeta _i}}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}} } } \right]}}{{\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}\omega _i^2}}{{\zeta _i^2}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\omega _i^2\zeta _i^2}}} } - \displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}\displaystyle\sum\limits_{i = 1}^n {\frac{{{w_i}}}{{\zeta _i^2}}} } }}。$ | (17) |
首先分别利用2种方法计算瑞利阻尼系数,比较各阶模态阻尼比的相对误差。模拟对象为一梁结构,试验测得其对应模态频率和模态阻尼比见表1[9]。利用瑞利阻尼系数计算得到结构动力分析时的真实阻尼比,以各阶模态阻尼比的相对误差为比较对象,结果如表2所示。
|
|
表 1 梁结构前七阶模态频率与模态阻尼比 Tab.1 The first seven modal frequencies and modal damping ratio of a beam structure |
|
|
表 2 不同计算方法对应结果比较图 Tab.2 Compares the corresponding results of different calculation methods |
由表2可知,利用加权最小二乘法计算得到的绝大部分阶次模态阻尼比的相对误差较通用方法有所减小,证实了该方法的有效性。
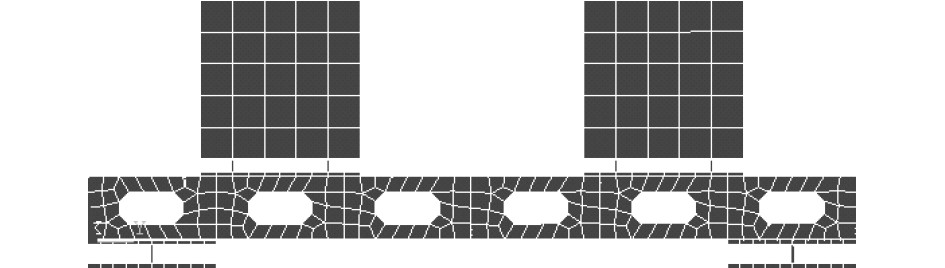
3 浮筏瑞利阻尼系数的确定浮筏是由设备、筏架、基座、上下层隔振器组成的复杂隔振系统。以某艇用浮筏为计算对象,有限元模型如图2所示。浮筏上安装有2台设备,筏架长3.5 m,宽1.8 m,高0.4 m,基座以钢板模拟,上下层隔振器阻尼比均为0.09。
|
图 2 浮筏有限元模型 Fig. 2 Finite element model of floating raft |
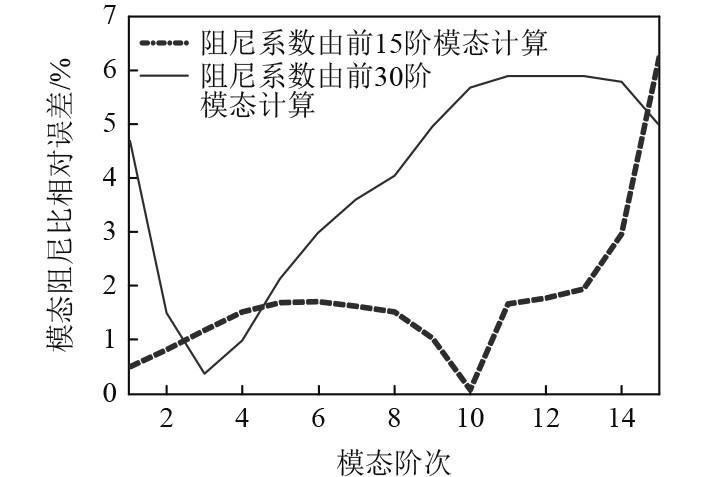
依据各阶模态阻尼比,利用加权最小二乘法计算浮筏的瑞利阻尼系数虽然可行,但参与计算的模态数越多,效果越差。图3比较了利用前15阶模态参数和前30阶模态参数计算瑞利阻尼系数,所对应的前15阶模态阻尼比的(假设模态阻尼比为恒定值0.02)相对误差。
|
图 3 前15阶模态阻尼比的相对误差 Fig. 3 Relative errors of the first 15 modal damping ratios |
由图3可知,若模态阶数选的过少,高阶模态对应的模态阻尼比的相对误差较大;模态阶数选的过多几乎所有参与计算的模态阻尼比相对误差都会增加。因此合理选取参与计算的模态阶数不仅可使分析结果合理可靠,还可节约时间和存储空间。
3.1 模态选择方法振动的广义特征值问题[10]为:
| $ ({\boldsymbol{K}} -{\omega ^{\text{2}}}{\boldsymbol{M}})\phi = \phi。$ | (18) |
计算结构的模态时,采用集中质量,并将模态进行标准化处理:
| $ \phi _j^{\rm{T}}{\boldsymbol{M}}{ \phi _j} = 1。$ | (19) |
式中:
| $ {F_{ji}} = \phi _{ji}^{\rm{T}}{\boldsymbol{M}}{ {\boldsymbol{D}} _j}。$ | (20) |
式中:i为模态阶数;j为作用力方向,每阶模态可能各有
第i阶模态第j方向的有效模态质量定义为:
| $ {M_{ji}} = \frac{{F_{ji}^2}}{{\phi _j^{\rm{T}}{\boldsymbol{M}}{{ \phi }_j}}}。$ | (21) |
相应的j方向累计有效模态质量参与系数
| $ {r_j} = \frac{{\displaystyle\sum\limits_{i = 1}^m {{M_{ji}}} }}{{{M_{\rm{total}}}}}。$ | (22) |
式中:Mtotal为结构总质量,由式(19)知Mji=Fji2,此外所有阶模态有效模态质量之和等于结构总质量。
由于模态有效质量考虑了振型参与因子,可反映相应模态在动力反应中的参与度,因此能够作为模态选取的主要判据[9-10]。
浮筏作为复杂隔振系统,其各阶模态参数反映相应的动力学特性,并且高阶模态对其动力学特性影响很小,当分析的模态阶数满足主自由度方向(在平动自由度中选取)的有效模态质量超过总质量的95%时,即认为分析满足要求。从该点出发,提取rj=0.95之前的所有模态的模态参数,利用模态频率与模态阻尼比求取瑞利阻尼系数。
3.2 浮筏瑞利阻尼系数的确定假设浮筏各阶模态阻尼比为定值0.02,提取的3个平动方向的前100阶模态参数,模型总质量为3077 kg,其前100阶X、Y、Z方向的有效模态质量之和分别为2715.4 kg、2840 kg、2958 kg,可知Z为主自由度方向。表3为部分阶次模态的相关数据。
|
|
表 3 Z方向部分阶次模态参数 Tab.3 Partial order modal parameters in the Z direction |
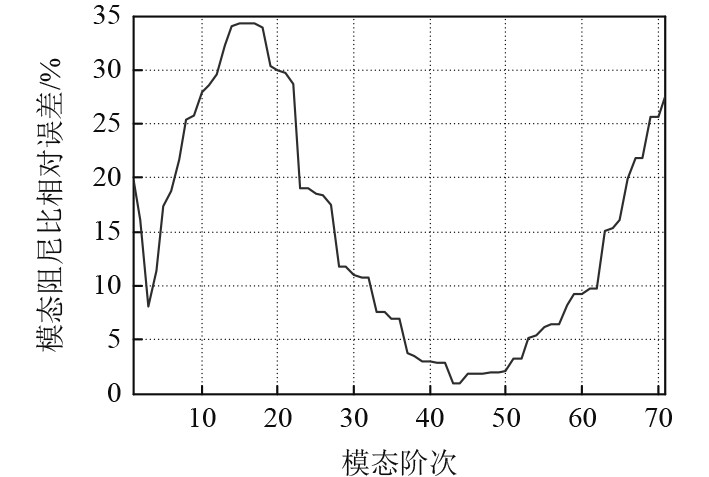
可知,前71阶模态的累计有效质量参与系数已超过总质量的95%。取前71阶模态所对应的模态阻尼比计算瑞利阻尼系数,得到α=2.504,β=3.55×10−5。计算得到的模态阻尼比与要求值的相对误差如图4所示。
|
图 4 模态阻尼比相对误差 Fig. 4 Relative error of modal damping ratio |
可知:在前71阶模态中,7~22及66~71阶模态阻尼比的相对误差超过20%,其余均在20%之内。从瑞利阻尼系数对浮筏隔振性能影响的角度可知,利用加权最小二乘法计算阻尼系数能够满足实际工程需要。
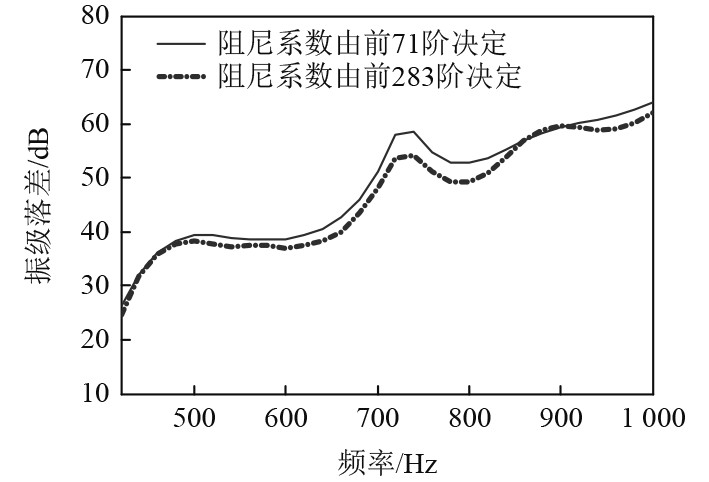
此外,结合研究频段0~1 000 Hz内的所有模态频率(共283阶)并假设模态阻尼比均为0.02,利用加权最小二乘法计算对应的瑞利阻尼系数,得到α=3.3,β=183×10−5。依次利用前71阶模态参数确定的阻尼系数和利用前283阶模态参数确定的阻尼系数计算浮筏的隔振效果,计算频率限于71~283阶模态对应的频率段,如图5所示。
|
图 5 不同阻尼系数对应的隔振效果 Fig. 5 Vibration isolation effect corresponding to different damping coefficients |
可知,利用低频段的模态频率计算瑞利阻尼系数依然适用于高频,浮筏隔振效果的计算误差最大不超过4 dB,这说明依据主自由度有效模态质量累计参与系数高于95% 的模态选取原则确定的瑞利阻尼系数,是满足不同频段计算需求的。
4 结 语本文详细介绍了瑞利阻尼和加权最小二乘法,并从模态阻尼比相对误差的平方和最小为出发点,利用加权最小二乘法计算瑞利阻尼系数。将计算结果同常用方法相比较,证明了加权最小二乘法的有效性。
针对浮筏等复杂结构,结合基于有效模态质量参与系数的模态分析方法确定了rj≥95%的模态选取原则,并将该方法用于浮筏动力特性分析时瑞利阻尼系数的确定。计算得到动力分析时,模态阻尼比的真实值与要求值相对误差在少部分阶次模态超过20%,大部分阶次的模态阻尼比相对误差不超过20%,能满足浮筏动力特性计算的工程实际需要。
| [1] |
TAO J C, MAK C M. Effect of viscous damping on power transmissibility for the vibration isolation of building services equipment[J]. Applied Acoustic, 2006(67): 733-742. |
| [2] |
傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000.
|
| [3] |
TROMBETTI T, SILVERTRI S. On the modal damping ratios of shear-type structure equipped with Raileigh damping systems[J]. Journal of Sound and Vibration. 2006(292): 21-58.
|
| [4] |
付建, 王永生, 魏应三. 阻尼对浮筏隔振性能的影响研究[J]. 船海工程, 2011, 40(3): 169-172. DOI:10.3963/j.issn.1671-7953.2011.03.047 |
| [5] |
CAI C H, ZHENG M, KHAN M S, etal. Modeling of material damping properties in ansys[C]// 2002 CADFEM Users’ Meeting & Ansys Conference. Friedrichshafen, Germany, 2002.
|
| [6] |
王淮峰, 楼梦麟, 张如林. 加权最小二乘法求解Rayleigh阻尼系数的讨论[J]. 计算力学学报, 2017, 34(5): 603-607. |
| [7] |
KANDEG G M, Influence of mode dependent rayleigh damping on transient stress response[D]. Karlskrona: Blekings Institute of Technology, 2007.
|
| [8] |
郑毅. 结构比例阻尼和复模态阵型复杂度的参数研究[D]. 大连: 大连理工大学, 2018.
|
| [9] |
INDRAJIT C, SHAMBHM P D. Computation of rayleigh damping coefficients for large systems[J]. The Electronic Journal of Geotechnical Engineering, 2003(8): 114-123. |
| [10] |
侯晓武, 杨志勇, 王莹. 不同阻尼模型对动力弹塑性分析响应影响分析[J]. 建筑科学, 2020(S2): 254-258. |
 2023, Vol. 45
2023, Vol. 45
