2. 黑龙江水运规划设计院有限公司,黑龙江 哈尔滨 150000
2. Heilongjiang Water Transport Planning and Design Institute Co., Ltd., Harbin 150001, China
拖曳式多参数剖面测量系统又称为水下拖曳系统,目前作为水下探测装置广泛应用在海洋研究及监测和军事等领域,其在海洋环境、海洋资源调查和国防建设中均有非常重要的用途[1]。现今的拖曳系统包括航速较低的拖曳系统,又或是系泊拖曳状态下的拖曳系统,而高速拖曳技术目前来说刚刚起步,美国提出了OASIS系统[2],该系统搭载平台为MH-60S直升机,为直升机拖曳系统。而滑行艇作为水面高速船,在续航力、操纵性以及载重量上,均优于直升机,且船上的观测点与探测点的距离较直升机更短,在实时监控以及数据传输上优势更大。
滑行艇在高速航行遇到波浪时,会在波浪中颠簸并发生砰击[3]。截至目前,对滑行艇在静水与迎浪规则波中航行的阻力性能及运动响应的预报技术主要为数值模拟和模型试验,而滑行艇的模型试验技术相对更加成熟。梁霄等[4]利用Fluent对滑行艇的直航运动进行数值模拟计算与验证;凌杰[5]通过FINE/Marine对滑行艇在规则波中的自航进行了值预报;凌宏杰等[6]采用随体网格技术进行了滑行艇在迎浪规则波中的运动响应数值预报;邹劲等[7]利用SeaKeeper对三体滑行艇进行了迎浪规则波中的运动预报;赵核毓等[8]基于CFD方法与模型试验研究了深V滑行艇的阻力和航行特性;孙华伟等[9]通过船模试验测量了三体滑行艇不同排水量、重心位置下的阻力与航态;董文才等[10]通过开展深V型滑行艇的模型纵向运动试验得到了其在规则波中的运动规律;陶磊等[11]在拖曳水池中对自主开发滑行艇的耐波性能进行了试验研究。
目前对滑行艇作为高速拖曳水面搭载平台开展的相关研究非常少,针对带尾部拖曳力的滑行艇进行阻力和运动预报还需依靠成熟的模型试验方法。拖曳状态下的航行性能是评价一个水面搭载平台的重要依据。本试验主要目的是通过模型试验方法来进行滑行艇的航行性能预报,研究滑行艇在带有尾部拖曳力情况下的阻力性能及耐波性特征,并结合试验结果和试验现象对滑行艇作为拖曳平台的特点进行分析,以验证滑行艇的高速拖曳能力。
1 模型情况及试验方法本船为长折角且深V型滑行艇,主要参数见表1。滑行艇的横剖面形状如图1所示。
|
|
表 1 船模主要参数 Tab.1 Main parameters of ship model |
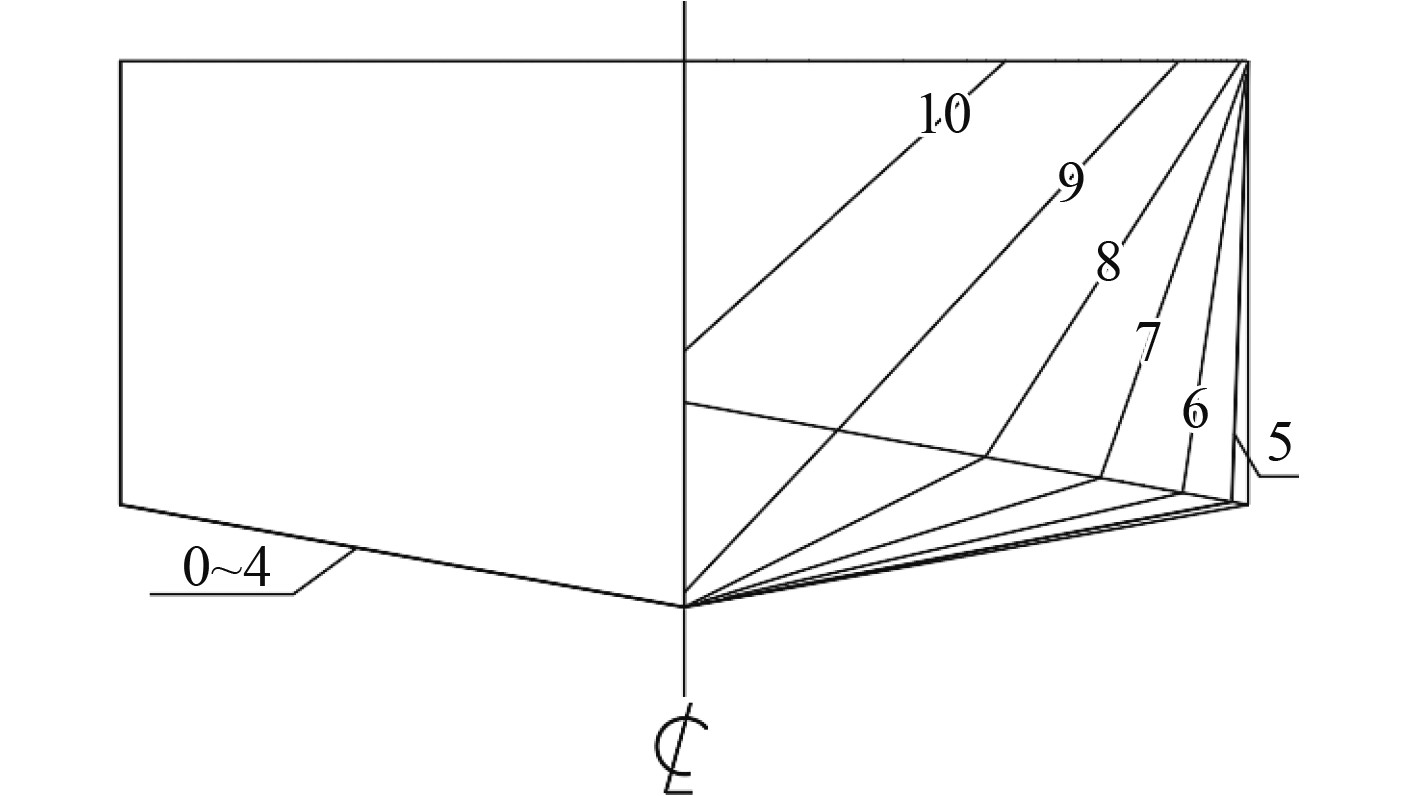
|
图 1 船模横剖线图 Fig. 1 Cross sectional plan of ship model |
本滑行艇模型为松木制作,在高速拖曳工况下为了防止纵倾角过大而出现危险,在滑行艇尾部设置有尾阻流板,尾阻流板为固定式,安装于尾封板上,向下伸出船底2 mm。另外,因本滑行艇为深V型船首,为了避免在非滑行状态下的首部飞溅过大,影响试验观察,在滑行艇首部两侧设置有压浪条,其安装起始位置从6站向船首延伸1204 mm,安装高度为距基线205 mm,宽度为15 mm。
本船尾部拖曳力幅值以线型方式进行增加,拖曳力方向与船舶航行方向相反,并沿水平向下,增加拖曳力会使滑行艇在零航速时具有不同的纵倾角和排水量。
在试验时,不同的航速对应不同的尾部拖曳力和拖曳角度,其对应关系如表2所示。其中,
|
|
表 2 不同航速下对应的拖曳力和拖曳角度 Tab.2 The corresponding towing force and towing angle at different speeds |
本船模型采用的是拖线外拖的拖曳方式,拖曳点位置在船舷两侧重心剖面的重心高度处,以尾封板龙骨最低点处为原点,拖点的坐标为(1144 mm,±412.5 mm,238 mm)。
在调节尾部拖曳力大小时,由于滑轮机构存在摩擦力,需要通过船模阻力仪测量加载对船模的水平拉力,使其实际水平拉力与理论加载水平拉力相等。根据拖点与水下滑轮之间的距离得到水下滑轮在不同角度时的入水深度,通过拖车上的手拉葫芦来控制水下滑轮的高度,即可实现尾部拖曳角度的调节。阻力仪与船模之间通过拖线连接,陀螺仪和升沉测量点均位于重心处,倾角传感器设置于船首,首部加速度传感器安装于9.5站处。
2 静水试验在静水中进行不同尾部拖曳状态的阻力试验,对比拖曳力对航行阻力的影响,同时测量预报阻力、重心处的升沉与纵倾。试验航速分为以下10个工况:1.29 m/s、2.57 m/s、3.86 m/s、5.14 m/s、5.40 m/s、5.66 m/s、6.17 m/s、6.43 m/s、7.20 m/s和7.72 m/s,对应的体积傅汝德数
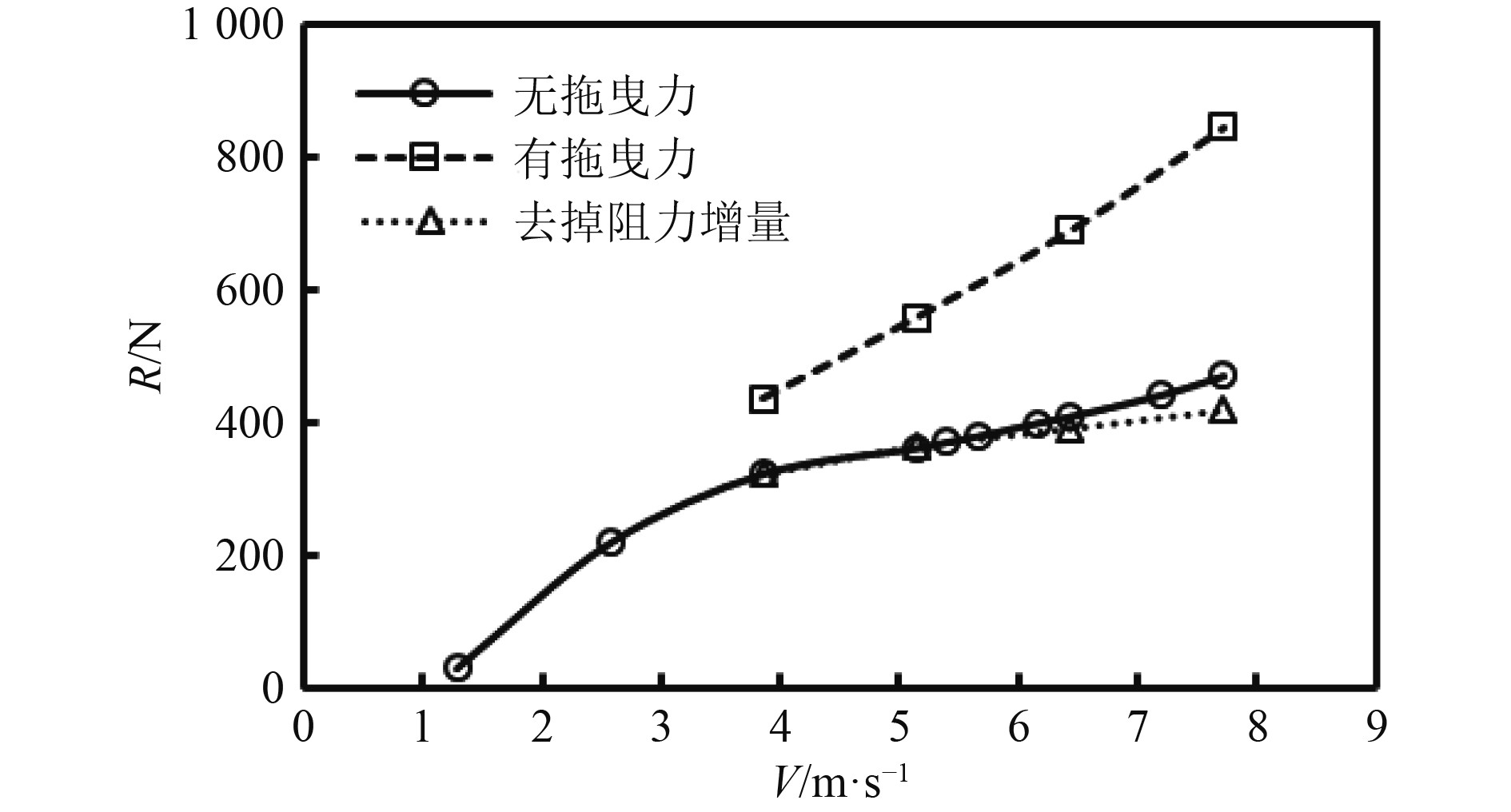
从图2的阻力曲线可看出,滑行艇在无尾部拖曳力的时候阻力性能较好,无明显的阻力峰。而增加尾部拖曳力后,随着航速的增加,阻力会大幅增加,且增幅随着航速的增加越来越大,由3.86 m/s时的34.93%增加到7.72 m/s时的79.77%。由此可见,航速的增加会使拖曳阻力越来越大,因此对于高速拖曳水面平台进行阻力预报非常必要。
|
图 2 静水中的阻力对比 Fig. 2 Comparison of resistance in clam water |
通过将拖曳阻力减除后,可发现拖曳状态的船体阻力受拖曳力的影响实际上在逐渐减小,即拖曳力引起船体浮态发生变化后使船体阻力有所降低,航速越高,纵倾越大,阻力降低的幅度也越大。在7.72 m/s时阻力降幅达10.95%,可见拖曳状态时总阻力增加的成分主要是拖曳阻力,船体阻力反而有所减小。
图3分别为船模在同航速下有无拖曳力的航态对比。可以看出,无拖曳力时船模的纵倾角在3.86 m/s之前逐渐增大,之后随着航速的提高逐渐减小。而在增加拖曳力后,低速(3.86 m/s)时纵倾增幅不太明显为9.24%,当航速增加到7.72 m/s后,由于拖曳阻力大幅增加,而拖曳阻力向下的分量会使滑行艇产生抬头力矩,从而导致此时船体纵倾增幅达到了50.93%。

|
图 3 静水中的航态对比 Fig. 3 Comparison of navigation state in clam water |
而拖曳力对船体升沉的影响就没有纵倾那么明显。在速度3.86 m/s时的升沉增量为10.39%,仅在高速阶段7.72 m/s时,艇体抬升增幅达到16.37%。
通过对船模试验中的图像进行对比,从图4可看出在高速滑行阶段

|
图 4 V= 7.72 m/s时的船模航态对比 Fig. 4 Comparison of ship model navigation state in V= 7.72 m/s |

|
图 5 V= 5.14 m/s时的船模航态对比 Fig. 5 Comparison of ship model navigation state in V= 5.14 m/s |
在耐波性试验中,进行带尾部拖曳力与不带尾部拖曳力2种状态的迎浪4个速度(
为了体现拖曳工况的影响,重力加速度取运动幅度较大的首部作为分析对象,并选择排水状态
图6为船模速度在

|
图 6 滑行艇在波浪中的阻力平均值对比 Fig. 6 Comparison of the average resistance of the planning boat in the waves |
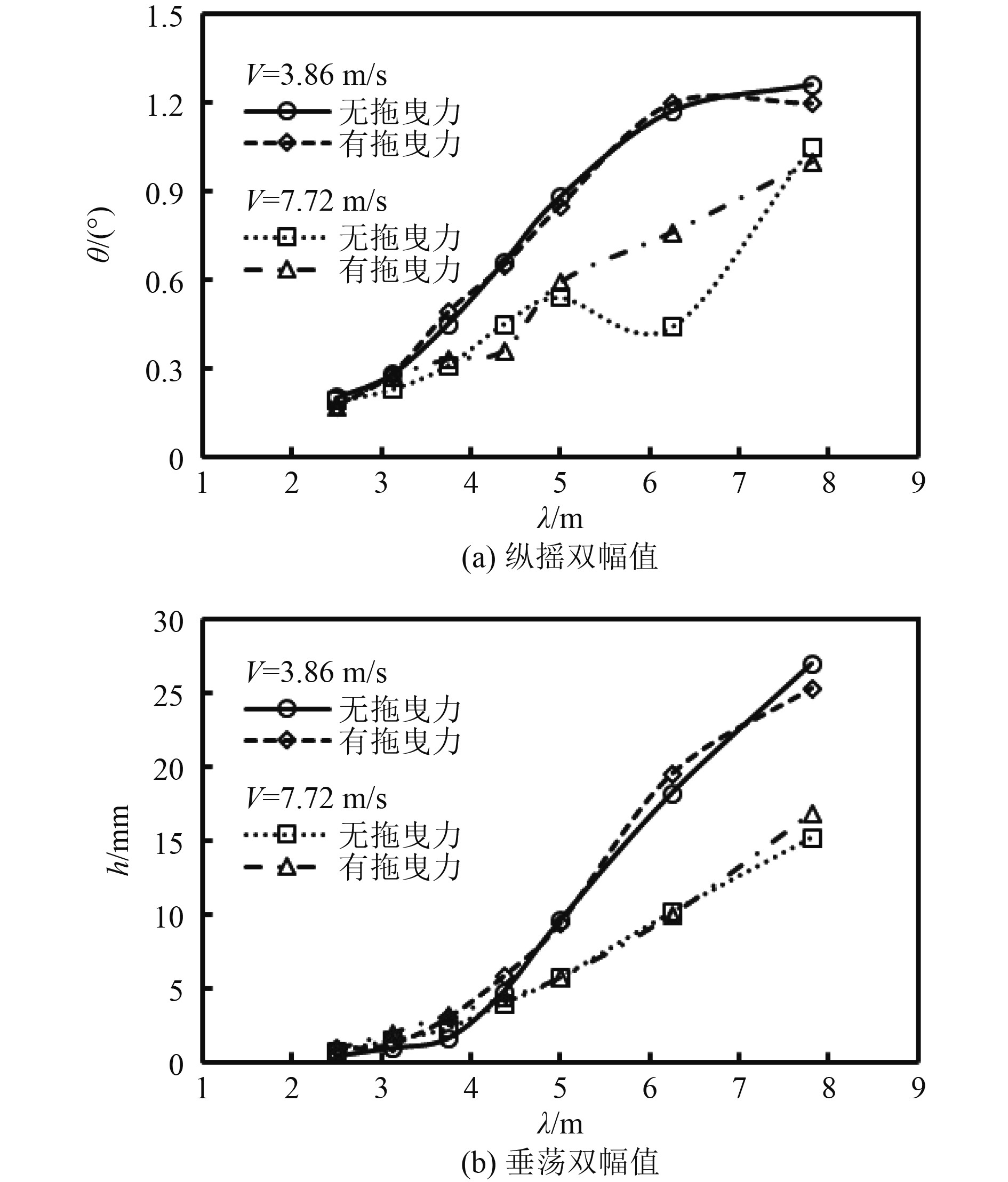
而从图7可以看出,在
|
图 7 H= 25 mm时滑行艇在波浪中的纵摇、垂荡双幅值对比 Fig. 7 Comparison of dual amplitude of pitch and heave of planning boat in waves when H=25 mm |
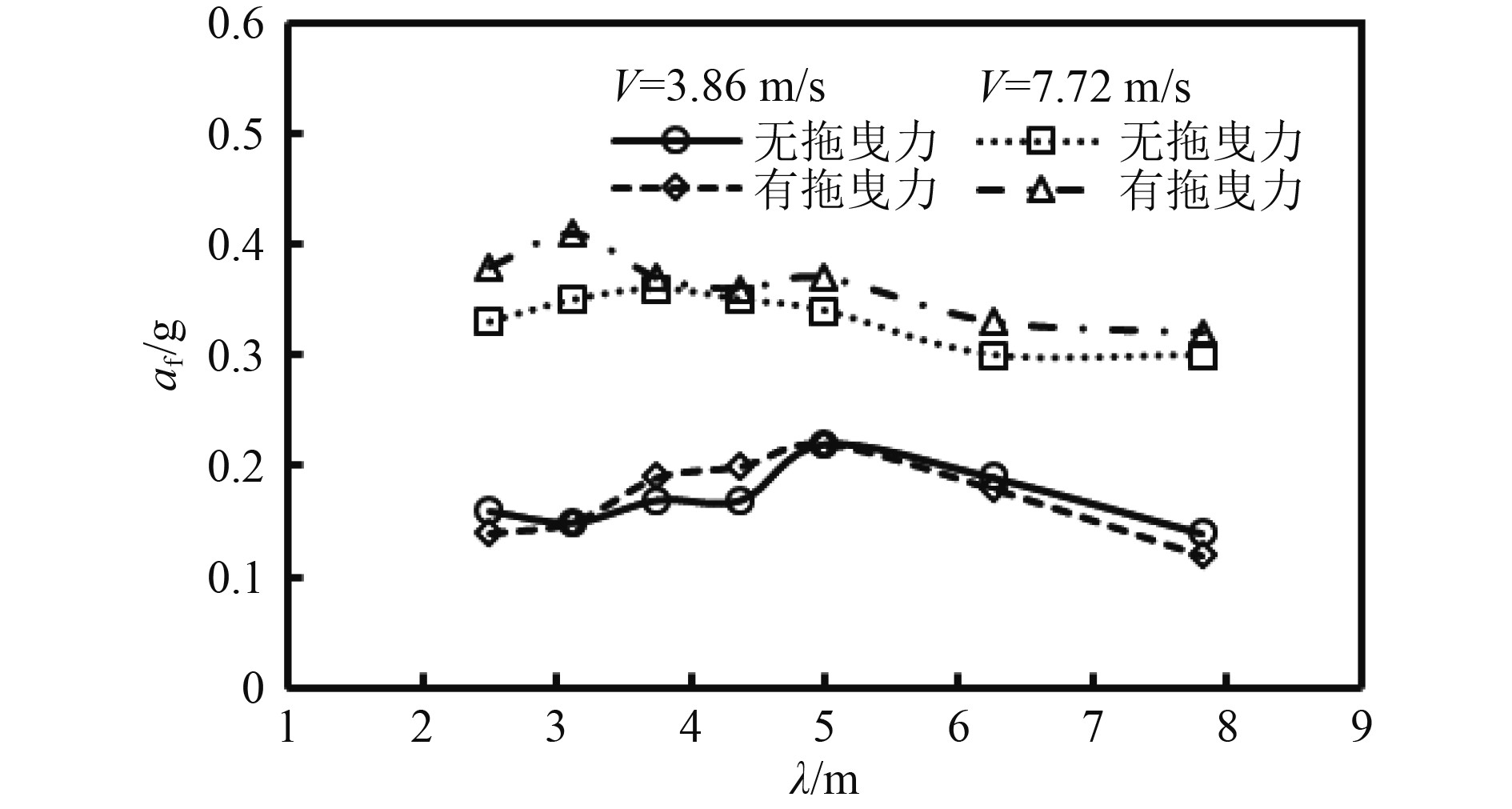
在
|
图 8 H= 25 mm时滑行艇在波浪中的首部加速度双幅值对比 Fig. 8 Comparison of double amplitude values of bow acceleration of planning boat in waves when H=25 mm |
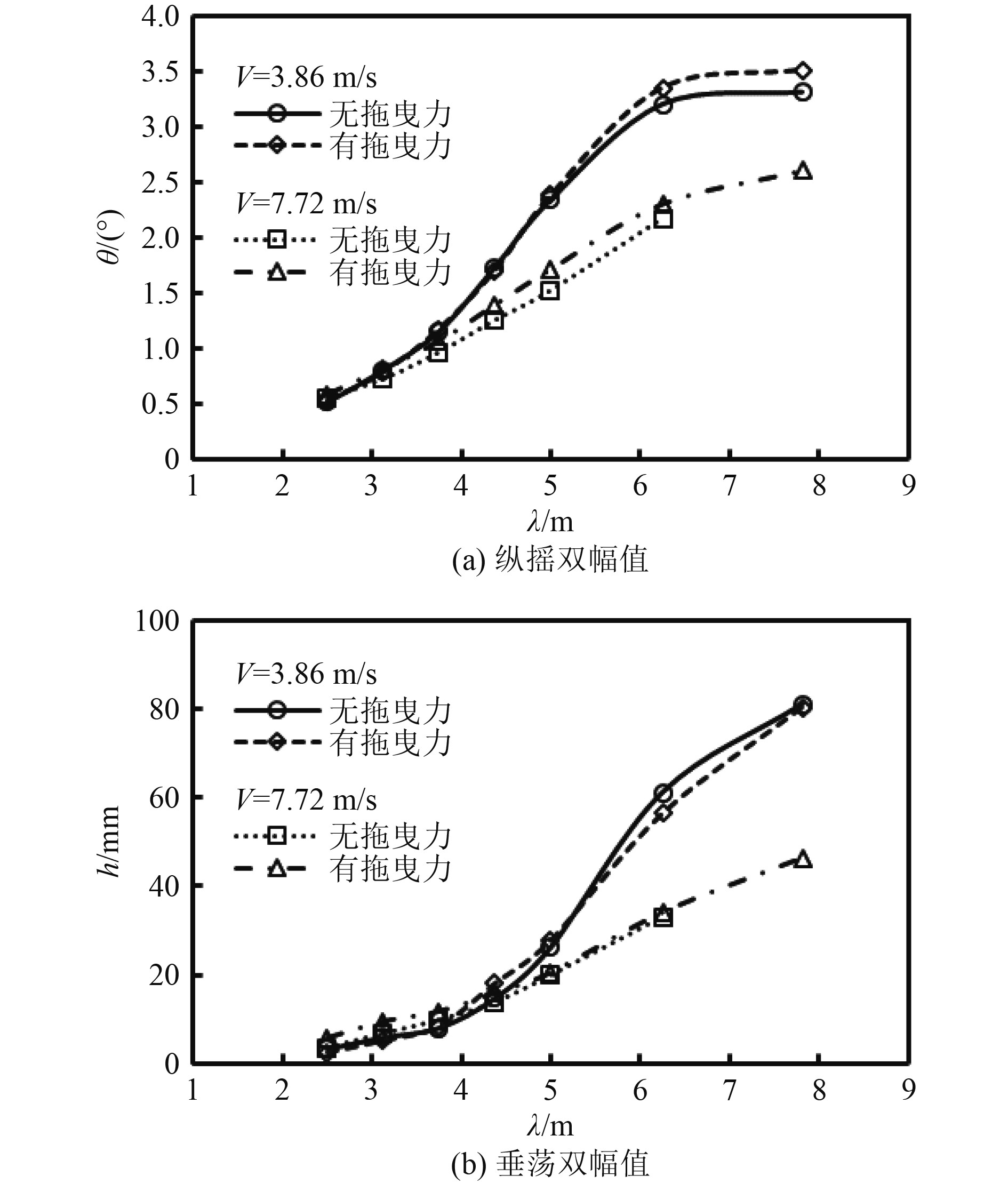
当波高增加到75 mm时,从图9可以看出,带尾部拖曳力时的垂荡与纵摇双幅值基本与不带尾部拖曳力时趋势一致。在波长较短时有拖曳力状态下垂荡双幅值会提高,如
|
图 9 H= 75 mm时滑行艇在波浪中的纵摇、垂荡双幅值对比 Fig. 9 Comparison of dual amplitude of pitch and heave of planning boat in waves when H=75 mm |
从图10可以看出,在

|
图 10 H= 75 mm时滑行艇在波浪中的首部加速度双幅值对比 Fig. 10 Comparison of double amplitude values of bow acceleration of planning boat in waves when H=75 mm |
本文首先对滑行艇进行了静水模型试验,在带有相同附体的条件下研究比较了不带尾部拖曳力和带尾部拖曳力2种情况下船体阻力及航态的变化情况。之后对规则波中不带尾部拖曳力和带尾部拖曳力2种情况下的阻力平均值、纵摇、垂荡、首部加速度双幅值进行了对比分析,研究了尾部拖曳力对滑行艇在静水及波浪中航行性能的影响。通过本文的试验研究,可得到以下结论:
1)在滑行艇尾部设置拖曳点,并将其作为高速拖曳平台可行,设置尾阻流板对抑制滑行艇过度纵倾与升沉有一定作用,有助于提高拖曳航行时的稳定性。
2)静水航行时,滑行艇尾部拖曳力对纵倾影响较大,随着航速的增加纵倾增幅越来越大,在高速滑行阶段可达50.93%。而对深沉的影响就小得多,高速滑行时的深沉增幅为16.37%。
3)在规则波中航行时,滑行艇的阻力平均值不受波高与波长的影响,在增加尾部拖曳力后的阻力增幅与静水情况下的增幅基本一致。
4)在规则波中航行时,尾部拖曳力主要影响的是滑行艇的首部加速度,特别是在
| [1] |
张莺. 高速拖曳技术研究[J]. 水雷战与舰船防护, 2011, 19(3): 37-40. ZHANG Y. Research on high speed towing technology[J]. Mine Warfare and Ship Protection, 2011, 19(3): 37-40. |
| [2] |
张莺. 高速拖曳艇设计方法研究[C]//2019年船舶结构力学学术会议论文集, 2019: 585–589.
|
| [3] |
赵连恩, 韩端锋. 高性能船舶水动力原理与设计[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007.
|
| [4] |
梁霄, 张均东, 李巍, 等. 基于FLUELT的滑行艇直航运动数值模拟计算[J]. 大连海事大学学报, 2011(1): 55-58. LIANG X, ZHANG J D, LI W, et al. Numerical simulation calculation for hydroplane direct route motion based on FLUENT[J]. Journal of Dalian Maritime University, 2011(1): 55-58. |
| [5] |
凌杰, 窦朋. 滑行艇在规则波中自航模式下的水动力特性研究[C]//2018交通运输工程大会论文集(WCTTE2018), 2018: 15−24.
|
| [6] |
凌宏杰, 王志东, 徐娇. 迎浪规则波中高速滑行艇运动响应数值预报与分析[J]. 江苏科技大学学报(自然科学版), 2019, 33(3): 1-8. LIN H J, WANG Z D, XU J. Numerical prediction and analysis of motion response of high speed planing craft in regular waves[J]. Journal of Jiangsu University of Science and Technology ( Natural Science Edition ), 2019, 33(3): 1-8. |
| [7] |
邹劲, 杨静雷, 蒋一, 等. 三体滑行艇在规则波中的数值预报[J]. 中国舰船研究, 2013, 8(3): 12-15. ZHOU J, YANG J L, JIANG Y, et al. Numerical prediction on the motion of trimaran-planing boats on regular waves[J]. Chinese Journal of Ship Research, 2013, 8(3): 12-15. |
| [8] |
赵核毓, 陈曦, 陆屿, 等. 高速深V滑行艇阻力模型试验及数值对比研究[J]. 水动力学研究与进展(A辑), 2021, 36(04): 591−598. ZHAO H S, CHEN X, LU Y, et al. Experimental and numerical study on resistance of Deep-V planing vessels[J]. Chinese Journal of Hydrodynamics, 2021, 36(04): 591−598. |
| [9] |
孙华伟, 邹劲, 黄德波, 等. 三体滑行艇阻力试验研究[J]. 哈尔滨工程大学学报, 2011, 32(7): 858–861. SUN H W, ZHOU J, HUANG D B, et al. Experimental study on a high speed trimaran-planing boat. Journal of Harbin Engineering University, 2011, 32(7): 858–861. |
| [10] |
董文才, 岳国强. 深V型滑行艇纵向运动试验研究[J]. 船舶工程, 2004(2): 14-16. DONG W C, YUE G Q. Experimental study on longitudinal motion of deep-V-shaped planing craft[J]. Ship Engineering, 2004(2): 14-16. DOI:10.3969/j.issn.1000-6982.2004.02.005 |
| [11] |
陶磊, 高霄鹏. 滑行艇波浪中运动性能试验研究[J]. 舰船科学技术, 2021, 43(3): 63-67. TAO L, GAO X P. Experimental investigation of seakeeping performance on a planning boat[J]. Ship Science and Technology, 2021, 43(3): 63-67. |
 2023, Vol. 45
2023, Vol. 45
