在国家“双碳”目标的愿景下,绿色环保的风电产业发展迅猛,同时海上风电场规模不断扩大。国内外海上风电项目逐渐呈现出远海化和深水化的特征。在满足风电场基本运维要求的基础上对船型进行优化与创新,以此来获得更好的航行性能。
M型槽道滑行艇作为近年来出现的新船型,具备速度快、适航性好的特点,在逆风、逆浪中的高速航行能力较为突出,是一款性能优异的船型[1]。为了满足运维需求,国内外装备一定数量的双体风电运维船,借鉴M型艇槽道的设计,在现有双体风电运维船的基础上,将连接桥槽道化,并对双体船槽道进行设计。
运用CFD数值仿真方法对槽道艇进行水动力的分析与计算。宴亮[2]基于STAR-CCM+探究了槽道宽度、槽道高度对M型艇水动力性能的影响,研究表明,增加这三方面的参数尺度有利于提高艇的性能。邹劲等[3]提出倒V型槽道滑行艇的设计,并对槽道滑行艇的结构进行设计和CFD水动力分析,表明在高速阶段其阻力比常规槽道滑行艇增加得缓慢。邢晓鹏等[4]研究了不同重心纵向位置、槽道高度以及底部倾斜角度对双体静水阻力的影响,分析了各个影响因素对船体静水阻力性能的作用机理。赵核毓等[5]对深V型槽道滑行艇,运用CFD软件进行静水航行数值模拟,分析了多种船型方案的阻力,研究了船体的滑行状态、不同纵心位置的阻力情况。在保证双体母型船主要要素和片体型线不变的基础上,结合双体槽道的主要特征,将连接桥部位改造成纵向变化的槽道,确定槽道参数,进一步来研究双体槽道船的阻力性能。
1 双体槽道船型及槽道参数 1.1 基本船型选取航行性能优良的双体风电运维船实船作为基本船型,双体船的主要参数如表1所示,双体船片体位置示意图如图1所示。
|
|
表 1 双体母型船的主尺度参数 Tab.1 The principle dimensions of catamaran model |
|
图 1 双体船片体位置示意图 Fig. 1 Schematic diagram of the position of the hull of the catamaran |
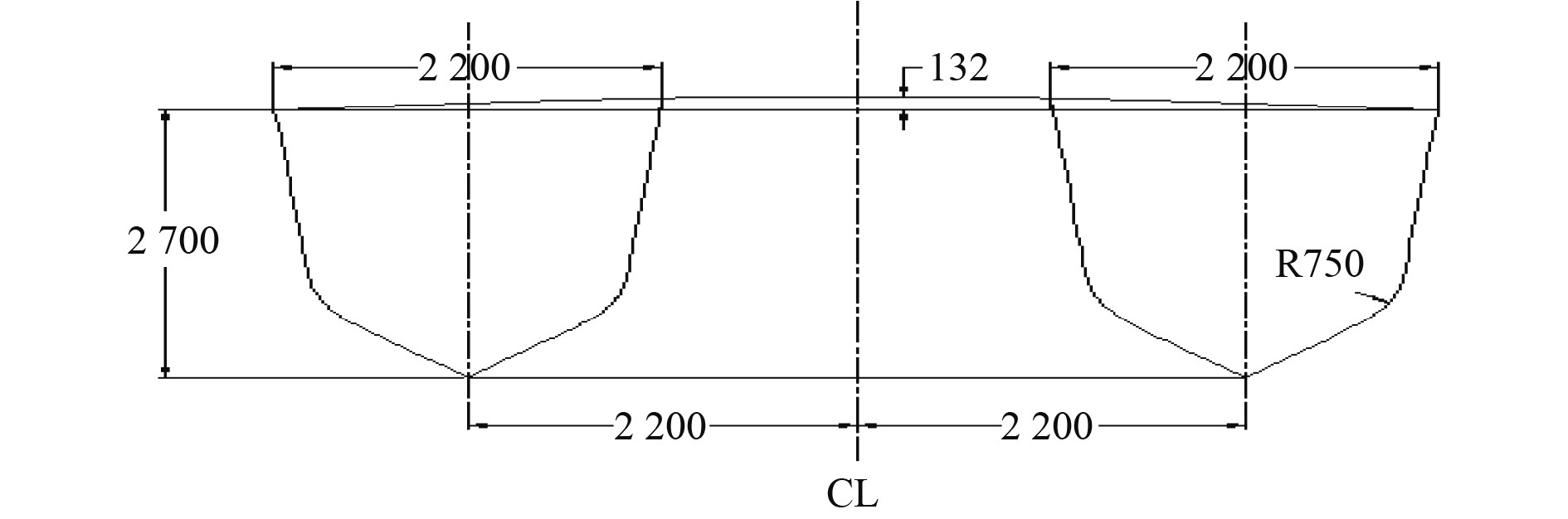
1)纵向槽道顶线
槽道顶线沿首至尾分为进流区、混合区和泄流区。3个区域的比例为
2)槽道宽度
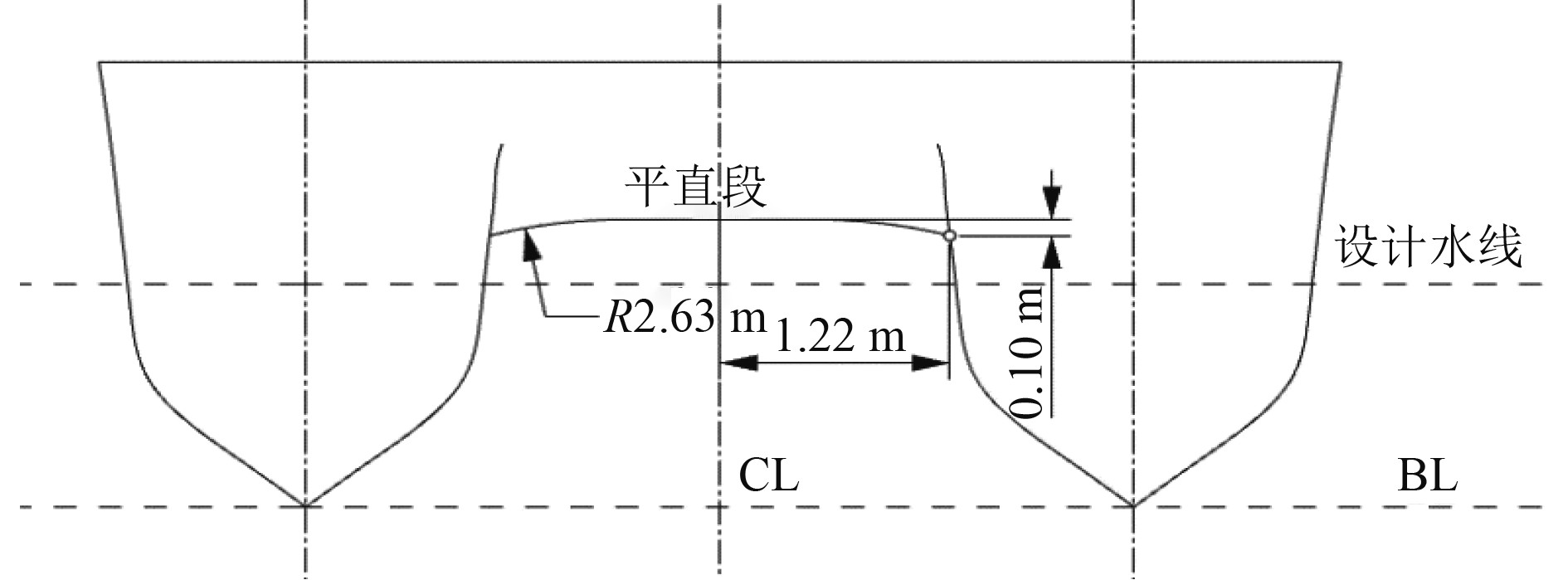
双体槽道船的横向形状为平直线型[7],即槽顶角度为0°,不仅能使气流具有更好的贯通性和流畅性,且能减小摩擦面积,进一步减小船舶阻力,故槽道顶线选择平直段连接。平直段与片体之间则以光滑圆弧的形式进行过渡,沿首至尾保持弧线半径不变,且弧线与平直段相切,并交于片体一固定点。该点距中线1.22 m,与平直段保持相对高度0.1 m。
双体船片体具有首尾瘦削且中间宽阔的特点,在设计时,并未保持首尾两端平直段宽度相等。结合槽道与弧线的特征,基本船型的首部平直段宽度为3 m,船尾平直段宽度为1.74 m。本文双体槽道船型宽为6.60 m,槽道整体宽度为4.40 m,符合槽道相对宽度b/BPS 0.35~0.69的标准。
3)槽道尾端高度
通常槽道越高,在高速航行时,其产生的阻力越小,但过高的槽道不利于滑行艇的兴波性能,而槽道过低容易发生堵塞现象,难以形成较密集的气液混合物,对滑行艇的快速性产生负向影响。基于对槽道尾部高度,即槽道顶线最低点的考虑,将槽道高度

|
图 2 纵向槽道顶线示意图 Fig. 2 Schematic diagram of top line of longitudinal channel |
|
图 3 中横剖面槽道宽度示意图 Fig. 3 Schematic diagram of channel width in cross section |
在双体母型船的基础上,结合确定好的槽道尺寸要素,运用船舶设计NAPA软件对船体进行建模。
2 系列船型方案确定 2.1 槽道顶线方案对于槽道型船,其纵向槽道参数变化会对船体阻力产生较大的影响。进流区域、混合区域对槽道型船水动力性能影响较大。为探究适合于本船的区域长度,现将泄流区长度保持不变,调整进流区和混合区长度,即混合区域最长,进流区域次之。各区域占比为
槽道各区域的长度变化会对船体阻力产生影响,同样区域交界点高度也是影响阻力的一大因素。针对该参数进行研究设计时,发现混合区和泄流区的交界点N的高度
考虑到双体槽道船是在双体船的基础上保持片体不变改造而来的,槽道高度

|
图 4 槽道高度方案 Fig. 4 Channel height scheme |
在3种不同的槽道高度方案中,每个方案对应着3种槽道顶线方案,由此可得出9个船型方案,方案参数如表2所示。
|
|
表 2 方案参数说明 Tab.2 Solution parameter description |
根据上述所确定参数,运用NAPA软件对方案1进行改造,得出不同纵向槽道方案模型。
3 阻力数值仿真 3.1 流场域和网格划分根据流场域内的特性,流场域通常设置成矩形。流场域的底部、顶部及前端均设为速度入口,后端设置成压力出口,左右两侧的流场域边界类型为对称平面,船体表面类型选择无滑移壁面。流场域的前段,位于船首向前延伸1L(L为船长)处,流场域后端设置在船尾向后延伸5L处,流场域底部由船底基线向下延伸2L。流场域顶部距离船体基线1.5L,流场域左右两侧均与船体中纵面保持2L的距离,图5为流场域示意图。

|
图 5 流场域示意图 Fig. 5 Schematic diagram of flow field |
网格划分是数值模拟中的关键环节。Marco等[8]采用重叠网格技术和变形网格技术进行了滑行艇水动力分析,认为重叠网格技术较好。采用重叠网格技术对船舶的运动状态进行求解,将重叠区域嵌套在船体模型之外,完整地包裹着船模。在创建网格时,选用表面重构、棱柱层网格生成器以及切割体网格生成器。在求解高雷诺数流动问题时发现,船体近壁面第一层网格的厚度直接影响着整体的计算精度,通常将该厚度无量纲化为
| $ {y^{\rm{ + }}}{\rm{ = }}\left( {\frac{{\Delta y}}{v}} \right) \cdot \sqrt {{\tau _\omega }{\rm{/}}\rho } 。$ | (1) |
式中:
数值仿真需模拟出复杂的瞬态多物理场问题,在运用过程中会涉及到VOF波、欧拉相、初始条件、边界条件等。主要的物理模型选择如下:隐式非定常求解器、欧拉多相流、K-Epsilon模型,同时采用默认的离散格式和松弛因子进行求解,运用典型的VOF波模型追踪自由液面,给定水面高度为船模设计吃水高度。在流场域与自由液面相交的两端激活人工阻尼进行消波,阻尼波长度一般设为2L或~1.5(
本文主要研究纵摇和垂荡对阻力的影响,故对Y轴旋转和Z轴平移2个方向进行求解。在对船模展开阻力预测分析时,时间步设为0.01 s,最大物理时间为100 s,最大内部迭代次数为10次。
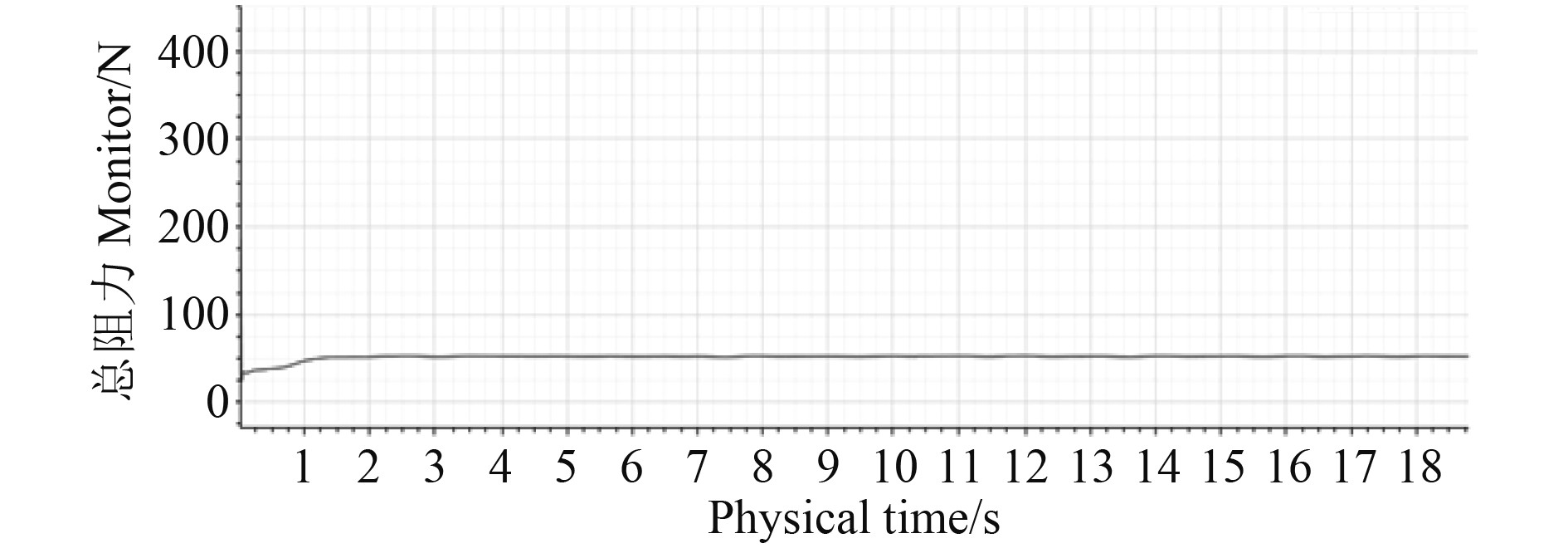
3.3 结果验证图6为双体船在时阻力仿真值,船模的静水阻力仿真值为51.53 N。通过Froude换算法可得出相应实船阻力的仿真值为46.26 kN,与其双体实船的试验值45.15 kN[10]较为接近,误差为2.45%,这说明运用STAR-CCM+软件适用于双体船的静水阻力研究。
|
图 6 双体船在V=2.45 m/s时阻力仿真值 Fig. 6 Simulation value of catamaran resistance at V=2.45 m/s |
基于1∶10的缩放比例,将改造的9个双体槽道船方案以及双体船,在船模航速分别为3.5 m/s(Fr=0.787)、4 m/s(Fr=0.899)、4.5 m/s(Fr=1.012)、5 m/s(Fr=1.124)、5.5 m/s(Fr=1.237)时进行了静水阻力计算,图7为不同速度下的静水阻力值。

|
图 7 双体槽道船型方案与双体母型船阻力对比 Fig. 7 Comparison of resistance between catamaran channel ship type and catamaran mother ship |
对比图中各方案的静水阻力可发现,总体的变化规律趋于一致。双体母型船船模在速度不断提升后其船身受到的阻力急剧增加,而双体槽道运维船的阻力增长较为缓和。当V>4 m/s时,9个双体槽道风电运维船方案的阻力性能远远优于双体船,以服务航速V=4.5 m/s为例,各方案的阻力改善比均在11%以上。
1)槽道高度变化对静水阻力的影响
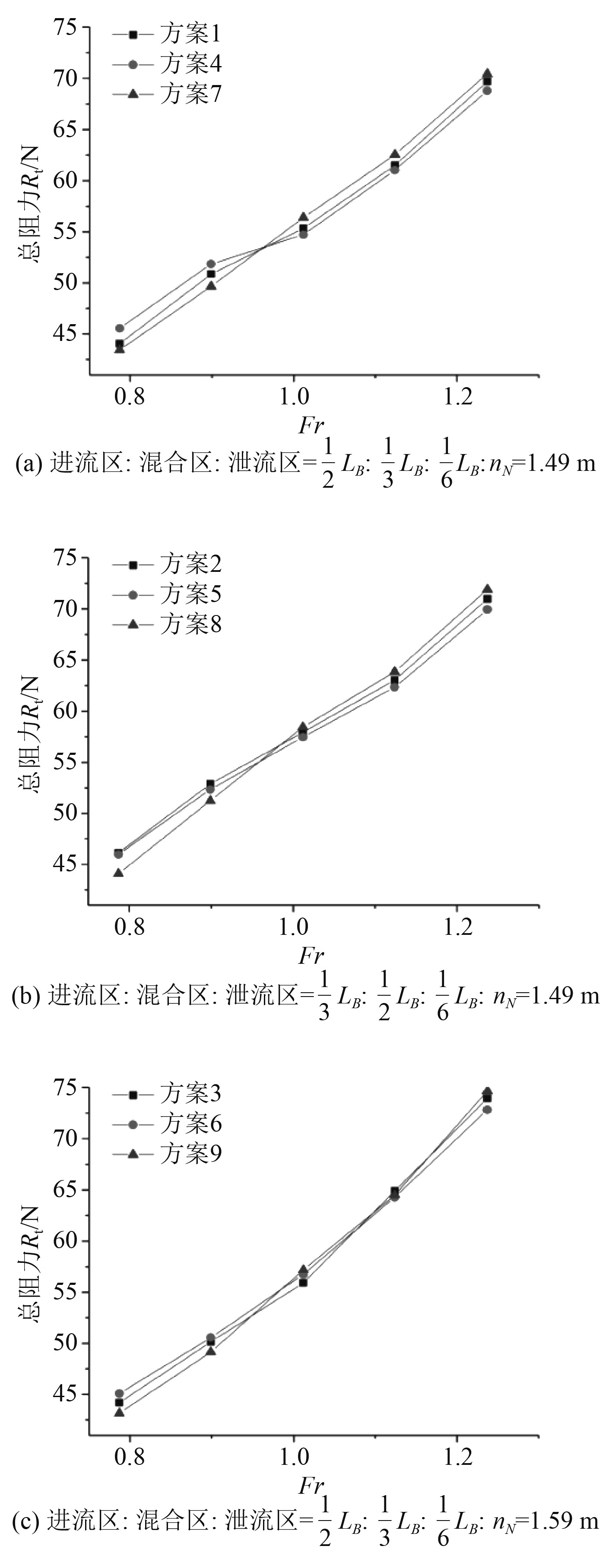
图8为不同槽道高度下阻力对比曲线图。整体而言,各方案阻力上升的趋势较为一致。当
|
图 8 不同槽道高度阻力值 Fig. 8 Resistance values of different channel heights |
由图8(a)可知,槽道高度较低的方案4更具有优势,比方案1与方案7的阻力值要小。由此可知,在同一槽道顶线参数下,随着航速的提高,槽道空间较大,气液混合物被挤压的程度较小,无法提供较大的气动升力从而影响航行姿态,致使阻力性能变差。因此,在确定该参数时,槽道高度略低于设计水线,更有利于运维船高速航行时的阻力性能。
2)槽道顶线参数变化对静水阻力的影响
图9为不同槽道顶线参数之间的阻力对比,当傅式数
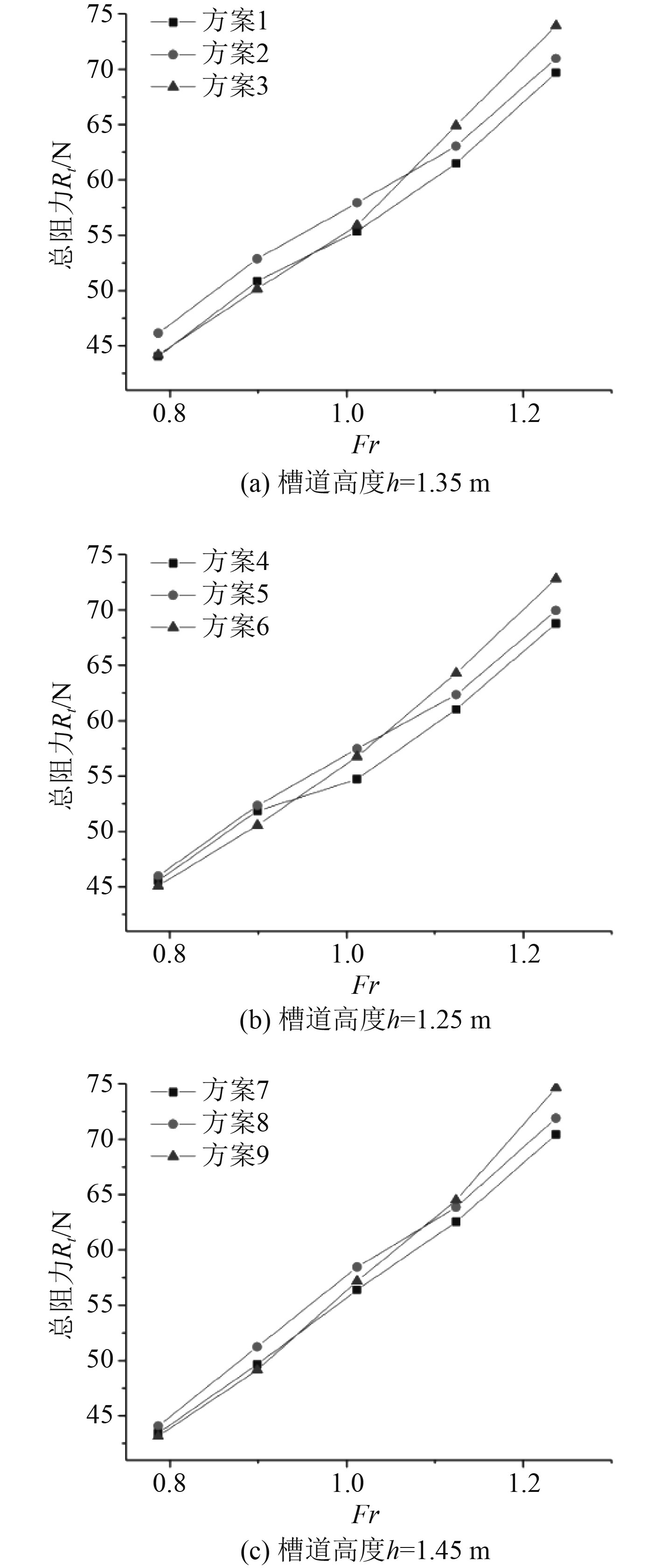
|
图 9 不同槽道顶线参数阻力值 Fig. 9 Resistance values of parameter of different longitudinal channels |
①工作区域长度变化对静水阻力的影响
以图9(a)中方案1和方案2为例,在各航速下,方案1(进流区长度较长)的阻力平均比方案2(混合区长度较长)小2.852%。可知,对于双体槽道船型来说,进流区的长度偏长具有更好的阻力性能。
②混合区与泄流区交界点高度
以方案1和方案3为例,当槽道高度以及槽道工作段长度保持一致时,方案1要优于方案3。由此可知,当船舶处于中高航速阶段时,槽道内部进气量急剧增大。若交界点高度较大,则大量汇聚的气液混合物阻塞槽道,导致其阻力迅速增大。
5 结 语1)与双体母型船相比,船舶的航速越高,双体槽道风电运维船所受到的阻力优势越明显。
2)针对双体槽道船而言,对比槽道尾端高度位置可发现,船舶以较高的航速前进时,当升高槽道高度,阻力呈上升趋势;当槽道高度略低于设计水线时,具有更好的阻力性能。
3)在静水阻力仿真中,双体槽道运维船的纵向槽道参数变化对船体阻力影响明显,较长的进流区阻力更有优势。
| [1] |
黄武刚. M型艇与槽道型艇的阻力和耐波性比较[J]. 船海工程, 2015, 44(1): 56-59. DOI:10.3963/j.issn.1671-7953.2015.01.014 |
| [2] |
晏亮. 滑行槽道对M型艇静水消波性能影响及耐波性研究[D]. 武汉: 武汉理工大学, 2020.
|
| [3] |
邹劲, 韩晓坤, 张元刚. 倒V型槽道滑行艇船型的水动力性能研究[J]. 船舶, 2017, 28(6): 13-20. DOI:10.19423/j.cnki.31-1561/u.2017.06.013 |
| [4] |
邢晓鹏, 邵文勃, 马山. 基于CFD的槽道滑行艇阻力性能研究[C]//第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议论文集, 2002: 1371–1376.
|
| [5] |
赵核毓, 陈曦, 陆屿. 高速深V滑行艇阻力模型试验及数值对比研究[J]. 水动力学研究与进展, 2021(7): 1-2. |
| [6] |
孙聪, 张亮, 冯峰, 等. 基于CFD的M型槽道滑行艇消波特性分析[C]//2017年中国造船工程学会优秀学术论文集, 哈尔滨, 中国造船工程学会, 2018: 143−156.
|
| [7] |
FRISK D, TEGEHALL L. Prediction of high-speed planing hull resistance and running attitude[D]. Chalmers: Chalmers University of Technology, 2015.
|
| [8] |
MARCO A D, MANCINI S, MIRANDA S, et al. Experimental and numerical hydrodynamic analysis of a stepped planning hull[J]. Applied Ocean Research, 2017, 64: 135−154.
|
| [9] |
谢云平, 赵子健, 谢蔚刚. 三体槽道船船型设计及阻力性能研究[J]. 船舶工程, 2020, 42(3): 43-46+62. DOI:10.13788/j.cnki.cbgc.2020.03.08 |
| [10] |
马晶晶. 双折角滑行艇阻力及运动性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
 2023, Vol. 45
2023, Vol. 45
