NURBS曲线是一种用于表示和建模曲线和曲面的数学工具,它具有较高的灵活性和精确性,可以通过控制点和权重来调整曲线的形状。在船体曲面结构设计中,可以利用NURBS曲线来建模船体的外形和内部结构,通过调整控制点和权重来优化曲面的形状,以满足设计要求。小波变换是一种数学工具,用于分析信号的时频特性。在船体曲面结构设计中,可以利用小波变换来分析船体曲面的局部特性,如曲率、法向量等。通过对曲面进行小波变换,可以获取曲面的局部特性信息,并根据设计要求进行优化调整。
本文的研究方向是基于NURBS和小波变换的船体曲面结构优化设计方法,重点介绍了基于NURBS进行船体曲线和曲面的拟合过程,逐步优化船体曲面结构设计,以达到最优的设计效果。
1 NURBS样条曲线的基本研究非均匀有理B样条(NURBS样条)曲线具有局部性、灵活性、自由曲面表达清晰等优点,在二维三维CAD产品设计中有广泛的应用,其表达式为:
| $ p(u) = \frac{{\displaystyle\sum\limits_{i = 0}^n {{N_{i,k}}} (u){d_i}{\omega _i}}}{{\displaystyle\sum\limits_{i = 0}^n {{N_{i,k}}} (u){\omega _i}}} \text{。} $ |
式中:
B样条曲线的节点矢量为
| $ \left\{ {\begin{array}{*{20}{l}} {{{N}_{i,0}}({t}) = \left\{ {\begin{array}{*{20}{l}} {1,{{t}_i} \leqslant t < {t_{i + 1}}} ,\\ {0,{\rm{else}}} ,\end{array}} \right.} \\ {{N_{i,p}}({t}) = \frac{{{t} - {{t}_i}}}{{{{t}_{i + p}} - {{t}_i}}}{{N}_{i,p - 1}}({\rm t}) + \frac{{{{t}_{i + p + 1}}}}{{{{t}_{{\text{i}} + 1}}}}{{N}_{i + 1,p - 1}}(t)} ,{\rm else}。\\ \end{array}} \right. $ |
式中:
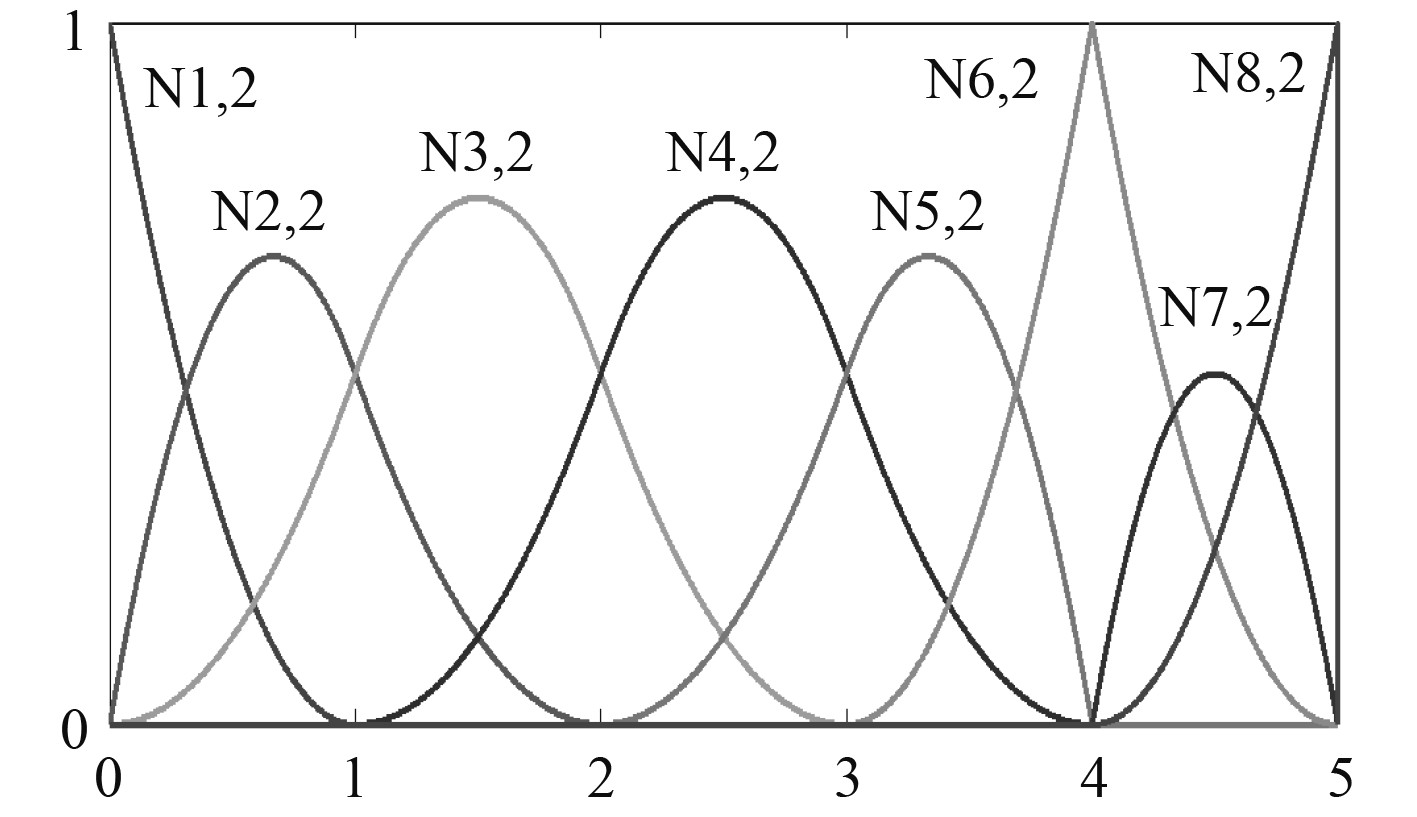
NURBS样条的基函数是一组用于定义NURBS曲线和曲面的数学函数,常用的基函数为幂函数[1]、多项式函数等,如图1所示。
|
图 1 NURBS样条的基函数曲线示意图 Fig. 1 Schematic diagram of the basis function curve of NURBS splines |
NURBS样条具有以下特性:
1)局域非负性
| $ {N_{t,p}}(t)\left\{ {\begin{array}{*{20}{l}} { \geqslant 0},\; {t \in \left[ {{t_i},{t_{i + p + 1}}} \right]},\\ { = 0,\;\rm{else}}。{{\text{ }}} \end{array}} \right. $ |
2)递推性
| $ {{{N}}_{i,p}}({{t}}) = F\left( {{{{N}}_{{{i}},p - 1}}({{t}})} \right) \text{。} $ |
3)归一性
| $ \sum\limits_{i = 0}^n {{N_{i,p}}} (t) = 1 \text{。} $ |
4)正数性。
| $ {N_{t,p}}(t) \geqslant 0 \text{。} $ |
NURBS样条曲线具有局部控制性,即修改一个控制点只会影响与之相邻的部分曲线或曲面,同时具有良好的插值性,即可以通过控制点完全重建曲线或曲面。
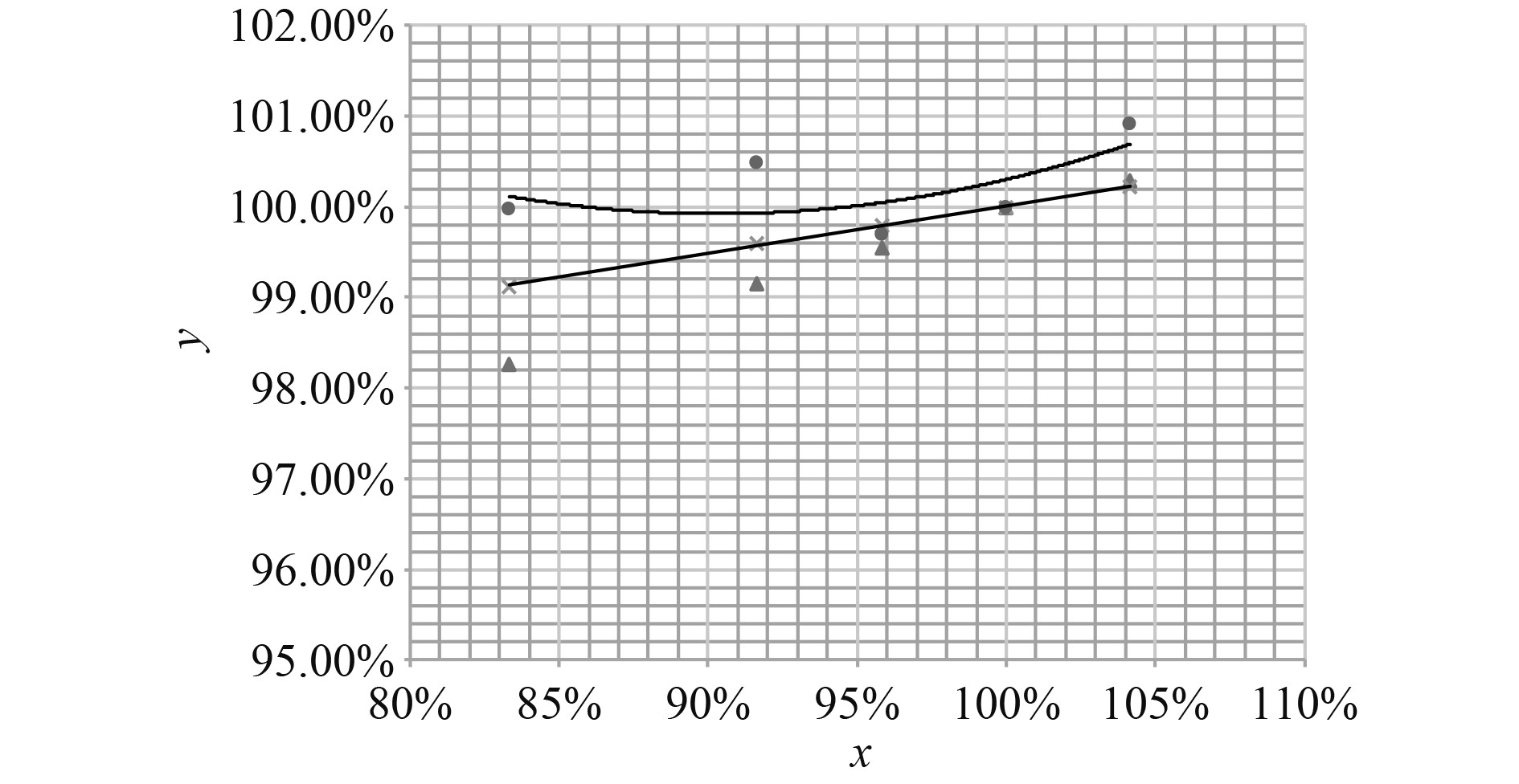
图2为基于NURBS样条曲线的插值拟合实例。可知,基于NURBS样条可得到5个节点产生的拟合曲线,拟合效果较好。
|
图 2 基于NURBS样条曲线的插值拟合实例 Fig. 2 Example of interpolation fitting based on NURBS spline curves |
多分辨小波变换(Multiresolution Wavelet Transform)是一种信号处理技术,用于将信号分解成不同频率的子信号,它基于小波函数,通过多次迭代将信号分解成低频和高频分量,从而实现对信号的多尺度分析。
多分辨小波变换的理论基础是小波分析和多尺度分析。小波分析是一种数学工具,用于将信号分解成一组基函数(小波函数)的线性组合。这些基函数具有不同的频率和尺度,可以用于描述信号在不同频率和时间尺度上的变化。多尺度分析是一种信号处理方法,用于将信号分解成不同尺度的子信号,以便更好地理解和处理信号的特征。
多分辨小波变换的优点是可以对信号进行多尺度分析,同时保留信号的时域和频域信息。它在信号压缩、图像处理、语音识别等领域具有广泛的应用。
对于某非线性信号
| $ \int\limits_R^{} {} {\left| {\frac{{x\left( \omega \right)}}{\omega }} \right|^2}{\rm{d}} \omega \leqslant \infty \text{。} $ |
式中:
| $ {x_s}\left( t \right) = \frac{1}{{\sqrt s }}x\left( {\frac{{t - \alpha }}{s}} \right) \text{。} $ |
式中,s和
信号的傅里叶变换为
| $ \begin{gathered} W{T_f}\left( {s,t} \right) = \left\{ {f\left( t \right),x\left( t \right)} \right\} = \frac{1}{{\sqrt s }}\int\limits_{}^{} {f\left( t \right)} x\left( {\frac{{t - \alpha }}{s}} \right){\rm{d}}t \text{。} \end{gathered} $ |
多分辨小波变换的步骤如下:
步骤1 选择合适的小波函数作为基函数,常用的小波函数有Haar小波、Daubechies小波[2]、Morlet小波函数等。Haar小波函数在信号压缩等领域有着广泛的应用,其表达式如下:
| $ \psi \left( t \right) = \left\{ \begin{split} &1,\;\;0 < t < \frac{1}{2} ,\\ &- 1,\frac{1}{2} < t < 1 ,\\ &0,\;\;{\rm{else}。} \\ \end{split} \right. $ |
Morlet小波函数是一个复指数函数,其实部表示信号的振幅变化,虚部表示信号的相位变化,其模型为:
| $ M\left( t \right) = C{e^{\frac{{{t^2}}}{2}}}\cos \left( {5t} \right) \text{。} $ |
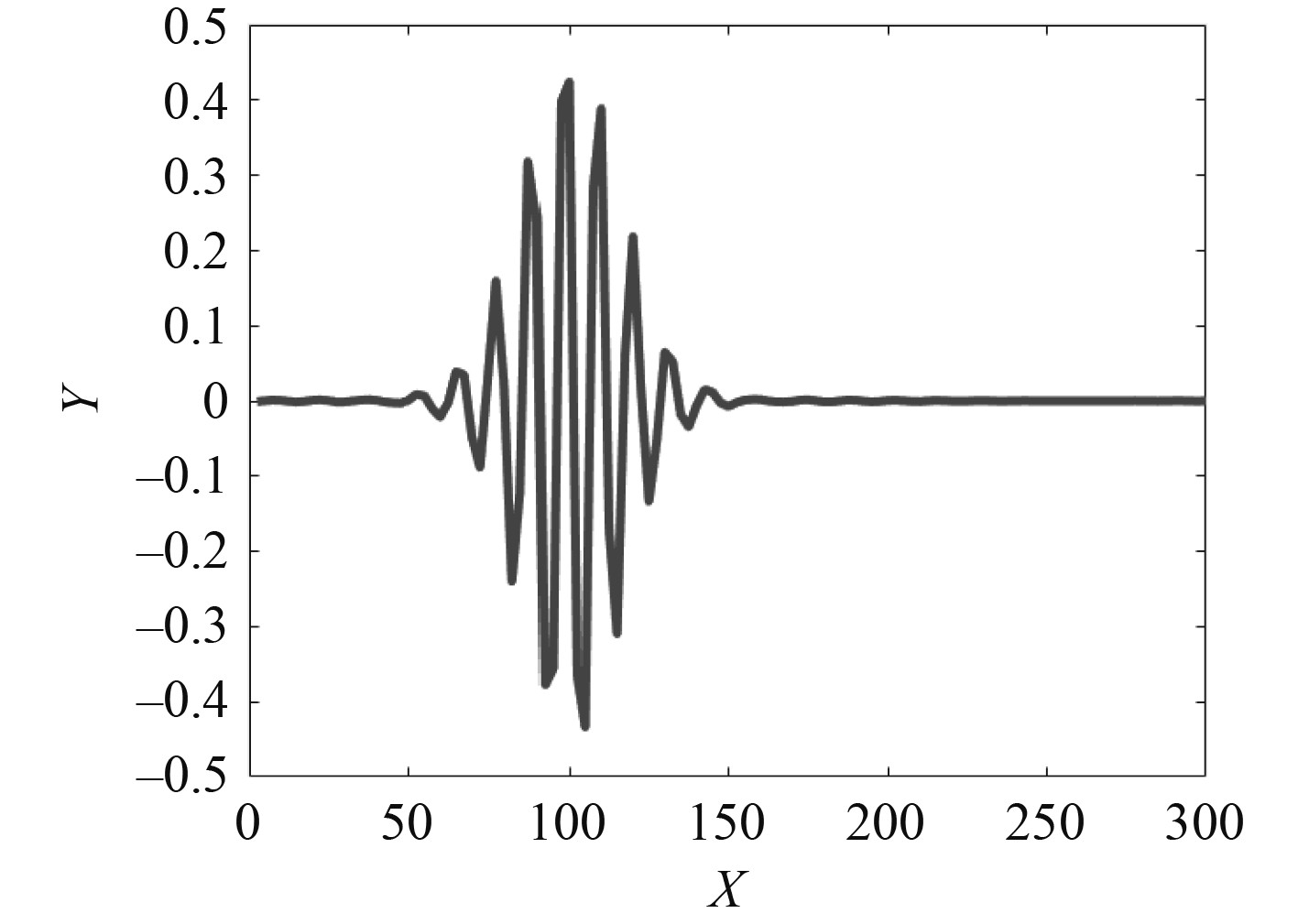
图3为Morlet小波函数的波形图。
|
图 3 Morlet小波函数波形图 Fig. 3 Morlet wavelet function waveform |
步骤2 对信号进行多次迭代分解,将信号分解成低频和高频分量。低频分量表示信号的整体趋势和低频成分,高频分量表示信号的细节和高频成分。
步骤3 重复步骤1和步骤2,直到达到所需的分辨率或分解层数。
3 基于NURBS和小波变换的船体结构拟合 3.1 基于NURBS样条曲线的船体曲线优化设计利用非均匀B样条函数进行了船体的型线设计,具体步骤如下:
步骤1 结合数据库的曲线型值数据,采用插值法生成初始的B样条曲线。型线的顶点为:
| $ {V_{i,j}}\left( {i = 0,1,...,m;j = 0,1,...,n} \right) \text{。} $ |
参数方向矢量分别如下:
| $ F = \{ \underbrace {0,{t_{p + 1}}, \cdots ,{t_n},1}_{p + 1}\} ;K = \{ \underbrace {0,{w_{q + 1}}, \cdots ,{w_n},1}_{q + 1}\} \text{。} $ |
生成非均匀B样条曲线为:
| $ S(F,K) = \sum\limits_{i = 0}^n {\sum\limits_{j = 0}^n {{N_{t,p}}(F)} } {N_{j,p}}(K){V_{i,j}} 。$ |
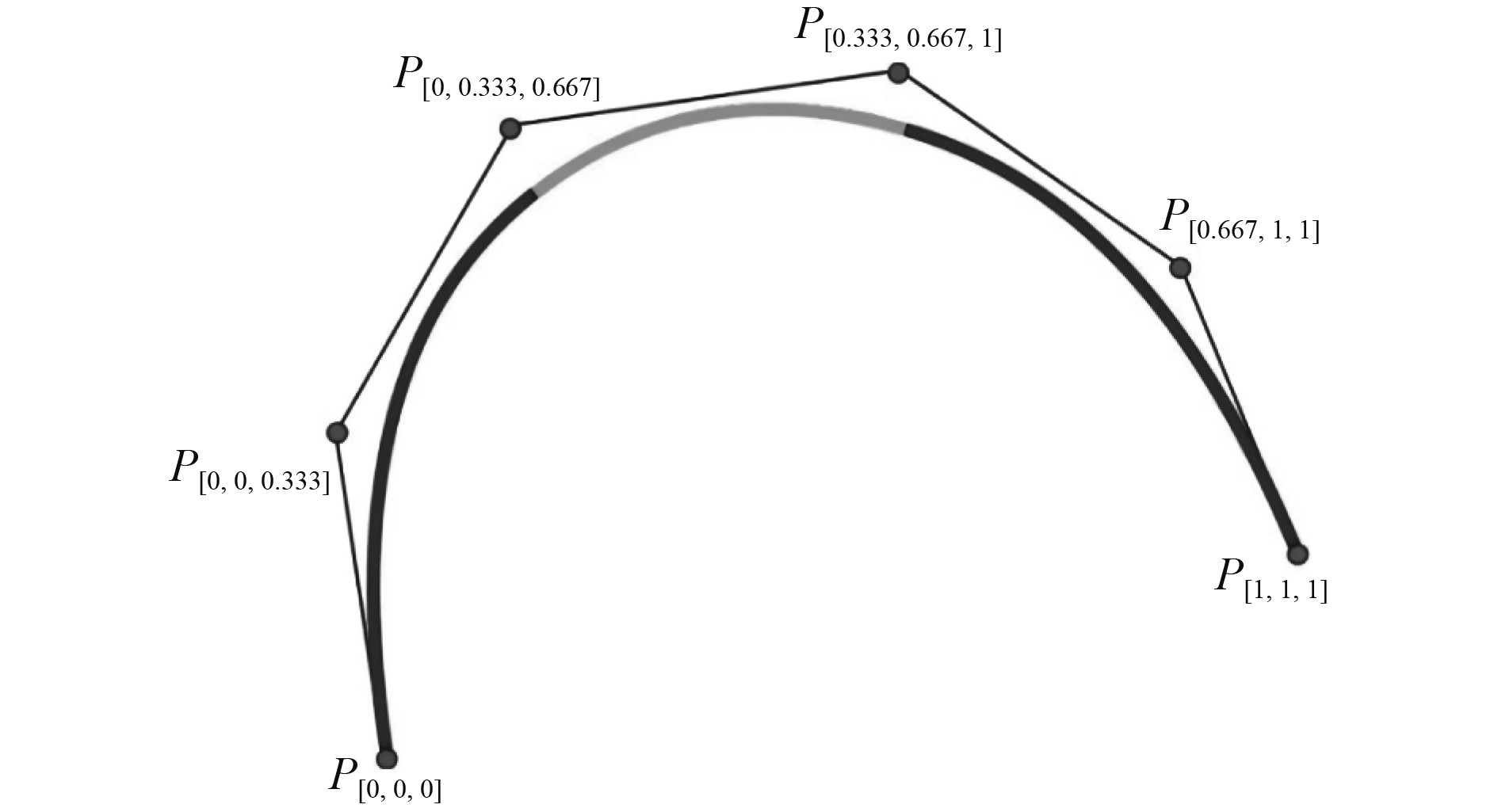
|
图 4 B样条的P次节点曲线控制示意图 Fig. 4 Schematic diagram of P-degree node curve control for B-spline |
步骤2 基于多分辨小波变换算法,对型线方程进行多尺度分析,通过插值生成B样条曲线的控制节点。
步骤3 对于船体某些复杂边线,如纵剖线等,如果边线的最低点没有数据,则重复步骤2中的插值,产生复杂边线的最低点,然后进行曲线的拟合。
步骤4 依次利用B样条曲线的节点,拟合产生船舶的水线、纵剖线、龙骨线等型线。
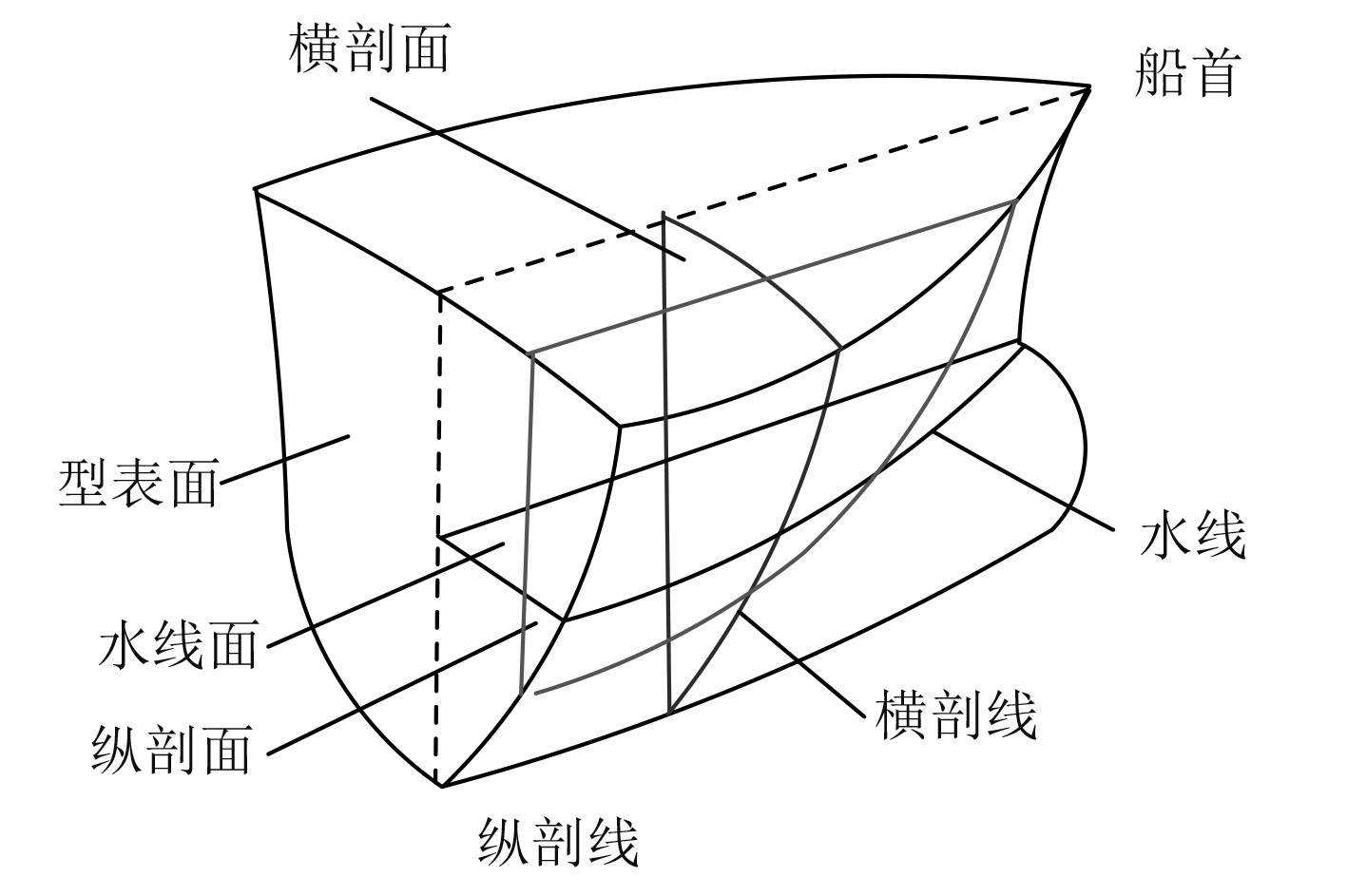
图5为基于B样条生成的船舶型线、型面示意图。
|
图 5 基于B样条生成的船舶型线、型面示意图 Fig. 5 Schematic diagram of ship lines and surfaces generated based on B-splines |
其中,型线包括纵剖线、横剖线、水线等,型面包括水线面、型表面、纵剖面、横剖面等。
3.2 基于NURBS样条曲线的船体曲面设计船舶曲面拟合是在曲线拟合的基础上完成的,包括以下关键环节:
1)曲面连续性判断
基于NURBS的曲面表达式为:
| $ S(u,v) = \frac{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{\omega _{i,j}}} } {d_{i,j}}{N_{i,k}}(u){N_{j,l}}(v)}}{{\displaystyle\sum\limits_{i = 0}^n {\displaystyle\sum\limits_{j = 0}^m {{\omega _{i,j}}} } {N_{i,k}}(u){N_{j,l}}(v)}} \text{。} $ |
假定2个相邻曲面
| $ {\left. {\frac{{\partial {S^2}(u,v)}}{{\partial u}}} \right|_{u = 0}} = {\left. {p(v)\frac{{\partial {S^1}(u,v)}}{{\partial u}}} \right|_{u = 1}} + {\left. {q(v)\frac{{\partial {S^1}(u,v)}}{{\partial v}}} \right|_{u = 1}} \text{。} $ |
此时2个曲面称为二阶连续。
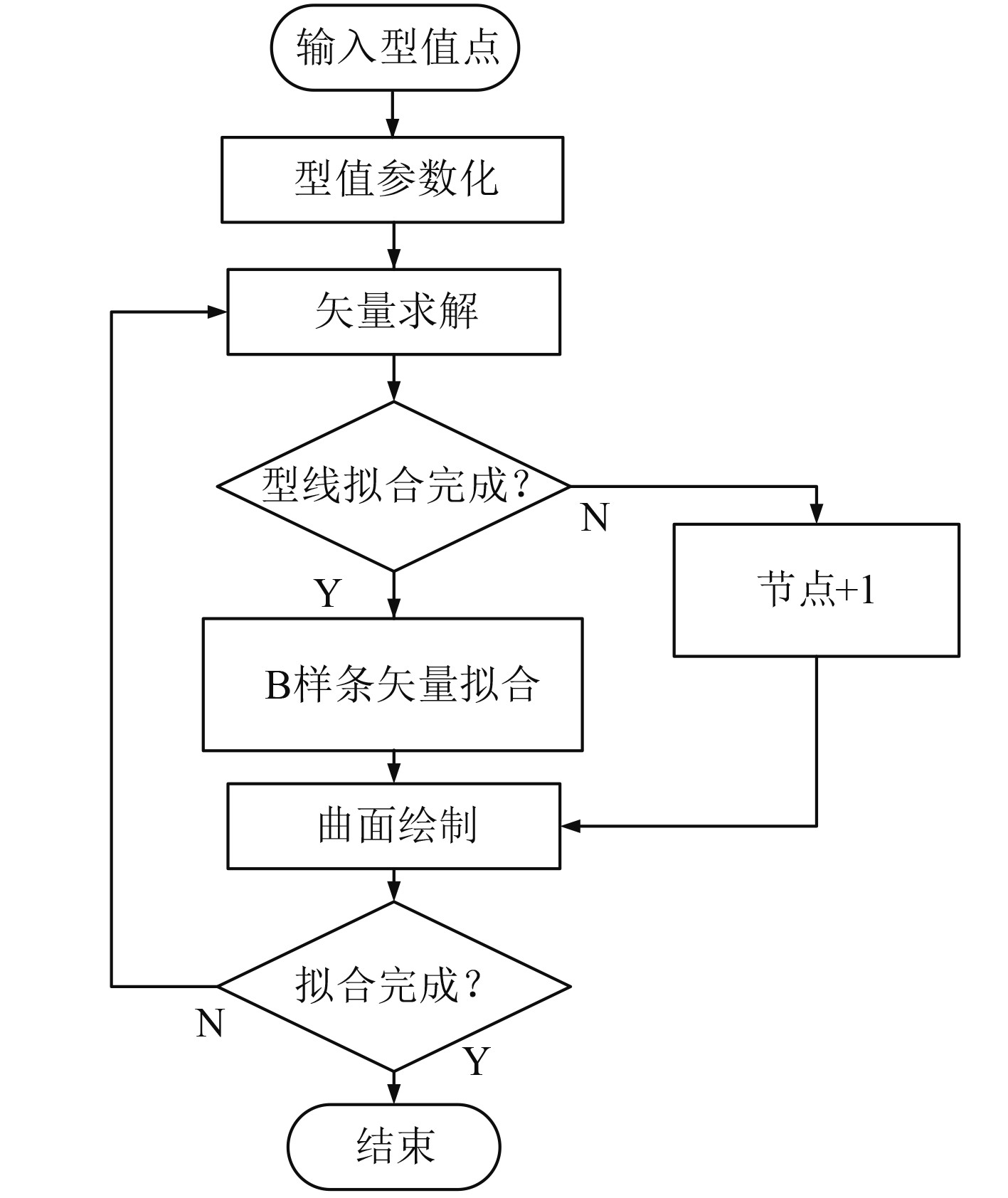
基于NURBS的船舶曲面拟合流程如图6所示。
|
图 6 基于NURBS的船舶曲面拟合流程图 Fig. 6 NURBS based ship surface fitting process |
2)曲面的连接
由于船体造型复杂,难以用单个曲面拟合整体的复杂曲面,因此,需要将曲面划分成若干个曲面片,然后通过光滑的连接形成最终的曲面。
本文使用OpenGL进行船体曲面的连接,OpenGL是由SGI公司开发的一种三维图像库开发平台,OpenGL进行船体曲面拟合的基本步骤为:
步骤1 创建一个OpenGL程序并设置窗口大小。
步骤2 创建一个缓冲对象(Vertex Buffer Object,VBO)来存储输入的曲面数据。然后创建一个几何着色器(Geometry Shader),并将其附加到OpenGL程序中。在几何着色器中,编写代码来对输入的曲面进行细分,将细分后的曲面数据写入缓冲对象(Output Vertex Buffer Object,OVBO)。
步骤3 在几何着色器中,设置输出的图元类型为三角形带(Triangle Strip),使用gl_Position变量来设置输出顶点的位置,使用gl_PrimitiveID变量来设置输出顶点的索引,使用gl_in变量来访问输入的顶点数据。
步骤4 基于B样条进行曲面拟合,建立顶点之间的连接曲面,最终使用gl_out变量来输出曲面[4]。
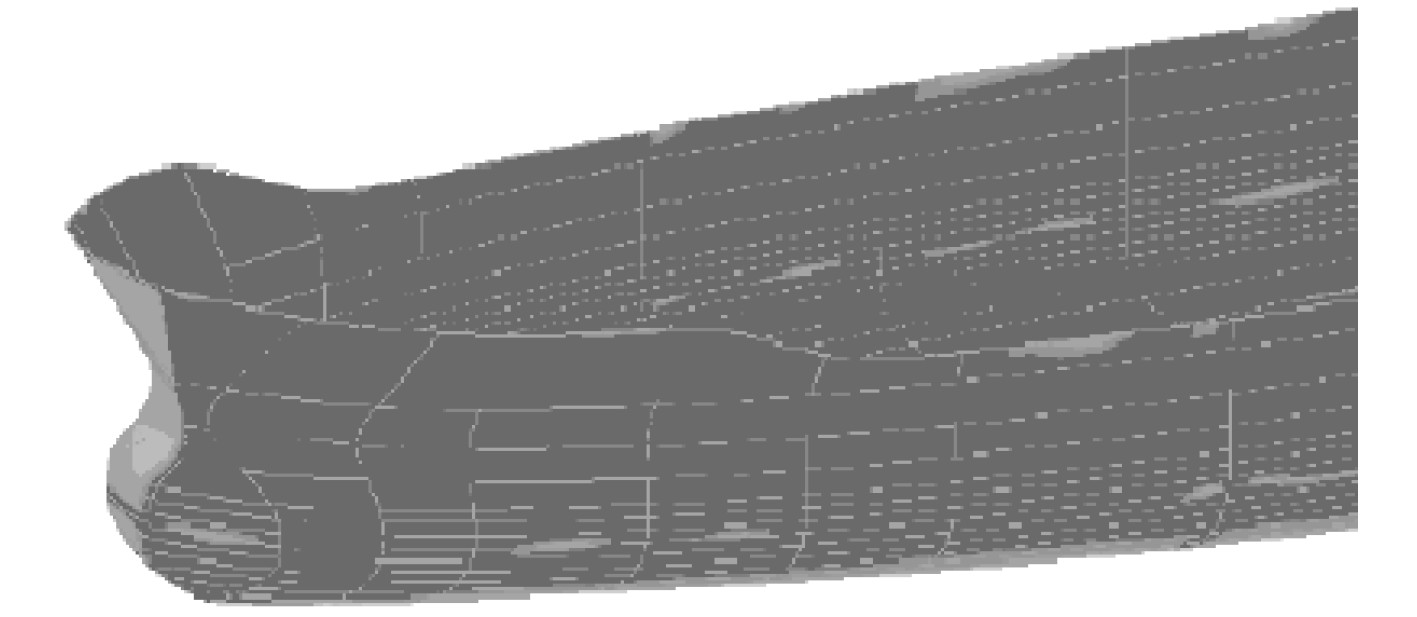
图7为基于OpenGL平台的船体曲面拟合效果图。
|
图 7 基于OpenGL平台的船体曲面拟合效果图 Fig. 7 Fitting diagram of ship hull line and curved surface |
图中可见,基于OpenGL平台的船体曲面拟合为多个曲面,不同曲面之间采用光滑连接。
4 结 语为了提高船体型线和曲面结构的设计水平,本文研究一种基于NURBS和小波变换的船体曲面结构优化设计方法。该方法一方面利用了NURBS曲线在特征型线的拟合优势,另一方面利用了多分辨小波变换的尺度解析能力。在OPEN GL平台的测试结果表明,该方法的拟合效率高、精度高。
| [1] |
贾萌珊, 齐子元, 薛德庆,等. 基于GASA-BP-BiLSTM的轴承故障预测研究[J]. 组合机床与自动化加工技术, 2023(5): 148−151+155. JIA Meng-shan, QI Zi-yuan, XUE De-qing, et al. Research on bearing failure prediction based on GASA-BP-BiLSTM[J]. Combined Machine Tool and Automatic Processing Technology, 2023(5): 148−151+155. |
| [2] |
ZHU Fu-ping, QIN Qin, YANG Fang-yan, et al. Rolling bearing failure prediction method based on information fusion technology[J]. Mechanical Design, 2023, 40(1): 56-64. |
| [3] |
刘桂然. 基于BP-神经网络的风电主轴承故障预测[J]. 科学技术创新, 2020(26): 18-19. LIU Gui-ran. Fault prediction of main bearing of wind power based on BP-neural network[J]. Science and Technology Innovation, 2020(26): 18-19. |
| [4] |
李泓洋, 万烂军, 李长云, 等. 基于神经网络和证据理论的滚动轴承故障预测方法[J]. 湖南工业大学学报, 2020, 34(4): 35-41. LI Hong-yang, WAN Lan-jun, LI Chang-yun, et al. Rolling bearing failure prediction method based on neural network and evidence theory[J]. Journal of Hunan University of Technology, 2020, 34(4): 35-41. DOI:10.3969/j.issn.1673-9833.2020.04.006 |
 2023, Vol. 45
2023, Vol. 45
