导管架基础是目前海上风电场主要基础型式之一,适用于35~50 m水深。导管架架腿主要通过圆柱壳焊接组成,在风机正常工作状态下导管架架腿承受上部结构传递的载荷作用下,屈曲是其主要失效模式之一。而风机正常工作状态下,载荷随着风向的变化不断发生改变,使得导管架架腿承受循环往复的变化载荷作用,容易造成导管架架腿产生疲劳损伤,因此在对导管架基础进行分析时,不仅要考虑结构的屈服及屈曲强度是否满足规范要求,同样要考虑结构的疲劳强度是否满足规范要求。
目前国内外对圆柱壳屈曲失效的研究相对比较成熟,王黎辉等[1]采用弧长法对不同高度下柱形壳的非线性屈曲行为进行了研究,得出高度越小,越容易在柱壳两端发生变形的结论。陈斌斌[2]采用Abaqus软件对环肋及无肋圆环壳的非线性屈曲研究表明,环肋圆柱壳主要为局部失稳破坏,无肋圆柱壳多为总体失稳破坏。武行等[3]通过对非对称局部壁厚海底管道的屈曲分析研究表明,局部腐蚀对管道的屈曲压力有重要影响。刘桢[4]采用Ls-dyna软件研究了凹陷半径、凹陷深度和凹陷位置对球冠状碰撞凹陷耐压壳临界屈曲载荷的影响。余建星等[5]采用动态加载的方式对不同凹坑深度及凹坑宽度的海底管道进行了局部屈曲模拟;Bardi[6-7]对径厚比在23~52之间的轴压柱形钢管的塑性屈曲性能进行了试验和理论分析;FWei Wang等[8]对比了不同径厚比对轴压圆柱壳临界屈曲载荷的影响;Yujin Wang等[9]采用试验的方法对一种新型铝合金材料进行了屈曲分析,并与现行几种结构设计手册预测的屈曲强度进行了对比。目前很多学者对完整圆柱形壳结构进行了特征屈曲及非线性屈曲的分析研究,得出了相对比较成熟的观点及数值分析方法,但对碰撞产生非规则凹陷后的圆柱形壳屈曲承载能力及疲劳强度的研究还相对比较缺乏。
本文以某导管架架腿在受台风影响发生碰撞凹陷为基础,对比分析碰撞凹陷对导管架架腿屈曲承载能力及疲劳强度的影响,为碰撞产生非规则凹陷圆管的进一步研究及碰撞凹陷后圆管的修复提供参考。
1 有限元模型 1.1 结构几何模型按照现场测绘反馈的信息,导管架架腿碰撞产生的凹陷深度为150 mm,凹陷长度为1 800 mm,凹陷宽度为1 200 mm。架腿初始尺寸:厚度为35 mm,直径为1 600 mm。根据图纸及凹陷区域的尺寸,分别建立导管架基础完整模型及碰撞凹陷模型,其中凹陷位置位于斜撑与导管架架腿第二交点下方,对于完整导管架基础模型,采用凹陷边界将导管架架腿进行分割,以便于计算结果的对比分析。导管架基础、子模型(子模型圆管长7 450 mm)及局部凹陷(以下用凹陷圆管表示)的示意图如图1所示。

|
图 1 有限元结构几何模型 Fig. 1 Structure model |
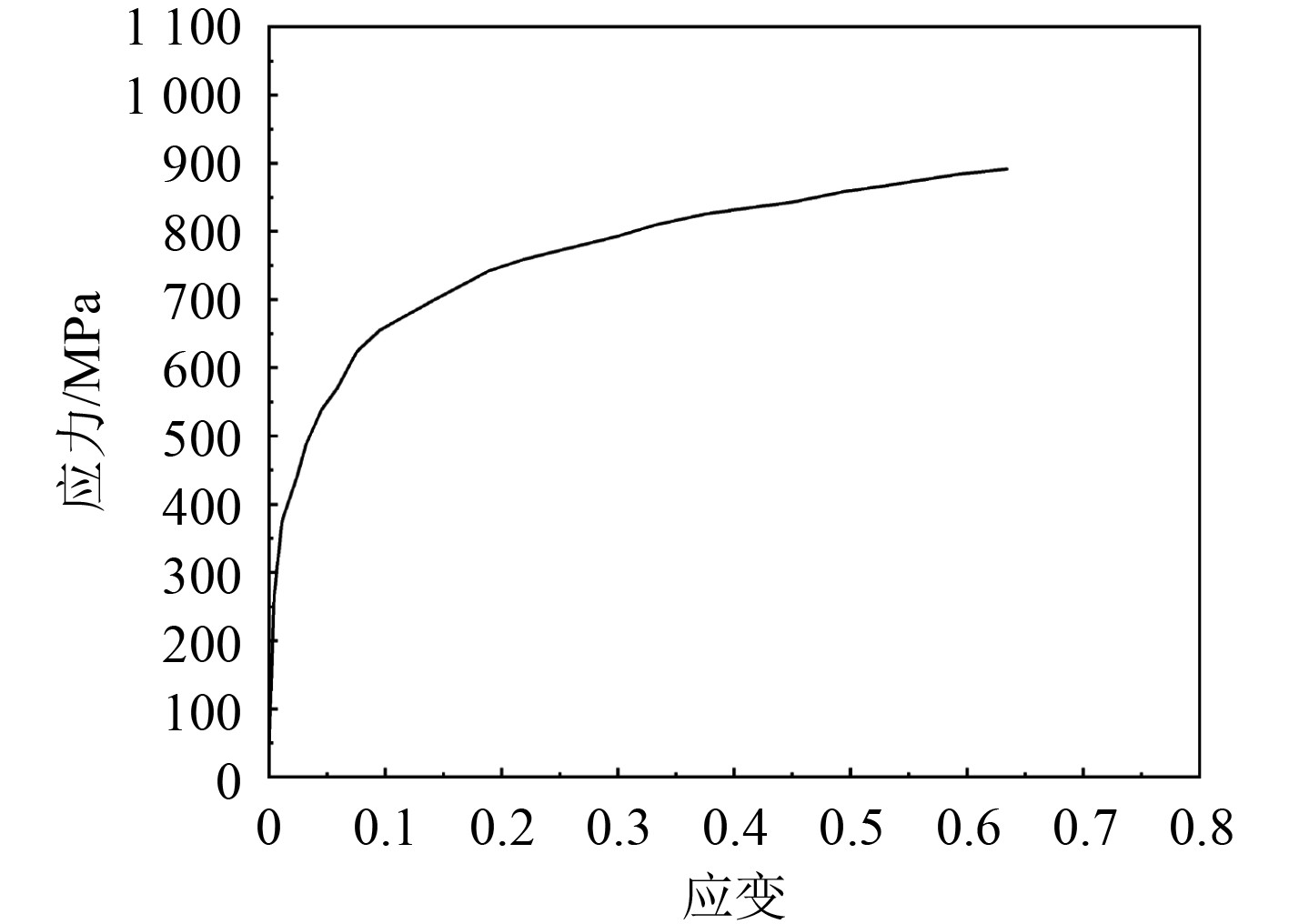
导管架架腿材料采用DH36钢材,其基本材料属性参数:弹性模量为2.1×105 MPa,屈服强度为355 MPa,泊松比为0.3,应力-应变曲线如图2所示[10]。
|
图 2 DH36钢应力-应变曲线图 Fig. 2 The stress-strain curve of DH36 |
考虑计算效率,导管架基础结构模型采用壳体进行建模。整体模型分析时,过渡段网格尺寸为200 mm×200 mm,导管架尺寸为100 mm×100 mm,网格单元选用SHELL181单元,采用四边形进行网格划分,导管架基础总体网格单元数量为58000。
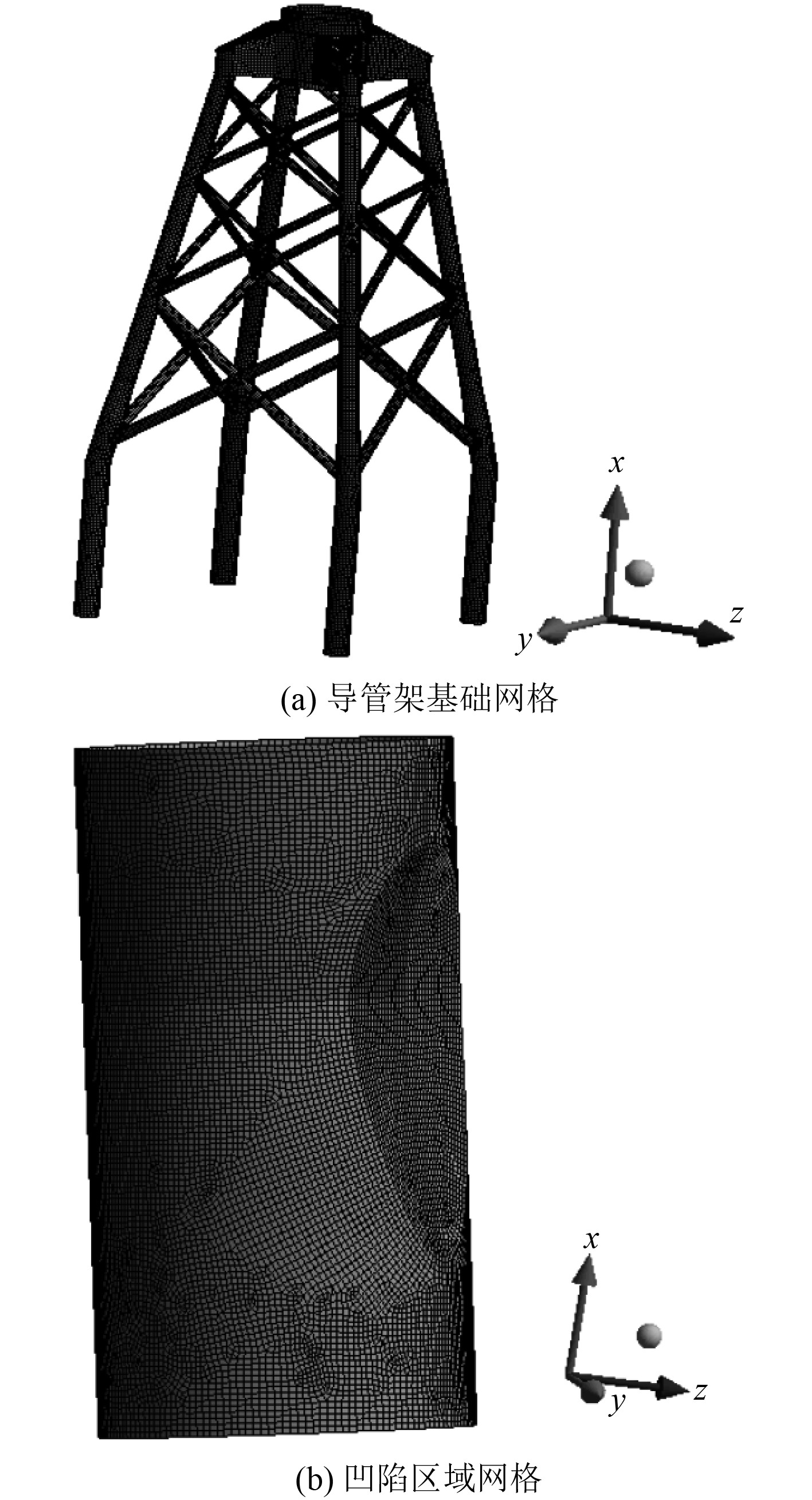
导管架桩腿底部固支,整体模型分析后获取子模型边界,将子模型进行局部网格加密,子模型整体网格尺寸为50 mm×50 mm,凹陷区域网格尺寸为32 mm×32 mm,凹陷圆管网格单元数量为33000。导管架基础及凹陷圆管的网格划分如图3所示。
|
图 3 模型网格划分 Fig. 3 The mesh of jacket model |
圆管在承受轴向载荷作用下,当载荷达到临界载荷时,圆管将发生失稳,因此需要对圆管进行屈曲分析,得到结构的临界屈曲载荷。
对于径厚比
| $ {F_a} = \frac{{\left[ {1 - \dfrac{{{{\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}^2}}}{{2C_c^2}}} \right]{F_y}}}{{{5 \mathord{\left/ {\vphantom {5 {3 + \dfrac{{3\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}}{{8{C_c}}} - \dfrac{{{{\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}^3}}}{{8C_c^3}}}}} \right. } {3 + \dfrac{{3\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}}{{8{C_c}}} - \dfrac{{{{\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}^3}}}{{8C_c^3}}}}}},{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r} < {C_c} ,$ | (1) |
| $ {F_a} = \frac{{12{{\text{π}} ^2}E}}{{23{{\left( {{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r}} \right)}^2}}},{{Kl} \mathord{\left/ {\vphantom {{Kl} r}} \right. } r} \geqslant {C_c} ,$ | (2) |
| $ {C_c} = {\left[ {\frac{{2{{\text{π}} ^2}E}}{{{F_y}}}} \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} 。$ | (3) |
式中:
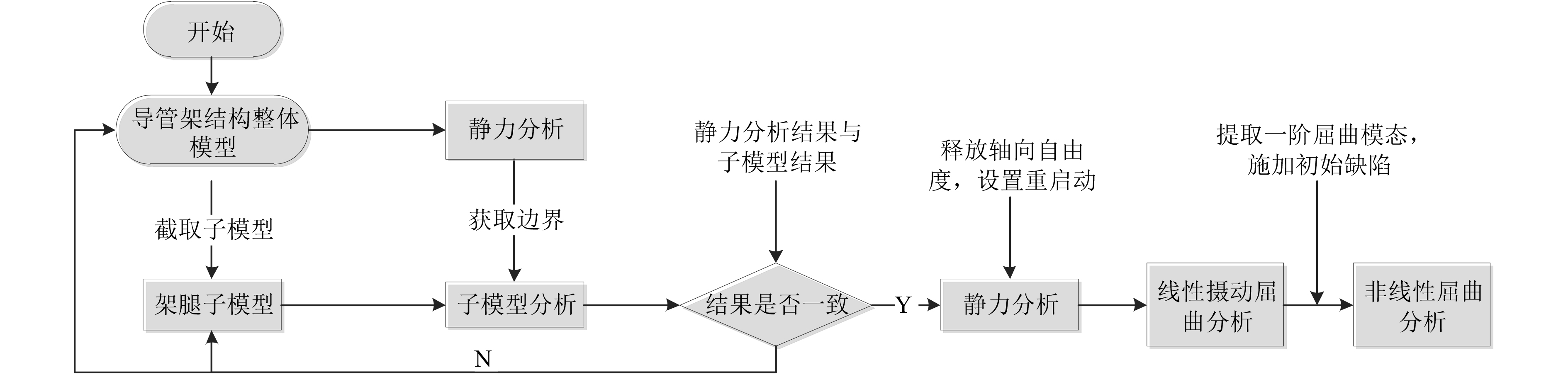
采用Ansys软件对完整圆管及凹陷圆管进行非线性屈曲分析。根据整体模型静力分析结果,提取子模型边界,释放圆管顶部轴向方向的自由度,采用线性摄动分析方法进行特征值屈曲求解一阶屈曲模态,作为非线性屈曲分析的基础,进行非线性屈曲分析,求解流程如图4所示。在进行非线性屈曲分析时需要考虑圆管的初始缺陷,以圆管初始挠度及载荷作用导致的偏心距的和作为缺陷幅值,根据一阶屈曲模态,求出初始缺陷系数[11]。本文初始缺陷系数取0.1,将初始缺陷系数应用到一阶屈曲模态,采用牛顿-辛普森方法进行非线性屈曲分析。
|
图 4 非线性屈曲分析流程图 Fig. 4 The drawing of non-linear buckling analysis |
由表1可知,完整圆管临界屈曲载荷数值模拟与理论计算结果相差3.73%,数值模拟计算结果与理论计算结果吻合较好,可以认为采用该方法计算比较可靠。
|
|
表 1 理论及数值模拟结果临界屈曲载荷 Tab.1 The buckling load of theory and numerical |
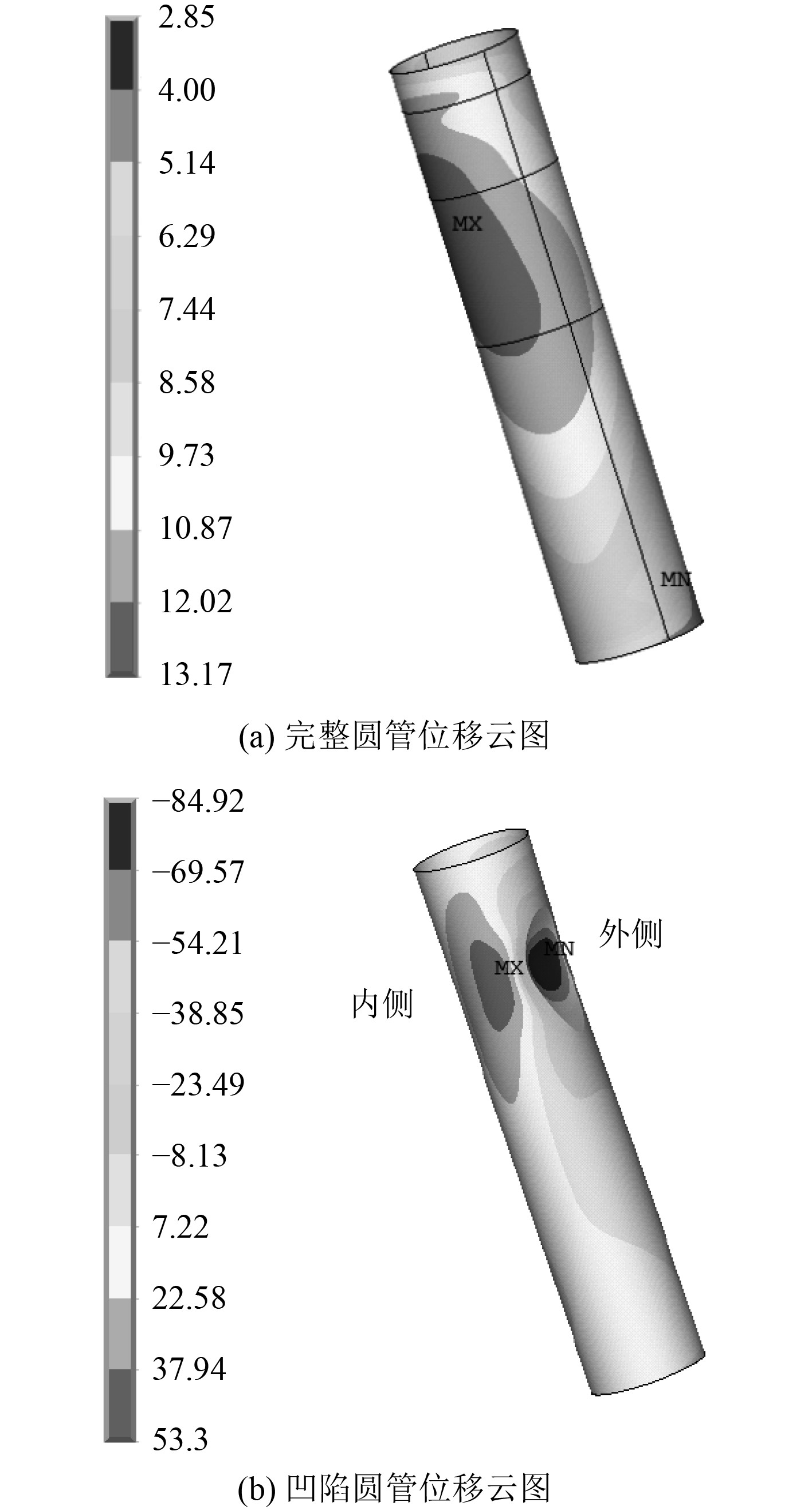
由图5临界屈曲载荷时的径向位移云图可知,在承受顶部轴向载荷作用下,由于子模型边界圆管顶部及底部的各节点约束条件不同,圆管径向位移内侧与外侧变化规律存在明显差异。通过对比图5(a)和图5(b)可知,碰撞凹陷后,在承受轴向载荷作用下,凹陷区域外侧径向位移向内发生凹陷,而凹陷区域内侧径向位移沿径向向外鼓曲。在一定轴向载荷作用下,凹陷圆管产生偏心效应,使得圆管承受弯矩作用,凹陷圆管外侧区域向内发生凹陷,圆管内侧区域向外发生鼓曲的现象更加严重。
|
图 5 圆管位移云图 Fig. 5 The displacement contour of circular tube |
图6(a)为A、B、C、D四点位置处完整圆管载荷与圆管径向位移曲线图。可知,屈曲过程中,载荷随着圆管径向位移呈线性逐渐升高,在达到临界载荷后,载荷-位移曲线斜率变得平缓,完整圆管临界屈曲载荷为3.75×107 N。
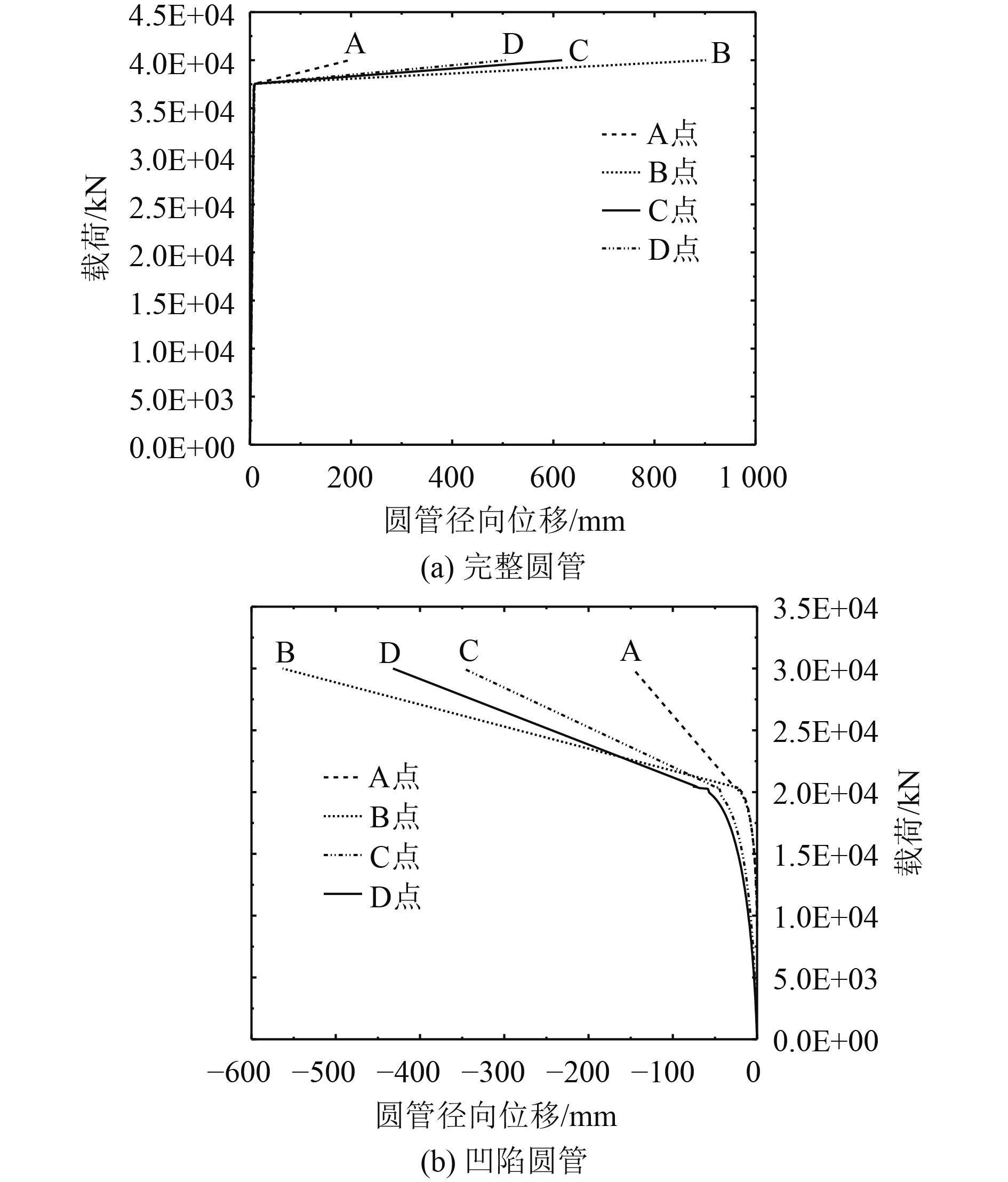
|
图 6 圆管载荷-位移曲线图 Fig. 6 The load-displacement curve of circular tube |
同样由图6(b)A、B、C、D四点位置处凹陷圆管载荷与圆管径向位移曲线图可知,屈曲过程载荷随着圆管径向位移呈近似线性逐渐升高,在达到临界载荷后,载荷-位移曲线斜率变缓,凹陷圆管屈曲临界载荷为2.08×107 N。
由图6可知,不同位置载荷-位移曲线屈曲后变化速率有所差异。达到临界屈曲载荷后,完整圆管C、D点载荷-位移曲线斜率基本保持一致,但C、D点位置最大位移不同。完整圆管C点位置最大位移为618 mm,D点位置最大位移为506 mm;凹陷圆管C点位移最大值为−432 mm,D点最大位移为−348 mm。造成C、D点位移不一致的原因是子模型边界从整体模型分析获取各节点的位移及转动自由度不同;而碰撞凹陷后,C、D点载荷-位移曲线斜率略有不同,原因是碰撞凹陷导致圆管在轴向载荷作用下发生了偏心效应。以C、D点为例(A、B点同理),达到临界屈曲载荷后,通过对比圆管碰撞凹陷前后C、D点的载荷-位移曲线的变化可知,完整圆管C、D点载荷-位移曲线斜率更加的平缓。对于碰撞凹陷后的圆管,在产生相同径向位移变化时,需要更大的轴向载荷的变化量,说明碰撞凹陷后圆管的延展性有所提高。
3 圆管疲劳分析 3.1 疲劳计算理论与方法基于Miner线性累积损伤理论的S-N曲线法进行计算分析。根据DNV-RP-C203规范[12],疲劳安全系数取3,S-N曲线选取海水中自由腐蚀阴极保护的D-Curve进行疲劳分析校核,S-N曲线数学表达式为:
| $ \log N = \log \overline a - m\log \left( {\Delta \sigma {{\left( {\frac{t}{{{t_{ref}}}}} \right)}^k}} \right) 。$ | (4) |
式中:
根据表2所示风向概率分布,25年风机载荷作用下疲劳循环次数为1×108 ,考虑16个方向的风机载荷激励,采用热点应力法提取单元最大主应力计算等效疲劳。对计算敏感区域,按照DNV-RP-C203规范要求,网格密度尺寸约等于板厚,采用32 mm×32 mm的网格尺寸。本文主要关注区域为导管架架腿凹陷处的疲劳损伤,因此对于其他区域的疲劳不再进行校核。
|
|
表 2 风向概率分布表 Tab.2 The wind direction probability distribution |
由图7可知,在不考虑疲劳安全系数情况下,完整圆管整体疲劳损伤分布比较均匀,疲劳损伤值的范围为0.02~0.03。而发生碰撞凹陷后,凹陷区域圆管疲劳损伤值发生显著变化,疲劳损失值范围为0.002~0.38。碰撞凹陷后图中E、F、G、H区域的疲劳损失值相对降低。由文献[13]可知,对于凹陷区域其中间凹痕及凹陷边界起主要承受外载荷作用。在承受轴向载荷作用下,凹陷区域发生挤压,导致该处应力分布不均匀,中间凹痕及凹陷边界处产生应力集中,而凹陷上部中心区域E及凹陷下部区域F受力较小(同理,G、H区域疲劳损失值较相邻其他区域疲劳损失值低),从而造成中间凹痕及凹痕边界处的疲劳损失值较其他区域损失值高。
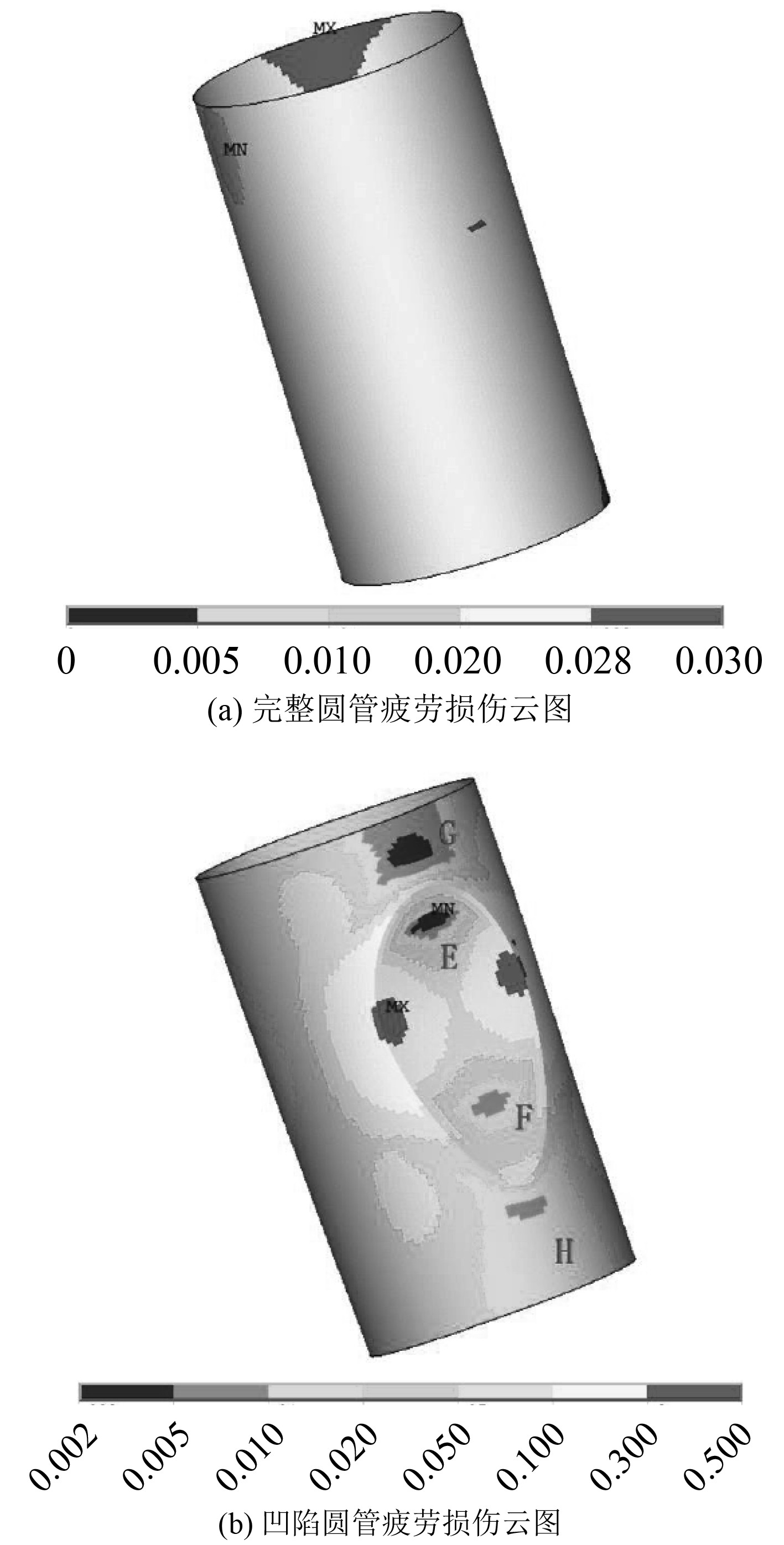
|
图 7 圆管疲劳损伤云图 Fig. 7 Fatigue damage contour of circular tube |
由图8可知,对于完整圆管,其疲劳损伤值在凹陷边界处由C1-A1点呈现先平缓增加,在A1点区域附近疲劳损伤快速增加;由A1~D1点,疲劳损伤整体呈现下降趋势;由D1~B1点,同样呈现整体下降趋势,下降趋势比较平缓,疲劳损失值相差不大(3‰以内),但在靠近B1点附近疲劳损伤值升高;B1~C1点,呈现先下降后上升的趋势。完整圆管在A1和B1点出现极值,疲劳损伤最大值出现在A1点,为0.0167,但完整圆管凹陷边界整体疲劳损伤变化率不大(7‰以内)。
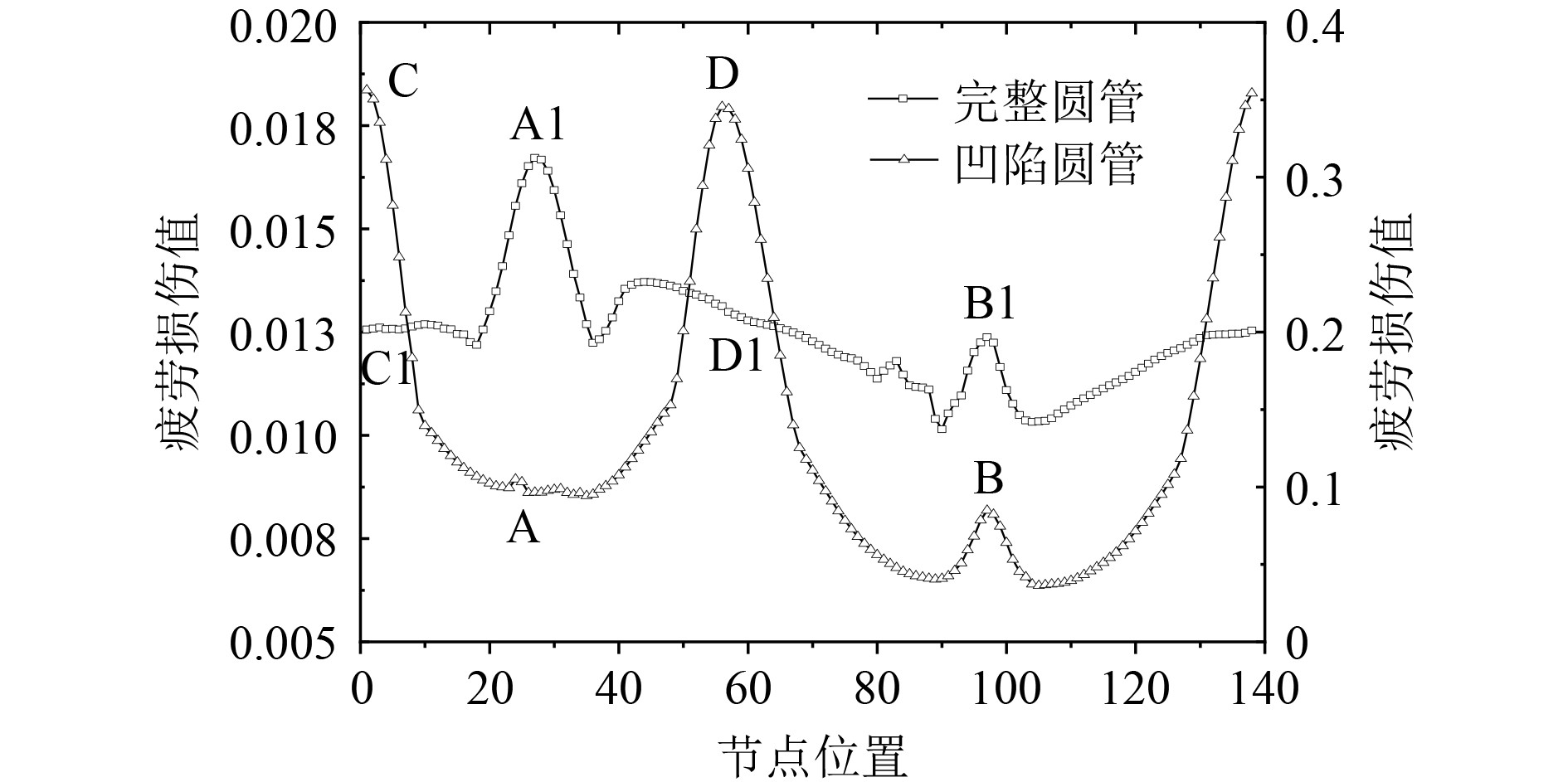
|
图 8 凹陷边界疲劳损伤曲线图 Fig. 8 Fatigue damage curve of depression edge |
而对于凹陷圆管,C-A-D-B-C边界上,B-C-A与B-D-A疲劳损伤值近似对称,因此仅分析B-C-A边界上疲劳损伤变化趋势。疲劳损伤值由B-C点,在靠近B附近,疲劳损伤值先呈下降趋势,远离B点后,疲劳损伤值呈指数倍增长。而疲劳损伤值由C-A点,先快速降低,在靠近A点附近疲劳损伤值逐渐平缓。凹陷圆管边界上最大损伤值出现在C、D位置处即(中间凹痕与凹陷边界的交点处),疲劳损伤最大值为0.376,在凹陷底部出现极值点B,疲劳损伤值为0.085。对于凹陷圆管凹陷边界不同位置处的疲劳损伤值变化率较大,凹陷边界上疲劳损伤变化率达3.4%。
4 结 语以某海上风电场导管架基础的架腿在受台风影响下与运维船发生碰撞凹陷为基础,采用Ansys软件对碰撞产生凹陷后的圆管屈曲承载能力及疲劳强度进行研究,根据计算结果得出如下主要结论:
1)在轴向载荷作用下,碰撞凹陷会导致圆管的屈曲承载能力降低,本文圆管发生碰撞凹陷后,屈曲承载能力降低了45.87%。
2)完整圆管在轴向临界屈曲载荷作用下,圆管径向位移沿圆管径向发生鼓曲;凹陷圆管由于发生偏心效应,导致圆管径向位移局部呈沿圆管径向向内凹陷和向外鼓曲的现象。
3)碰撞凹陷后,凹陷区域圆管应力发生重分布,中间凹痕及凹陷边界起主要承受载荷的作用,疲劳损失值较大。
4)碰撞凹陷后,圆管凹陷边界上的疲劳损伤值显著增加,且最大疲劳损伤区域由顶部A点区域转移至凹陷圆管中间凹痕的C、D点区域。凹陷边界上,疲劳损失值呈现从中间凹痕处(C、D点)向凹陷顶部(A点)及底部(B点)逐渐降低的趋势,并且在凹陷底部B点区域疲劳损伤值局部升高。
| [1] |
王黎辉, 李其凡, 张建等. 轴压柱形壳非线性屈曲试验与理论研究[J]. 船舶力学, 2021, 25(5): 645–651. WANG Li-hui, LI Qi-fan, ZHANG Jian et al. Experimental and theoretical study on nonlinear bucklingof axially compressed cylindrical shells[J]. Journal of Ship Mechanics, 2021, 25(5): 645–651. |
| [2] |
陈斌斌. 圆环耐压壳屈曲特性及试验研究[D]. 镇江: 江苏科技大学, 2019.
|
| [3] |
武行, 赵海盛, 李昕等. 非对称局部壁厚减薄海底管道的屈曲分析[J]. 海洋工程, 2021, 39(3): 72–82. WU Hang, ZHAO Haisheng, LI Xin. Buckling analysis of pipes with asymmetric local wall thinning[J]. The Ocean Engineering, 2021, 39(3): 72–82. |
| [4] |
刘桢. 考虑碰撞凹陷的钛合金耐压壳屈曲研究[D]. 镇江: 江苏科技大学, 2020.
|
| [5] |
余建星, 薛陆丰, 余扬等. 动态加载模拟凹坑对管道模型压溃影响[J]. 天津大学学报, 2018, 51(7): 667–674. YU Jianxing, XUE Lufeng, YU Yang et al. Influence of denting under dynamic loading on subsea pipeline buckling[J]. Journal of Tianjin University(Science and Technology), 2018, 51(7): 667–674. |
| [6] |
BARDI F C, Kyriakides. S. Plastic buckling of circular tubes under axial compression partⅠ: Experiments[J]. International Journal of Mechanical Sciences, 2006, 48(8): 830–841.
|
| [7] |
BARDI F C, KYRIAKIDES S. Plastic buckling of circular tubes under axial compression part Ⅱ: Analysis[J]. International Journal of Mechanical Sciences, 2006, 48(8): 842–854.
|
| [8] |
WANG Wei, QIU XinMing. An analytical study for global buckling of circular tubes under axial and oblique compressiong[J]. International Journal of Mechanical Sciences, 2017, 17: 120-129. |
| [9] |
WANG Yujin, FAN Feng, LIN Shibin. Experimental investigation on the stability of aluminium alloy 6082 circular tubes in axial compression[J]. Thin-Walled Structures, 2015, 89: 54-66. DOI:10.1016/j.tws.2014.11.017 |
| [10] |
郭伟国, 史飞飞, 刘风亮. 高强度船体结构钢DH36的动态力学性能研究[C]// 第九届全国冲击动力学学术会议论文集. 2009. GUO Weiguo, SHI Feifei, LIU Fengliang. Investigation on Dynamic Mechanical Performances of DH36 High Strength Shiphull Steel[C]// The 9th National Conference on Impact Dynamics. 2009. |
| [11] |
SHI Gang, JIANG Xue, ZHOU Wenjing, et al. Experimental study on column buckling of 420 MPa high strength steel welded circular tubes[J]. Journal of Constructional Steel Research, 2014, 100: 71-81. DOI:10.1016/j.jcsr.2014.04.028 |
| [12] |
DNVGL-RP-C203Fatiguedesignofoffshoresteelstructures[S]. DNVGL. 2020.
|
| [13] |
孔杰灵. 导管架平台管状构件碰撞受损后的剩余强度研究[D]. 武汉: 武汉理工大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
