潜艇的工作海域通常深度大、地形复杂,一旦发生碰撞事故可能会造成难以预测的后果,因此,防护潜艇受到的碰撞冲击作用成为重要的研究课题。当前防护碰撞冲击作用主要基于能量耗散理论,即通过结构的变形吸收冲击作用的能量,常规材料已逐渐无法满足防护需求。五模材料作为一种新型超材料,兼具流体和固体的特性,通过对五模材料的设计,可实现对应力波的调控,可为潜艇的碰撞防护提供新的解决方法。
1995年,Milton等[1]首次提出了五模材料的概念,其弹性刚度矩阵的6个特征值仅有一个不为0,即只能承受一种应力状态。理想五模材料的剪切模量为0,但出于实际使用需要,会保留一定的抗剪强度。Milton等[2]研究了弹性动力学方程的空间坐标变换,理论上通过设计材料的弹性模量,可以实现弹性波的隐身。Norris[3]在弹性波坐标变换理论基础上,提出了五模材料声学隐身斗篷设想,该斗篷可以弯曲声波的传播路径,使目标物体在声场中“消失”。Scandrett等[4,5]证明了使用分层五模材料构建声学斗篷的可行性,使坐标变换理论突破了连续变化各向异性材料的限制,为声学隐身斗篷的实现提供了可能。Zafiris等[6]通过仿真研究了一种基于层状杆结构的五模材料,发现其在一定频率范围内接近理想五模材料,可以有效调控声波,在弹性动力学领域有广阔的应用前景。Layman等[7]提出了一种基于二维蜂窝结构的五模材料,通过仿真发现其具有良好的声波调控能力,将五模材料从三维结构简化为二维结构,极大降低了制作难度。Tian等[8]提出并通过仿真计算了一种基于二维五模材料的声学超表面结构,通过五模材料胞元排布形成速度梯度,产生相位延迟,使声波折射按照预想角度折射,以达到调控声波的目的,在宽带波的调控方面有广阔的应用前景。Chen等[9]设计了一种由单相固体材料制成的五模声学斗篷,用数值方法验证了声波的绕射效果,但由于弱剪切模量引起的共振导致了该斗篷仅在部分频率范围内有隐身效果。Li等[10]设计了一种五模球形声隐身斗篷,研究发现五模材料的各向异性越强,调控效果越好。
当前五模材料在应力波调控领域的应用主要集中于声学隐身,在其他领域的应用潜力,如冲击隐身、静力隐身、减振隔振等方面,还未被有效发掘,仅有少数学者在开展相关研究,并且尚处于起步阶段[11-15]。为探索五模点阵环状结构对碰撞冲击波的调控作用,本文设计制作了五模点阵环状结构试验模型,并进行冲击试验及仿真。通过计算胞元频散特性可获得频散曲面等值线的法向量方向分布,并在此基础上研究其与能流矢量的联系,相关结论可为五模材料在碰撞冲击防护领域的应用提供一定的理论支撑。
1 五模点阵环状结构设计制作 1.1 五模点阵环状结构设计理论 1.1.1 坐标变换理论波传播动力学过程由的程描述为:
| $ \left\{\begin{aligned}&\sigma =-p{\boldsymbol{S}},\\& \rho \cdot \dot{v}=\nabla \cdot \sigma 。\end{aligned}\right. $ | (1) |
由此可以得到
| $ \left\{\begin{aligned}&k{\boldsymbol{S}}={k}_{0}{\rm{det}}{\boldsymbol{AP}},\\&{\rho }^{-1}S={\rho }_{0}^{-1}\dfrac{{P}^{-1}{\boldsymbol{A}}{{\boldsymbol{A}}}^{{\rm{T}}}}{{\rm{det}}{\boldsymbol{A}}}。\end{aligned}\right. $ | (2) |
式中:S、P均为广义对称矩阵;A为变换矩阵;
| $ {r}{'}=\sqrt{\frac{{R}_{2}^{2}-{\delta }^{2}}{{R}_{2}^{2}-{R}_{1}^{2}}{r}^{2}-\frac{{R}_{1}^{2}-{\delta }^{2}}{{R}_{2}^{2}-{R}_{1}^{2}}{R}_{2}^{2}} ,$ | (3) |
| $ {\theta }'=\theta。$ | (4) |
式中:
| $ \rho ={\rho }_{0}\frac{{R}_{2}^{2}-{\delta }^{2}}{{R}_{2}^{2}-{R}_{1}^{2}},$ | (5) |
| $ {k}_{r}={k}_{0}\frac{{r}^{2}\left({R}_{2}^{2}-{\delta }^{2}\right)-({R}_{1}^{2}-{\delta }^{2}){R}_{2}^{2}}{{r}^{2}({R}_{2}^{2}-{\delta }^{2})},$ | (6) |
| $ {k}_{\theta }={k}_{0}\frac{{r}^{2}({R}_{2}^{2}-{\delta }^{2})}{{r}^{2}\left({R}_{2}^{2}-{\delta }^{2}\right)-({R}_{1}^{2}-{\delta }^{2}){R}_{2}^{2}} 。$ | (7) |
式中:
对于胞元形状复杂的微结构,几乎不可能通过解析式求解的方法来获取等效力学参数,因此需要采用数值均质化的方法进行材料等效转化。对于等效材料,通常需要获取其等效密度和等效弹性矩阵。在长波条件下,微结构胞元一般不存在共振现象,因此胞元的等效密度可表示为:
| $ {\rho }^{{e}{f}{f}}={m}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}/{V}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}。$ | (8) |
式中:
| $ \mathit{C}=\left[\begin{array}{ccc}{K}_{{x}}^{{e}{f}{f}}& {K}_{{x}{y}}^{{e}{f}{f}}& 0\\ {K}_{{x}{y}}^{{e}{f}{f}}& {K}_{y}^{eff}& 0\\ 0& 0& {G}_{{x}{y}}^{{e}{f}{f}}\end{array}\right] 。$ | (9) |
将等效弹性矩阵代入动力学方程有:
| $ {C}_{{L}{x}}=\sqrt{{K}_{{x}}^{{e}{f}{f}}/{\rho }^{{e}{f}{f}}} ,$ | (10) |
| $ {C}_{{L}{y}}=\sqrt{{K}_{{y}}^{{e}{f}{f}}/{\rho }^{{e}{f}{f}}},$ | (11) |
| $ {C}_{{T}}=\sqrt{{G}_{{x}{y}}^{{e}{f}{f}}/{\rho }^{{e}{f}{f}}} ,$ | (12) |
| $ \begin{split} {C}_{{q}{L}}^{2}=& \frac{1}{4{\rho }^{{e}{f}{f}}}({K}_{{x}}^{{e}{f}{f}}+{K}_{{y}}^{{e}{f}{f}}+2{G}_{{x}{y}}^{{e}{f}{f}}+\\ & \sqrt{{\left({K}_{{x}}^{{e}{f}{f}}-{K}_{{y}}^{{e}{f}{f}}\right)}^{2}+{4({K}_{{x}{y}}^{{e}{f}{f}}+{G}_{{x}{y}}^{{e}{f}{f}})}^{2}}),\end{split} $ | (13) |
| $ \begin{split} {C}_{{q}{T}}^{2}=& \frac{1}{4{\rho }^{{e}{f}{f}}}({K}_{{x}}^{{e}{f}{f}}+{K}_{{y}}^{{e}{f}{f}}+2{G}_{{x}{y}}^{{e}{f}{f}}-\\ & \sqrt{{\left({K}_{{x}}^{{e}{f}{f}}-{K}_{{y}}^{{e}{f}{f}}\right)}^{2}+{4({K}_{{x}{y}}^{{e}{f}{f}}+{G}_{{x}{y}}^{{e}{f}{f}})}^{2}})。\end{split} $ | (14) |
式中:
| $ {K}_{{x}}^{{e}{f}{f}}={\rho }^{{e}{f}{f}}{C}_{{L}{x}}^{2},$ | (15) |
| $ {K}_{{y}}^{{e}{f}{f}}={\rho }^{{e}{f}{f}}{C}_{{L}{y}}^{2} ,$ | (16) |
| $ {G}_{{x}{y}}^{{e}{f}{f}}={\rho }^{{e}{f}{f}}{C}_{{T}}^{2},$ | (17) |
| $ {K}_{{x}{y}}^{{e}{f}{f}}={\rho }^{{e}{f}{f}}(\sqrt{{\left({C}_{{q}{L}}^{2}-{C}_{{q}{T}}^{2}\right)}^{2}-{({C}_{{L}{x}}^{2}-{C}_{{L}{y}}^{2})}^{2}/4}-{C}_{{T}}^{2})。$ | (18) |
通过胞元频散曲面可获取胞元各个方向的相速度,在此基础上可获取胞元等效弹性矩阵,实现复杂微结构的数值均质化。
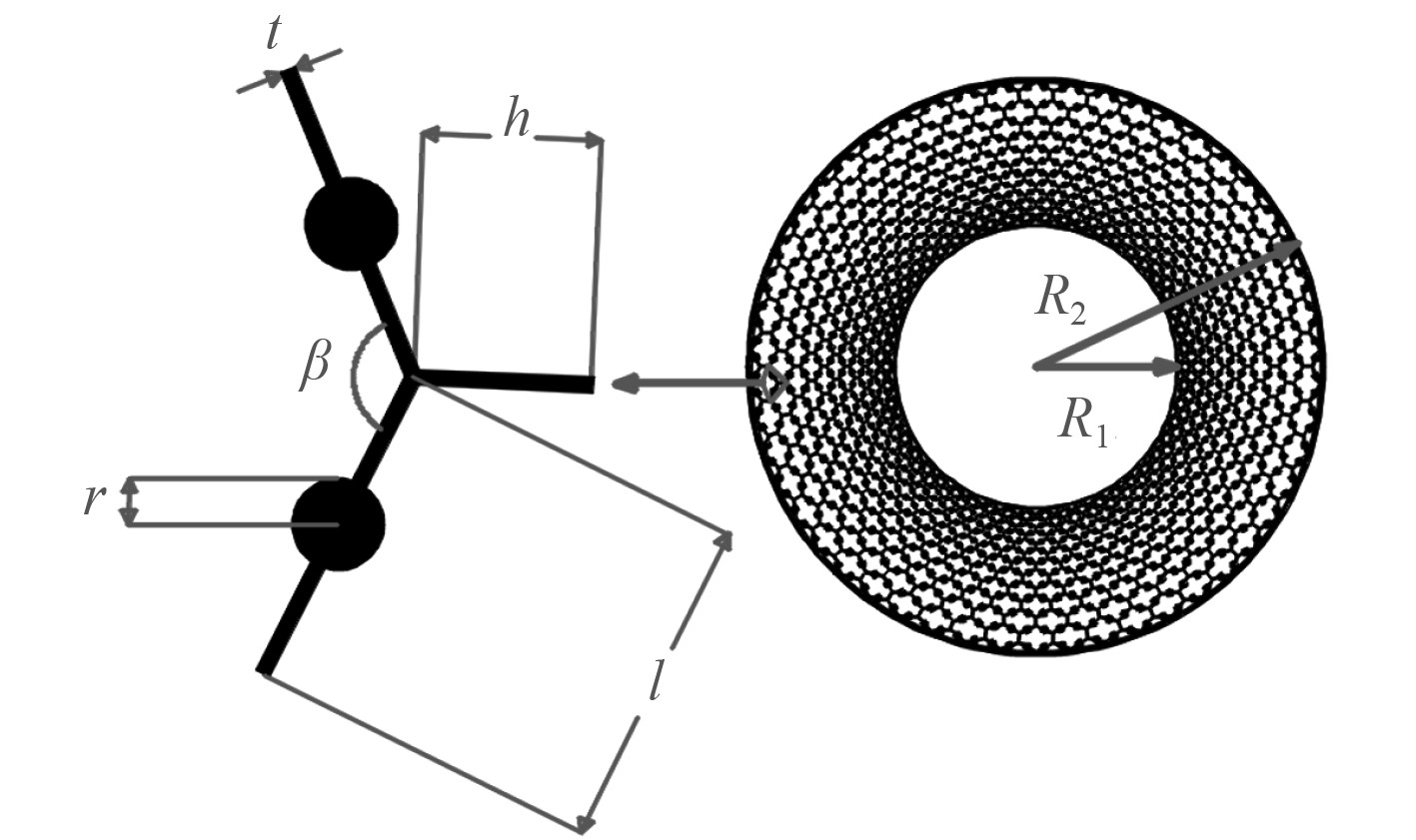
1.2 五模点阵环状结构设计制作基于坐标变换理论,可获取理想五模点阵环状结构的材料参数分布。在此基础上,设计各层胞元结构尺寸,使其等效参数基本满足坐标变换的要求。采用增材制造技术制作出实物模型,圆环内半径R1=45 mm;外半径R2=95 mm;壁厚t=0.65 mm;基材选用PC材料,其材料参数为:弹性模量E=2 000 MPa,密度ρ=1 200 kg/m3,泊松比ν=0.4。五模点阵环状结构各层胞元尺寸及等效参数如图1及表1所示。定量刻画所设计材料与理想五模材料的近似程度主要由以下指标确定:
|
图 1 五模点阵环状结构图 Fig. 1 Diagram of pentamode lattice ring structure |
|
|
表 1 五模点阵环状结构参数、等效参数及五模特征参数 Tab.1 Pentamode lattice ring structure parameters, equivalent parameters and pentamode characteristic parameters |
| $ \pi =\frac{\left|{K}_{{x}{y}}^{{e}{f}{f}}\right|}{\sqrt{{K}_{{x}}^{{e}{f}{f}}{K}_{{y}}^{{e}{f}{f}}}} ,$ | (19) |
| $ \mu =\frac{{G}_{{x}{y}}^{{e}{f}{f}}}{\sqrt{{K}_{{x}}^{{e}{f}{f}}{K}_{{y}}^{{e}{f}{f}}}} 。$ | (20) |
理想五模材料的特征指标为π=1和µ=0,此时材料既有固体的性质,又有流体的性质,但实际情况中π=1和µ=0无法实现,只能趋向于1和0。由表1不难发现,斗篷外层胞元五模特征参数明显优于内层胞元,这主要是受制作工艺的限制,内层胞元的杆件长细比过大,从而降低了内层胞元的五模特性。
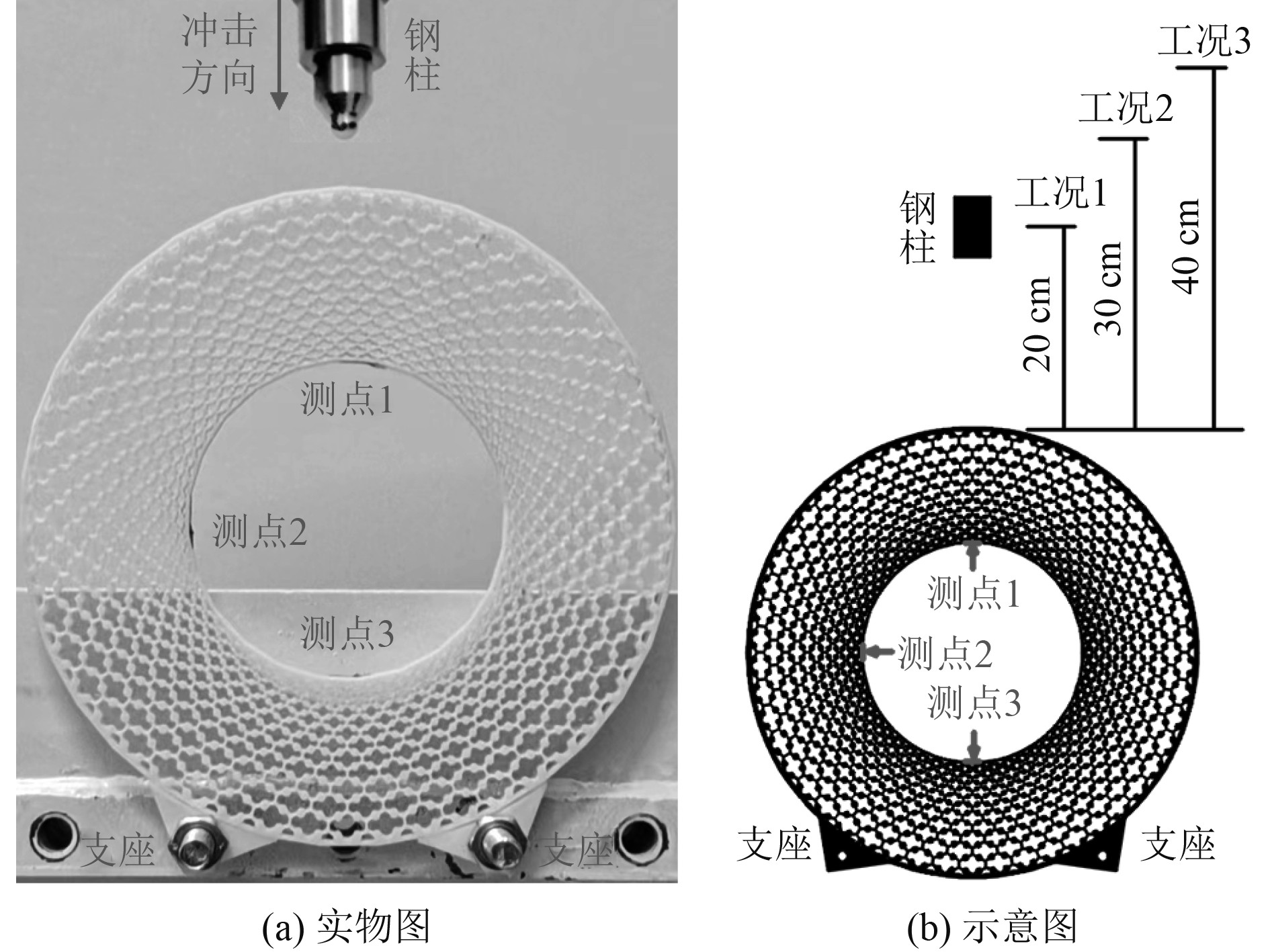
2 五模点阵环状结构冲击试验 2.1 试验工况在五模点阵环状结构内环选取3个测点分别位于顶部(迎冲面)、侧部及底部(背冲面),在3个测点处沿环向各粘贴1枚应变片。利用螺栓将支座连同试验模型固定于铁架上,将1个50 g钢柱分别置于试验模型正上方20 cm、30 cm、40 cm高度处,分别对应工况1、工况2、工况3,使钢柱由静止自由落体对试验模型进行碰撞冲击,试验装置如图2所示。
|
图 2 试验装置图 Fig. 2 Experimental device |
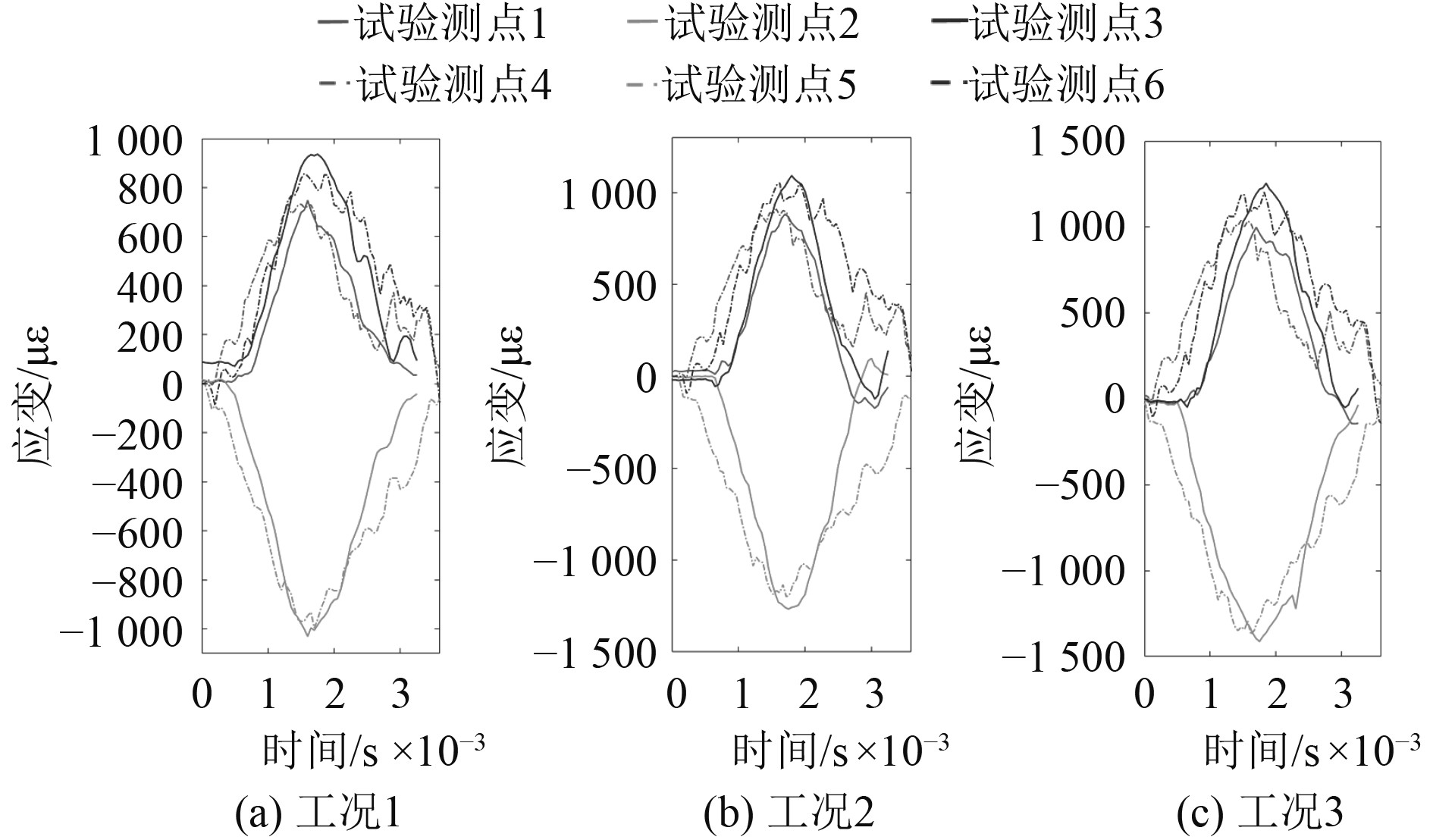
选取3个测点应变峰值段试验数据,并3个工况的应变时程曲线图,如图3所示。各测点的应变峰值大小,如表2所示。
|
图 3 五模点阵环状结构应变时程曲线 Fig. 3 Strain time history curve of pentamode lattice ring structure |
|
|
表 2 试验及仿真测点应变峰值 Tab.2 Peak strain of test and simulation measuring points |
不同工况下的冲击试验中,五模点阵环状结构的
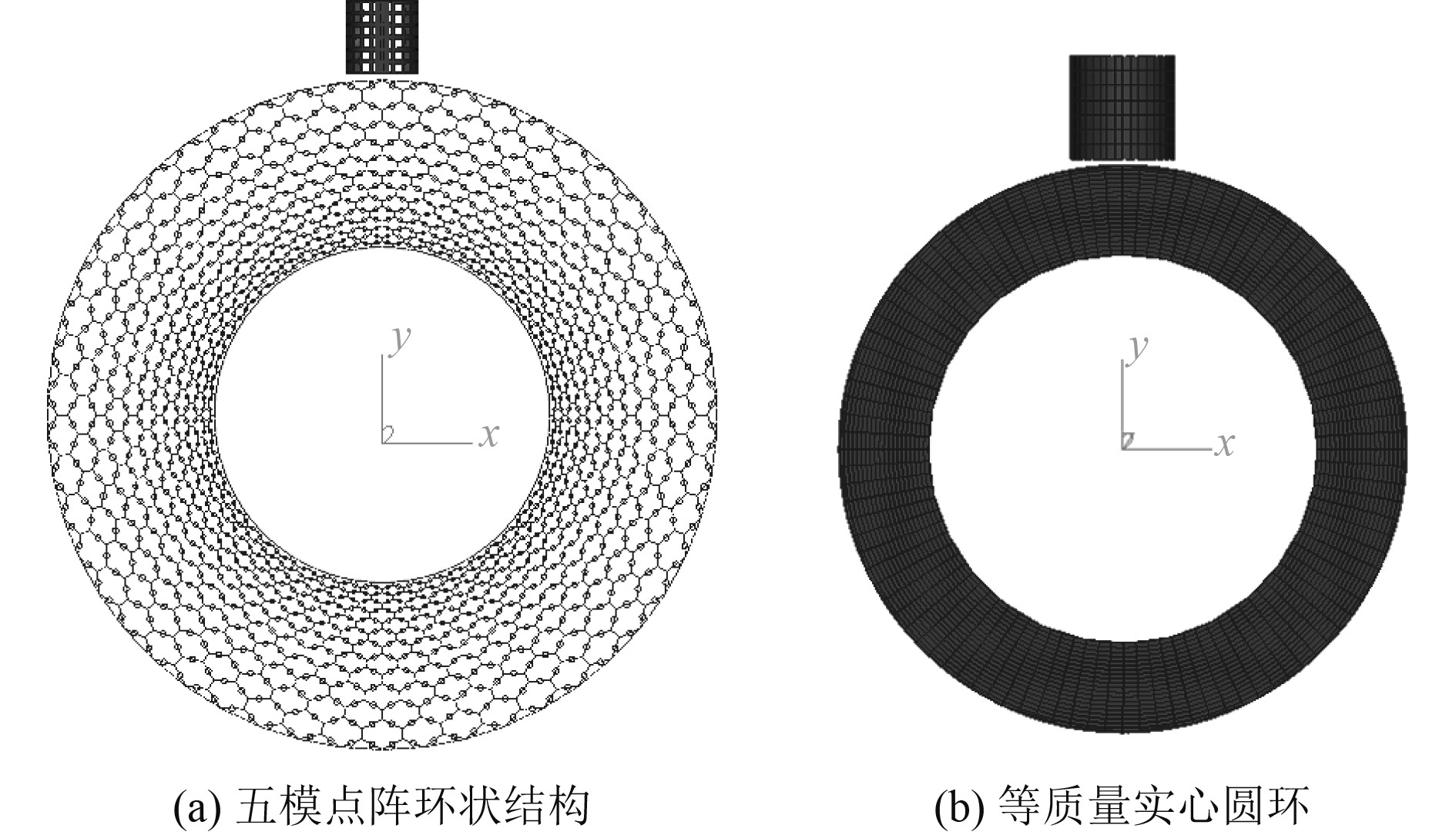
利用MSC.Patran软件对五模点阵环状结构进行前处理建模,为凸显五模点阵环状结构的防护性能,建立一个等质量实心圆环作为参照,2个有限元模型的仿真工况同试验工况完全一致,等质量实心圆环的内半径同五模点阵环状结构内半径相等,如图4所示。
|
图 4 Patran建模示意图 Fig. 4 Schematic diagram of Patran modeling |
通过MSC.Dytran软件对模型进行后处理计算,并输出3个测点处的应变数据。将五模点阵环状结构的仿真结果同试验结果进行对比,见图3。试验数据同仿真数据十分吻合,2组数据应变峰值误差均在15%以内,仿真
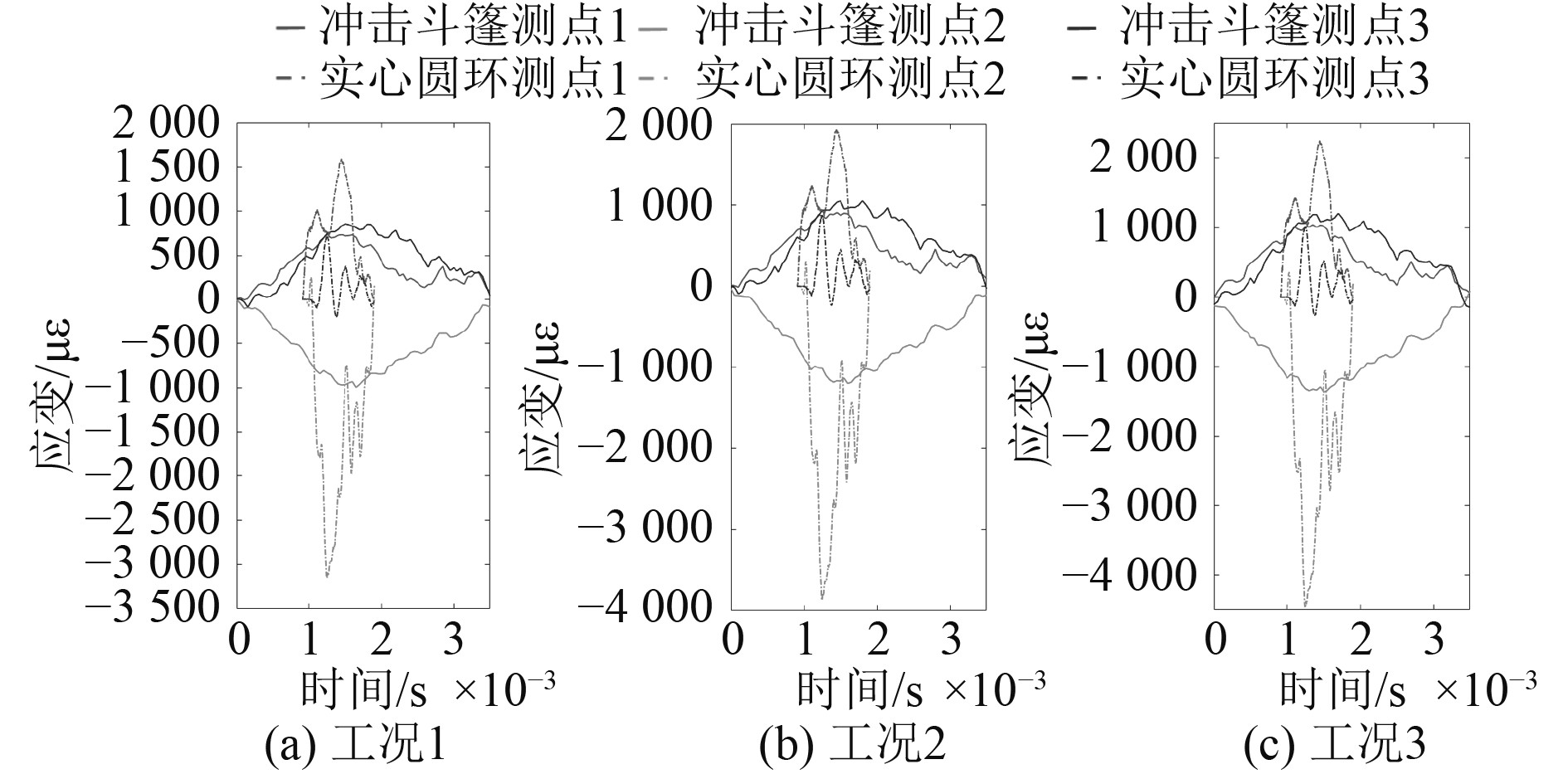
对比等质量实心圆环和五模点阵环状结构的仿真应变结果,如图5所示,实心圆环仿真应变峰值见表2。等质量实心圆环迎冲面的应变峰值明显大于背冲面,其
|
图 5 仿真应变时程曲线 Fig. 5 Simulated strain time history curve |
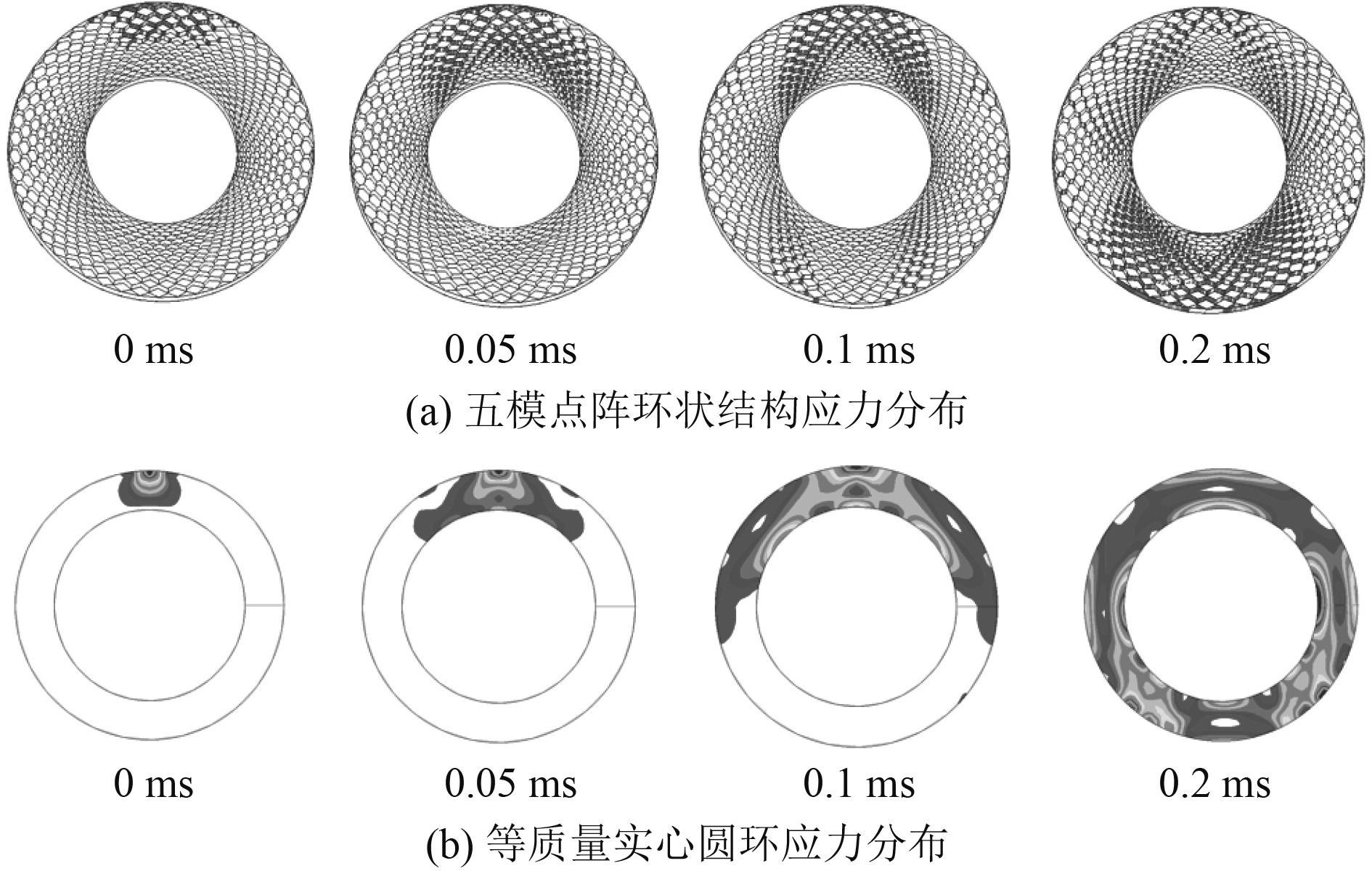
通过MSC.Patran读取计算结果文件可直观看到各时刻模型中的应力分布情况,3个工况下应力分布情况大致相似,现选取工况1的应力分布结果进行分析,如图6所示。
|
图 6 仿真应力分布图 Fig. 6 Simulated stress distribution |
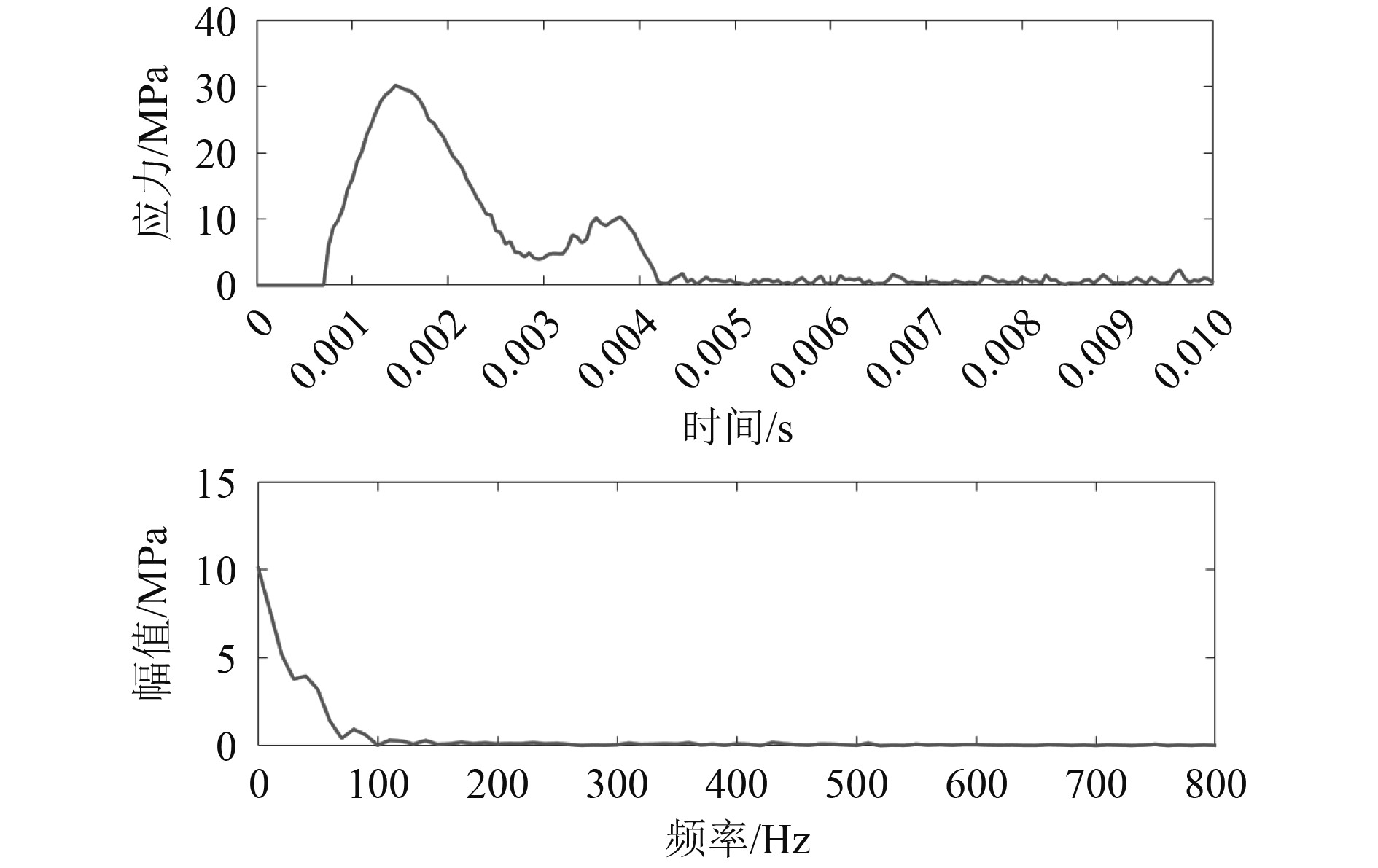
可知,五模点阵环状结构受到碰撞冲击作用后,应力有一向两侧发散的趋势,有效“疏导”了冲击应力波。等质量实心圆环的应力分布则明显不同,在受到碰撞冲击作用后,迎冲面出现了明显的应力集中。因此,五模点阵环状结构可对碰撞冲击作用所产生的应力波进行调控,有效减轻迎冲面的应力集中作用。对五模点阵环状结构和等质量实心圆环撞击点处的应力进行频谱分析,碰撞产生的应力波主要频率范围为0~100 Hz,如图7所示。
|
图 7 碰撞冲击应力频谱分析 Fig. 7 Spectrum analysis of impact stress |
频散曲面决定了群速度的方向和大小,而群速度又是能流矢量的具体体现。因此通过分析五模点阵胞元的频散曲面,可获取能量在结构中的传播特性。频率确定时,频散曲面将退化为等值线,等值线法向量的方向分布反映了该频率下能量传输的主要方向,也就是如果等值线法向量落在某一个传播方向中的幅值越大,则该方向传输的能量就越多。利用COMSOL软件对五模点阵胞元的不可约布里渊区进行扫频,在此基础上可以得到胞元的频散特性,如图8所示。

|
图 8 第13层胞元频散特性 Fig. 8 Dispersion characteristics of the 13th layer cell |
图8(a)为五模点阵环状结构第13层胞元的频散曲面,共计算了前6阶频散曲面,1阶频散曲面为横波频散曲面,2阶频散曲面为纵波频散曲面,其他高阶频散曲面为极高频率下纵波和横波耦合的频散曲面。对于8 000 Hz以下的频率,各层五模点阵胞元的横波波速均小于纵波波速的1/4,根据应力波能量计算公式[16],应力波所蕴含的能量同波速的平方成正比,因此,横波所蕴含的能量不足纵波的1/10,2阶频散曲面是主要研究对象。图8(b)为2阶频散曲面的等值线,不难发现,在8 000 Hz以内,频率的改变对等值线形状几乎无影响,在此基础上计算8 000 Hz以下等值线的法向量,如图8(c)所示,并统计法向量的方向分布,如图8(d)所示。法向量方向分布具有明显的各向异性,存在一个分叉角度
|
|
表 3 五模点阵胞元法向量及机械能流分叉角 Tab.3 Normal vector of pentamode lattice cell and bifurcation angle of mechanical energy flow |
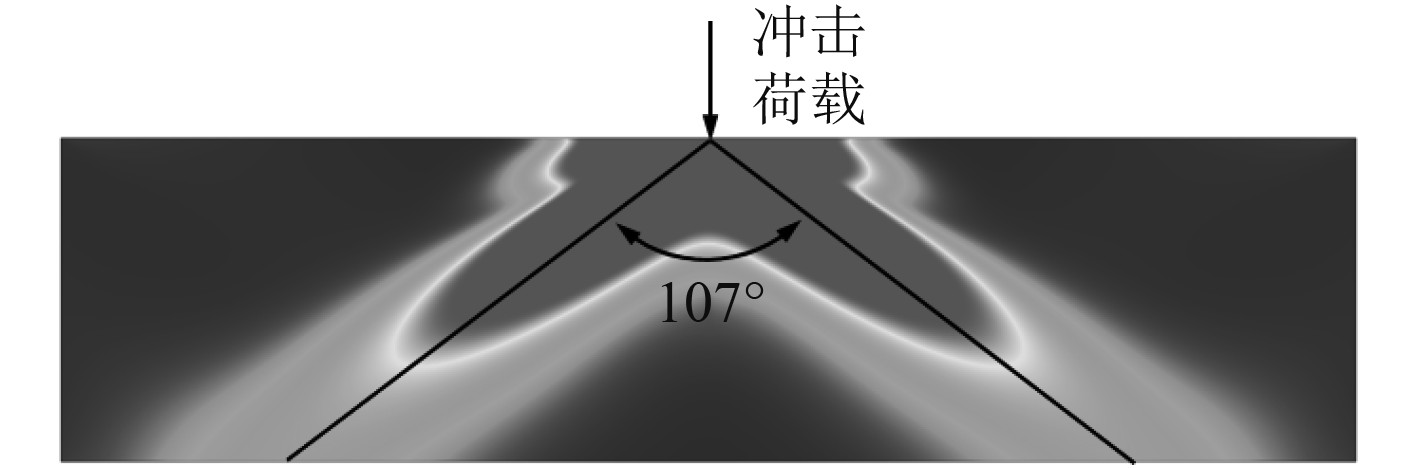
基于复杂微结构材料数值均质化方法,在COMSOL软件中,将微结构材料等效成均质材料,建立一矩形模型,边界设置为低反射边界。对矩形模型施加一半正弦冲击荷载,对该荷载进行频谱分析,其主要频率分布范围集中于5 000 Hz以下。输出材料中的机械能分布场,如图9所示。可以表明,机械能流具有一个明显的分叉角
|
图 9 第13层胞元数值均质材料能流特性 Fig. 9 Energy flow characteristics of homogeneous material with cell numerical value of the 13th layer |
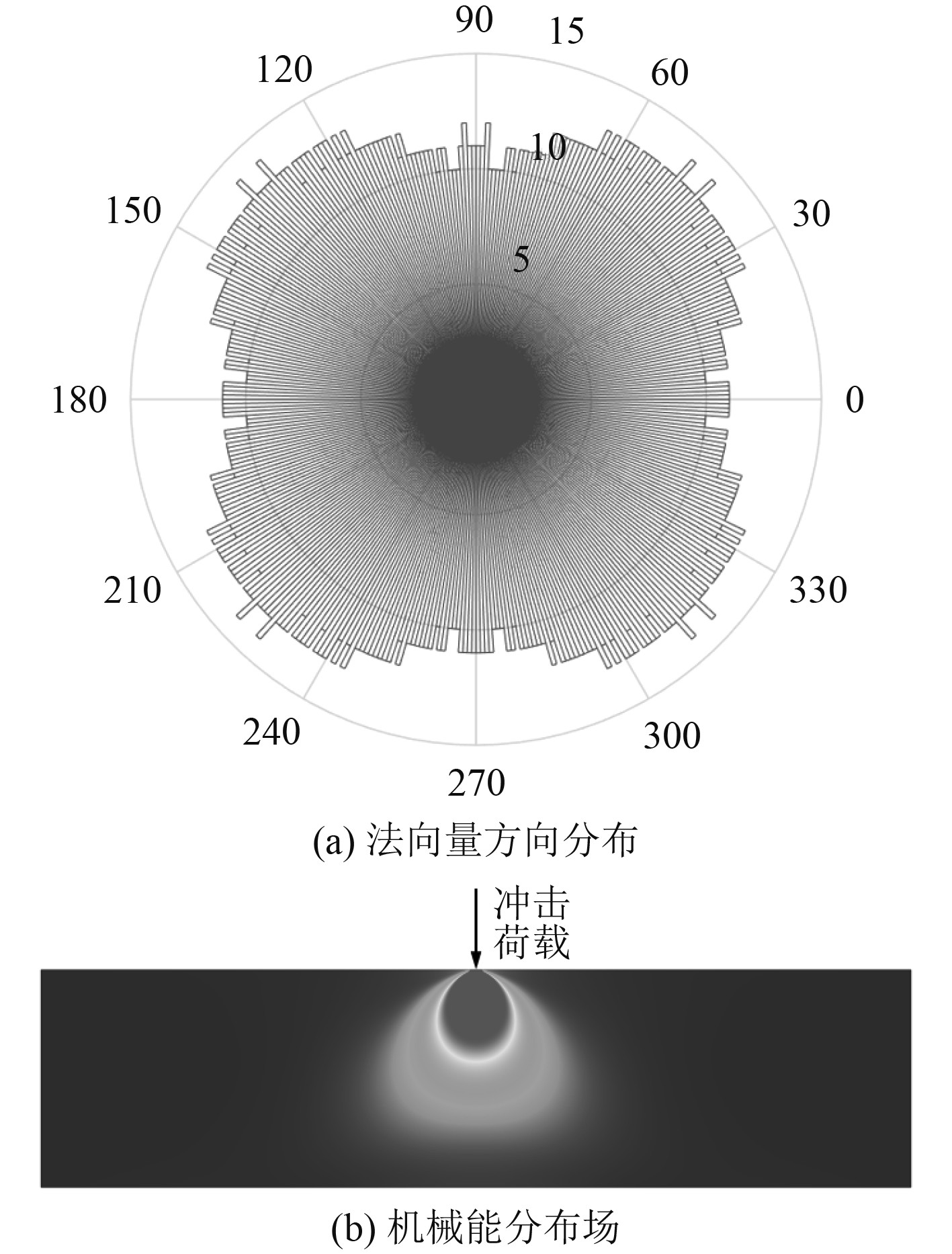
|
图 10 各向同性材料频散特性及能流特性 Fig. 10 Dispersion characteristics and energy flow characteristics of isotropic materials |
对比各层五模点阵胞元的法向量分叉角
基于13层胞元材料的能流分叉角

|
图 11 能流轨迹 Fig. 11 Energy flow trajectory |
胞元结构参数主要有斜杆长l、竖杆长h、拓补角β、壁厚t、配重半径r,现选取第13层胞元,通过单一改变某结构参数,获取该参数对能流分叉角

|
图 12
胞元结构参数对能流分叉角
|
本文基于坐标变换理论,设计制作了五模点阵环状结构试验模型,通过碰撞冲击试验、冲击仿真和频散特性分析等方法,揭示了碰撞冲击作用下五模点阵环状结构的动态响应,具体结论如下:
1)通过碰撞冲击试验发现,试验模型迎冲面与背冲面应变峰值之比ε1/ε3稳定在80%左右,与常规实心圆环有明显差异,说明试验模型对冲击应力波有明显的调控效果,可有效避免迎冲面结构率先发生破坏。
2)通过有限元仿真揭示了五模点阵环状结构受冲击的动态响应过程,仿真结果同试验结果的误差均在合理范围内。相较于等质量实心圆环,五模点阵环状结构迎冲面应变峰值降低了53%,背冲面应变峰值升高了18%。五模点阵环状结构ε1/ε3仅有86%,而等质量实心圆环高达220%,并且从应力分布来看,五模点阵环状结构中应力有一明显向两侧发散的趋势,可有效避免迎冲面的应力集中。
3)通过对胞元频散特性的分析,发现频散曲面等值线法向量的方向分布可以准确地反映材料中的能流特性。五模点阵环状结构各层胞元的机械能流均有一明显的分叉角,这从能量的角度解释了试验模型对冲击应力波的调控作用。此外,通过各层材料能流特性可以预测环状结构中的能流轨迹,进而对五模点阵环状结构进行局部加强,避免发生局部破坏。
4)通过研究胞元结构参数对能流分叉角
| [1] |
MILTON G W, CHERKAEV A V. Which elasticity tensors are realizable?[J]. Journal of Engineering, Materials and Technology, 1995, 117: 483-493. DOI:10.1115/1.2804743 |
| [2] |
MILTON G W, BRIANE M, WILLIS J R. On cloaking for elasticity and physical equations with a transformation invariant form[J]. New Journal of Physics, 2006, 8(10): 248. DOI:10.1088/1367-2630/8/10/248 |
| [3] |
NORRIS A N. Acoustic cloaking theory[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2008, 464(2097): 2411-2434. DOI:10.1098/rspa.2008.0076 |
| [4] |
SCANDRETT C L, BOISVERT J E, HOWARTH T R. Acoustic cloaking using layered pentamode materials[J]. Journal of the Acoustical Society of America, 2010, 127(5): 2856. DOI:10.1121/1.3365248 |
| [5] |
SCANDRETT C L, BOISVERT J E, HOWARTH T R. Broadband optimization of a pentamode-layered spherical acoustic waveguide[J]. Wave Motion, 2011, 48(6): 505-514. DOI:10.1016/j.wavemoti.2011.02.007 |
| [6] |
ARAVANTINOS-ZAFIRIS N, SIGALAS M M, ECONOMOU E N. Elastodynamic behavior of the three dimensional layer-by-layer metamaterial structure[J]. Journal of Applied Physics, 2014, 116(13).
|
| [7] |
LAYMAN C N, NAIFY C J, MARTIN T P, et al. Highly anisotropic elements for acoustic pentamode applications[J]. Phys Rev Lett, 2013, 111(2): 024302. DOI:10.1103/PhysRevLett.111.024302 |
| [8] |
TIAN Y, WEI Q, CHENG Y, et al. Broadband manipulation of acoustic wavefronts by pentamode metasurface[J]. Applied Physics Letters, 2015, 107(22): 221906. DOI:10.1063/1.4936762 |
| [9] |
CHEN Y, LIU X, HU G. Latticed pentamode acoustic cloak[J]. SciENTIFIC RepORTS, 2015, 5: 15745. DOI:10.1038/srep15745 |
| [10] |
LI Q, VIPPERMAN J S. Three-dimensional pentamode acoustic metamaterials with hexagonal unit cells[J]. The Journal of the Acoustical Society of America, 2019, 145(3): 1372-1377. DOI:10.1121/1.5093622 |
| [11] |
褚佳伟. 基于五模超材料的力学隐身斗篷结构设计[D]. 成都: 电子科技大学, 2019.
|
| [12] |
AMENDOLA A, BENZONI G, FRATERNALIi F. Non-linear elastic response of layered structures, alternating pentamode lattices and confinement plates[J]. Composites Part B:Engineering, 2017, 115: 117-123. DOI:10.1016/j.compositesb.2016.10.027 |
| [13] |
AMENDOLA A, CARPENTICES G, FEO L, et al. Bending dominated response of layered mechanical metamaterials alternating pentamode lattices and confinement plates[J]. Composite Structures, 2016, 157: 71-77. DOI:10.1016/j.compstruct.2016.07.031 |
| [14] |
AMENDOLA A, SMITH C J, GOODALL R, et al. Experimental response of additively manufactured metallic pentamode materials confined between stiffening plates[J]. Composite Structures, 2016, 142: 254-262. DOI:10.1016/j.compstruct.2016.01.091 |
| [15] |
LYMPEROPOULOS P N, THEOTOKOGLOU E E. Computational analysis of pentamode metamaterials for antiseismic design[J]. Procedia Structural Integrity, 2020, 26: 263-268. DOI:10.1016/j.prostr.2020.06.033 |
| [16] |
魏培君. 弹性波理论[M]. 北京: 科学出版社, 2021: 27−39.
|
 2023, Vol. 45
2023, Vol. 45
