0 引　言

极限强度是评价船舶结构承载能力的重要指标。近年来，学界对极限强度进行了广泛研究，并开发了一些有效方法，包括非线性有限元法^[1]、Smith法^[2]、理想结构单元法^[3]等。这些方法大多为准静态方法。

船体内底板承受面内载荷。Teixeira等^[4]研究了承受纵向压缩和侧向压力板的极限强度。Paik等^[5-6]研究了在组合双轴压缩和侧向压力作用下的板和加筋板的数值计算方法，并给出了一些指导性意见。Tanaka等^[7]研究了在纵向压缩作用下的加筋板，并通过与FEM结果进行比较，评估了一些用于预测极限强度的公式。

上述研究通过试验、解析及数值方法对船舶结构在各种载荷类型下的极限强度进行了广泛研究，并开发了许多实用的方法。但上述研究中考虑的载荷通常是静态的，并没有考虑动态影响。船舶经常在航行过程中承受动载荷，当船舶遭遇恶劣海况时，动载荷幅值可能会超过静载荷的几倍。船舶制造工艺的发展使船舶尺寸和航行速度不断增加，从而导致更高的波浪遭遇频率和更大的动载荷幅值。因此，有必要对船舶结构动力极限强度进行研究。

Cheong等^[8]通过试验研究了矩形板在面内流固冲击作用下的动态后屈曲特性，定义了动态塑性崩溃准则来估算板的承载能力，并讨论了边界条件和加载顺序的影响。Paik等^[9]对方形板在具有不同加载速度的单轴面内压缩载荷下的动态极限强度进行了一系列试验。Yang等^[10,11]研究了弹性约束矩形板在面内冲击作用下的动态屈曲，探究了扭转约束刚度，初始缺陷和脉冲持续时间的影响，并提出了新的动力屈曲准则。Yang等^[12]还通过非线性有限元方法研究了冲击弯矩作用下船体梁的动态极限强度。上述试验及数值研究表明，材料的应变率效应对动力极限强度的影响是显著的。因此，在研究船舶结构的动力极限强度时，必须考虑材料的非线性。

由于通过试验和数值方法研究动力极限强度都很费时，因此有必要建立经验公式来预测船舶结构的承载能力。Ao等^[13]研究了加筋板在纵向压缩载荷作用下的极限强度，并提出了一种新的改进公式来评估加筋板在面内单轴压力下的抗压极限强度。Yang等^[12]提出了一个经验公式用于预测面内动态压缩载荷作用下简支板的动力极限强度，并考虑了材料的非线性。

近年来，人工神经网络已被广泛应用于结构可靠性及强度预测等领域。在无加筋板、加筋板的强度预测方面，已被验证有比传统回归公式更好的计算精度^[15]。因此，本文考虑材料的非线性，在有限元分析的基础上，基于BP神经网络建立了加筋板动力极限强度的预测模型，并通过比较对实船结构神经网络的预测值和有限元结果，证明了该方法的精确性。

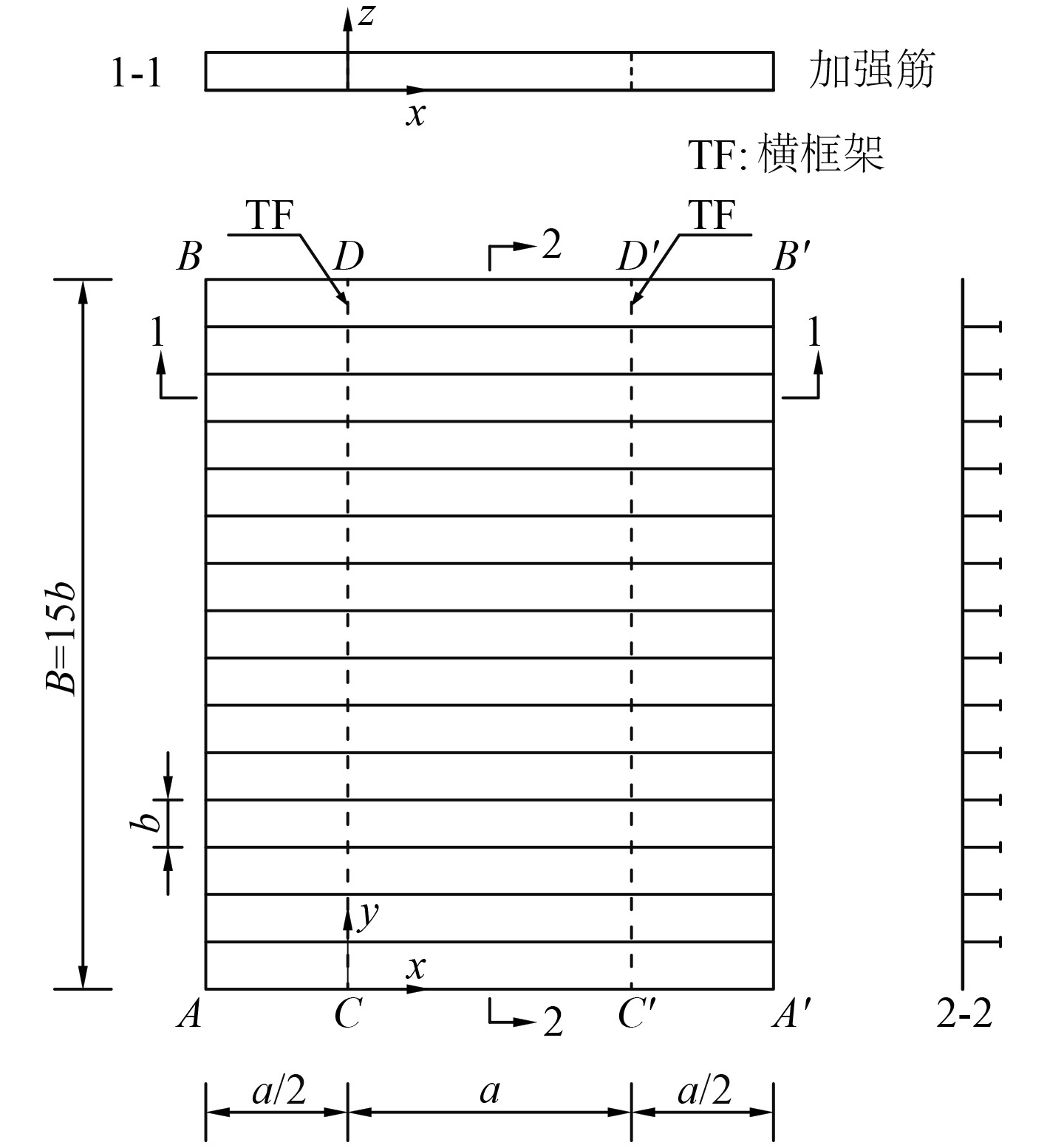
1 数值计算方法 1.1 模型几何、材料参数

加筋板几何参数如图1所示。x、y、z方向分别为纵向、横向与垂向。板长、板宽、加筋间距和带板厚度分别为a、B、b和 t_p。加强筋（含带板）剖面图如图2所示。加筋腹板高度、腹板厚度、翼板宽度、翼板厚度分别为t_w、h_w、t_f和b_f。 $\beta{=}{b}{/}{\text{t}}_{{p}}\cdot\sqrt{{\text{σ}}_{{Y}}\text{/}{E}}$ 为板格柔度系数； ${ \lambda }\text{=}{a}\text{/}\text{π}\cdot\sqrt{{A}\text{/}{I}}\cdot\sqrt{{\text{σ}}_{{Y}}\text{/}{E}}$ 为加筋梁柱柔度系数；A 为加筋含带板面积；I 为加筋含带板对带板中面惯性矩。

加筋板材料参数为杨氏模量E=2.06×10⁵ MPa；泊松比υ=0.3；密度ρ=7.8×10⁻⁹ t/mm³。材料屈服强度σ_y取值范围为 315～470 MPa。在动力极限强度计算中，需考虑材料的应变率强化效应。本文中，材料动力屈服应力以Cowper-Symonds公式给出:

$ {\sigma _{yd}} = {\sigma _y}\left(1 + {\left(\frac{{\overline \varepsilon }}{D}\right)^{1/q}}\right)。$

(1)

式中：σ_yd为动力屈服强度； ${\bar{ \varepsilon }}$ 为塑性应变率，D和q为材料常数，对高强度钢取D=3200 s⁻¹，q=5^[17]。

1.2 初始缺陷

在加筋板的制造过程中，必然产生一定程度的初始变形。而这些初始变形对加筋板的极限强度有显著的影响。因此，考虑板局部变形、梁柱形变形与加强筋侧倾变形3种形式的初始缺陷。

板局部变形模式为：

$ {w_p} = {\delta _0}\sin \left(\frac{{m {\text{π}} x}}{a}\right)\sin \left(\frac{{n {\text{π}} y}}{b}\right)。$

(2)

式中：n为板格局部变形横向半波数，一般取1；m为板格纵向变形半波数，一般取为满足式（3）的最小整数。

$ a/b \leqslant \sqrt {m(m + 1)} 。$

(3)

Smith通过统计实船船体板的变形，对加筋板初始变形幅值总结，以得出下规律：

$ {\delta }_{0}=\left\{\begin{array}{ll}0.025{\beta }^{2}{t}_{p}\text{，}&轻微缺陷；\\ 0.1{\beta }^{2}{t}_{p}\text{，}&平均缺陷；\\ 0.3{\beta }^{2}{t}_{p}\text{，}&严重缺陷。\end{array} \right.$

(4)

在计算中采用平均程度的初始缺陷幅值，以更好地反映实船板动力极限强度。

梁柱形变形模式如下式：

$ {w_s} = 0.0015a \cdot \sin \left(\frac{{{\text{π}} x}}{a}\right)\sin \left(\frac{{{\text{π}} y}}{b}\right)。$

(5)

加强筋侧倾变形模式如下式：

$ {\upsilon _s} = \frac{{0.0015a}}{{{h_w}}} \cdot z \cdot \sin \left(\frac{{{\text{π}} x}}{a}\right) 。$

(6)

1.3 边界条件与载荷

实船船体加筋板的四周均由强构件支撑，因此其边界条件介于简支与固支之间。在数值计算中，通常采用简支边界条件。本文所采用边界条件如表1所示。

所施加的动力载荷与Paik等^[9]的试验中所采用的载荷相同，如图3所示。为匀速位移加载，加载速度在整个加载过程中保持不变。

1.4 有限元模型

数值计算使用Abaqus软件，所采用的有限元模型如图4所示。模型全部采用S4R单元建立。在加筋间的板格宽度上划分10个单元，在腹板高度上划分6个单元，在翼板宽度上划分4个单元。加筋板两端剖面上的节点的x方向自由度被耦合在参考点上，位移载荷通过参考点施加。

1.5 计算模型

选用的加筋板主要形状参数为板柔度系数β及加筋梁柱柔度系数λ。根据Zhang等^[18]的研究结果，船体加筋板的β一般为1～2.5，λ一般为0.25～0.95。选用9个1～2.8的β值，加强筋的几何尺寸固定，其对应的λ为0.36～0.67。同时，为了反映材料屈服强度的影响，选用屈服强度分别为315 MPa、360 MPa、410 MPa及470 MPa4种的钢材。所有钢材均为高强度钢且广泛应用于船体结构制造。所有板的长度a=3 000 mm，加筋间距b=500 mm，加筋尺寸t_w=10 mm、h_w=200 mm、t_f=20 mm、b_f=60 mm。其余参数如表2所示。加载速度从0 s⁻¹到2.2 s⁻¹，每隔0.1取一个，共23种加载速度。

1.6 计算方法验证

本文主要讨论加筋板动力极限强度，因此使用Paik等^[9]的试验结果对计算方法进行验证。其对4块同样的四边简支方形板在不同速度载荷下的极限强度进行了试验。加载速度以平均应变率的形式表示，与加载速度的关系为：

$ \overline \varepsilon = \frac{{{V_0}}}{a}。$

(7)

式中：a为方形板的边长。加载速度V₀从0.05 mm/s增加到400 mm/s，对应的平均应变率为10⁻⁴ s⁻¹到0.8 s⁻¹。本文数值计算结果与试验结果对比如表3所示。可看出，本文结果与试验吻合较好，因此本文的计算流程能够用于计算加筋板在面内动态压缩作用下的极限强度。

2 BP神经网络

BP神经网络（Back-Propagation Network），又称反向传播神经网络，是一种应用较为广泛的神经网络模型，具有高度非线性和较强的泛化能力。BP神经网络包括：输入层、隐藏层和输出层，每一层都含有数个神经元。在训练过程中，神经元的激活值将从输入层经过隐藏层传向输出层，输出层的神经元输出对应于输入层神经元的响应。而后，通过比较输出层的输出值与真实值间的误差，通过误差逆向传播算法从输出层到输入层调节各神经元的权值与偏置，最小化输出的预测值与希望得到的预测值间的误差，从而使最终稳定的神经网络具有较高的预测精度。

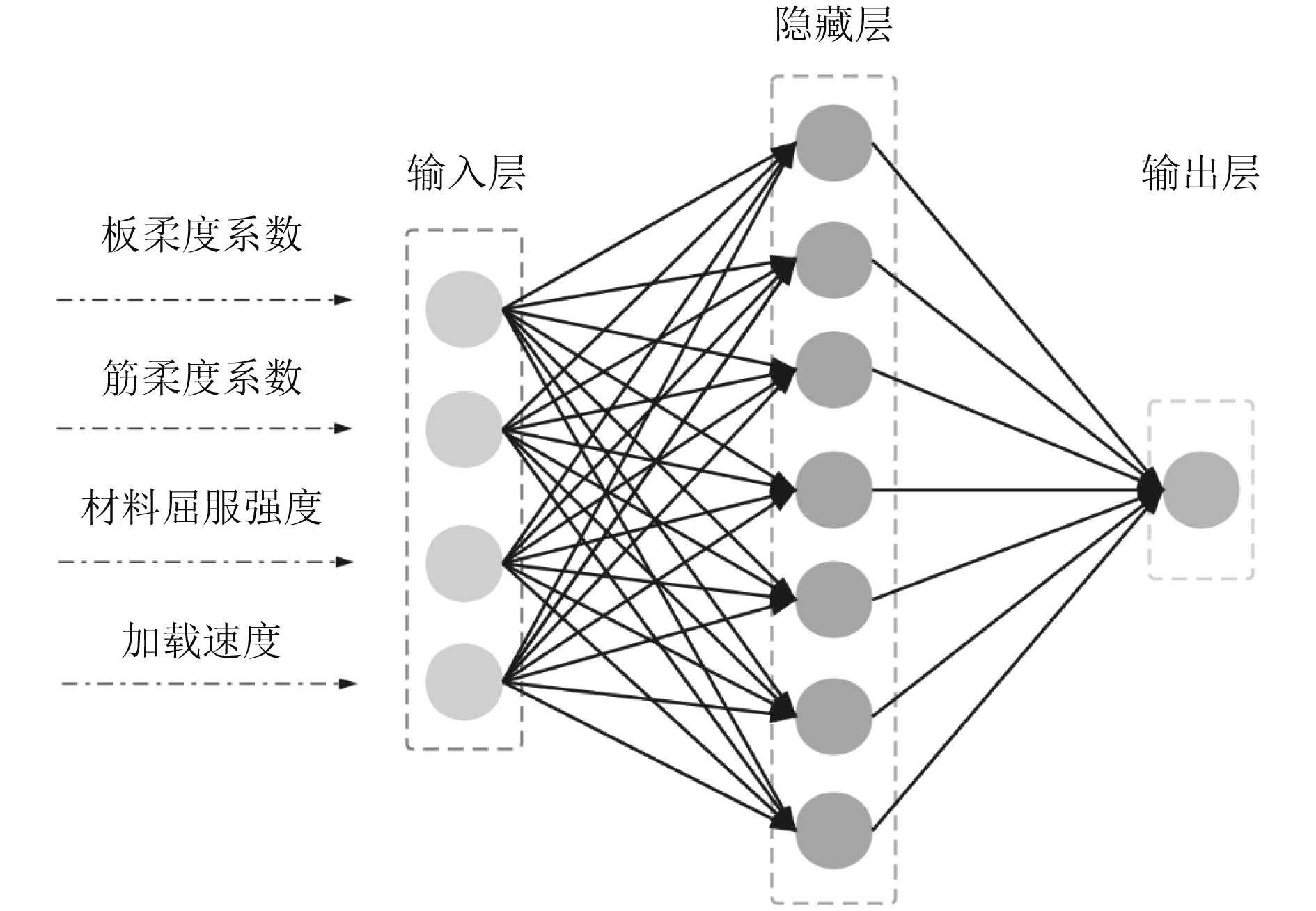
本文所采用的神经网络结构如图5所示。输入层由4个神经元组成，分别代表板柔度系数β、加筋梁柱柔度系数λ、材料屈服强度σ_y以及加载平均应变率 $\stackrel{\mathrm{-}}{{ \varepsilon }}$ 。通过多次试算调整，本文确定使用一层隐藏层，共7个神经元。输出层为一个神经元，表示动力极限强度与材料屈服强度之比σ_ud/σ_y。各层间通过权值w与偏置b连接，同一层间的神经元无连接。

隐藏层的传递函数采用Logsig函数，如下式：

$ f(x) = \frac{1}{{1 + \exp ( - x)}}。$

(8)

隐藏层中第j个神经元的输入为：

$ {y_j} = \left[ {\sum\limits_{i = 1}^m {{w_{ij}}{x_i}} } \right] + {b_j}。$

(9)

其中： $ {w_{ij}} $ 为输入层第i个神经元与隐藏层第j个神经元之间的权重； $ {b_j} $ 为隐藏层第j个神经元的偏置；m为输入层神经元的个数； $ {x_i} $ 为第i个输入神经元的值。隐藏层中第j个神经元的输出为：

$ {u_j} = \frac{1}{{1 + \exp ( - {y_j})}} 。$

(10)

输出层传递函数选择Purelin函数，如下式：

$ f(x) = x 。$

(11)

输出层的输入值为：

$ {y_{in}} = \left[ {\sum\limits_{k = 1}^n {{w_k}{u_k}} } \right] + b 。$

(12)

式中： $ {w_k} $ 为隐藏层第k个神经元和输出层之间的权重， $ b $ 为输出层的偏置。n为隐藏层神经元的个数。输出层的输出为：

$ {y_{{\rm{out}}}}{\text{ = }}{y_{{\rm{in}}}}。$

(13)

为评估BP神经网络的精度，采用相关系数R对运算结果进行评估：

$ R = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^p {({y_{{\rm{pred}}}} - {y_{{\rm{train}}}})} }}{{\displaystyle\sum\limits_{i = 1}^p {({y_{{\rm{pred}}}} - {{\overline y }_{{\rm{train}}}})} }}。$

(14)

其中：p为数据个数； ${y_{{\rm{pred}}}}$ 为输出的预测值； ${y_{{\rm{train}}}}$ 为输入的真实值。相关系数R表征预测值与真实值的相关程度，越接近1表示预测的准确性越高。

将所有样本分成训练集、验证集、测试集，各个集合的选取相互独立，分别占总样本的70%、10%、20%。其中，训练集用于对模型参数的训练，验证集用于对训练好的模型进行检验，评估其对训练集外数据的泛化能力，并反馈到训练过程中，对模型的超参数进行调整。在训练达到预期的误差精度后，网络训练完成。此时使用测试集检验最终模型的预测准确率。

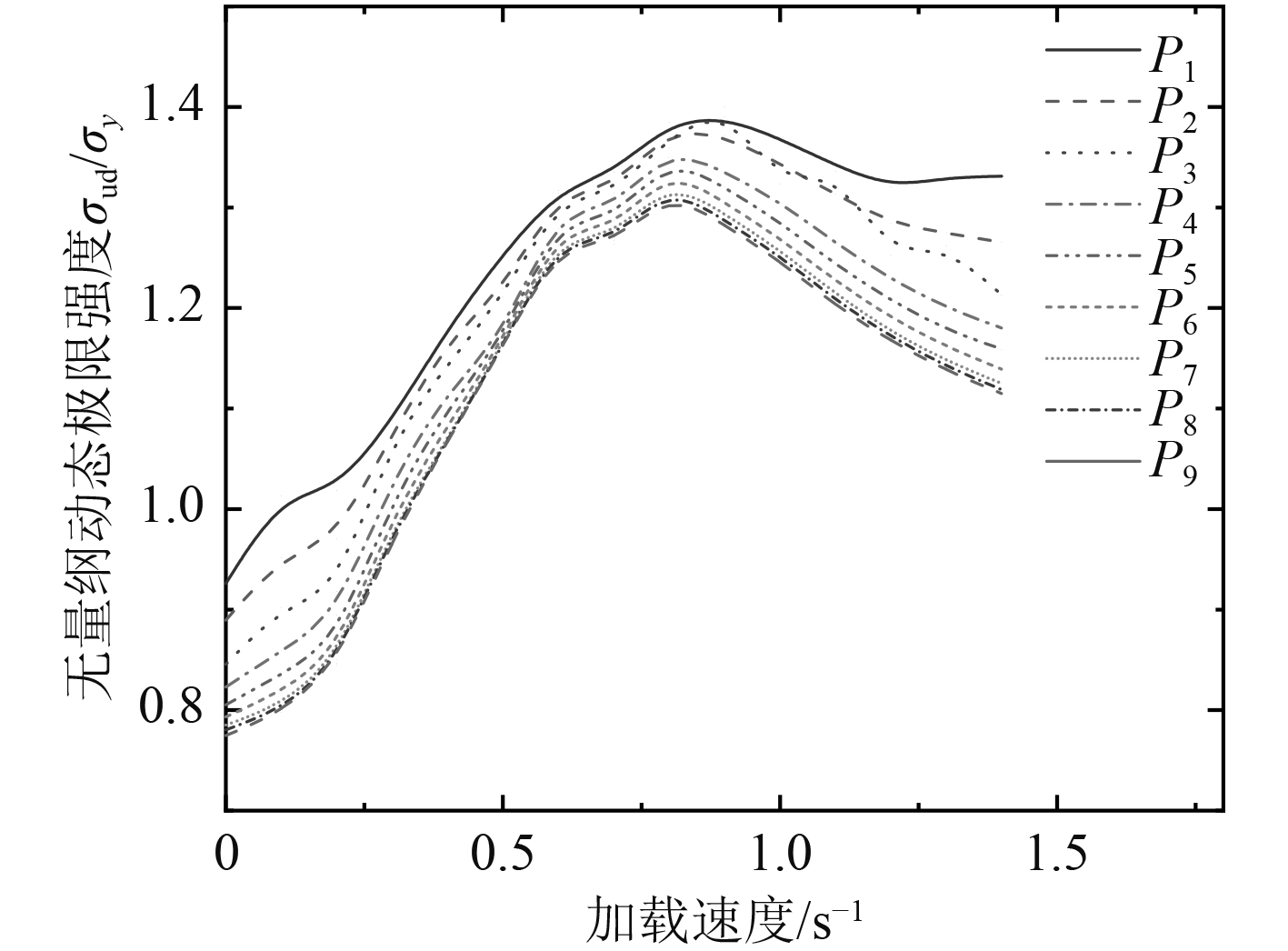
3 结果与讨论 3.1 加筋板动力极限强度数值结果

通过计算，共得到36×23=828组数据，如表4所示。由于数据量过多，仅展示部分。极限强度取值为计算所得载荷-端缩曲线的最高点，无量纲动态极限强度定义为结构极限强度与材料屈服强度的比值σ_ud/σ_y。图6为若干典型加筋板的动态极限强度随加载速度变化的曲线。分析发现，随加载速度提高，加筋板动态极限强度较静态情况下有显著的提高。这是由于在较高的加载速度下，材料应变率强化效应明显，材料的动态屈服强度较静态明显提高，且在高速载荷作用下，加筋板的高阶模态被激发，也使其极限承载力有所提高。

3.2 BP神经网络训练结果

采用4-7-1的3层BP神经网络结构，使用具有不同几何尺寸、不同材料属性的加筋板在不同加载速度下的动力极限强度数据对网络进行训练。由于各个输入参数的取值范围与波动存在明显差异，为保证训练精度，对样本参数进行归一化处理，使其均在[0,1]的区间内：

$ {x_i}' = \frac{{{x_i} - \min (S)}}{{\max (S) - \min (S)}},{x_i} \in S。$

(15)

即对于集合S内的任意元素，将其映射为其与集合内最小元素的差除以集合元素极差。对于BP神经网络的各项输入参数均进行此归一化处理，即可消除输入参数数值差异的影响。

训练结果如图7所示。图对角线y=x代表预测值与实际值完全相同。数据点分布越靠近该对角线，说明预测精度越高。从图中可看出，所有数据均落在对角线附近，相关系数R>0.99，说明在所有样本集上，网络的预测结果均与实际值有较高的吻合性。

基于该BP神经网络训练结果，可构建加筋板动力极限强度预测模型：

$ \begin{gathered} \frac{{{\sigma _{ud}}}}{{{\sigma _y}}} = \left[ {\sum\limits_{k = 1}^7 {{w_k}{u_k}} } \right] + b ，\\ {u_k} = \frac{1}{{1 + \exp ( - {y_k})}} ，\\ {y_k} = \left[ {\sum\limits_{i = 1}^4 {{w_{ik}}{x_i}} } \right] + {b_k}。\\ \end{gathered} $

(16)

式中，各参数值如表5及表6所示。

3.3 实船预测精度检验

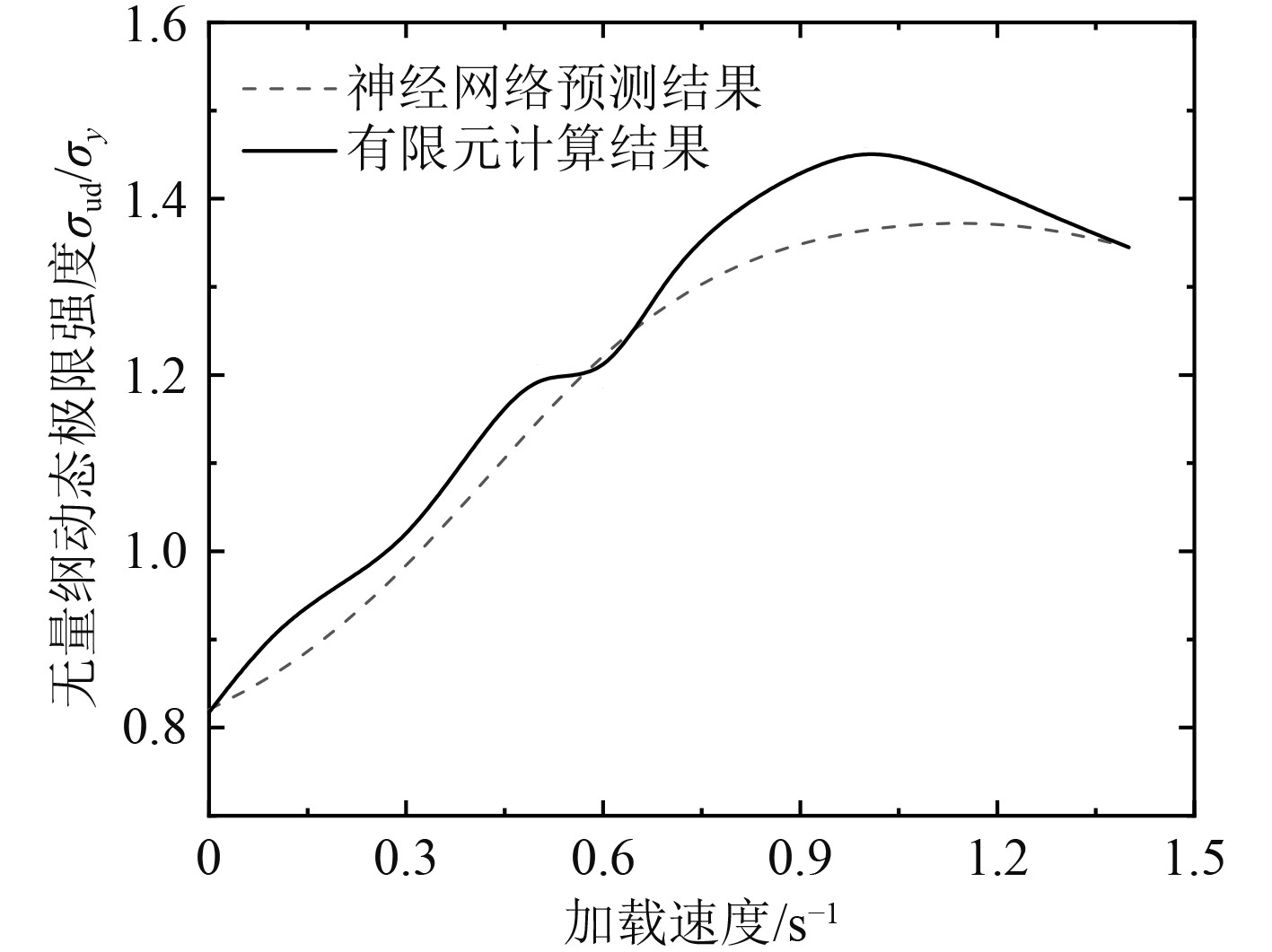
为检验该模型对实船加筋板的预测精度，选取10 000TEU集装箱船船底加筋板，对其动力极限强度进行预测。该加筋板的参数如表7所示。对其在0～1.4 s⁻¹下的动力极限强度进行预测，得到的结果如表8及图8所示。可看出，神经网络预测值与有限元结果较为接近，最大误差−6.4%，平均误差−3.1%。说明该模型能够较好地预测船体加筋板的动力极限强度。

4 结　语

船体结构动力极限强度是衡量其动力承载力的重要指标，但目前缺少对其进行快速计算的方法。本文通过Abaqus软件对828组船体加筋板动力极限强度进行计算，并基于BP神经网络建立了船体加筋板动力极限强度快速预测方法，得到以下结论：

1）通过大量的有限元计算，可以发现在较高加载速度下，加筋板的动态极限强度较静态有明显提高。这是材料的应变率强化效应及高速载荷激发了结构高阶变形模态的共同结果。

2）与非线性有限元的计算结果相比，BP神经网络预测的神经网络均方差与相关系数分别为0.00047与0.99，样本误差集中在−5%～5%区间内，具有良好的预测精度

3）依据设计的BP神经网络给出了船体加筋板动力极限强度快速预测方法，可为船体加筋板动力极限强度评估与设计提供参考。