2. 镇江市高等专科学校 电气与信息学院,江苏 镇江 212028
2. School of Electrical and Information, Zhenjiang College, Zhenjiang 212028, China
大型运输船舶的安全航行问题,一直以来都是航运界关注的重点问题之一。特别是近年来随着世界范围内经济发展形势的不断变化,许多国家都把海洋交通运输系统的安全性要求提到了新的高度,从而使得这个问题更加突出。因此,为确保大型运输船舶及海上设施的运行安全,颁布了载重线公约、SOLAS公约,并对海上运输的重大安全事故处理过程进行规范[1–3]。
在风浪水域中,海面波涛汹涌,风力和浪高都比较大,这将使得船舶受到强大的冲击力,从而发生滚动和倾斜。尤其是当风浪方向与船舶行驶方向垂直时,船舶更容易受到侧向的力量,导致侧倾或倾覆。在强风浪的环境下,船舶行驶速度通常会很慢,这是因为船舶需要克服风浪产生的阻力。而减缓航速可能会影响航行计划,并增加航行时间。长时间在风浪水域中航行,将会对船舶的结构产生大量振动和冲击,从而导致部分设备、管道和结构零件受损。同时,这些振动和冲击也可能引起带电设备的故障。因此,海上航行时必须谨慎处理风浪环境,并根据气象预报和海况变化做出相应的决策,例如调整航向和速度、加强监控和保养、采取防护措施等,以确保船舶和船员安全[4–5]。
本文提出的大型船舶自校正控制系统,能够基于船舶航行的相关参数对其直线航迹进行调整。以仿真形式对其展开研究,在论述其可行性后,提出相关大型船舶操纵建议,进一步丰富及完善大型船舶直线航迹相关研究。
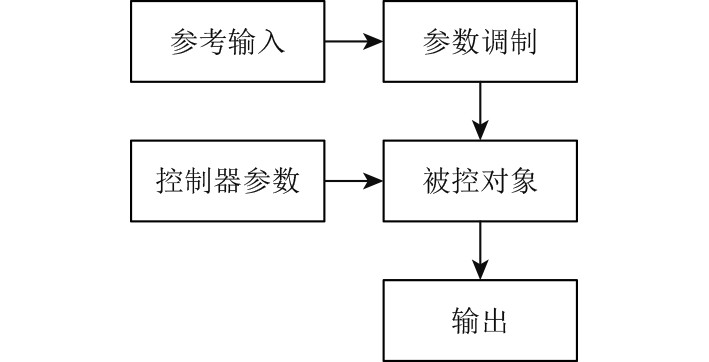
1 大型船舶自校正控制系统工作原理大型船舶自校正控制系统,主要是由自动优化控制系统结合自适应控制法(MRAS)而形成的一种应用型控制系统。大型船舶自校正控制系统流程如图1所示,该流程图描述了大型船舶自校正控制系统的参数控制过程。
|
图 1 大型船舶自校正控制系统工作流程 Fig. 1 Self tuning control system for large ships |
可知,该系统能够在确保稳定性的同时,对搜集到的信号进行针对性分析,最终实现将误差信号的出现几率降至最低。
2 大型船舶直线航迹自校正参数模型的确定 2.1 船舶参数选择以某大型船舶(VLCC)为例,利用数据采集与监视控制系统(SCADA)调取相关参数,设其载重量为20×104 t,长度为330 m,吃水为21 m。基于国际船舶与海洋标准(ISO11674),对该类型船舶的自身参数及航迹控制参数进行研究。
2.2 模型确定本文研究了大型船舶直线航迹自校正模型,并通过数学建模方法对参数模型进行分析,同时基于Lyapunov函数对非线性参数进行设计优化,其公式为:
| $ \left\{ {\begin{aligned} & {y = U\sin \psi },\\ &{\psi = r} ,\\ & {r = - \dfrac{1}{T}r - \dfrac{\alpha }{T}{r^3} + \dfrac{K}{T}\delta } 。\end{aligned}} \right. $ |
式中:y为大型船舶发生横向偏移,U为大型船舶航迹速度,
船舶首摇阻尼因风阻系数的降低而降低,同时由于VLCC的质量较大,该大型船舶从初速V0减至0后,其相对应的定速直线前进的航迹会更长。由此,假设某大型船舶排水量越大,其停船航程则越长,并且船舶减速过程中主机是根据计算机保护程序逐级降速的,在减速的初始阶段降速很明显,但是速度越小减速越慢,船舶载重和自重太大会导致惯性力矩太大,这就导致了低速阶段减速所需距离相对会比较大,船舶在满载时停船冲程更大。所以大型船舶直线航迹过程中,普遍存在推力中心偏位的问题。因此,需要加强大型船舶直线航迹的方向控制能力。设其控制律δ如下:
| $ \delta = \frac{K}{T}\left[ { - {k_1}k\left( {\psi + f\left( y \right)} \right) - \left( {{k_1} + k - \frac{1}{T}} \right)r + \frac{\alpha }{K}{r^3}} \right] 。$ |
以上模型与基于Lyapunov函数进行的非线性模型相同,在围绕大型船舶直线航迹自校正算法的基础上,考虑到大型船舶在航行中受航速、装载量以及水环境等因素的影响,其直线航迹将不会只受到船舶自身动力系统的影响,因此为保证大型船舶直线航迹自校正算法的准确性,进一步对其航迹控制律进行优化,继而得出最终的δ表达式:
| $ \delta=-k_{\psi}\left(\arctan\left(k_yy\right)+\psi\right)-k_rr-k_ar^3\text{。} $ |
基于前文相关参数及计算公式,对某大型船舶3个月的航迹偏差角度进行数据统计,在航迹计算公式上充分考虑了该大型船舶近3年的工作海况环境,对偏航轨迹进行统计,固定时间段内大型船舶航迹偏差角度如图2所示。其结果表明偏差角度在输入参量为10−4~10−3区间达到最大。

|
图 2 固定时间段内大型船舶航迹偏差角度 Fig. 2 Deviation angle of large ship’s trajectory during a fixed time period |
利用一段时间的平均航迹统计数据来描述航迹扇区的船体位置,平均偏差角度越大,说明船体与中央的距离越远,其航迹对风力的影响也就越小。平均自校正计算式为:
| $ De{g_{avr}} = \left| {\frac{{\sum {_{i = 1}^NDe{g_i}} }}{N}} \right. 。$ |
式中:Degavr为航迹偏离平均值,Degi为航迹偏离值i的取样值,N为统计期间对首摇角度取样的数目。
对一段时间航迹偏移的标准差进行统计,以此来描述该大型船舶的航迹偏离程度,其标准差愈大,则表示船体与首摇角度的离散度愈大,航迹偏移角的最大值愈大,而航迹偏角越大,则更加不利于船舶的直线航行。标准转角偏差计算公式为:
| $ Deg_{std}=\sqrt{\frac{1}{N-1}\times \sum\nolimits_{i=1}^N(Deg_i-Deg_{avr})^2}。$ |
式中,Degstd为航迹偏离标准差。由此对其进行仿真测试,得出不同转角条件下的直线航迹情况如图3所示。

|
图 3 不同转角条件下的直线航迹情况 Fig. 3 Straight line trajectory under different turning conditions |
可知,航迹的转偏角越严重,船舶直线航迹发生偏离的情况就越严重,其预测结果与实测结果之间的误差也会随之拉大。根据该大型船舶提供的相关资料统计结果,可以得出用Degavr和Degstd来表示大型船舶的工作状况关系,其中Degavr评估设备的航迹精度。为保证船舶能够保持一个直线的航迹行驶,需要尽可能地减小其绝对值。
然后用Degstd评估该大型船舶单位内的航迹偏离情况,发现转角60°要优于转角90°,转角90°优于转角120°。由此说明Degstd的数值愈低,大型船舶的航迹愈好。
3.2 直线航迹自校正控制系统误差分析偏航误差是一种不能被报告的故障,它不能从设备的数据中得到,必须从能源的观点来进行分析。在计算航迹偏离后,该大型船舶的总动量方程为:
| $ {P_x} = 2\rho {A_d}{v^3}a\times \cos \alpha 。$ |
当大型船舶出现偏差时,大型船舶最大功率输出点出现偏差,即α=a时,其功率特性最好。找出大型船舶最大输出航迹,并对其偏离度进行测量,从而判断大型船舶有无偏航。
假设该大型船舶的直线航迹平面与海浪的夹角为a,那么在该直线航迹平面上的竖向分量为:
| $ v_x=v\cos\alpha\text{。} $ |
那么大型船舶直线航迹自校正控制系统的总能量密度Py为:
| $ {P_{{y}}} = {(1 - a)^2}{\cos ^3}\alpha \text{。} $ |
由于不同转角对大型船舶直线方向产生影响而导致偏离,其自校正控制系统的能量损耗也会随之变大,理论上,由于海浪影响而导致大型船舶偏离的能量损耗,其关系如表1所示。
|
|
表 1 海浪造成的能量损失对应关系 Tab.1 Correspondence of energy loss caused by waves |
基于Lyapunov函数利用大型船舶的SCADA系统,获得其历史运行数据,主要包括航迹偏差角、发电机有功功率、特定条件下某大型船舶航行中的年平均风速、近岸海浪速度等。选择最普遍的航迹偏移角区间(60°,90°),分别间隔30°,同时分成6个区间,最后代入相关能量损失计算中,得出大型船舶直线航迹自校正控制系统受海浪的影响大小。
同时采用比因斯法,根据功率曲线的计算方法,在不同的航迹偏离部分下,利用SCADA系统调度该大型船舶近3年相关海浪数据,求出各区间的平均海浪影响下的船舶航速vj和平均功率Pj。
| $ {v_j} = {\rm{|}}\frac{1}{l}\sum\nolimits_{k = 1}^l {{v_{j,k}}} ,$ |
| $ {P_j} = {\rm{|}}\frac{1}{l}\sum\nolimits_{k = 1}^l {{P_{j,k}}} 。$ |
其中:Pj,k为满足第j段海浪影响的第k个功率,而vj,k为满足第j段海浪影响需求的第k个航速。采用瑞利积累函数对概率分布进行统计。瑞利累积概率分布函数是建立在该大型船舶的中心高度为固定值的基础上,然后需要计算出平均海浪影响速度Vavr 。其瑞利函数的描述方程为:
| $ FF_i = \sum\limits_{i = k}^{\text{l}} {} \left[ {F\left( {{v_i}} \right) - F\left( {{v_{i - 1}}} \right)} \right]\times \frac{{{p_{i - 1}} + {p_i}}}{2} 。$ |
最后得出区间i的大型船舶的偏航量为:
| $ {P_i} = \frac{{F{F_i}}}{{F{F_{\max }}}} 。$ |
在此范围内,大型船舶的偏航力系数Pi可以用来表示大型船舶的偏航角。总体思想是,在不同的航迹偏差范围内,通过对电力系统在不同方向上的功率分布进行分析,来反映各区域大型船舶的航迹控制效果。
此外,通过对各区间的功率曲线的卷积,可以确定输出功率的特征参数,经过标准化处理后,得到各区间的出力系数,并得到最佳的航迹自校正控制系统参数。
4 大型船舶操纵应注意的事项大型船舶在海面行驶中,由于受到风浪的作用,其受力面积较大,进出港的时候要特别注意因此导致船只在航向上发生偏移的现象。作为操作人员在驾驶大型船舶的过程中,需要为其预留足够的空间以防受外部因素影响而导致船舶直线轨迹发生偏移,并减少伴随出现诸如搁浅、触礁等意外情况。
为有效提升大型船舶的出行安全,基于研究所得数据可知,当船舶从常速100 r/min下降到可以机动操纵速度83 r/min时,需要按照一定的保护程序逐步减速,大约需要20~30 min。若是在港口停泊时发生严重故障,或是遇到其他紧急情况,则可能会延误船期、增加成本甚至导致沉没损失。所以进港口停船舶前,要做好充足的准备。停泊前事先做好计划,查看主机的换向操作,再根据情况调节船速,到达预设的停船点。
5 结 语本文首先对大型船舶的航迹自校正控制系统的工作原理进行介绍,然后根据航迹系统的控制需求,结合自校正控制算法对系统的关键参数进行数学建模和分析,并通过仿真和测试比对了各个角度下自校正控制算法的效果。结果表明,该自校正控制算法误差较小,能够满足大型船舶的直线航迹控制要求。
| [1] |
郭林, 刘飞, 李佳钰, 等. 基于能量管理策略的太阳能无人机航迹跟踪控制[J]. 西北工业大学学报, 2023, 41(2): 409-418. GUO Lin, LIU Fei, LI Jia-yu, et al. Track tracking control of solar UAV based on energy management strategy[J]. Journal of Northwestern Polytechnical University, 2023, 41(2): 409-418. DOI:10.1051/jnwpu/20234120409 |
| [2] |
蔡佳澄, 束庆霏, 宋政, 等. 基于输电杆塔的无人机精细化巡检研究[J]. 电工技术, 2023(7): 104. CAI Jia-cheng, SHU Qing-fei, SONG Zheng, et al. Research on refined inspection of UAV based on transmission tower[J]. Electrical Technology, 2023(7): 104. DOI:10.19768/j.cnki.dgjs.2023.07.027 |
| [3] |
HU Jia-wei, JIA Ze-qun, SUN Yan-tao, et al. Analysis of multi-UAV collaborative mission planning problems under multiple constraints and review of solution methods[J]. Computer Science, 2023, 50(7): 176-193. |
| [4] |
刘艳, 李文波, 刘新彪, 等. 复杂环境下无人机三维航迹规划及避障算法[J]. 电光与控制, 2023, 30(5): 93. LIU Yan, LI Wen-bo, LIU Xin-biao, et al. Three-dimensional UAV track planning and obstacle avoidance algorithm in complex environment[J]. Electro-optic and Control, 2023, 30(5): 93. DOI:10.3969/j.issn.1671-637X.2023.05.018 |
| [5] |
黄立文, 刘进来, 贺益雄, 等. 狭窄弯曲航段自动航迹控制方法研究[J]. 武汉理工大学学报, 2023, 45(4): 53-62. HUANG Li-wen, LIU Jin-lai, HE Yi-xiong, et al. Research on automatic track control method for narrow and curved flight sections[J]. Journal of Wuhan University of Technology, 2023, 45(4): 53-62. |
 2023, Vol. 45
2023, Vol. 45
