0 引　言

船舶在不同海域航行时，受风浪、能见度等众多因素影响^[1]，采用固定航线航行时，容易由于环境因素影响船舶的航行安全^[2]。为了保障船舶顺利、安全到达目的地，需要制定科学、合理的航线，满足船舶的安全航行需求^[3]。如何获取船舶的最优航行路线，是海洋领域的研究重点。数据驱动指利用软件、网络等手段采集数据，以海量数据为基础，从中挖掘有用数据，利用数据挖掘结果驱动不同应用顺利进行的重要方法。数据驱动方法可以实现海量数据的统计、分析、评估与利用，为船舶航行优化等应用提供数据基础。利用数据驱动方法的数据分析、统计与评估结果^[4]，为海洋等不同领域应用提供优化策略。将数据驱动方法应用于船舶航线优化中，具有较强的现实意义。

目前已有众多学者针对船舶航线规划问题进行研究。黄佳佳等^[5]考虑化学品船舶航行的特殊性，设置了货舱禁止更换的约束条件，构建化学品船航线规划的线性规划模型，通过模型求解获取化学品船的航线规划结果。该方法满足带货舱船舶规划需求，令化学品船通过航线规划结果，获取最大利润。吴恭兴等^[6]对船舶航线规划时，充分考虑了气象变化对船舶航行的影响，设置气象参数作为船舶航行规划的路径代价函数，利用启发式函数获取规避风险的航线。该方法有效避开高风险的危险海域，实现船舶航线参数的有效规划。以上方法虽然可以有效规划船舶航线，但是存在运算过程过于复杂，影响船舶规划实时性的缺陷。针对以上方法在航线规划中存在的问题，研究基于数据驱动的航线实时优化方法。利用数据挖掘方法聚类处理影响船舶航行的相关数据，利用聚类结果驱动航线优化应用。采用数据驱动方法获取的航线优化结果，保障所生成的航线满足船舶航行的实际需求。

1 船舶航线实时优化 1.1 船舶航线优化总体结构

船舶航行前确定航线时，需要明确船舶航行区域海况。基于数据驱动的船舶航线实时优化流程如图1所示。

可以看出，利用数据驱动方法构建海况知识库。依据海况知识库内的海况信息与转向点，将船舶航线划分为不同航段，是航线优化的前提。利用海况知识库与转向点信息构建航线分段模型，将航线转向点信息、海况预报信息等信息输入分段模型中，识别船舶航行海况，将航线划分为不同的航段。确定船舶航行的航段后，输入航程、航行参数、航速等信息，利用航线实时优化模型，实现航线的实时优化。利用数据驱动方法定期更新航线的海况信息，根据海况信息更新结果实时优化船舶航线。

1.2 基于数据驱动的船舶航线海况数据库构建

利用海量的海况数据，构建船舶航线优化的海况知识库。提取船舶目标航线所在海域，船舶定航线航行的历史数据；利用天气预报中心下载航线所在海域的风速、风向、波高等数据^[7]；利用计程仪获取船舶航行的历史流速、流向等数据；利用GPS系统采集船舶的对地航速与航行矢量等数据。依据时间序列，整理所采集的船舶航行相关的海况数据，构建海况数据库。为了明确待优化船舶航线的海况类别，将所构建的船舶航线海况知识库，作为确定海况的训练样本。依据数据驱动方法，利用K-means聚类算法，对船舶航行海况数据聚类构建海况知识库。海况知识库的构建过程如下：

步骤1　从采集的海量海况数据中，随机选取 $ K $ 个海况数据，作为构建海况知识库的聚类中心c_i。

步骤2　计算聚类中心c_i与海况样本x_i之间的距离，确定与聚类中心距离最近的海况数据，将样本x_i与聚类中心c_i划分为相同类别。二者距离为：

$ d\left( {{x_i},{c_i}} \right) = \sqrt {\sum\limits_{j = 1}^n {{{\left| {{x_{ij}} - {c_{ij}}} \right|}^2}} } 。$

(1)

式中， $ j $ 表示海况样本x_i的特征属性。

步骤3　选取某海况类别中，全部海况样本的中心点，作为海况知识库聚类的新聚类中心，新聚类中心的表达式为：

$ {c'_i} = \sum\limits_{j = 1}^n {\frac{{{x_{ij}}}}{{\left| {{c_i}} \right|}}}。$

(2)

步骤4　重复以上过程，设置算法终止的收敛函数计算公式为：

$ E = \sum\limits_{i = 1}^k {\sum\limits_{x \in {c_i}} {{d^2}} } \left( {{c_i},x} \right) 。$

(3)

重复运算直至收敛函数和聚类中心固定时，结束聚类，否则转至步骤2继续计算。

通过以上过程，利用聚类结果构建海况知识库。根据海况知识库内的船舶航线信息与航线转向点信息，将船舶航线划分为不同航段。

1.3 构建船舶航线实时优化模型

依据船舶航线的航段划分结果，对不同航段的船舶航线进行实时优化。选取船舶航行的总时间最短以及总油耗最低，作为船舶航线实时优化模型的目标函数，船舶航线实时优化目标函数表达式为：

$ \min T = \sum\limits_{i = 1}^N {\left[ {\frac{{{d_i}}}{{{v_1}}} \times f\left( \xi \right)} \right]}，$

(4)

$ \min G = \sum\limits_{i = 1}^N {\left[ {\frac{{{d_i}}}{{24{v_1}}} \times g\left( {{v_2}} \right) \times f\left( \xi \right)} \right]} 。$

(5)

式中： $ G $ 与 $ T $ 分别表示船舶航行的总油耗以及总航行时间，g(v_i)与d_i分别表示船舶主机每日油耗以及第 $ i $ 段航线的距离，v₁与v₂分别表示第 $ i $ 段航线的对地航速以及对水航速， $ N $ 与f(ξ)分别表示船舶航线的航段总数以及惩罚函数。

船舶对水航速与对地航速间的关系表达式为：

$ {v_2} = {v_1} - \Delta {v_i} 。$

(6)

式中， $ \Delta {v_i} $ 表示船舶在航段 $ i $ 的航速损失。

船舶航行时，受海况影响，容易出现失速情况。受风浪波动影响，主机固定，航速较低时，航速变化为自然失速。船舶受风浪影响时，为了避免出现危险，需要有意减速。不同类型的航速变化，均可能导致船舶航行出现速度损失。船舶航行时的速度损失表达式为：

$ \Delta {v_i} = {v_2}\alpha \beta \delta /100。$

(7)

式中： $ \alpha $ 与 $ \beta $ 分别表示方向衰减系数与速度衰减系数， $ \delta $ 表示船舶型号。

船舶主机油耗的计算公式为：

$ g = av_2^3 + bv_2^2 + c{v_2} + d。$

(8)

式中， $ a $ 、 $ b $ 、 $ c $ 、 $ d $ 均为拟合系数。

为了使船舶航线实时优化过程更加符合船舶航行的实际海况，为航线实时优化模型设置如下约束条件：

1）船舶的实际航速 $ v $ ，需要低于船舶的额定航速(v_min,v_max)，该约束条件的表达式如下：

$ {v_{\min }} \leqslant v \leqslant {v_{\max }}。$

(9)

2）船舶航线优化的转向点位置，需要与船舶航线圆航段的固定距离 $ h $ 垂直，约束表达式为：

$ \Delta {d_i} \leqslant \frac{h}{2}。$

(10)

式中，△d_i表示船舶航线优化点 $ i $ 与基准点的间距。

1.4 船舶航线实时优化模型求解

选取蚁群优化算法求解所构建的船舶航线实时优化模型。蚁群算法利用信息素浓度变化，确定满足约束条件的最短路径，获取船舶航线实时优化的最优结果。 $ n $ 表示航线的转向点数量，τ_ij(t)表示时间为 $ t $ 时，航线转向点 $ i $ 与转向点 $ j $ 之间的信息素浓度， $ m $ 表示蚂蚁总数。 $ P_{ij}^k\left( t \right) $ 表示时间为 $ t $ 时，蚂蚁 $ k $ 从 $ i $ 移动至 $ j $ 的状态转移概率， $ P_{ij}^k\left( t \right) $ 的计算公式为：

$ {P}_{ij}^{k}\left(t\right)=\Bigg\{\begin{array}{l}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\varphi }\times {\left[{\eta }_{ij}\left(t\right)\right]}^{\phi }}{{\displaystyle \sum {\left[{\tau }_{ik}\left(t\right)\right]}^{\varphi }\times {\left[{\eta }_{ik}\left(t\right)\right]}^{\phi }}}\text{，}j\in allowed，\\ 0\text{，}{\rm{other}} 。\end{array} $

(11)

式中： $ \phi $ 与 $ \varphi $ 分别表示启发因子与期望因子， $ allowed $ 与 $ {\eta _{ik}}\left( t \right) $ 分别表示蚂蚁可选取的全部船舶航行转向点以及启发函数。

蚁群算法通过迭代确定最短搜索路径后，更新船舶航线转向点之间的信息素。信息素更新公式为：

$ {\tau _{ij}}\left( {t + n} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} \left( t \right)。$

(12)

式中， $ \Delta \tau _{ij}^k\left( t \right) $ 与 $ \rho $ 分别表示蚂蚁在 $ i $ 与 $ j $ 之间的信息素增量以及挥发系数。

利用该算法求解船舶航线实时优化模型时，无需更新全部蚂蚁对模型求解的信息素，仅需更新部分具有最优路径的蚂蚁信息素，保证了航线实时优化的运算效率。

2 性能测试与分析

为了验证所研究的船舶航线实时优化性能，选取某海域某船舶的某航线作为优化目标。待优化船舶航线的目标船舶的参数设置如表1所示。

本文方法选取数据驱动方法构建船舶航线的海况数据库。船舶航线在不同海况时，海况数据库聚类结果如表2所示。可以看出，采用本文方法通过数据驱动方法，获取船舶航线的海况数据。利用船舶航线的海况数据，将航线划分为不同的航段。

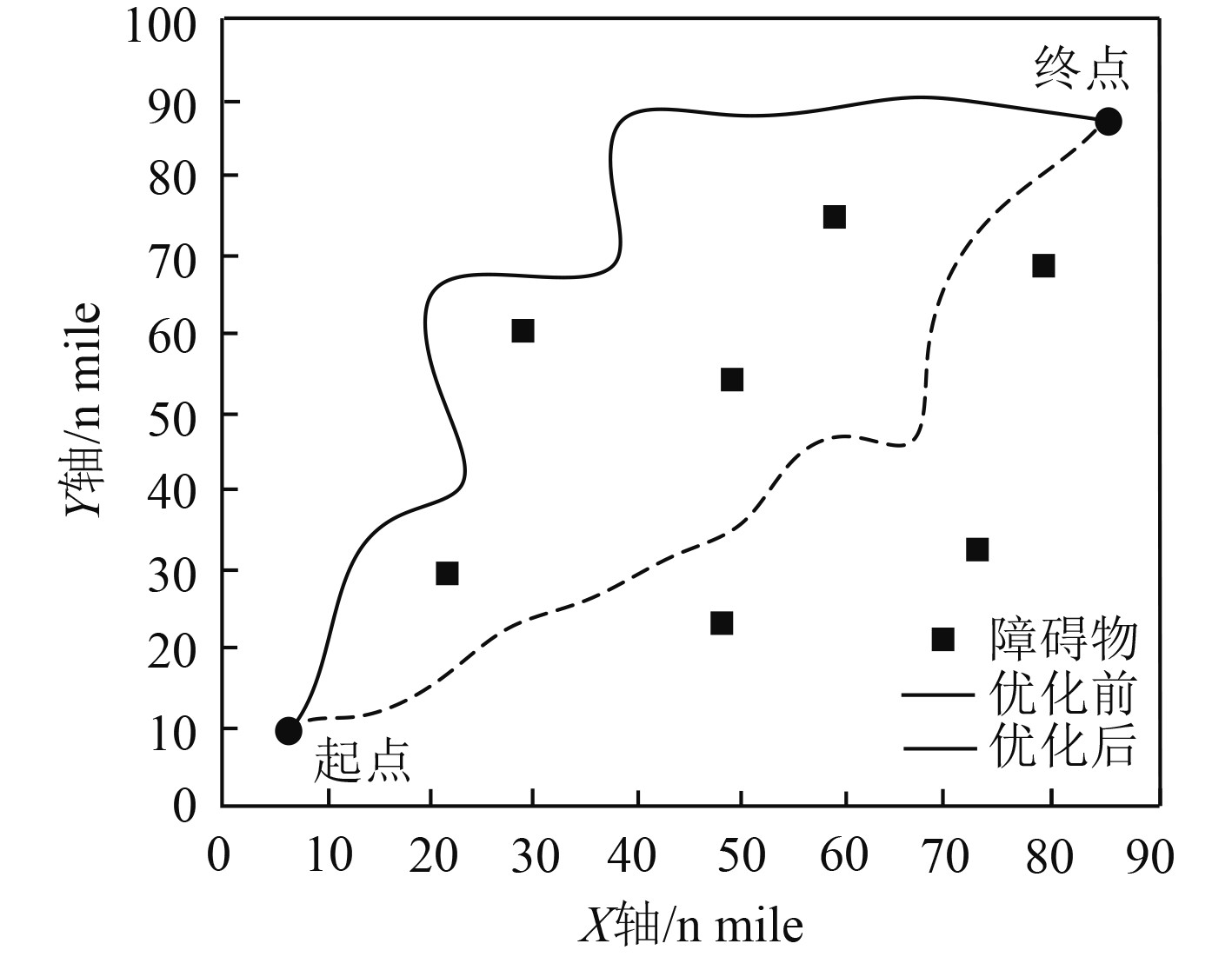
依据航线的航段划分结果，采用本文方法对船舶航线进行实时优化，优化结果如图2所示。可以看出，采用本文方法可以对船舶航线进行实时优化。本文方法考虑了不同海况对船舶航行的影响，令航线优化结果更加满足船舶航行的实际需求。

为了进一步衡量本文方法的船舶航线实时优化性能，统计采用本文方法对船舶航线进行实时优化，优化前与优化后船舶的航行时间以及船舶航行的主机总油耗变化，统计结果如图3和图4所示。可以看出，本文方法可以依据海况变化，对船舶航线进行实时优化。本文方法优化后的船舶航行时间与主机总油耗均低于优化前，验证本文方法的航线优化性能。图3和图4的实验结果，从船舶的航行总时间和主机总油耗2个方向，全面验证本文方法具有的航线优化性能，本文方法为船舶的可靠运行提供了良好的基础。

3 结　语

数据驱动方法是智能算法中的重要技术，利用数据驱动方法，确定影响船舶航线优化结果的海况数据。利用船舶海况数据聚类结果，构建船舶航行优化模型，获取科学、合理的、具有较高安全性的船舶航行路线。通过实验验证，采用该方法获取的船舶航行优化结果，船舶主机油耗低，降低了航行总时间，具有较高的实用性，适用于不同海况下的船舶航线优化。