磁异常场作为舰船、潜艇等目标的固有物理场,包含丰富的目标特征信息[1-2],但水上磁异常测量成本高、效率低,常采用航磁测量的方法测量水上及水下目标的磁异常。现有的磁异常数据延拓方法延拓深度有限,无法充分利用航磁测量数据。航磁测量具有施工效率高、成本低、探测范围大等诸多优点,其探测到的场值是由探测点位以下所有场源形成的叠加场,即每一个测点数据中都包含若干个场源的信息[3-4]。一般的航磁测量中只会测量获得某条测线或某个观测面内的数据,为节约探测时间成本,其他区域的磁异常数据只能依赖于对已知数据的空间转换。因而磁异常数据的空间转换在航磁测量中的作用非常重要,准确高效的磁场数据转换是资料处理中的重要环节,能够扩展数据内涵,突出目标,一定程度上减少探测结果的多解性,有效降低后续资料解释的难度,是航磁数据处理中的重要环节[5]。
磁法勘探中的位场数据空间转换方法包含向上延拓和向下延拓,向上延拓方法在数学上属于狄里希莱问题,是一个适定问题,具有唯一且稳定的解,在实际计算中只要保证参与计算的点足够多,便能够得到准确的结果[6]。但向下延拓是一个不适定问题[7-8],无法直接求解,国内外诸多学者针对这一问题提出了多种解决方法。早在20世纪40年代,Evjen[9]采用Taylor级数方法进行位场数据的解析延拓,其后Peters 利用该方法推导出向下延拓公式。1958年,Dean[10]利用傅里叶变换,首次将空间域中无法直接求解的向下延拓问题引入到频率域中,并推导出频率域中的延拓算子,但该方法仅能进行2倍点距的下延[11]。2002年,Fedi[12]提出了向下延拓的 ISVD(integrated second vertical derivative)法,该方法是指在进行 Taylar级数展开时,奇数阶和偶数阶垂向导数采用不同求解方法,奇数阶先求解垂向积分,再利用 Laplace 方程进行求解,而偶数阶直接利用Laplace方程求解,该方法能够稳定地进行5倍点距的下延。2006年,徐世浙[13-14]提出了积分迭代的位场延拓方法,该方法通过将不稳定的向下延拓问题转换为稳定的向上延拓问题,提高了延拓的最大深度,有效延拓深度可达20倍数据点距,该方法是目前最常用的位场数据延拓方法之一[15]。但多次迭代的方法影响计算速度,而迭代次数过少影响计算延拓精度,而且这一方法会在一定程度上放大噪声信号[16-17]。
本文提出一种基于BP神经网络的磁异常数据延拓方法,并构建由球体和长方体组成的混合模型。经模型试验验证,发现该方法延拓精度高,抗干扰能力强,能够有效解决向下延拓中计算不稳定的问题。
1 位场数据向下延拓数学模型位场数据向下延拓问题在数学上是一种不适定问题,作为现代地球物理学中最早利用数学原理解释资料的方法之一,国内外诸多学者曾对位场数据向下延拓原理做过深入全面的分析,向下延拓具有完善的数学理论基础。
位场的延拓问题实质上是求解式(1)中的柯西问题:
| $ \left\{ {\begin{aligned} & {\displaystyle\frac{{{\partial ^2}{u_h}}}{{\partial {z^2}}} + (\displaystyle\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}){u_h} = 0} {\text{,}}\\ & {u\left| {_{z = 0} = {u_0}(x,y)}。\right.} \end{aligned}} \right. $ | (1) |
式中:u0为已知的观测面场值,uh为空间内场源以上、观测面以下的位场场值。根据向上延拓公式,uh与u0具有如下关系:
| $ {u_0}(x,y) = \frac{1}{{2{\text{π}} }}\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\frac{{h{u_h}(\xi ,\eta )}}{{{{\left[ {{{\left( {x - \xi } \right)}^2} + {{(y - \eta )}^2} + {h^2}} \right]}^{3/2}}}}{\rm d}\xi {\rm d}\eta } }。$ | (2) |
根据式(2)向上延拓公式反求解uh的过程即为位场数据的向下延拓问题,因此,可将式(1)的柯西问题改写为:
| $ \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {\kappa (x,y){u_h}(\xi ,\eta ){\rm d}\xi {\rm d}\eta } } = {u_0}(x,y)。$ | (3) |
其中,
| $ \kappa (x,y) = \frac{h}{{2{\text π} {{({x^2} + {y^2} + {h^2})}^{3/2}}}}。$ | (4) |
式(3)积分可表示为褶积形式:
| $ \kappa (x,y) \otimes {u_h}(x,y) = {u_0}(x,y)。$ | (5) |
通过傅里叶变换可将时域中的褶积问题转换为频域中的乘积问题,因此,频域中的磁异常向下延拓问题可表示为:
| $ {U_h}(u,v) = {U_0}(u,v){\varPhi ^{ - 1}}(u,v){\text{。}} $ | (6) |
式中,
| $ \varPhi (u,v) = {e^{ - 2{\text π} h\sqrt {{u^2} + {v^2}} }}。$ | (7) |
采用快速傅里叶变换直接求解、积分迭代、奇异值分解等方法对其进行数值求解,在理论上可以进行10~20倍点距的向下延拓。但对于更多倍点距的延拓问题,或在信噪比较低的情况下,这类方法会出现延拓结果失真严重的问题。
2 基于BP神经网络的磁异常向下延拓方法BP神经网络是当前最为常用的多层前馈神经网络,具有强大的学习和纠错能力。当学习样本充足且准确时,对于复杂非线性问题能够将误差控制在足够小的范围内。BP神经网络包括输入层、隐含层和输出层3种结构,当问题较为复杂时,隐含层可以包含多层,其拓扑结构如图1所示。
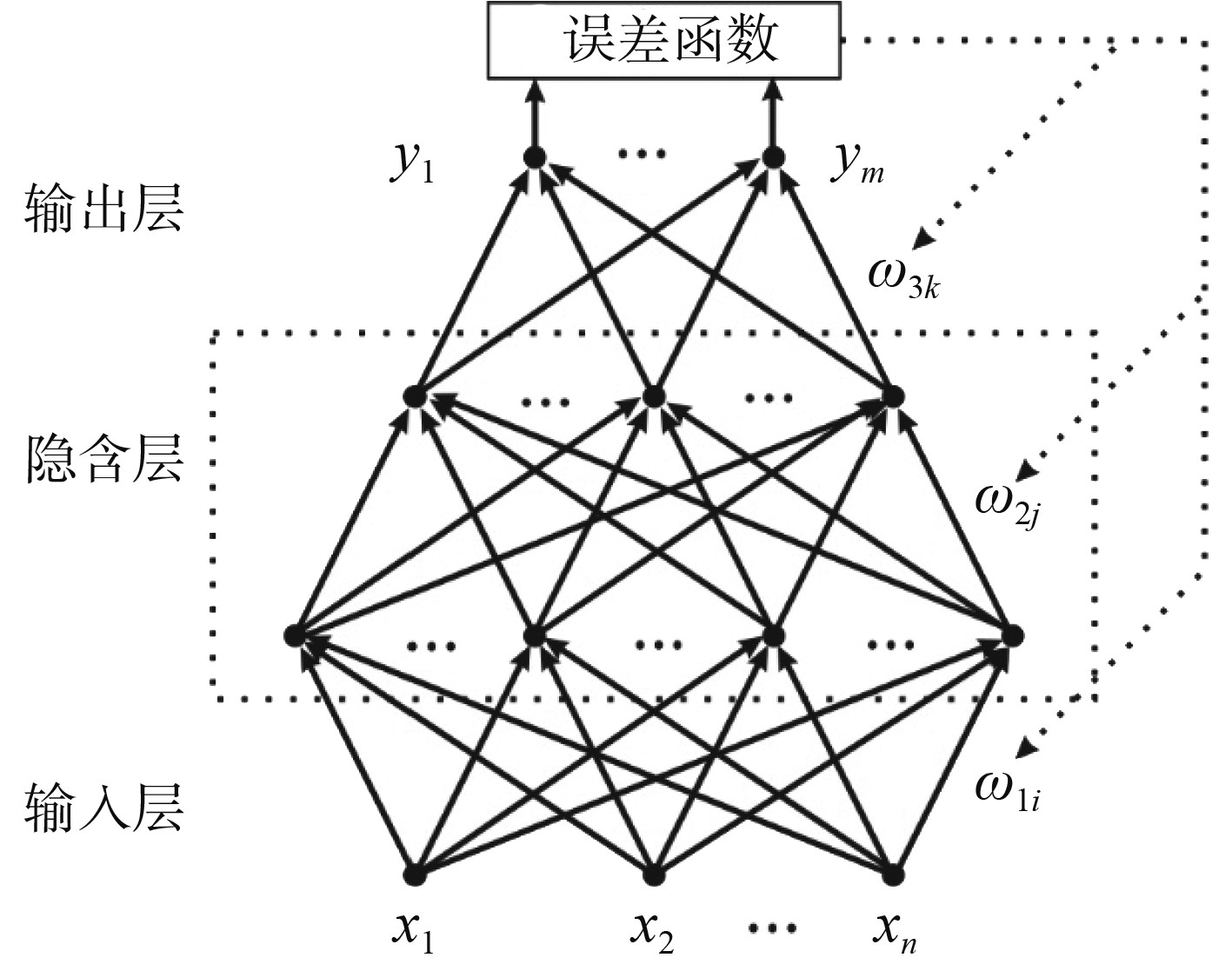
|
图 1 BP神经网络拓扑结构图 Fig. 1 Topological structure of BP neural network |
BP神经网络的学习过程包括信号正向传播和误差反向传播2个部分,首先通过输入层获取原始学习样本,数据经过隐含层建立激活函数,并获取对应权值,最后经输出层输出结果。相邻两层间的传递公式如下式:
| $ y = f(\sum\limits_{i = 1}^n {{\omega _i}{x_i} + a} ){\text{。}} $ | (8) |
式中:x为输入信号,ω为权值,a为偏置,f表示神经网络中的激活函数,y表示数据在本层的输出,也就是下一层的输入。数据在神经网络中传播一轮后,计算误差,对比预先设定的期望结果,若不满足期望,将误差由输出层反向传播至隐含层,其误差传递函数为:
| $ \left\{ {\begin{array}{*{20}{c}} {\omega = \omega - \frac{\mu }{N}\displaystyle\sum\limits_{i = 1}^N {\displaystyle\frac{{\partial E}}{{\partial \omega }}} }{\text{,}} \\ {a = a - \frac{\mu }{N}\displaystyle\sum\limits_{i = 1}^N {\displaystyle\frac{{\partial E}}{{\partial a}}} } 。\end{array}} \right. $ | (9) |
式中:μ为学习率,E为代价函数,通过上述误差传递函数修正神经网络中的权值和偏置,直至满足期望。在计算过程中,为了获取更接近真实问题的神经网络模型,往往需要进行多次的迭代。
基于BP神经网络的磁异常数据延拓方法主要包括如下步骤:
步骤1 样本数据输入。样本数据质量是影响BP神经网络计算结果的重要影响因素。为保证神经网络中数据的准确性和质量,以球体、圆柱体、长方体理论模型在不同高度处的坐标、磁异常及其垂向一阶导数作为样本数据。
步骤2 数据归一化。由于输入数据中包含多种不同单位、量级的参数,为避免较大量级的参数吞没较小量级参数的权重,使激活函数饱和而无法准确获取神经网络模型,需将输入数据进行归一化处理。输入样本的归一化是将各组输入数据数值映射到特定范围内,本文方法是将其映射到[−1,1]的区间内。
步骤3 建立神经网络模型。利用BP神经网络进行位场数据下延在神经网络的应用中实际上算是一个较为简单的问题,并且由于数据样本来源于理论模型,具有很高的精度和准确性,不需要数十万甚至上百万数量级的样本数据,仅需要包含单个隐含层的3层BP神经网络即可进行计算。
步骤4 多次训练获取最优结果。由于BP神经网络在训练及计算过程中的参数是随机生成的,多次训练和计算的结果一般不相同,为获取较为准确的计算结果,取多次计算结果的均值作为最终输出结果。
3 理论模型为验证磁异常数据向下延拓算法的准确性,选取球体与长方体组合模型验证,各模型体平面分布如图2所示。
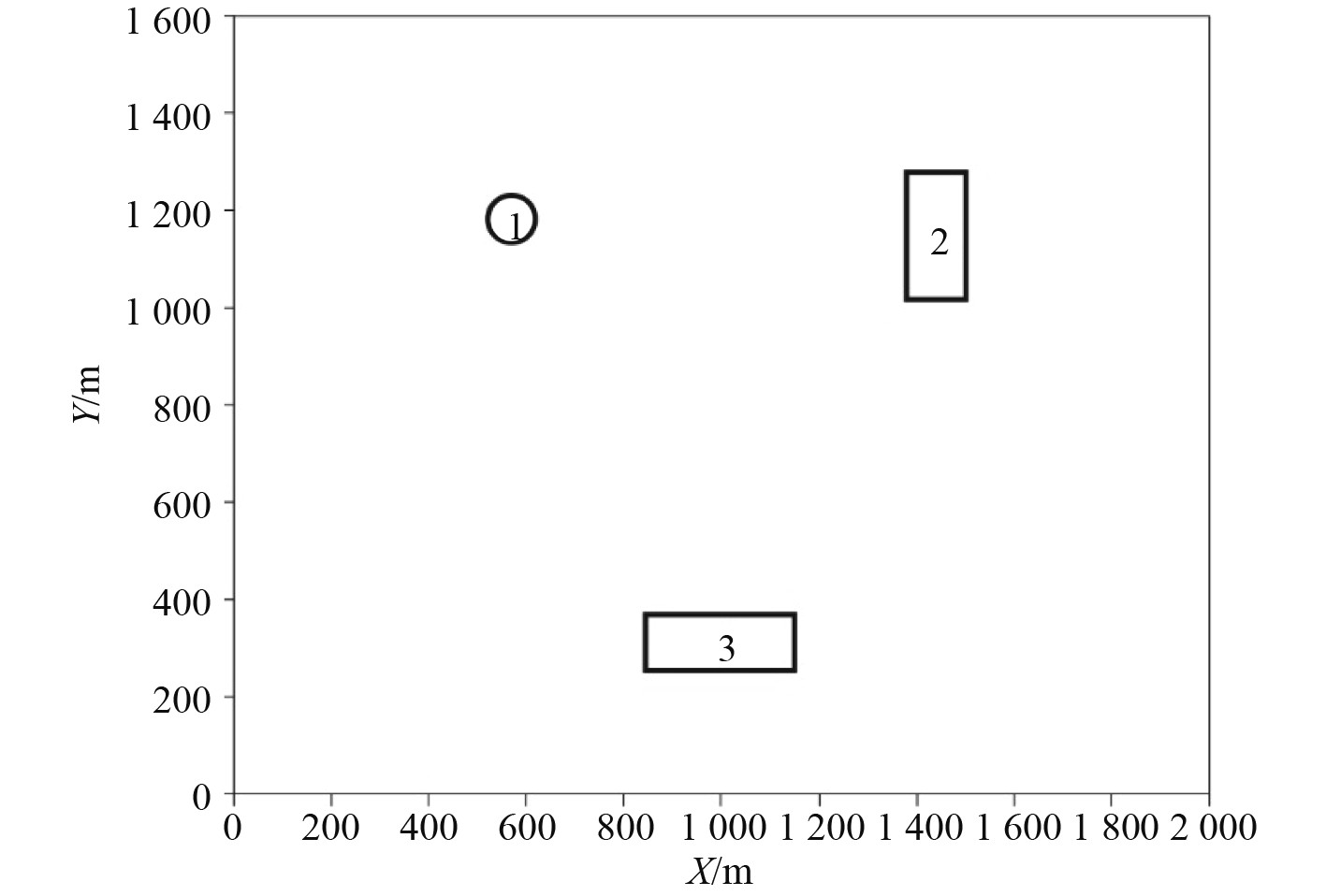
|
图 2 场源平面位置图 Fig. 2 Field source plane location diagram |
该模型由1个球体和2个长方体组成,在北东地空间直角坐标系中,其几何参数见表1。
|
|
表 1 各模型体几何参数表 Tab.1 The geometric parameters of each model body |
3个模型体磁化率为0.03 SI,磁化倾角均为60°,磁化偏角均为30°,地磁场强度为56 000 nT。所选测区x方向范围为(0,2 000 m),y方向范围为(0,1 600 m),测网间距为10 m×10 m。运用球体和长方体正演公式进行计算[18-19],公式如下:
| $ \begin{aligned} & {T_b} = \frac{{{\mu _0}m}}{{4{\text π} {{({x^2} + {y^2} + {h^2})}^{5/2}}}}[(2{h^2} - {x^2} - {y^2}){\sin ^2}I' +\\ & (2{x^2} - {y^2} - {h^2}){\cos ^2}I'{\cos ^2}A' + (2{y^2} - {x^2} - {h^2}){\cos ^2}I'{\sin ^2}A' -\\ & 3xh\sin 2I'\cos A' + 3xy{\cos ^2}I'\sin 2A' - 3yh\sin 2I'\sin A'] {\text{,}} \end{aligned} $ | (10) |
| $\begin{split} {T_r} =& \displaystyle\frac{{{\mu _0}m}}{{4{\text π} }}[{K_1}a\arctan \displaystyle\frac{{\eta + \zeta + R}}{\xi } + \\ &{K_2}a\arctan \displaystyle\frac{{\xi + \zeta + R}}{\eta } + {K_3}a\arctan \displaystyle\frac{{\xi + \eta + R}}{\zeta } + \\ &{K_4}\ln (\xi + R) + {K_5}\ln (\eta + R) + \\ &{K_6}\ln (\zeta + R)\left| {\begin{array}{*{20}{c}} {{\xi _2} - x}\\ {{\xi _1} - x} \end{array}} \right.\left| {\begin{array}{*{20}{c}} {{\eta _2} - y}\\ {{\eta _1} - y} \end{array}\left| {\begin{array}{*{20}{c}} {{\zeta _2} - z}\\ {{\zeta _1} - z} \end{array}} \right|} \right.{。} \end{split}$ | (11) |
式(10)和式(11)分别为球体和长方体磁异常的正演公式。其中,K1=2Ll,K2=2Mm,K3=2Nn,K4=Nm+Mn,K5=Nl+Ln,K6=Ml+Lm;
所选模型体在距地面0 m和300 m处的磁异常如图3所示。
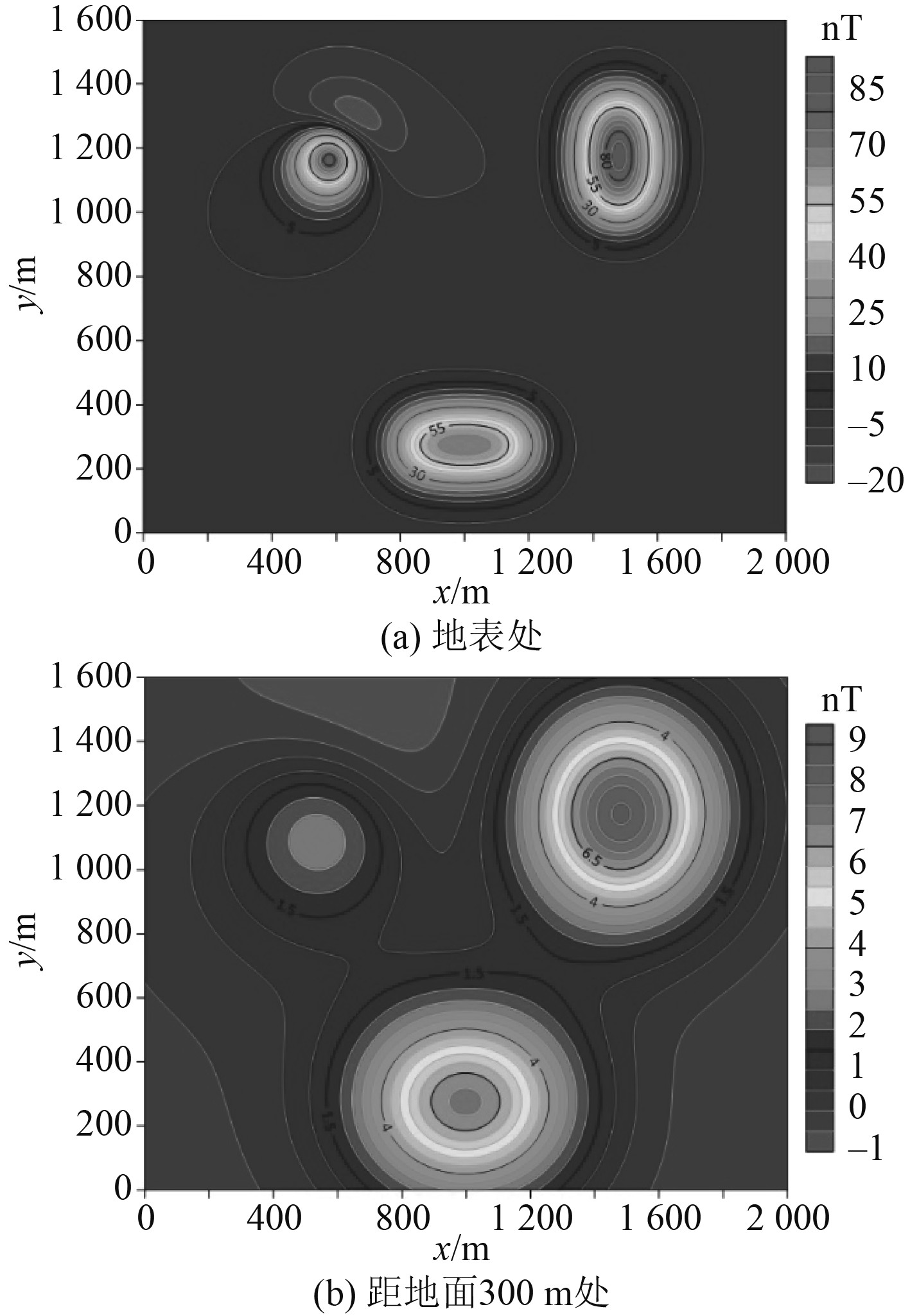
|
图 3 理论模型在0 m和300 m高度处磁异常等值线图 Fig. 3 The contour map of the magnetic anomaly at the height of0 m and 300 m in the theoretical model |
以图3(b)所示磁异常作为原始数据,分别运用积分迭代法和BP神经网络方法将磁异常数据延拓30倍点距至地表处,结果如图4所示。

|
图 4 向下延拓至地表磁异常等值线图 Fig. 4 Contour map of magnetic anomaly extending down to the surface |
其中,积分迭代法最大迭代次数选取为500,每次迭代计算步长为0.01。对比两图,BP神经网络方法具有更准确的量级,且磁异常形态与理论磁异常图3(a)更加接近。图4(a)中球体模型磁异常在下延过程中产生畸变,负异常部分模糊不清。为进一步对比2种方法延拓结果,截取模型2中心点处,即y=1175 m的剖面,2种方法延拓结果如图5所示。

|
图 5 y=1175 m延拓结果磁异常剖面图 Fig. 5 Magnetic anomaly profile of extension results at y=1175 m |
可知,虚线所示的BP神经网络方法更加接近理论磁异常值。当测量数据准确,信噪比较高的情况下,BP神经网络具有比积分迭代方法更稳定的下延结果,并且能够在保证数据精度的前提下稳定下延30倍点距。
在实际磁异常探测时,环境磁噪声的干扰较大。对于向下延拓问题,低信噪比的信号会导致磁异常值不连续,影响向下延拓结果。为模拟实际采集到的磁异常数据,在距地面高度300 m处的磁异常数据中加入图6(a)所示的高斯白噪声,噪声峰值为0.5 nT,加入噪声后的磁异常等值线图如图6(b)所示。
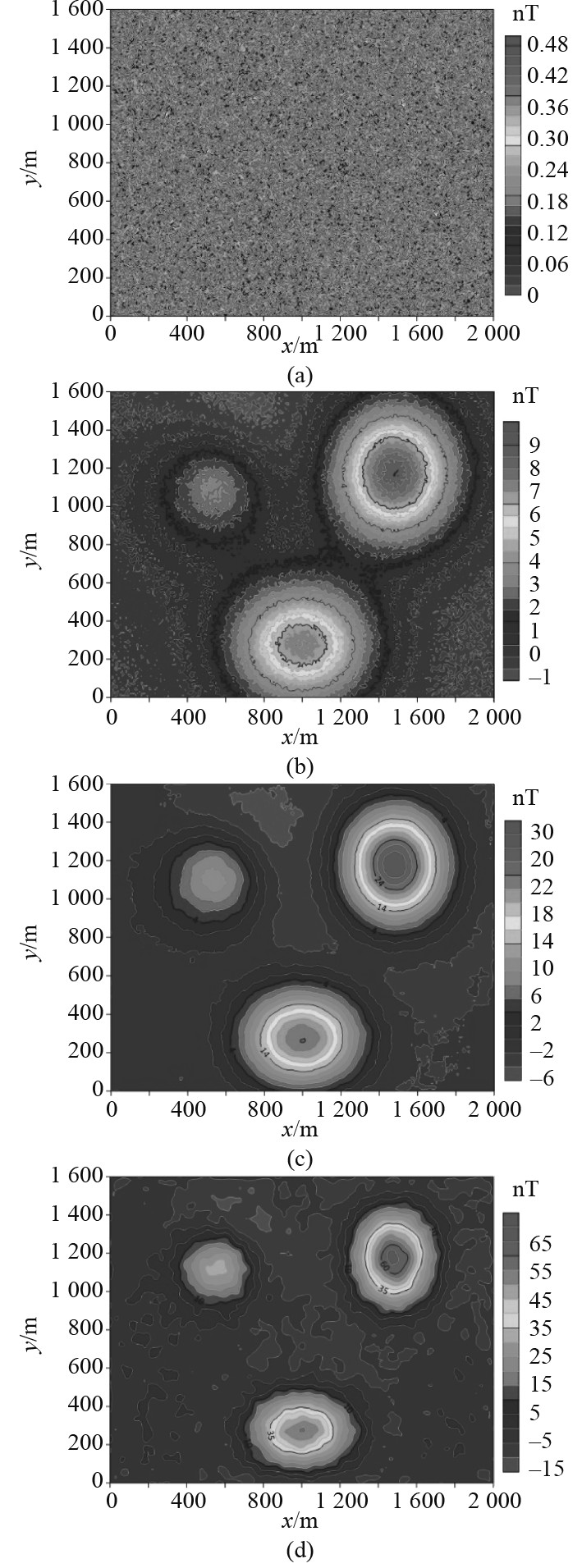
|
图 6 含噪磁异常数据的向下延拓 Fig. 6 Downward continuation of noisy magnetic anomaly data |
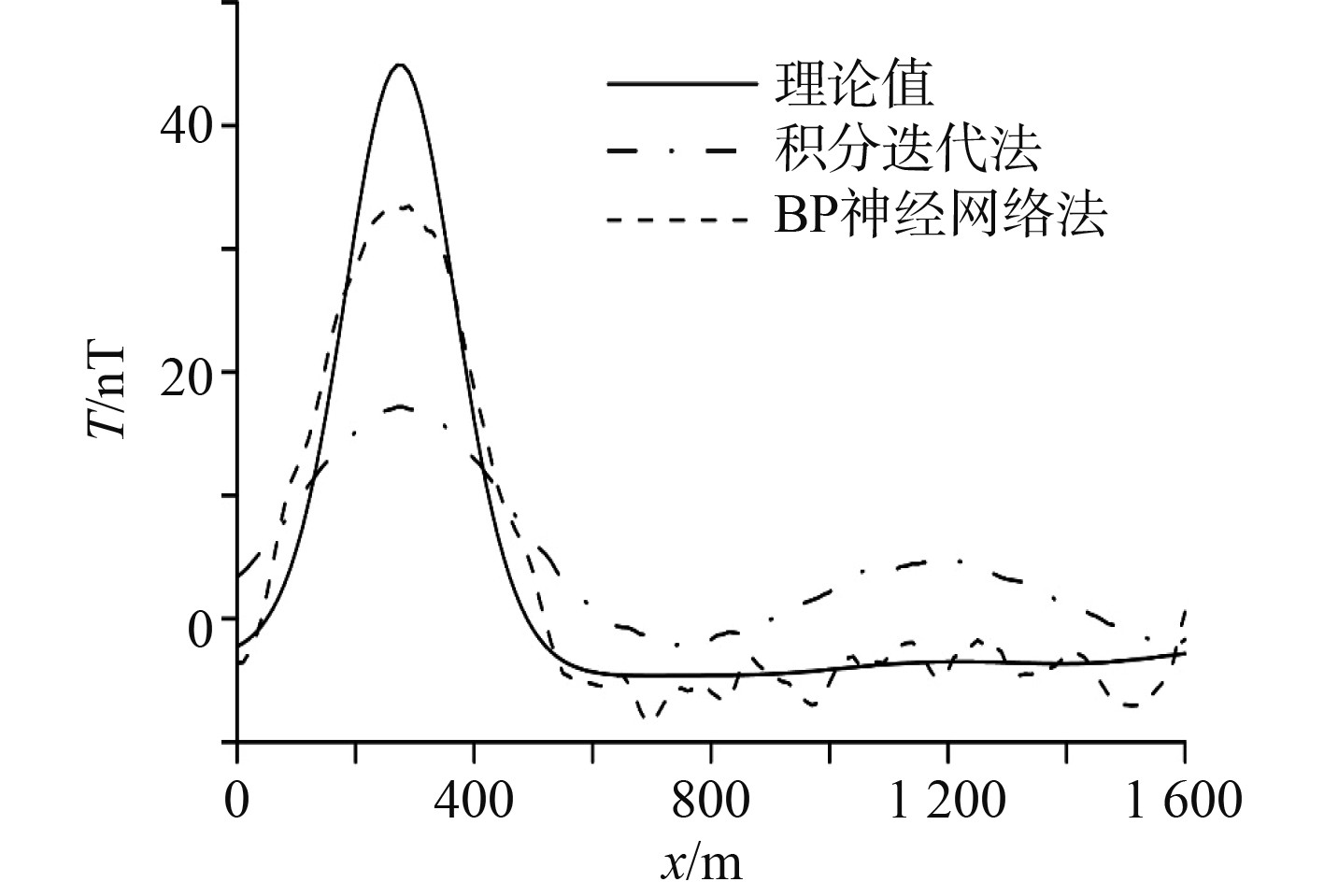
依旧运用上述2种方法将含0.5 nT高斯白噪声的磁异常数据向下延拓至地表处,保持原有计算参数不变,运用积分迭代法计算结果如图6(c)所示,运用BP神经网络方法的延拓结果如图6(d)所示。对比可知,2种方法延拓结果均不存在较严重的畸变,能够分离3个模型磁异常。仍然截取模型2中心点所在的y=1175处的截面,2种延拓方法结果如图7所示。
|
图 7 y=1175 m延拓结果磁异常剖面图 Fig. 7 Magnetic anomaly profile of extension results at y=1175 m |
图中,总体上虚线所示的BP神经网络方法延拓结果更贴近理论磁异常值,但在曲线右侧具有稍大的波动。BP神经网络方法的延拓结果具有更接近真实地表磁异常值的量级,且磁异常大小形态也更接近于理论地表处的磁异常,但含有稍多的噪声。
为直观对比2种方法延拓精度,假设理论模型磁异常值为xt,运用向下延拓方法计算的磁异常值为xc,则延拓结果的均方误差为:
| $ RMSE = \sqrt {\frac{1}{{MN}}{{\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {[{x_c} - {x_t}]^2} } }}}{\text{,}} $ | (12) |
相关性误差为:
| $ RE = \dfrac{{{{\left\| {{x_c} - {x_t}} \right\|}_2}}}{{{{\left\| {{x_t}} \right\|}_2}}}{\text{。}} $ | (13) |
2种方法延拓误差如表2所示。
|
|
表 2 积分迭代法与BP神经网络方法的均方误差和相关性误差表 Tab.2 Mean square error and correlation error table of integral iteration method and BP neural network method |
可知,无论是无噪声的数据还是含噪声的数据,BP神经网络方法均具有更小的误差,该方法能够稳定延拓30倍点距。
5 结 语本文研究意义在于将实测航磁数据向下延拓至海平面高度,代替船测磁异常数据,弥补船测磁异常测量效率低、成本高等缺点。有效解决了现有磁异常向下延拓方法有效延拓高度不足,强行进行20倍以上点距延拓畸变严重的问题
1)提出基于BP神经网络的向下延拓方法,构建由球体和长方体组成的混合模型,通过球体及长方体磁异常正演公式计算不同高度处的磁异常理论数据,采用当前较常用的积分迭代法,对比本文提出的BP神经网络方法。结果表明,基于BP神经网络的向下延拓方法具有更加准确的结果,能够进行30倍点距的稳定下延。
2)模型试验中,BP神经网络方法在高质量信号的条件下具有很好效果,能够进行多倍点距下延,但仍存在一些问题。当信号中噪声较强时,本身磁场信号较弱的区域会存在干扰,这部分区域的延拓结果并不理想,后续将针对这一问题开展研究。
| [1] |
董鹏, 孙哲, 邹念洋, 等. 国外磁探潜装备现状及发展趋势[J]. 舰船科学技术, 2018, 40(21): 166–169. DONG P, SUN Z, ZOU N Y, et al. The situation and development trend of foreign magnetic exploration submarine equipment[J]. Ship Science and Technology, 2018, 40(21): 166–169. |
| [2] |
王光辉, 朱海, 郭正东, 等. 舰船感应磁性的磁异常信号特征[J]. 舰船科学技术, 2015, 37(9): 137-139. WANG Guang-hui, ZHU Hai, GUO Zheng-dong, et al. MAD signal character of ship's induced magnetism[J]. Ship Science and Technology, 2015, 37(9): 137-139. |
| [3] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005: 85–100.
|
| [4] |
焦新华, 吴燕冈. 重力与磁力勘探[M]. 北京: 地质出版社, 2009: 190–195.
|
| [5] |
于德武, 龚胜平. 对迭代法位场向下延拓方法的剖析[J]. 吉林大学学报(地球科学版), 2015, 45(3): 934–940. YU D W, GONG S P. Analysis of the potential field downward continuation iteration method[J]. Journal of Jilin University(Earth Science Edition) , 2015, 45(3): 934-940. |
| [6] |
尹伟言, 陈真, 蒋涛, 等. 地面重力数据向上延拓方法比较[J]. 地理空间信息, 2018, 16(7): 75-76+95+10. YIN W Y, CHEN Z, JIANG T, et al. Comparison of upward continuation methods for ground gravity data[J]. Geospatial Information, 2018, 16(7): 75-76+95+10. |
| [7] |
周智文, 何水原, 孟小红, 等. 约束等效源稳定向下延拓方法研究[J]. 地球物理学报, 2022, 65(2): 754–762. ZHOU Z W, HE S Y MENG X H, et al. Stable downward continuation of potential field data using an equivalent sourse method and a constrained strategy[J]. Chinese Journal of Geophysics, 2022, 65(2): 754–762. |
| [8] |
赵亚博, 刘天佑. 迭代Tikhonov正则化位场向下延拓方法及其在尕林格铁矿的应用[J]. 物探与化探, 2015, 39(4): 743-748. ZHAO Y B, LIU T Y. The iterative Tikhonov regularization method for downward continuation of potential fields and its application to the Galinge iron deposit[J]. Geophysical and Geochemical Exploration, 2015, 39(4): 743-748. |
| [9] |
EVJEN H M. The place of the vertical gradient in gravitational interpretations[J]. Geophysics, 2002, 1(1): 127-136. |
| [10] |
PETERS L J. The direct approach to magnetic interpretation and its practical application[J]. Geophysics, 1949, 14(3): 290-320. DOI:10.1190/1.1437537 |
| [11] |
DEAN W C. Frequency analysis for gravity and magnetic interpretaion[J]. Geophysics, 2002, 23(1): 97-127. |
| [12] |
FEDI M, FLORIO G. A stable downward continuation by using the ISVD method[J]. Geophysical Journal International, 2002, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
| [13] |
徐世浙. 位场延拓的积分-迭代法[J]. 地球物理学报, 2006(4): 1176-1182. XU S Z. The integral-iteration method for continuation of potential fields[J]. Chinese Journal of Geophysics, 2006(4): 1176-1182. DOI:10.3321/j.issn:0001-5733.2006.04.033 |
| [14] |
徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报, 2007(1): 285-289. XU S Z. A comparison of effects between the iteration method and FFT for downward continuation of potential fields[J]. Chinese Journal of Geophysics, 2007(1): 285-289. DOI:10.3321/j.issn:0001-5733.2007.01.035 |
| [15] |
刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报, 2009, 52(6): 1599-1605. DOI:10.3969/j.issn.0001-5733.2009.06.022 |
| [16] |
于波, 翟国君, 刘雁春, 等. 噪声对磁场向下延拓迭代法的计算误差影响分析[J]. 地球物理学报, 2009, 52(8): 2182-2188. DOI:10.3969/j.issn.0001-5733.2009.08.029 |
| [17] |
曾小牛, 李夕海, 韩绍卿, 等. 位场向下延拓三种迭代方法之比较[J]. 地球物理学进展, 2011, 26(3): 908-915. ZENG X N, LI X H, HAN S Q, et al. A comparison of three iteration methords for downward continuation of potential fields[J]. Progress in Geophysics, 2011, 26(3): 908-915. DOI:10.3969/j.issn.1004-2903.2011.03.016 |
| [18] |
钟炀, 管彦武, 石甲强, 等. 长方体全张量磁梯度的两种正演公式对比[J]. 世界地质, 2019, 38(4): 1073-1081+1090. DOI:10.3969/j.issn.1004-5589.2019.04.018 |
| [19] |
骆遥, 姚长利. 长方体磁场及其梯度无解析奇点表达式理论研究[J]. 石油地球物理勘探, 2007, 42(6): 714-719. LUO Y, YAO C L. Theoretical study on cuboid magnetic field and gradient expression without singular point[J]. Oil Geophysical Prospecting, 2007, 42(6): 714-719. DOI:10.3321/j.issn:1000-7210.2007.06.019 |
 2023, Vol. 45
2023, Vol. 45
