轴承是安装在船舶上的承受载荷和转动力的机械装置。轴承具有承载能力强、摩擦系数低、耐磨性好等特点,能够保证船舶在航行过程中的稳定性和安全性。轴承的选用要考虑到船舶的使用环境和工作条件,如船舶的航行速度、载荷大小、工作温度等因素。此外,轴承的维护保养也非常重要,定期检查和更换轴承,保证其正常运转,延长其使用寿命。
船舶机械轴承的故障监测技术是近年来的研究热点,目前常用的船舶轴承故障监测手段包括振动监测、温度监测、声音监测和油液监测。
振动监测:通过安装振动传感器在轴承上监测振动信号,通过分析振动频谱和振动特征参数,可以判断轴承的工作状态和故障类型。
温度监测:通过安装温度传感器在轴承上监测轴承温度变化,当温度异常时可以判断轴承是否存在故障。
声音监测:通过安装声音传感器在轴承上监测轴承工作时的声音信号,通过分析声音频谱和声音特征参数,可以判断轴承的工作状态和故障类型。
油液监测:通过监测轴承润滑油的温度、压力、粘度等参数,可以判断轴承的润滑状态和故障情况。
本文针对船舶机械轴承故障监测技术,提出基于小波变换和变分模态分解(VMD)的信号处理方法,结合小波神经网络实现了船舶机械轴承故障的信号处理和预测。
1 船舶机械轴承特性及故障分析为了对船舶轴承故障信号进行数学建模,针对船舶机械设备最常用的滚动轴承进行建模分析。
滚动轴承是固定转轴和其他零部件相对位置的部件,通常由内圈、外圈、滚珠和保持架组成,如图1所示。

|
图 1 滚动轴承的结构示意图 Fig. 1 Structure diagram of rolling bearing |
船舶滚动轴承常见的失效形式包括[1]:
1)疲劳失效
长期受到往复载荷作用,导致滚道和滚珠或滚子表面出现疲劳裂纹,最终导致断裂。
2)磨损失效
由于滚道和滚珠或滚子之间的摩擦和磨损,导致滚道表面磨损、凹坑和滚珠或滚子表面磨损、变形。
3)过载失效
当滚动轴承承受超过其额定负荷的载荷时,会导致滚珠或滚子和滚道之间的接触压力过大,从而引起滚珠或滚子和滚道的塑性变形或断裂。
4)温度过高失效
由于滚动轴承在工作过程中摩擦产生热量,如果无法及时散热,会导致温度升高,从而引起润滑剂失效、材料膨胀、变形等问题。
轴承发生故障的位置以内圈、外圈和滚动体为主。
1)滚动轴承的内圈故障
当轴承内圈发生故障时,不正常的转动会导致振动冲击,产生径向载荷,内圈故障的特征频率计算式为:
| $ f_{n1}=\frac{Z}{2}\cdot\frac{r}{60}\left(1-\frac{d}{D}\cos\alpha\right)\text{。} $ |
式中:Z为滚动体的个数,r为滚动轴承转速,d为滚动体的直径,D为滚动轴承的节圆直径,
轴承故障频率往往为高频,通过滤波器进行低频滤波,可以得到轴承故障频谱,如图2所示。

|
图 2 轴承故障高通滤波和故障频谱 Fig. 2 Bearing faults, high-pass filtering and fault spectrum |
2)滚动体故障
滚动体故障是船舶轴承最为常见的一种故障,伴随着轴承过温、异响、振动冲击等,滚动体故障的特征频率计算式为:
| $ {f_{n2}} = \frac{Z}{2} \cdot \frac{r}{{60}}\left( {1 - {{\left( {\frac{d}{D}\cos \alpha } \right)}^2}} \right) \text{。} $ |
3)外圈故障
由于滚动轴承外圈固定在轴承座上,因此,当外圈出现故障时,发生冲击载荷的位置是固定的,信号特征频率为:
| $ {f_{n3}} = \frac{Z}{2} \cdot \frac{r}{{60}}\left( {1 + {{\left( {\frac{d}{D}\cos \alpha } \right)}^2}} \right) \text{。} $ |
变分模态分解(VMD)是一种频域的信号分析方法,与滤波算法和傅里叶变换等相结合,能够实现信号的准确解析。VMD是基于变分贝叶斯方法[2],它被用于将复杂的非平稳信号分解成一系列模态函数,通过最小化信号与模态函数之间的差异来实现信号分解。VMD首先将信号分解成多个频带,每个频带包含一组频率和幅度。然后,通过迭代优化的方式,确定每个频带的中心频率和带宽,以及每个频带中的模态函数。最后,将所有的模态函数求和,得到原始信号的近似重构。
VMD的优点在于能够处理非平稳信号,适用于各种信号分析和处理任务。它可以用于信号去噪、频谱分析、模态分解等应用领域。VMD还具有较好的自适应性,可以根据信号的特性自动选择合适的参数。
对信号
1)假设信号有k个固有模态函数
2)建立固有模态函数
| $ h\left(t\right)=\left(\delta\left(t\right)+\frac{j}{\text{π}\sqrt{2}t}\right)\cdot u_k\left(t\right)\text{。} $ |
3)对信号进行频谱调制,公式如下:
| $ \Gamma\left(t\right)=\left[\left(\delta\left(t\right)+\frac{j}{{\text{π}} \sqrt{2}t}\right)\cdot u_k\left(t\right)\right]e^{-jwt}\text{。} $ |
4)对调制的信号进行高斯变换:
| $ \left\{ \begin{gathered} \min \left\{ {} \right.\displaystyle\sum\limits_k^{} {\left| {\frac{\partial }{{\partial t}}} \right.} \left( {\delta \left( t \right) + \dfrac{j}{{{\text{π}} \sqrt 2 t}}} \right) \cdot {u_k}\left( t \right){w_k}\left( t \right)\left. {} \right\},\\ \displaystyle\sum\limits_k^{} {{u_k}\left( t \right) = f\left( t \right)}。\\ \end{gathered} \right. $ |
式中:
5)基于拉格朗日算子
| $\begin{split} B({u_k}\left( t \right),{w_k}\left( t \right)) =& \lambda \left( t \right) \cdot \min \left\{ {} \right.\sum\limits_k^{} {\left| {\frac{\partial }{{\partial t}}} \right.}\cdot \\&\left( {\delta \left( t \right) + \frac{j}{{{\text{π}}\sqrt 2 t}}} \right)\cdot {u_k}\left( t \right){w_k}\left( t \right)\left. {} \right\} \text{。} \end{split}$ |
图3为基于VMD算法的函数迭代示意图。
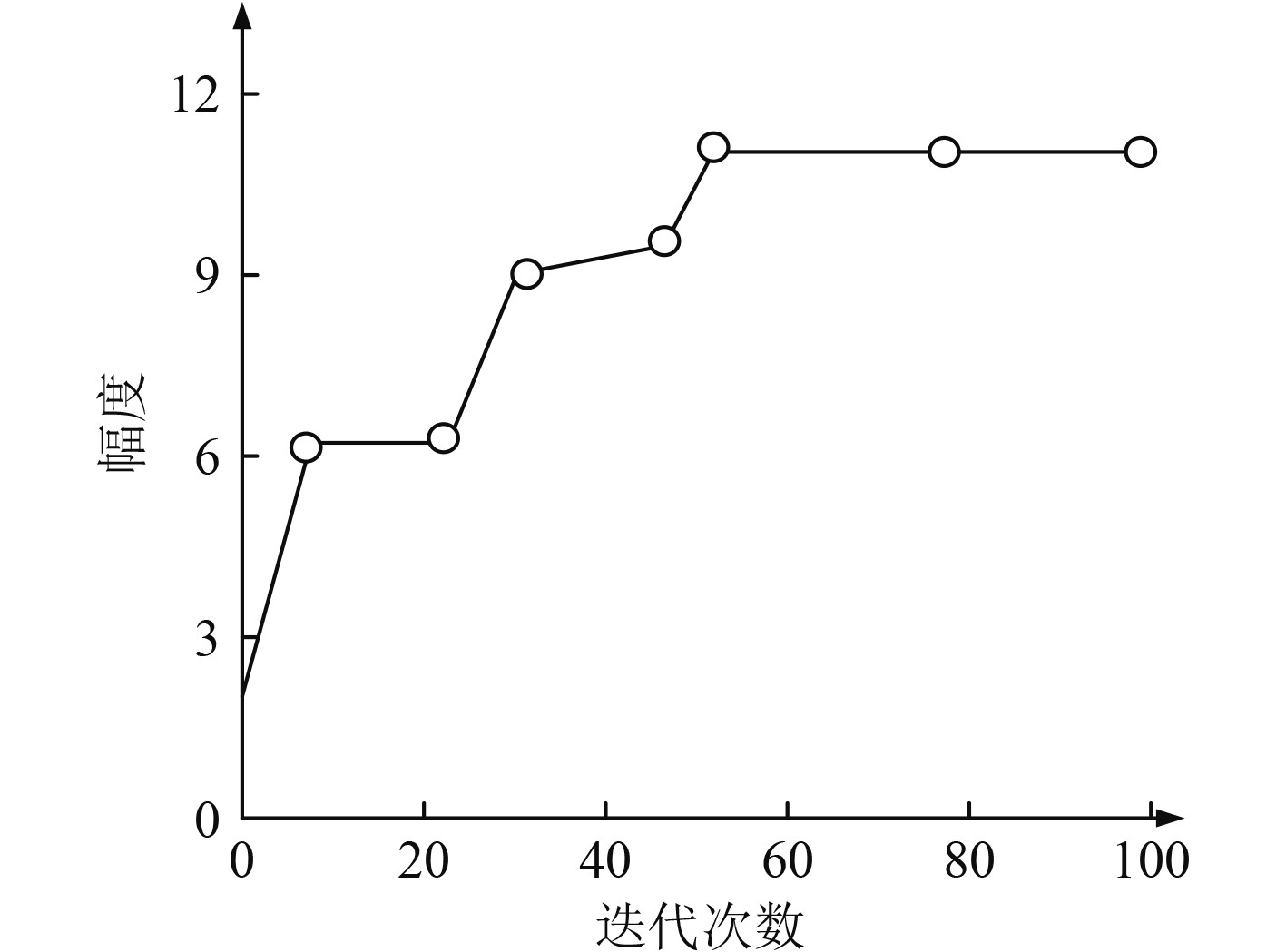
|
图 3 基于VMD算法的函数迭代示意图 Fig. 3 Function iteration diagram based on VMD algorithm |
可知,基于VMD模态分解在60次的迭代次数附近,幅值不再发生变化,达到函数收敛,可见VMD模态分解算法的求解效率相对较高。
2.2 多分辨小波变换理论多分辨小波变换分析基于小波函数的多尺度分析能力,可以将信号分解成不同尺度的频带[3],并在不同尺度上对信号进行分析。在信号分解步骤中,信号经过一系列低通和高通滤波器的处理,得到不同尺度的频带系数。低通滤波器用于提取低频信息,高通滤波器用于提取高频信息。在重构步骤中,通过逆滤波器和逆小波变换,将频带系数重构为原始信号。
对于某非线性信号
| $ \int\limits_R^{} {} {\left| {\frac{{x\left( \omega \right)}}{\omega }} \right|^2}{\rm{d}}\omega \leqslant \infty \text{。} $ |
式中:
信号
| $ {x_s}\left( t \right) = \frac{1}{{\sqrt s }}x\left( {\frac{{t - \alpha }}{s}} \right) \text{。} $ |
式中:s为伸缩变换因子,
信号的傅里叶变换为
| $ \begin{split} W{T_f}\left( {s,t} \right) =& \left\{ {f\left( t \right),x\left( t \right)} \right\}= \\ &\frac{1}{{\sqrt s }}\int\limits_{}^{} {f\left( t \right)} x\left( {\frac{{t - \alpha }}{s}} \right){\rm{d}}t \end{split}\text{。} $ |
常见的小波函数有:
1)Harr小波函数
Harr小波函数的性质包括平移不变性、尺度不变性和正交性,这些性质使得Harr小波函数在信号压缩、图像处理和数据压缩等领域有着广泛的应用。表达式如下:
| $ H\left( t \right) = \left\{ \begin{array}{ll} 1,&0 < t < \dfrac{1}{2} ,\\ - 1,&\dfrac{1}{2} < t < 1,\\ 0,&{\rm{else}}。 \end{array} \right. $ |
2)Morlet小波函数
Morlet小波函数的形状类似于一个复指数函数,同时具有高斯包络。它的实部表示信号的振幅变化,虚部表示信号的相位变化。通过对信号进行Morlet小波变换,可以得到信号在不同频率上的振幅和相位信息,从而实现信号的时频分析。模型如下:
| $ \psi \left( t \right) = C{e^{\tfrac{{{t^2}}}{2}}}\cos \left( {5t} \right) \text{。} $ |
本文结合模糊神经网络算法和VMD算法,建立一种船舶轴承故障预测系统,该系统的原理如图4所示。
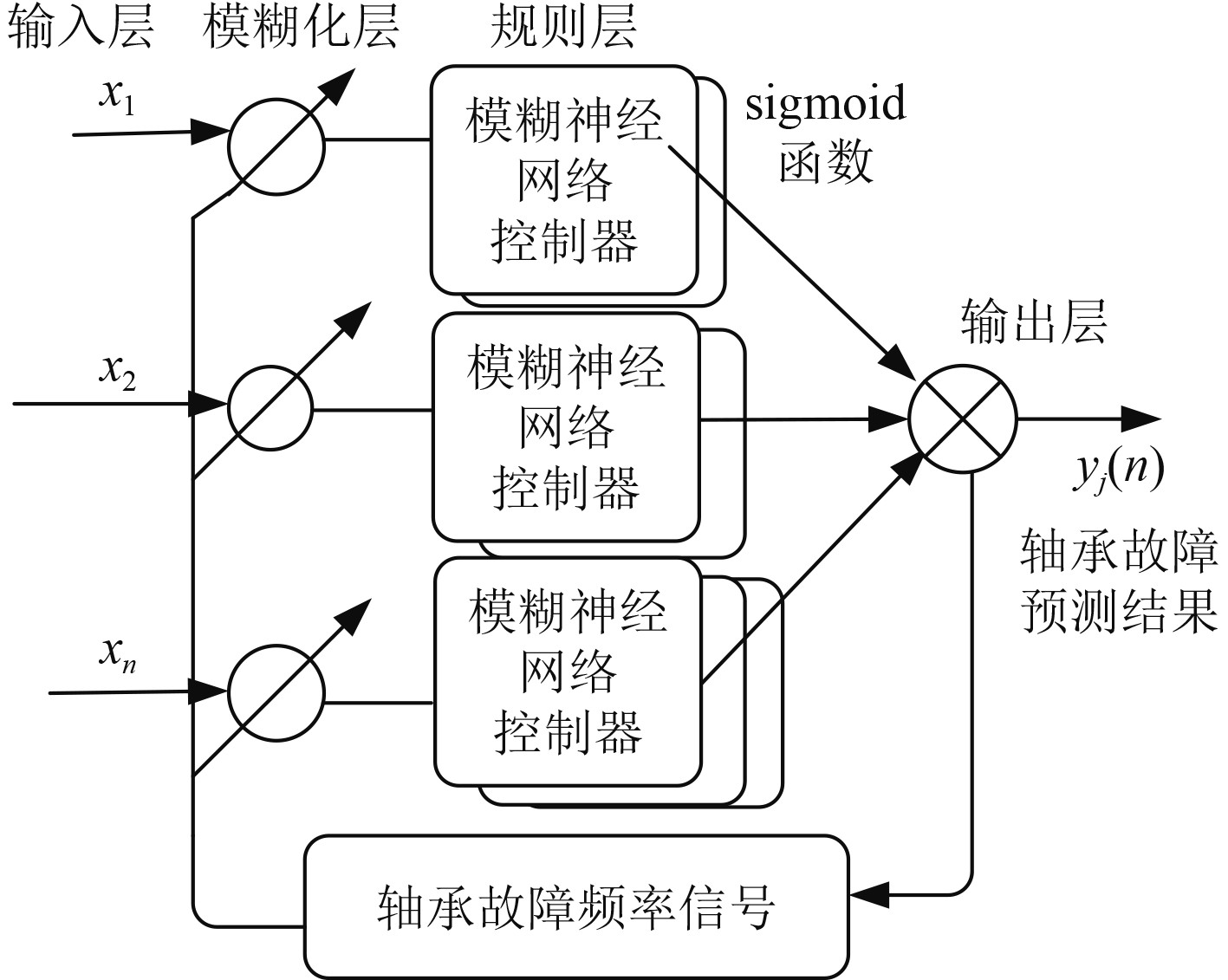
|
图 4 基于神经网络和VMD的轴承故障预测原理 Fig. 4 Bearing failure prediction principle based on neural network and VMD |
基于模糊神经网络和VMD的轴承故障预测步骤如下:
步骤1 网络的初始化。
步骤2 输入信号的小波变换。
输入信号为轴承振动信号
| $ \int\limits_R^{} {} {\left| {\frac{{x\left( \omega \right)}}{\omega }} \right|^2}{\rm{d}}\omega \leqslant \infty \text{。} $ |
步骤3 神经元的距离计算,如下式:
| $ {d_i} = \left| {{X_j} - {X_i}} \right| = \sqrt {\left( {\sum\limits_{i = 1}^m {{{\left( {{x_i}\left( t \right) - {w_i}\left( t \right)} \right)}^2}} } \right)} \text{。} $ |
式中,
步骤4 故障预测。
建立系统的故障预测模型为:
| $ F\left( {s,t} \right) = \left\{ {x\left( t \right)} \right\}\; = \dfrac{1}{{\sqrt 2 }}\left[ {\dfrac{{\displaystyle\sum\limits_{j = 1}^n {} {\omega _j}\left( n \right) - {a_j}}}{{{b_j}}}}\right] {。} $ |
式中:
为了验证本文提出的故障预测方法的有效性,搭建船舶轴承的故障预测测试平台,如图5所示。

|
图 5 船舶轴承的故障预测测试平台 Fig. 5 Failure prediction test platform for ship bearings |
测试平台包括电源输入、联轴器、滑动轴承、转速显示单元、负载控制、变速驱动电机[4]等。
设定电机转速2000 r/min,采样频率20 kHz,时间历程1200 s,得到轴承故障频谱如图6所示。
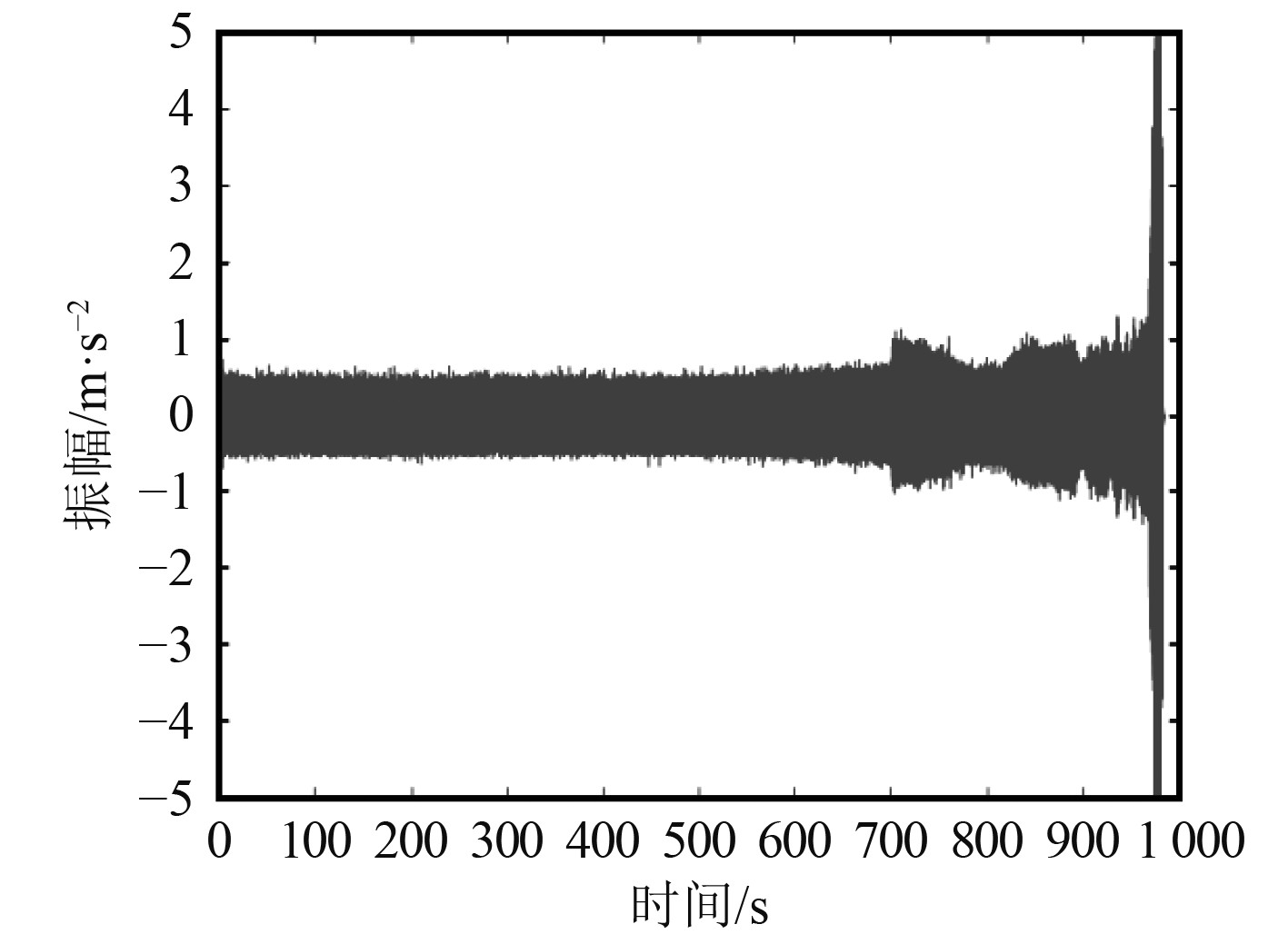
|
图 6 轴承故障频谱 Fig. 6 Spectrum of bearing failures |
可知,在1000 s左右出现明显的故障频率,振动幅值明显增加。
3 结 语针对船舶轴承的运行可靠性,本文结合模糊神经网络和VMD模态分解算法,从轴承的故障频率建模出发,建立了船舶轴承的故障预测和诊断系统,并通过试验台测试验证了方法的有效性。
| [1] |
贾萌珊, 齐子元, 薛德庆, 等. 基于GASA-BP-BiLSTM的轴承故障预测研究[J]. 组合机床与自动化加工技术, 2023(5): 148−151+155.
|
| [2] |
朱伏平, 秦琴, 杨方燕, 等. 基于信息融合技术的滚动轴承故障预测方法[J]. 机械设计, 2023, 40(1): 56-64. |
| [3] |
刘桂然. 基于BP-神经网络的风电主轴承故障预测[J]. 科学技术创新, 2020(26): 18-19. DOI:10.3969/j.issn.1673-1328.2020.26.009 |
| [4] |
李泓洋, 万烂军, 李长云, 等. 基于神经网络和证据理论的滚动轴承故障预测方法[J]. 湖南工业大学学报, 2020, 34(4): 35-41. DOI:10.3969/j.issn.1673-9833.2020.04.006 |
 2023, Vol. 45
2023, Vol. 45
