无刷直流电机由电机、位置传感器、线路等组成,通过电子换相的方式驱动电机运行,可靠性高,被广泛应用在工业领域[1]。目前,我国在大型舰船中使用无刷直流电机,控制大型舰船的行驶速度,保障大型舰船安全[2]。但因无刷直流电机结构的特殊性,其平均转矩会高于普通电机的平均转矩,在运行过程中容易出现转矩脉动问题[3]。若转矩脉动问题不能及时解决,会引起无刷直流电机故障,威胁大型舰船的安全。因此,对大型舰船用无刷直流电机转矩脉动抑制方法的课题研究至关重要,相关学者已经对该课题研究。李珍国等[4]研究转子定向抑制方法,构建电机磁场等效模型,但该方法的计算量比较大,导致转矩脉动抑制效率较低。陆可等[5]研究电压矢量的抑制方法,但该方法对电机零速运行时脉动抑制效果不佳。因上述方法的局限性,研究开通角的大型舰船用无刷直流电机转矩脉动抑制方法,消除转矩脉动,提高无刷直流电机使用寿命。
1 船用无刷直流电机转矩脉动抑制方法 1.1 船用无刷直流电机数学模型船用无刷直流电机的电路结构[6]如图1所示。图中,
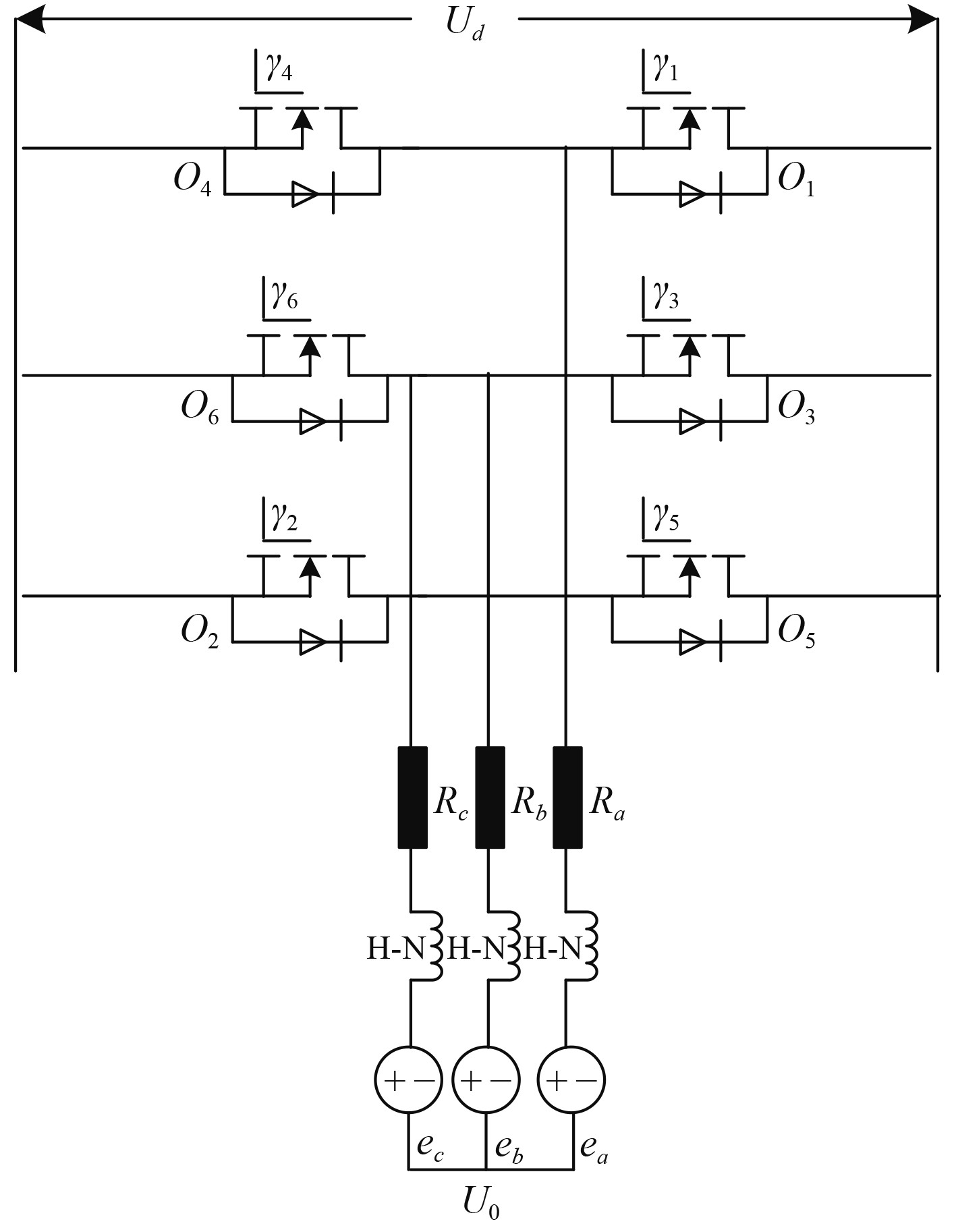
|
图 1 船用无刷直流电机的电路结构 Fig. 1 Circuit structure of brushless DC motor for ships |
三相电流关系表达式如下:
| $ {i_c} + {i_b} + {i_a} = 0 。$ | (1) |
依据Kirchhoff定律构建三相电压公式为:
| $ \left\{ \begin{gathered} {U_d} \times {z_a} = {U_0} + R{i_a} + \eta \left( {d{i_a}/dt} \right) + {e_a} ,\\ {U_d} \times {z_b} = {U_0} + R{i_b} + \eta \left( {d{i_b}/dt} \right) + {e_b} ,\\ {U_d} \times {z_c} = {U_0} + R{i_c} + \eta \left( {d{i_c}/dt} \right) + {e_c} 。\\ \end{gathered} \right. $ | (2) |
式中:za、zb、zc分别描述三相电流开关函数;
将式(2)内3个方程相加,并结合式(1)求出电机中性点U0,其表达式为:
| $ {U_0} = {U_d} \times \left[ {\left( {{z_a} + {z_b} + {z_c}} \right)/3} \right] - \left[ {\left( {{e_a} + {e_b} + {e_c}} \right)/3} \right] 。$ | (3) |
把式(3)导入式(2),得出三相电静止坐标系公式如下:
| $ \left\{ \begin{gathered} \eta \left( {{\rm{d}}{i_a}/{\rm{d}}t} \right) = - R{i_a} + {U_d} \times {Z_A} + {E_A},\\ \eta \left( {{\rm{d}}{i_b}/{\rm{d}}t} \right) = - R{i_b} + {U_d} \times {Z_B} + {E_B} ,\\ \eta \left( {{\rm{d}}{i_c}/{\rm{d}}t} \right) = - R{i_c} + {U_d} \times {Z_C} + {E_C}。\\ \end{gathered} \right. $ | (4) |
式中:
将三相向二相静止坐标系转换的公式如下:
| $ \left\{ \begin{gathered} \eta \left( {{\rm{d}}{i_\alpha }/{\rm{d}}t} \right) = - R{i_\alpha } + {U_d} \times {Z_\alpha } + {E_\alpha } \\ \eta \left( {{\rm{d}}{i_\beta }/{\rm{d}}t} \right) = - R{i_\beta } + {U_d} \times {Z_\beta } + {E_\beta } \\ \end{gathered} \right. $ | (5) |
式中:
依据电机理论[6],机械转动惯量用
| $ J\left( {{\rm{d}}\chi /{\rm{d}}t} \right) = {T_e} - {S_v}\chi - T_H^{}。$ | (6) |
式中:TH为负载转矩;Te为电磁转矩;
电磁转矩公式如下:
| $ {T_e} = p\left( {{e_a}{i_a} + {e_b}{i_b} + {e_c}{i_c}} \right)/\chi = {F_T} \times \phi \times I 。$ | (7) |
其中:
在船用无刷直流电机数学模型基础上,分析无刷直流电机的换相过程中电流变化情况,AB导通向AC导通换相过程为例,此时
| $ \left\{\begin{array}{l} {e}_{a}-{e}_{b}+2\left(H-N\right)\left(\text{d}{i}_{1}/\text{d}t\right)+\left(H-N\right)\left(\text{d}{i}_{2}/\text{d}t\right)+2R{i}_{1}=0,\\ {e}_{a}-{e}_{c}+2\left(H-N\right)\left(\text{d}{i}_{1}/\text{d}t\right)+\left(H-N\right)\left(\text{d}{i}_{2}/\text{d}t\right)+R{i}_{1}={U}_{d},\\ {i}_{a}={i}_{1}+{i}_{2}\text{,}{i}_{b}=-{i}_{1}\text{,}{i}_{c}=-{i}_{2}。\end{array}\right. $ | (8) |
设置平底波最高幅值用
| $ \left\{ \begin{gathered} \left( {{\rm{d}}{i_b}/{\rm{d}}t} \right) = - R\left( {H - N} \right){i_b} + \left[ {\left( {2\varGamma + {U_d}} \right)/3\left( {H - N} \right)} \right],\\ \left( {{\rm{d}}{i_c}/{\rm{d}}t} \right) = - R\left( {H - N} \right){i_c} + \left[ {\left( {2{U_d} - 2\varGamma } \right)/3\left( {H - N} \right)} \right] 。\\ \end{gathered} \right. $ | (9) |
换相开始时ib、ic状态表达式如下:
| $ \left\{\begin{array}{l}{i}_{b}={f}_{1}\left(\varepsilon \right)\text{,}{i}_{c}={f}_{2}\left(\varepsilon \right),\\ \varepsilon =0{,}^{}{i}_{b}=-I,{i}_{c}=0。\end{array}\right. $ | (10) |
计算
| $ \left\{ \begin{gathered} {i_b}\left( \varepsilon \right) = \left[ {I - \left( {2\varGamma + {U_d}} \right)/3R} \right]{e^{ - \frac{R}{{H - N}}\cdot \varepsilon }} + \left( {2\varGamma + {U_d}} \right)/3R ,\\ {i_c}\left( \varepsilon \right) = \left[ {\left( {2{U_d} - 2\varGamma } \right)/3R} \right]{e^{ - \frac{R}{{H - N}}\cdot \varepsilon }} - \left( {2{U_d} - 2\varGamma } \right)/3R。\\ \end{gathered} \right. $ | (11) |
通过求导
| $ {T_{em}} = \left( {p/\chi } \right) \times \left( {{e_a}{i_a} + {e_b}{i_b} + {e_c}{i_c}} \right) = - \left( {2/\chi } \right)p\varGamma \left( {{i_b} + {i_c}} \right)。$ | (12) |
在船用无刷直流电机AC/BC换相时,BC两相生成一个回路,此时ia电流下降,ib电流升高。Im表示电流换相初始电流,ia电流和时间关系为:
| $ {i_a} = \left[ { - \left( {{U_d} + 2E} \right)/3\left( {H - N} \right)} \right] + \left[ {{I_m} + \left( {\left( {{U_d} + 2E} \right)/3R} \right)} \right]{e^{\frac{t}{\kappa }}}。$ | (13) |
式中:
当ia电流降为0时,需要时间用t1描述,令ia=0,此时t1表达式如下:
| $ {t_1} = - \kappa \ln \left[ {\left( {{U_d} + 2E} \right)/\left( {{U_d} + 2E + 3R} \right){I_m}} \right]。$ | (14) |
ib电流升高至最大电流时间t2,t2表达式如下:
| $ {t_2} = - \kappa \ln \left[ {\left( {2{U_d} - 2E - 3R{I_m}} \right)/\left( {2{U_d} - 2E} \right)} \right] 。$ | (15) |
针对大型船用无刷直流电机是3种运行状态实施分析,采取合适开通角的大型船用无刷直流电机转矩脉动抑制方法。3种运行状态如下:
1)临界运行
在换相情况下,若t1=t2,大型船用无刷直流电机开通相电流升高量等于关闭相电流降低量,此时电机没有发生转矩脉动,表明电机为临界运行,此时转速为650 ~700 r/min,电流为18 ~20 A。
2)高速运行
若t1<t2,开通相电流升高量小于关闭相电流降低量,此时为抑制大型舰船用无刷直流电机转矩脉动,通过提前开通相开通时间的方式实现抑制。
| $ \begin{split} {t_\varsigma } = & \left( {{t_2} - {t_1}} \right)/2 = \\ & - 0.5\kappa \ln \frac{ {\left( {2{U_d} - E - 3R{I_m}} \right) \times \left( {{U_d} + 2E + 3R{I_m}} \right)}}{{\left( {2{U_d} - E} \right) \times \left( {{U_d} + E} \right)}}。\end{split} $ | (16) |
3)低速运行
若t1>t2,开通相电流升高量大于关闭相电流降低量,此时为抑制大型舰船用无刷直流电机转矩脉动,通过推迟开通相开通时间的方式实现抑制。
| $ \begin{split} {t_\tau } =& \left( {{t_1} - {t_2}} \right)/2 = \\ & - 0.5\kappa \ln \frac{{\left( {2{U_d} - E} \right) \times \left( {{U_d} + E} \right)}}{{\left( {{U_d} + E - 3R{I_m}} \right) \times \left( {2{U_d} - E + 3R{I_m}} \right)}} 。\end{split} $ | (17) |
当电角速度为
| $ \begin{split}{\alpha ^ * } = &- \frac{{\mu p{\text{π}} }}{{60}}\kappa \ln \left[ {\left( {2{U_d} - E - 3R{I_m}} \right)\left( {{U_d} + E + 3R{I_m}} \right)} \right]/\\ &\left[ {\left( {2{U_d} - E} \right)\left( {{U_d} + E} \right)} \right] 。\end{split}$ | (18) |
因
在大型舰船用无刷直流电机实际运行时,会受到漏磁的情况,需要导进1个修正系数
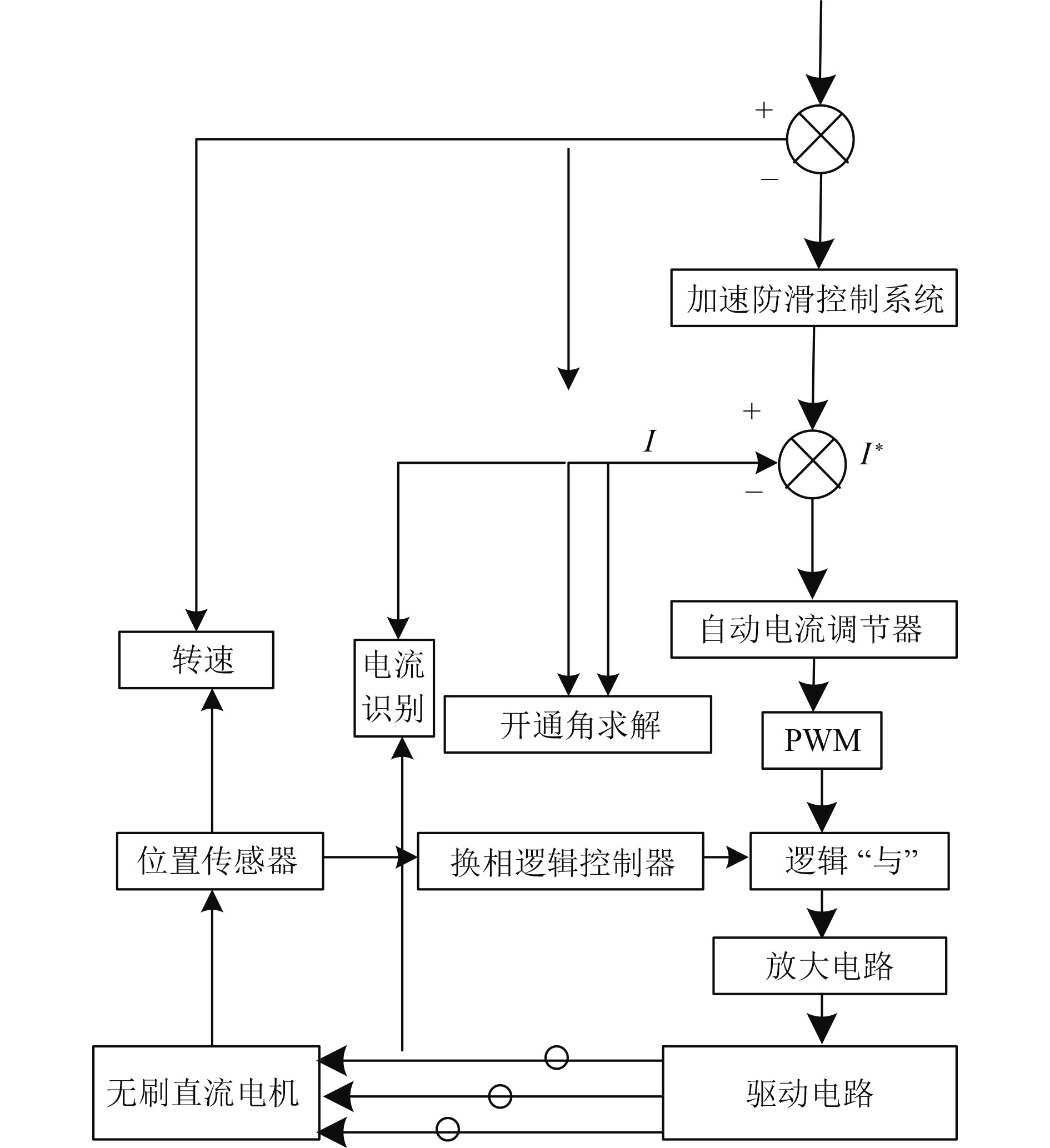
|
图 2 开通角的大型舰船用无刷直流电机控制模型 Fig. 2 Control model of brushless DC motor for largeships with open angle |
在Matlab/Simulin环境下测试本文方法的应用效果,将某海事部门的大型船用无刷直流电机作为试验对象。电机如表1所示。
|
|
表 1 电机参数 Tab.1 Test database |
电机低速和高速分别为400 r/min、1 500 r/min,在电机低速和高速运转的工况下,测试本文方法对大型船用无刷直流电机实施转矩脉动抑制的性能,得出转矩波动如图3所示。可知,在电机低速与高速运行的工况下,采用本文方法对大型船用无刷直流电机转矩脉动抑制的效果较好,本文方法可有效抑制电机转矩脉动,满足不同工况下电机运行的需求。
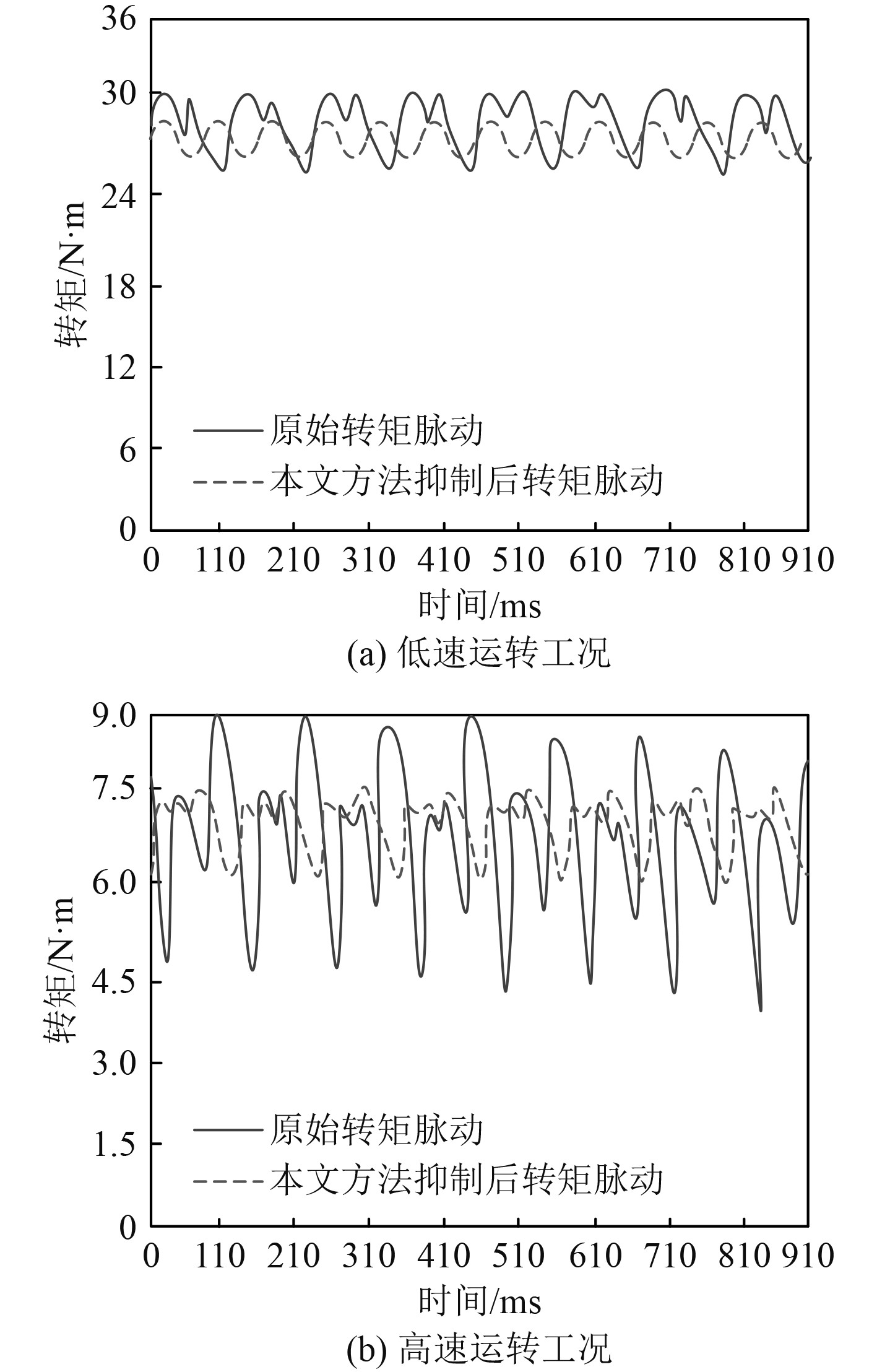
|
图 3 不同工况下转矩波动 Fig. 3 Torque fluctuation under different working conditions |
为了进一步验证本文方法的应用效果,分别采用本文方法、转子定向抑制方法[4],电压矢量的抑制方法[5],对大型船用无刷直流电机转矩脉动实施抑制,输出转矩脉动结果如图4所示。由图4(a)可知,采用文献转子定向抑制方法对大型舰船用无刷直流电机转矩脉动实施抑制,输出转矩脉动最高值大于35%,说明对抑制电机转矩脉动效果不佳。由图4(b)可知,采用电压矢量抑制方法对大型舰船用无刷直流电机转矩脉动实施抑制,输出转矩脉动最高值大于20%,说明对抑制电机转矩脉动效果一般。由图4(c)可知,采用本文方法对大型舰船用无刷直流电机转矩脉动实施抑制,输出转矩脉动最高值大于5%,说明本文方法的对电机转矩脉动抑制效果较好,符合电机转速运行的特点,保障大型舰船行驶的安全。

|
图 4 3种方法输出转矩脉动 Fig. 4 Three methods for outputting torque ripple |
为了提升电机转矩脉动抑制效率,设计了基于开通角的大型船用无刷直流电机转矩脉动抑制方法。实验结果表明,本文方法对电机转矩脉动效果抑制较好,提升了电机的稳定性。
| [1] |
姚绪梁, 赵继成, 王景芳, 等. 一种基于辅助升压前端的无刷直流电机换相转矩脉动抑制方法研究[J]. 中国电机工程学报, 2020, 40(9): 3021-3031. |
| [2] |
郭燚, 王超, 解文祥. 用于船舶永磁推进电机驱动控制的MMC模型预测方法[J]. 中国舰船研究, 2021, 16(4): 179. |
| [3] |
吕德刚, 张辰光, 侯征东. 无刷直流电机基于电流预测控制的转矩脉动抑制[J]. 哈尔滨理工大学学报, 2020, 25(5): 1-7. |
| [4] |
李珍国, 孙启航, 王鹏磊, 等. 基于转子永磁体磁场定向的无刷直流电机转矩脉动抑制[J]. 电工技术学报, 2020, 35(14): 2987-2996. |
| [5] |
陆可, 蔡广瀚, 向南辉, 等. 基于电压矢量注入的无刷直流电机换相转矩脉动抑制方法[J]. 中国电机工程学报, 2021, 41(10): 3592. |
| [6] |
何伟福, 王宁黎, 赵浩, 等. 基于峰谷互补方法的开关磁阻电机转矩脉动抑制研究[J]. 计量学报, 2021, 42(3): 352-357. |
 2023, Vol. 45
2023, Vol. 45
