柴油机作为船舶上的关键设备之一,燃油电磁阀在其控制系统中扮演着重要角色[1]。燃油电磁阀的故障会直接影响柴油机的正常运行[2],燃油电磁阀故障诊断方法逐渐向智能化方向发展[3]。在采集电磁阀的电流信号的基础上[4],通过提取信号的特征来实现故障诊断是常用的方法。小波包分解技术可以通过逐层分解高频和低频信号,提取更加细致和全面的信号特征[5]。
在现有的研究中,已有一些关于电磁阀故障诊断的方法。王钦惠等[6]通过对电磁阀信号进行小波分解和功率谱分析,实现了电磁阀开关故障状态的在轨实时诊断。张文啸等[7]构建基于变分自编码器的故障诊断模型,虽无需进行数据特征的提取,但模型结构对故障诊断效果的影响很大。
为解决上述问题,本文提出基于小波包分解的船用柴油机燃油电磁阀故障诊断方法。引入小波包分解方法,对电流信号进行分解,获取其多频带特征,能够更细致地提取信号的时频信息,从而更准确地描述电磁阀的工作状态和故障情况。
1 船用柴油机燃油电磁阀故障诊断 1.1 电磁阀特征提取船用柴油机燃油电磁阀故障信号具有非平稳性特点,小波变换是可实现非平稳信号时频分析的方法[8]。设定
小波包分解的变换函数描述为:
| $ {w_{n,j,k}}\left( k \right) = {2^{\frac{{ - j}}{2}}}{w_n}\left( {{2^{ - j}}t - k} \right) 。$ | (1) |
式中:
离散小波包变换可通过下式进行描述:
| $ \begin{gathered} {p_x}\left( {n,j,k} \right) = \left\langle {x\left( t \right),{w_{n,j,k}}\left( t \right)} \right\rangle \\ \int_{ - \infty }^{ + \infty } {x\left( t \right)\left[ {{2^{\frac{{ - j}}{2}}}w_n^*\left( {{2^{ - j}}t - k} \right)} \right]{\rm{d}}t} \\ \end{gathered} $ | (2) |
式中:x(t)为船用柴油机燃油电磁阀原始电流信号,
| $ \left\{ \begin{gathered} {p_x}\left( {2n,j,k} \right) = \sum\limits_{k \in z} {{h_{l - 2k}}{p_x}\left( {n,j - 1,l} \right)} ,\\ {p_x}\left( {2n + 1,j,k} \right) = \sum\limits_{l \in z} {{h_{l - 2k}}{p_x}\left( {n,j - 1,l} \right)}。\\ \end{gathered} \right. $ | (3) |
对各小波包分解系数作重构处理,以完成每个频带区间信号的获取,具体公式如下:
| $ \begin{gathered} {p_x}\left( {n,j,k} \right) = \\ \sum\limits_k {\left[ {{h_{k - 2l}}{p_x}\left( {2n,j + 1,k} \right) + {g_{k - 2l}}{p_x}\left( {2n + 1,j + 1,k} \right)} \right]}。\\ \end{gathered} $ | (4) |
在小波包变换过程中,每个频带的能量可通过下式进行计算:
| $ {E_{jk}}\left( i \right) = \sum\limits_k^n {{{\left| {{p_x}\left( {n,j,k} \right)} \right|}^2}}。$ | (5) |
对每个频带能量作归一化处理后,即可确定同一状态下,分解后各频带所含能量比例
| $ {e_{j,k}}\left( i \right) = \frac{{{E_{jk}}\left( i \right)}}{{\sum\limits_{i = 1}^{{2^k}} {{E_{jk}}\left( i \right)} }}。$ | (6) |
通过小波变换对船用柴油机燃油电磁阀的原始电流信号进行处理,提取出故障各频带的能量比例。
1.2 确定电磁阀电流信号敏感特征核主成分分析法(KPCA)的基本思想是利用非线性变换函数
将提取到的特征作为特征选择的输入,用
| $ C = \frac{{{e_{j,k}}\left( i \right)\sum\limits_{r = 1}^N {\psi \left( {{x_r}} \right)\psi {{\left( {{x_r}} \right)}^{\rm{T}}}} }}{N}\text{。} $ | (7) |
式中:
| $ \lambda = Cv。$ | (8) |
将
| $ {T_m} = {v^m}\psi \left( X \right) = \sum\limits_{r = 1}^N {\alpha _r^mK\left( {x,{x_r}} \right)} 。$ | (9) |
式中:
按由大到小顺序对
最小支持向量机(LSSVM)是建立在支持向量机(SVM)基础上的改进算法,采用自适应蚁群优化算法对参数进行寻优,以提高船用柴油机燃油电磁阀故障诊断精度。
1.3.1 电磁阀故障诊断模型将敏感特征计算结果输入电磁阀故障诊断模型,基于LSSVM的电磁阀故障诊断优化问题可描述为:
| $ \left\{ \begin{gathered} \min J\left( {w,\xi } \right) = \frac{{{{\left\| w \right\|}^2}}}{2} + {2^{ - 1}}c\sum\limits_{i = 1}^l {\xi _i^2} ,\\ {y_i}\left[ {{w^\varphi }\left( {{x_i}} \right) + b} \right] = 1 - \xi ,i = 1,2, \cdots l。\\ \end{gathered} \right. $ | (10) |
拉格朗日函数表达式为:
| $ \begin{array}{l}L\left(w,b\text{,}\xi \text{,}\delta \right)+\dfrac{{\Vert w\Vert }^{2}}{2}+{2}^{-1}c{\displaystyle \sum _{i=1}^{l}{\xi }_{i}^{2}}-\\ {\displaystyle \sum _{i=1}^{l}{\delta }_{i}}\left\{{y}_{i}\left[\phi \left({x}_{i}\right)w+b\right]-1+{\xi }_{i}\right\}。\end{array} $ | (11) |
式中:
| $ \left\{ \begin{gathered} \frac{{\partial L}}{{\partial w}} = 0 \to w = \sum\limits_{i = 1}^l {{\delta _i}\varphi \left( {{x_i}} \right)} ,\\ \frac{{\partial L}}{{\partial b}} = 0 \to \sum\limits_{i = 1}^l {\varphi \left( {{x_i}} \right) = 0} ,\\ \frac{{\partial L}}{{\partial {\xi _i}}} = 0 \to {\delta _i} = c{\xi _i},i = 1,2, \cdots ,l ,\\ \frac{{\partial L}}{{\partial \delta }} = 0 \to {y_i}\left[ {\varphi \left( {{x_i}} \right)w + b} \right] = 1 - {\xi _i}。\\ \end{gathered} \right. $ | (12) |
核函数表达式为:
| $ K\left( {{x_i},{x_j}} \right) = \varphi {\left( {{x_i}} \right)^{\rm{T}}}\varphi \left( {{x_j}} \right)。$ | (13) |
对式(12)进行处理,除去参数
| $ \left[ \begin{gathered} 0\mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} 1\mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \cdots \mathop {}\nolimits^{} \mathop {}\nolimits^{} 1 \\ 1\mathop {}\nolimits^{} K\left( {{x_1},{x_1} + {c^{ - 1}}} \right)\mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} K\left( {{x_1},{x_l}} \right) \\ \vdots \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\limits_{} \vdots \\ 1\mathop {}\nolimits^{} \mathop {}\nolimits^{} K\left( {{x_l},{x_1}} \right)\mathop {}\nolimits^{} \mathop {}\nolimits^{} K\left( {{x_1},{x_1} + {c^{ - 1}}} \right) \\ \end{gathered} \right]\left[ \begin{gathered} b \\ {\delta _1} \\ \vdots \\ {\delta _l} \\ \end{gathered} \right] = \left[ \begin{gathered} b \\ {y_1} \\ \vdots \\ {y_l} \\ \end{gathered} \right]。$ | (14) |
采用最小二乘法可确定参数
| $ y\left( x \right) = {\rm{sign}}\left[ {\sum\limits_{i = 1}^l {{\delta _i}K\left( {x,{x_i}} \right) + b} } \right]。$ | (15) |
选用径向基核函数,其计算公式为:
| $ K\left( {{x_i},{x_j}} \right) = \exp \left( {\frac{{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{{\sigma ^2}}}} \right)。$ | (16) |
式中,
为提高船用柴油机燃油电磁阀故障诊断效果,采用自适应蚁群算法对故障诊断模型参数
船用柴油机燃油电磁阀故障诊断模型参数优化的状态转移规则通过下式进行描述:
| $ P\left( {\tau _j^k\left( {{I_{pi}}} \right)} \right) = \left\{ \begin{gathered} \arg \mathop {}\nolimits^{} \max \left( \tau \right),f < {F_0}\left( t \right),\\ {S_{rand}}\mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} ,{\rm{else}}。\\ \end{gathered} \right. $ | (17) |
| $ {F_0}\left( t \right) = \min \left( {1 - {e^{ - \varepsilon t}},{F_{\max }}} \right)。$ | (18) |
式中,参数
全部蚂蚁均完成参数选择后,对其做迭代训练,确定输出误差,并保存各优化参数的最优值。信息素调整公式描述为:
| $ \left\{ \begin{gathered} \tau _j^{}\left( {{I_{pi}}} \right)\left( {t + m} \right) = \left( {1 - \rho \left( t \right)} \right)\tau _j^{}\left( {{I_{pi}}} \right)\left( t \right) + \Delta \tau _j^{}\left( {{I_{pi}}} \right),\\ \Delta \tau _j^{}\left( {{I_{pi}}} \right) = \sum\limits_{k = 1}^s {\Delta \tau _j^k\left( {{I_{pi}}} \right)},\\ \rho \left( t \right) = \max \left( {\mu p\left( {t - 1} \right),{\rho _{\min }}} \right)。\\ \end{gathered} \right. $ | (19) |
式中:
结合基于LSSVM的电磁阀故障诊断模型和自适应蚁群算法,通过调整算法中的挥发因子、状态转移规则和信息素等,实现LSSVM模型中的参数优化。
2 实验分析以某船用柴油机燃油电磁阀作为实验对象,通过Python采集电磁阀原始电流信号,并进行处理。构建实验样本数据集,数据总量为5000,其中正常信号样本3800个,故障样本为1200个,对应弹簧断裂、阀芯轻微卡顿、阀芯卡死、线圈断路、二极管击穿短路5种不同运行工况。通过Scikit-learn训练电磁阀故障诊断模型,完成参数优化。优化后的参数:学习率为0.01;正则化参数为0.001;迭代次数为1000;批处理大小为64;隐藏层节点数为128;模型的深度为2。将本文方法应用到船用柴油机燃油电磁阀故障诊断中,分析其诊断性能。
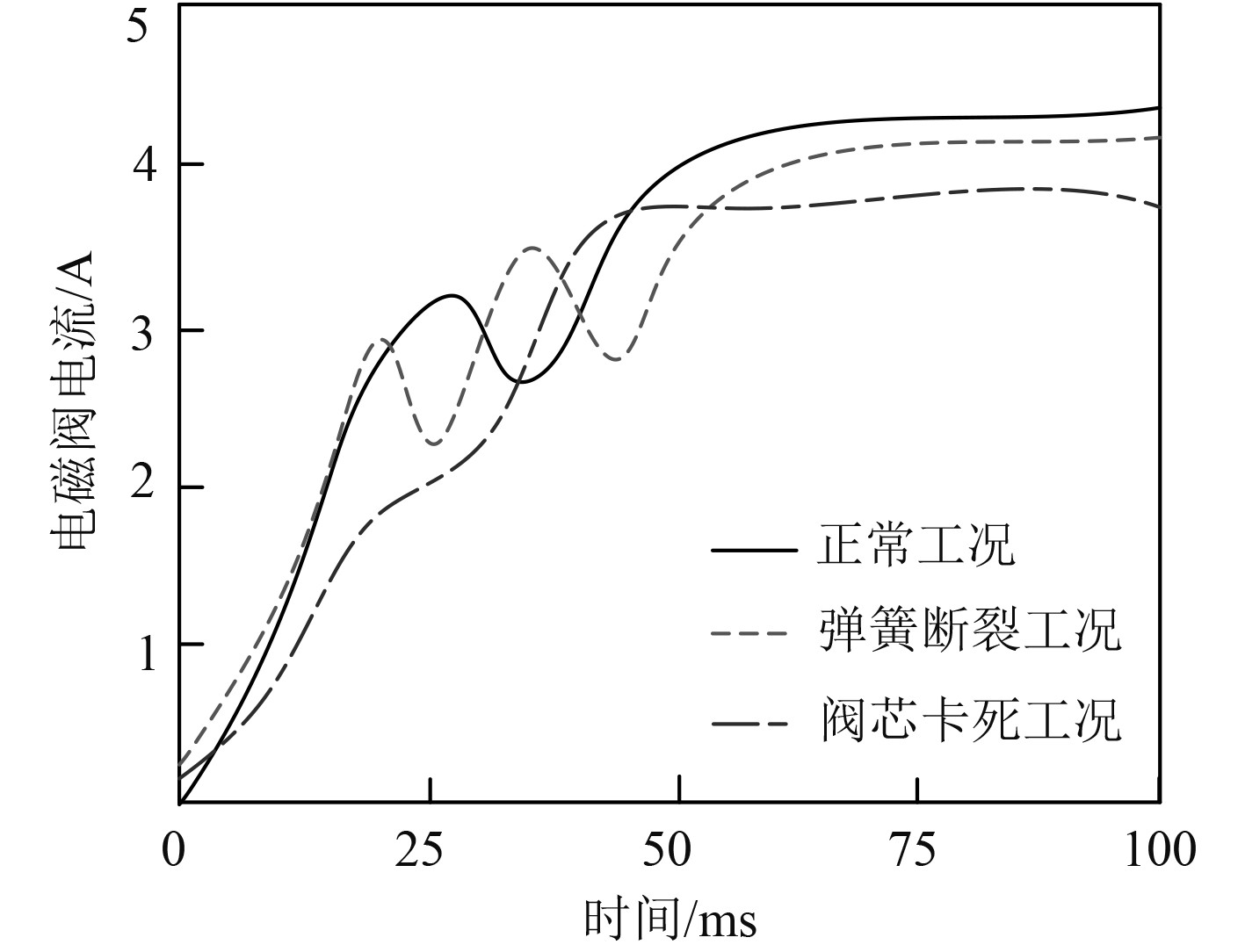
以船用柴油机燃油电磁阀弹簧断裂、阀芯卡死2种故障工况为例,采集2种工况下的船用柴油机燃油电磁阀电流信号,并与正常运行工况下的电流信号进行对比,分析不同运行工况下的电磁阀电流信号差异,实验结果如图1所示。
|
图 1 不同运行工况下电磁阀电流信号差异分析 Fig. 1 Analysis of current signal differences of electromagnetic valves under different operating conditions |
分析可知,船用柴油机燃油电磁阀故障会对其电流信号特征产生影响,将电磁阀电流信号作为其故障诊断依据可行。
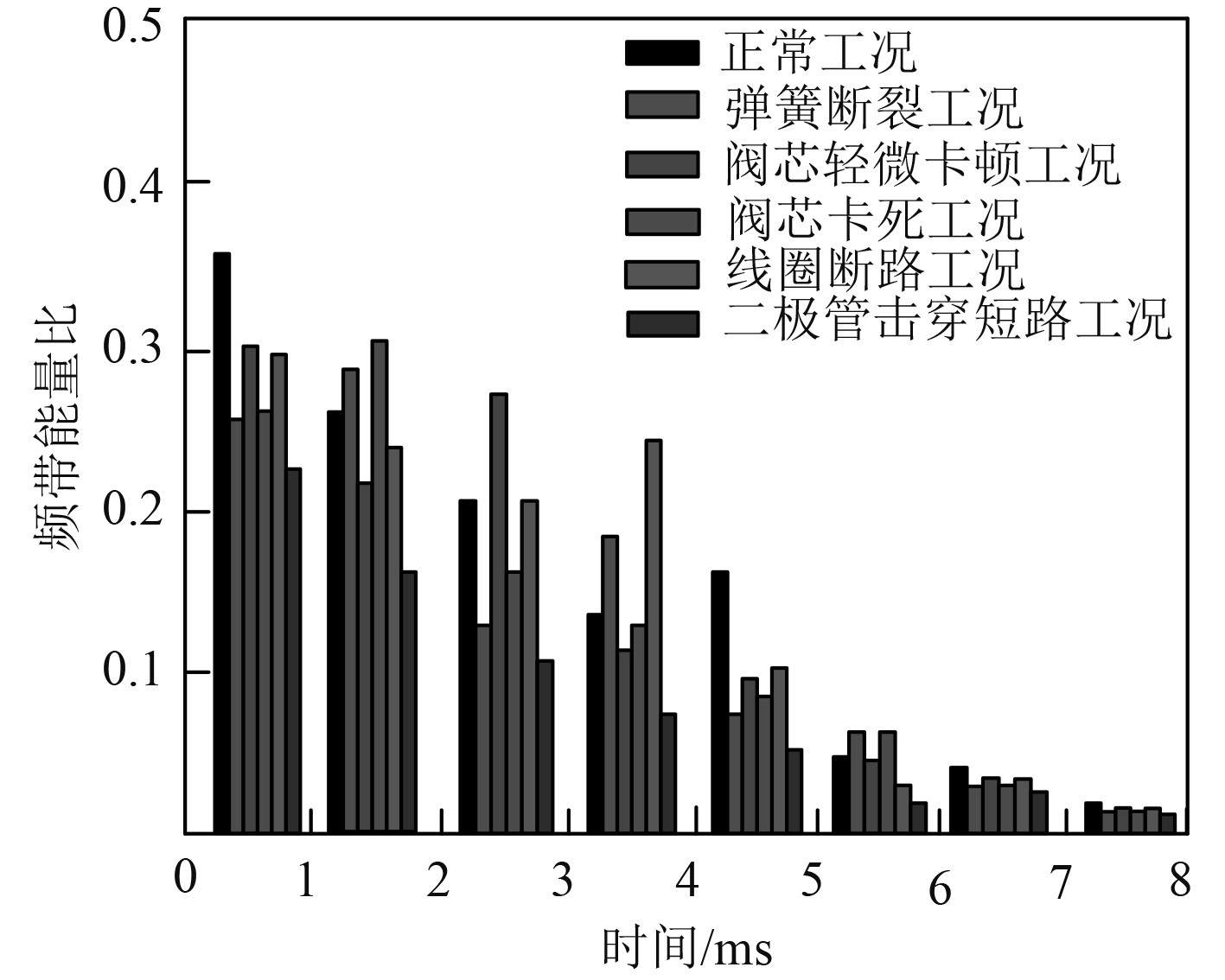
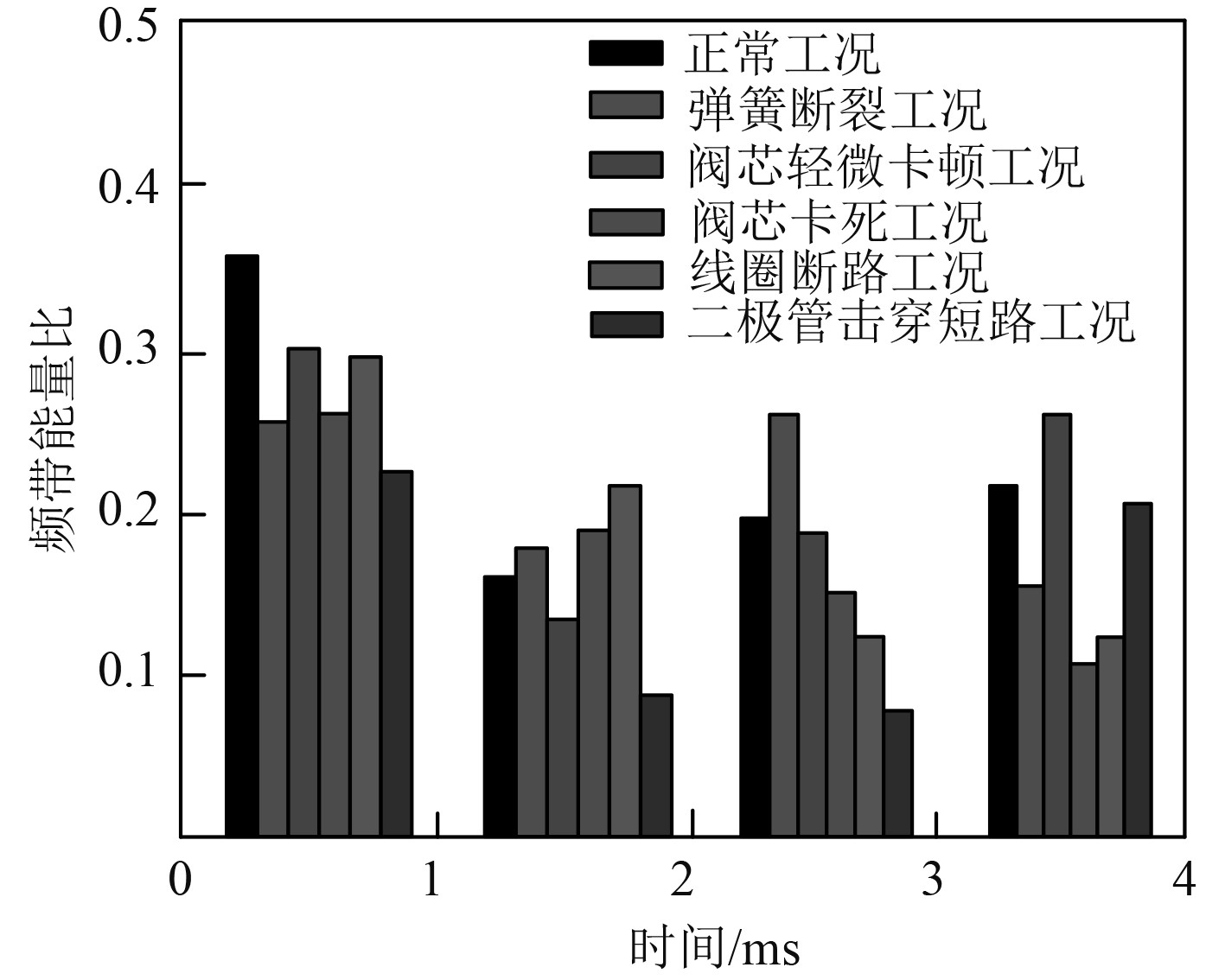
采用本文方法对不同工况下的电磁阀电流信号进行分解,并与小波分析结果进行对比,通过分析不同频带能量比值差异验证本文方法的电流信号分解性能,实验结果如图2和图3所示。
|
图 2 本文方法分解结果分析 Fig. 2 Analysis of the decomposition results of the method in this article |
|
图 3 小波分解结果分析 Fig. 3 Analysis of wavelet decomposition results |
分析可知,本文方法具有突出的信号特征提取能力。
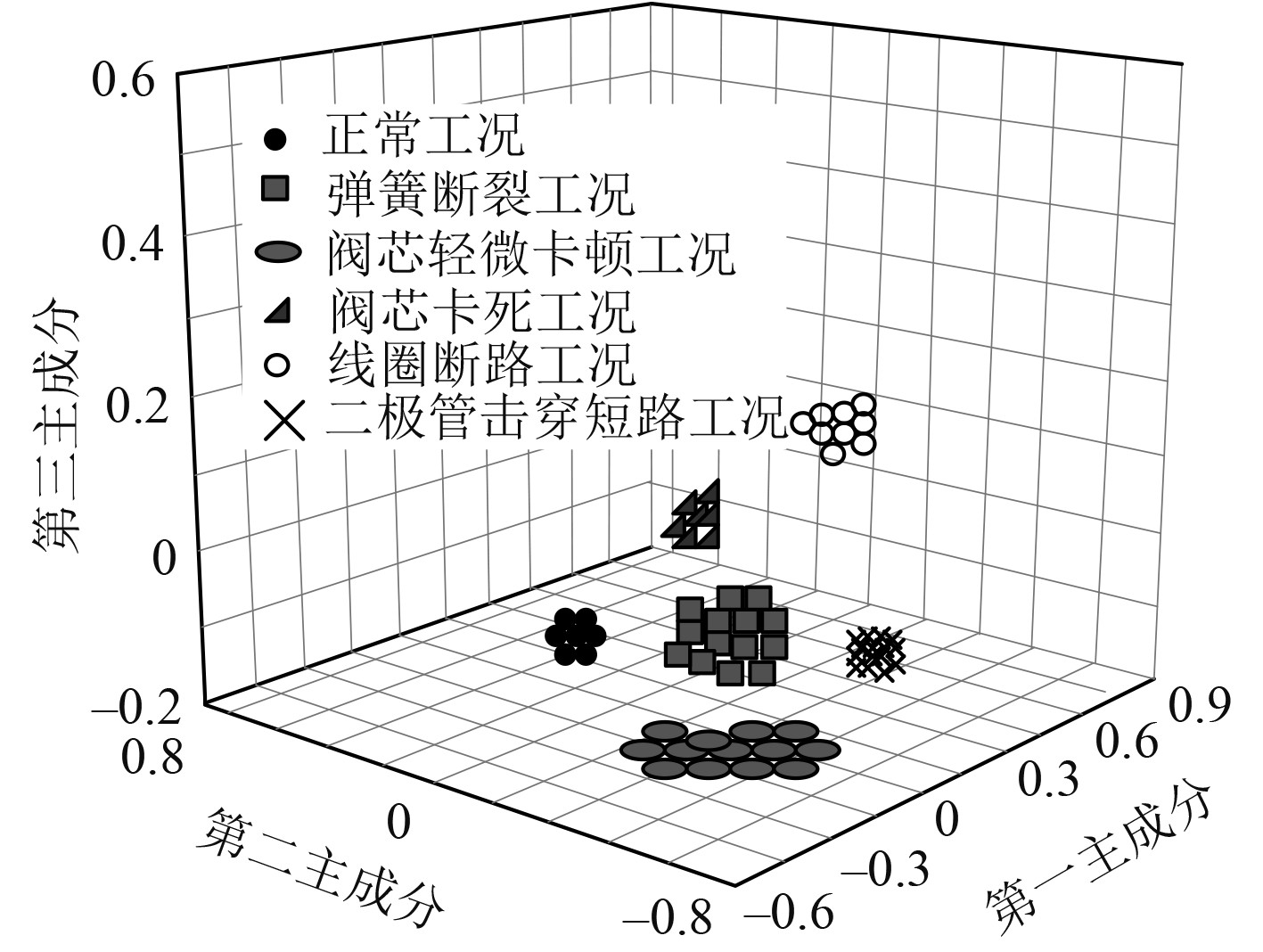
通过对比分析不同工况电磁阀故障识别效果,验证本文方法的有效性,实验结果如图4和图5所示。
|
图 4 本文方法故障识别结果分析 Fig. 4 Analysis of fault identification results of the method in this article |
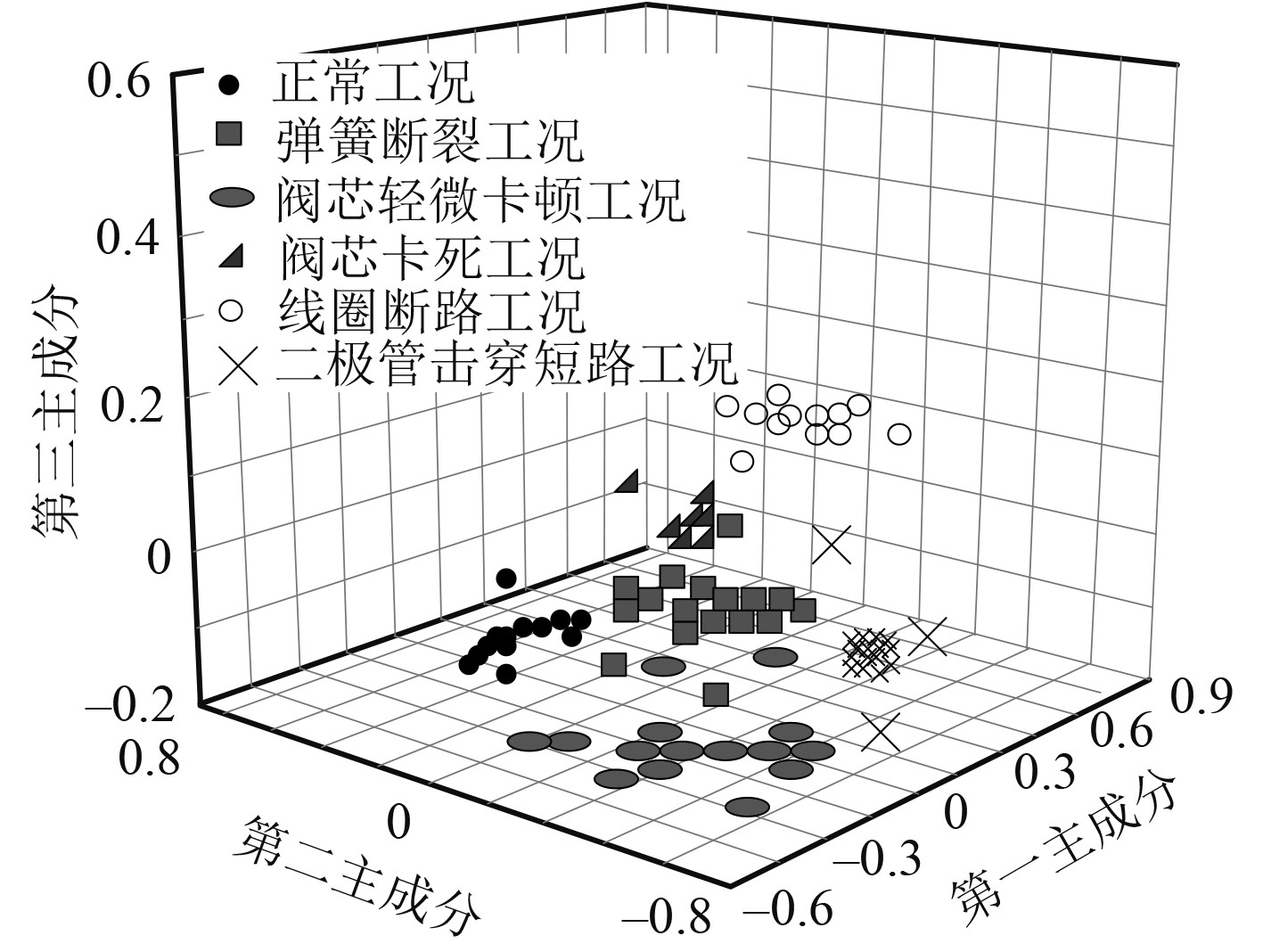
|
图 5 小波分析+KPCA降维后的故障识别结果分析 Fig. 5 Analysis of Fault Identification Results after Wavelet Analysis and KPCA Dimension Reduction |
分析可知,本文方法具有突出的故障辨识能力。
3 结 语1)故障工况下的电流特性曲线与正常工况存在差异。
2)本文方法提取的电磁阀原始电流信号特征更精细,不同运行工况信号特征差异高;特征降维有利于电磁阀故障效果的提升。
3)本文方法可实现电磁阀故障诊断,诊断效果突出。
| [1] |
黄烨鑫, 万振刚, 程琛. 基于改进鲸鱼算法寻优SVM的船用柴油机燃油系统故障诊断方法研究[J]. 计算技术与自动化, 2021, 40(2): 53-56. |
| [2] |
谢海龙, 陈国顺, 谢海勇, 等. 电磁阀常见故障的分析及处理[J]. 阀门, 2020, 230(4): 47-50. |
| [3] |
张明兴. 发动机OCV电磁阀卡滞问题解析[J]. 汽车制造业, 2022, 677(1): 39-41. |
| [4] |
马栋, 刘志浩, 高钦和, 等. 基于多特征融合的电磁换向阀故障模式识别[J]. 北京航空航天大学学报, 2023, 49(4): 913-921. |
| [5] |
郝德琛, 李华玲, 黄晋英. 小波包分解和改进ResNet行星齿轮箱故障诊断方法[J]. 传感器与微系统, 2022, 41(8): 116. |
| [6] |
王钦惠, 胡向宇, 崔梧玉, 等. 基于小波分析的电磁阀在轨实时诊断[J]. 真空与低温, 2021, 27(3): 292-295. |
| [7] |
张文啸, 孟国香, 叶骞. 基于Triplet loss的电磁阀故障识别方法[J]. 液压与气动, 2022, 46(9): 116-125. |
| [8] |
朱兴统. 基于小波包分解和K最近邻算法的轴承故障诊断方法[J]. 装备制造技术, 2020, 302(2): 24. |
 2023, Vol. 45
2023, Vol. 45
