2. 中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;
3. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169
2. The State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China;
3. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China
随着海洋技术与装备水平的突飞猛进,以自主水下机器人(Autonomous Underwater Vehicle, AUV)为代表的新型海洋无人智能装备在海洋科考和勘探领域得到了广泛应用[1]。其中,重量在10 kg以下的微型自主水下机器人是一种在近几年新出现的自主水下机器人产品。因其耐压舱内部空间有限、搭载的电池能量密度有限等原因,微型AUV的水下航程一般较短。对于微型AUV这一瓶颈问题,可采用减少天线等突出物方法,以降低微型AUV的水下航行阻力,提高其续航能力[2]。通过这一方法还可减少天线导致的AUV尾部流场不稳定等问题,从而降低AUV的航行噪声,提高推进器工作效率[3]。
针对以上问题,严天宏等[4]基于曲柄摇杆和双摇杆机构提出了2种天线折叠机构设计方案,通过舵机驱动连杆实现天线部件的升起与折叠。郑志航等[2]基于丝杆-滑轨机构设计了一种天线折叠机构,通过电机带动丝杆转动实现天线的升起与折叠。宫颖博等[5]基于齿轮-齿条机构设计了一种天线升降机构,通过电机驱动齿轮实现天线的升起与缩回。以上3种方案的机构在处于折叠或缩回状态时,天线完全处于舱段内部,消除了天线部件的水下航行阻力。但以上方案应用在微型AUV上存在以下问题:1)天线部件尺寸受到微型AUV的舱段长度或直径的限制,导致天线升起后的高度有限,进而影响AUV的通信与定位质量;2)对耐压舱段内部空间占用过大,应用在微型AUV上会严重降低内部空间的利用率;3)相关机构质量均集中在舱段上部,对微型AUV的衡重设计产生较大影响[6]。
可见,对于微型AUV来说,一方面常规设计类型的天线部件对其航行阻力及运动操纵性影响尤为明显,另一方面微型AUV的外形尺寸限制导致了已有折叠天线的技术方案均不适用。因此本文提出一种可适用于微型AUV的折叠天线技术方案,该方案在保证水面航行通信及定位质量同时,可有效减少AUV的水下航行阻力。
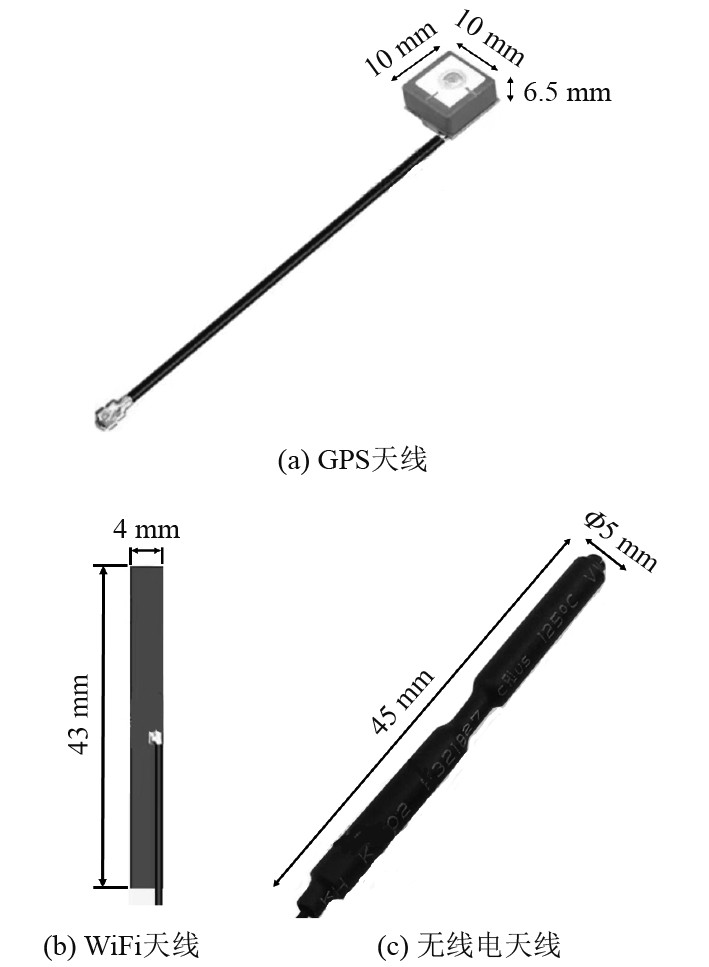
1 天线外形设计与分析 1.1 外形设计本文设计的折叠天线将安装在直径为76.2 mm、长度为932 mm的微型AUV载体上。为满足微型AUV的水面卫星定位、近距离高速数据传输和远距离无线通信功能,选用如图1所示的GPS、WiFi和无线电天线产品,并将其集成到折叠天线的天线部件中。其中GPS天线的尺寸为10 mm×10 mm×6.5 mm;WiFi贴片式天线的尺寸为43 mm×4 mm;无线电天线尺寸为Φ5 mm×45 mm。
|
图 1 GPS、WiFi和无线电天线实物图 Fig. 1 GPS, WiFi and radio antennas |
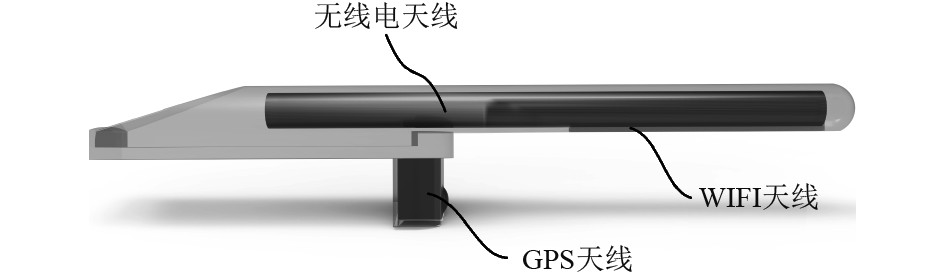
集成了GPS、WiFi和无线电天线的折叠天线部件如图2所示,其尺寸为122 mm×13.9 mm×14.39 mm。搭载该天线部件的微型AUV如图3所示。
|
图 2 天线部件 Fig. 2 The antenna |

|
图 3 微型AUV模型图 Fig. 3 The micro AUV models |
计算图3所示的2个微型AUV模型在0.5~3.5 m/s航速下的水下航行阻力,验证天线部件处于折叠状态时的减阻效果。
以模型1为例,在SolidWorks中获取截面尺寸如图4(a)所示的长方体计算域。为尽可能减小计算域边界对流体的影响,设AUV总长为L,计算域入口边界距AUV首部距离L,出口边界距AUV尾部距离2L,四周边界距AUV距离L;边界类型设置如图4(b)所示。入口边界设定为速度入口(velocity inlet),出口边界及四周边界皆设置为压力出口(pressure outlet),压力值为1个标准大气压。

|
图 4 计算域尺寸与边界类型设置 Fig. 4 Computational domain size and boundary type settings |
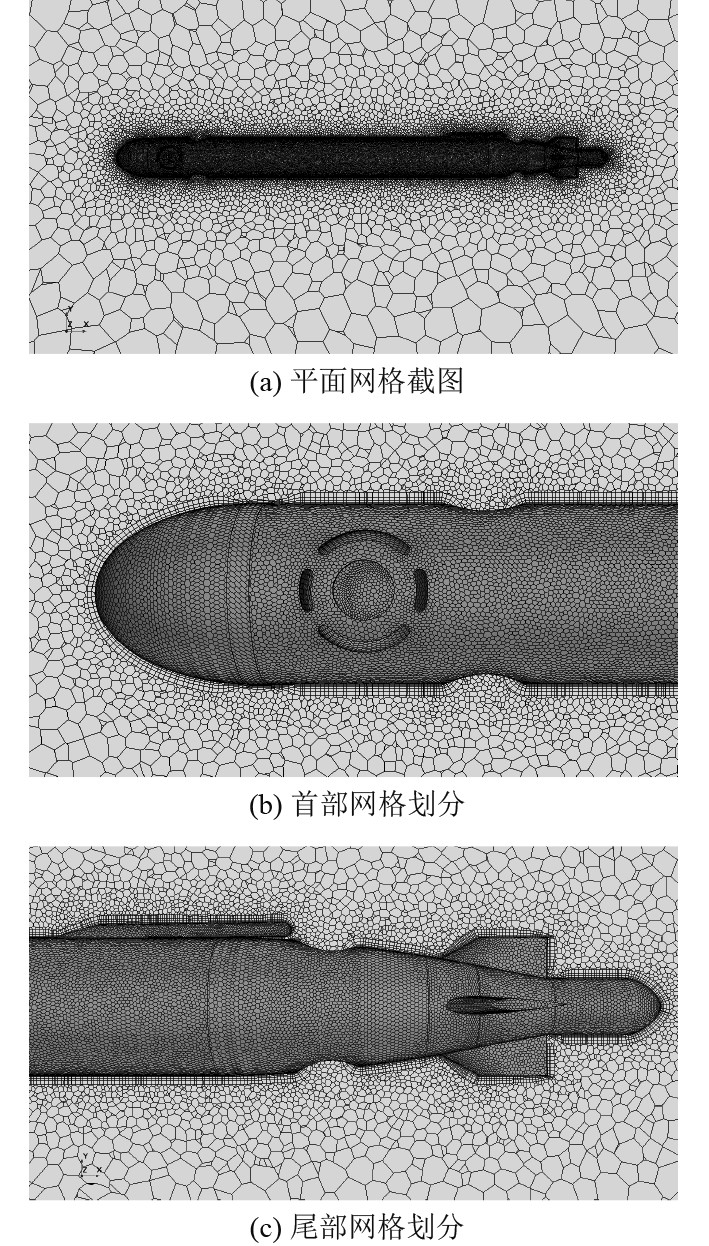
将计算域模型导入到STAR-CCM+中进行计算,使用多面体网格生成器[7]对计算域进行网格离散。之后进行网格控制,如局部网格加密,调节棱柱层数、总厚度和生成速率等。生成的网格总节点数约为316万,网络生成示意图如图5所示。
|
图 5 网格生成示意图 Fig. 5 Schematic diagram of grid generation |
湍流模型选择剪切应力传输K-Omega,简称SSTK-Omega模型[8],该模型可较好预测近壁面区域和远场的流体运动状态。阻力计算结果如表1所示。
|
|
表 1 模型1航行阻力数据 Tab.1 Navigation resistance data of models one |
为验证该仿真计算结果准确性,使用经验公式[9]计算模型1的航行阻力:
| $ {R}_{T}=\frac{1}{2}\rho {\text{V}}^{2}·S({C}_{f}+△{C}_{f}+{C}_{PV}+{C}_{AP}) 。$ | (1) |
式中:
将海水密度
|
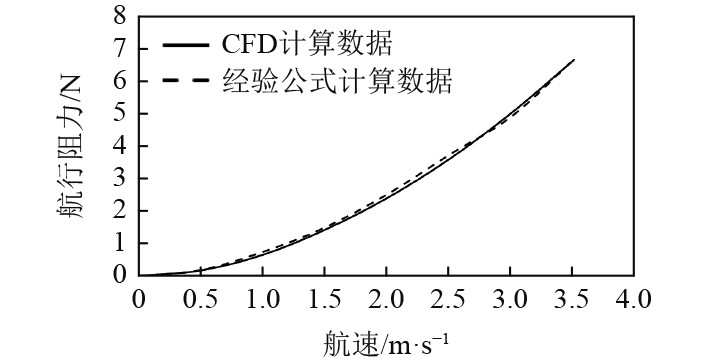
图 6 经验公式计算与CFD计算结果对比图 Fig. 6 Comparison of empirical formula calculation and CFD calculation results |
可看出,使用STAR-CCM+计算结果与经验公式计算结果几乎一致,2组数据的相关系数为0.95,故可认为上述仿真是准确的。使用相同方法计算模型2的航行阻力,结果如表2所示。图7与图8分别为模型1和模型2航速为0.5 m/s时的压力云图和速度云图。
|
|
表 2 不同模型航行阻力数据 Tab.2 Navigation resistance data of different models |
|
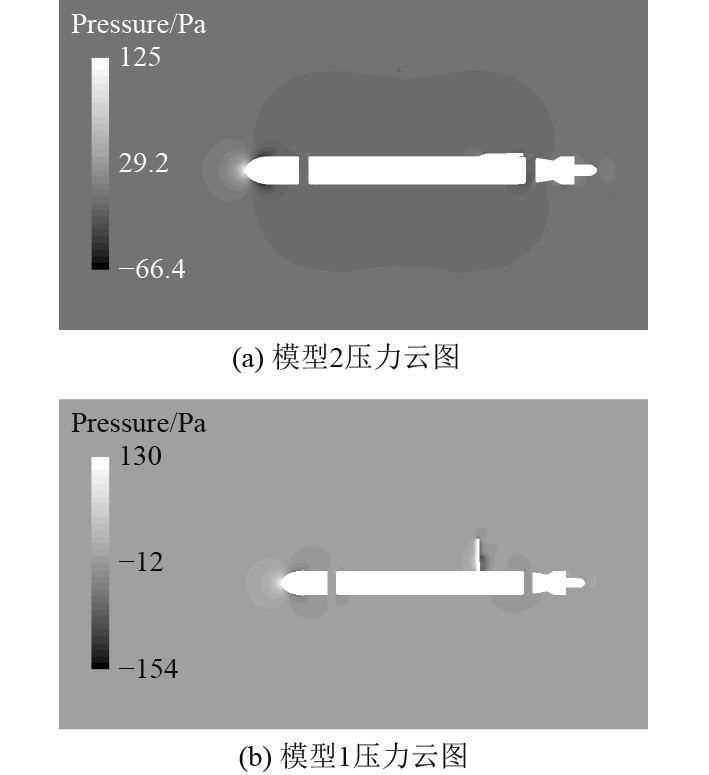
图 7 2个模型的压力云图 Fig. 7 Pressure contours of the two models |

|
图 8 2个模型的速度云图 Fig. 8 Velocity contours of the two models |
通过分析表2数据与图7所示的压力云图,可知微型AUV在水下航行时,天线处于折叠状态相比于天线处于直立状态航行阻力更小,前者相对后者最高可减少50.40%、最低可减少34.26%、平均可减少40.19%的航行阻力。此外,通过分析速度云图可看出,天线处于折叠状态下天线部件对微型AUV周边流场影响更小。
2 折叠机构设计与分析 2.1 机构设计按照天线升起与折叠状态下的对应位置使用解析法设计四连杆机构[10],以实现天线的折叠与升起。
图9为铰链四连杆机构示意图。图中,两连架杆对应角位置为

|
图 9 铰链四连杆机构示意图 Fig. 9 Schematic diagram of hinge four-bar linkage |
| $ \cos (\phi + {\phi _0}) = {P_0}\cos (\psi + {\psi _0}) + {P_1}\cos [(\psi + {\psi _0}) - (\phi + {\phi _0})] + {P_2} 。$ | (2) |
式中:
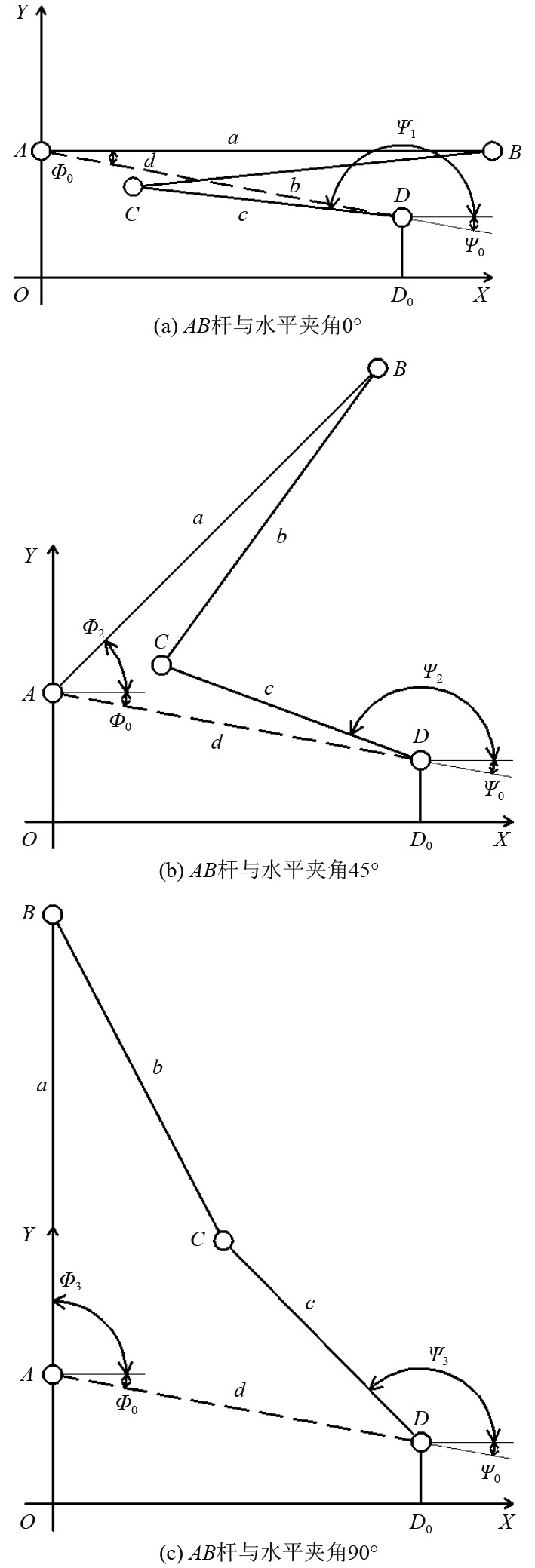
如图10所示,取
|
图 10 AB杆3种不同角度状态下连杆示意图 Fig. 10 Schematic diagram of connecting rod under three different angles of AB rod |
| $ \left\{ \begin{aligned} \cos ({\phi _1} + {\phi _0}) =&{P_0}\cos ({\psi _1} + {\psi _0}) + \\& {P_1}\cos [({\psi _1} + {\psi _0}) - ({\phi _1} + {\phi _0})] + {P_2},\\ \cos ({\phi _2} + {\phi _0}) =& {P_0}\cos ({\psi _2} + {\psi _0}) + \\& {P_1}\cos [({\psi _2} + {\psi _0}) - ({\phi _2} + {\phi _0})] + {P_2},\\ \cos ({\phi _3} + {\phi _0}) =& {P_0}\cos ({\psi _3} + {\psi _0}) + \\& {P_1}\cos [({\psi _3} + {\psi _0}) - ({\phi _3} + {\phi _0})] + {P_2} 。\end{aligned} \right.$ | (3) |
综合考虑微型AUV外形尺寸、零部件的安装方式和折叠机构的传动机构设计等设计因素,机架
| $ {P}_{0}=0.59987,{P}_{1}=-0.73767,{P}_{2}=0.81319,$ | (4) |
| $ m=0.799\;58,n=0.599\;87,l=0.813\;19 。$ | (5) |
由

|
图 11 折叠机构模型图 Fig. 11 Model diagram of the folding mechanism |
折叠天线机构使用舵机驱动,其驱动机构位于舱段耐压舱内部,与折叠机构通过一组锥齿轮啮合传动。驱动机构中使用一组齿数比为1∶2的直齿轮实现减速增矩,且通过在传动轴上布置2个封闭圈实现传动轴的动密封,驱动机构的结构图如图12所示。

|
图 12 驱动机构结构图 Fig. 12 Drive mechanism diagram |
如图13所示,将天线部件安装到天线支架上后,使用SolidWorks三维建模软件在各零部件间添加配合关系,运行Motion组件进行初步运动仿真,完成一个仿真流程后选择将模型输出到Adams仿真软件,在Adams中进行机构的运动学与动力学仿真。

|
图 13 折叠天线机构模型图 Fig. 13 Model diagram of folded antenna mechanism |
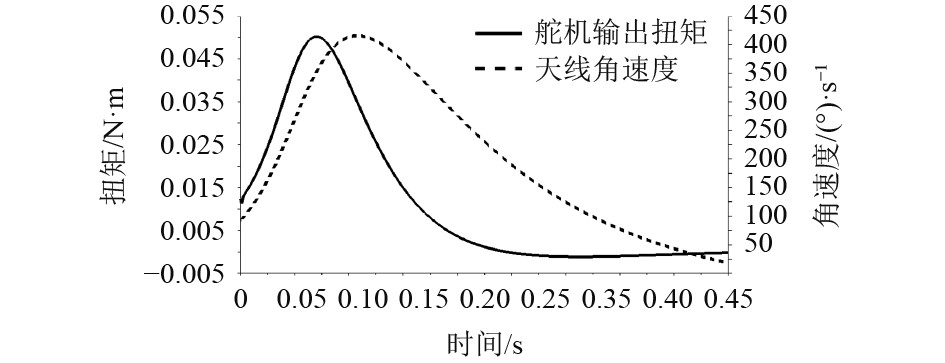
首先对主动件即舵机所连小齿轮添加旋转副驱动来模拟舵机的转动,其角速度设定为200°/s。其次根据在样机中拟使用的材料对各零件设置材料密度。最后对相互接触的零部件根据相对运动关系,添加摩擦系数:静摩擦系数设置为0.5,动摩擦系数设置为0.3。前置条件设定完成之后运行仿真,提取舵机输出扭矩曲线和天线升起时的角速度幅值曲线,其结果如图14所示。
|
图 14 舵机输出扭矩曲线和天线角速度幅值曲线 Fig. 14 Servo output torque curve and antenna angular velocity amplitude curve |
可知,天线升起过程中所需舵机最大输出扭矩为0.05 N·m,小于微型水下机器人所选舵机(KST-X08H)在200°/s下的额定扭矩(0.14 N·m),可知舵机满足使用要求。天线机构的运动范围为0°~90°,符合设计要求,能够覆盖从水平折叠到竖直升起的整个微型AUV所需要的运动范围。从天线升起时的角速度幅值曲线可以看出,当机构运行0.11 s天线升起到38.5°时天线角速度达到最大值约400°/s,之后天线继续升起角速度缓慢减低,直到天线完全升起同时角速度降为0°/s,整个过程用时约0.5 s。该过程角速度过渡比较平稳,不会对驱动系统造成冲击,能实现折叠天线机构的稳定运行。
3 样机试验验证 3.1 折叠机构功能测试为验证折叠天线机构是否可正常运转,在原理样机上进行天线结构升起与折叠测试。完成样机的各零部件装配后控制舵机运转,如图15所示,折叠天线机构可正常运行,其中升起用时不到1 s,与仿真结果相近,但最大升起角度仅有75°。通过观察得知,导致这一结果的主要原因在于WIFI、无线电和GPS天线灌封安装到天线支架上后,天线与耐压舱内部通信设备相连接的线缆弹性较强,给天线升起带来了额外的阻力距,导致天线无法升起至预定角度。经后续测试天线最大升起角度为75°不影响微型AUV的水面航行通信功能,后续考虑通过使用线材较软的天线导线来解决这一问题。

|
图 15 折叠天线升降试验 Fig. 15 The folding antenna lift test |
为了验证该折叠天线机构中WIFI、无线电和GPS等天线接收信号的稳定性,使用如图16所示的微型AUV原理样机开展水面航行和水下航行相关试验。

|
图 16 微型AUV原理样机 Fig. 16 Micro AUV prototype |
水面航行状态下,通过控制折叠机构保持天线处于升起状态。试验结果表明,WIFI与无线电信号良好,满足水面数据传输要求。GPS在水面航行过程中可稳定获取卫星定位信号,通过获取GPS定位数据得到的微型AUV水面航行轨迹如图17所示。

|
图 17 AUV航行轨迹 Fig. 17 AUV navigation track |
水下定深和定向航行状态下,使天线处于折叠状态,将目标航向角设定为325°,目标深度设为2 m,试验数据如图18所示。从图18(a)看出,天线机构折叠状态下微型AUV可在水下航行时保持较好航向,航向稳定后其误差不大于±2°。从图18(b)可知,微型AUV具备定深的调节能力,定深航行误差不大于±0.5 m,后续可继续优化相关控制参数,以进一步提高微型AUV的水下自主航行能力。

|
图 18 AUV定深定向试验结果 Fig. 18 The results of the AUV fixed depth and orientation test |
本文设计了一型用于微型自主水下机器人的折叠天线机构,其机构简单可靠,天线部件尺寸不受限于天线舱段直径或长度,弥补了现有升降、折叠天线机构不适用于微型AUV的不足。通过仿真与试验验证了设计方案的可靠性,具体结论如下:
1)设计的折叠天线具有水面卫星定位、近距离高速数据传输和远距离无线通信功能。
2)通过CFD仿真计算了不同航速下的微型AUV航行阻力,结果表明天线处于折叠状态相比于天线处于直立状态可减少不少于34.26%的航行阻力。
3)通过对折叠天线机构进行运动学与动力学仿真,天线部件运动范围为0°~90°,满足了微型AUV的使用需求;舵机最大输出扭矩为0.05 N·m,小于所选舵机的额定扭矩。
4)通过在原理样机上试验,验证了折叠机构可正常运转;通过湖上试验,一方面验证了天线处于升起状态时接收WiFi、无线电和GPS信号的稳定性,另一方面验证了天线处于折叠状态时,微型AUV的水下定向、定深航行功能。
在后续的研究中,一方面需对折叠天线的天线外形进行优化设计,以进一步减少微型AUV的航行阻力;另一方面要加工铝合金壳体的微型AUV样机,提高微型AUV的耐压能力和水下航行功能的可靠性。
| [1] |
ALAAELDEEN M, DUAN W Y. Overview on the development of autonomous underwater vehicles(AUVs)[J]. Journal of Ship Mechanics, 2016.
|
| [2] |
郑志航, 严天宏, 何波, 等. 一种长航程AUV折叠天线机构与密封设计[J]. 舰船科学技术, 2021, 43(9): 4. ZHENG Z H, YAN T H, HE B, et al. The mechanism and sealing design of a long-range AUV folding antenna[J]. Ship Science and Technology, 2021, 43(9): 4. |
| [3] |
MA Yuanliang, ZHANG Qunfei, ZHANG Honglei. 6G: Ubiquitously extending to the vast underwater world of the oceans[J]. Engineering, 2022, 8(1): 12-17. |
| [4] |
严天宏, 申洪彬, 何波, 等. 自主水下航行器折叠天线设计[J]. 机械设计与制造, 2021. YAN T H, SHEN H B, HE B, et al. Design of folding antenna for autonomous underwater vehicle[J]. Machinery Design & Manufacture, 2021. |
| [5] |
宫颖博, 严天宏, 何波. 一种自主水下航行器用可伸缩天线装置[P]. CN111478012A, 2020.
|
| [6] |
秦玉峰. 小型长航程AUV结构设计及动力学分析[D]. 北京: 国家海洋技术中心, 2017.
|
| [7] |
詹成胜, 刘祖源, 程细得. 潜艇水动力系数数值计算[J]. 船海工程, 2008(3): 1-4. ZHAN D S, LIU Z Y, CHENG X D. Numerical calculation of the submarineʾs hydrodynamic coefficients[J]. Ship & Ocean Engineering, 2008(3): 1-4. |
| [8] |
高婷, 庞永杰, 王亚兴, 等. 水下航行器水动力系数计算方法[J]. 哈尔滨工程大学学报, 2019, 40(1): 174-180. GAO T, PANG Y G, WANG Y X, et al. Calculation method of hydrodynamic coefficients for underwater vehicles[J]. Journal of Harbin Engineering University, 2019, 40(1): 174-180. |
| [9] |
张铁栋. 潜水器设计原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011: 117–120.
|
| [10] |
孙恒, 陈作模, 葛文杰, 等. 机械原理(第八版)[M]. 北京: 高等教育出版社, 2013: 124–150.
|
 2023, Vol. 45
2023, Vol. 45
