2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 辽宁省水下机器人重点实验室,辽宁 沈阳 110169;
4. 中国科学院大学,北京 100049
2. Institute for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. Key Laboratory of Marine Robotics, Shenyang 110169, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
AUV因其自主、智能的特性,在水下环境探测和资源勘探方面发挥了人工无法比拟的作用[1]。AUV作业过程中,受到海浪和水流的干扰,所以在近海底自主观测、轨迹跟踪等要求精细控制的场景,必须考虑外界环境扰动对AUV稳定性的影响。AUV平台具有多变量、非线性、强耦合、外界干扰多和内部参数时变的特点,要想达到理想的控制效果,往往需要收敛速度快、抗干扰、鲁棒能力强的控制器,这些要求给控制系统的设计带来了很多困难。
基于对象信息的现代控制理论包含对模型不确定性的近似,这种近似性使得AUV控制系统性能有待提高。针对控制器本身存在不足及其对扰动抑制能力弱的问题,韩京清等[3-5]提出了一种抗扰动控制方法,对控制模型信息依赖少,具有天然的解耦性和优秀的抗干扰能力,被广泛应用于机器人控制。针对非线性自抗扰控制参数比较多的问题,高志强[6]提出了线性化版本,简化了工程实现和参数整定,更加便于工业推广。
目前针对线性自抗扰控制器的理论研究主要集中在其时域和频域特性的探索,以及与PID的关系的证明上,总结出了很多控制器调参的指导方法。其中,JIN等[7]证明二阶线性ADRC可以等效于增加了前馈和二阶低通滤波器PID控制,并提出了按照等效PID参数对二阶线性ADRC调参的方法。崔文庆等[8]说明在中低频段线性ADRC等效于PID控制器串联n阶超前环节。除了根据频域特性和类比PID的调参方法,还有很多自适应调参方法,如基于强化学习改进的自抗扰控制算法在无人船中的应用[9-10]。以上理论分析说明ADRC实际上是改进版的PID,PID是ADRC的一种特殊情况。但是当输入阶跃信号的幅值改变较大时,得到的过渡过程不同,原有的扩张状态观测器对扰动的观测误差将增大,进而影响系统的稳定性,需要重新调节控制器参数,才能取得好的控制效果。
为此,本文提出一种基于RBF神经网络补偿的线性自抗扰控制方法:利用神经网络的自学习和自适应能力,将其用于扰动观测器的改进,实现在不同阶跃信号下对扰动的准确估计,以此改善ADRC的控制性能,简化控制器调参过程,提高控制器的鲁棒性。将改进后的控制器应用于AUV的航向角控制,通过仿真实验说明了方法的有效性,验证了所提方法对不同采样频率的鲁棒性。仿真结果表明,在低采样频率下改进后的控制方法有更好的控制效果,对实际工程具有参考意义。
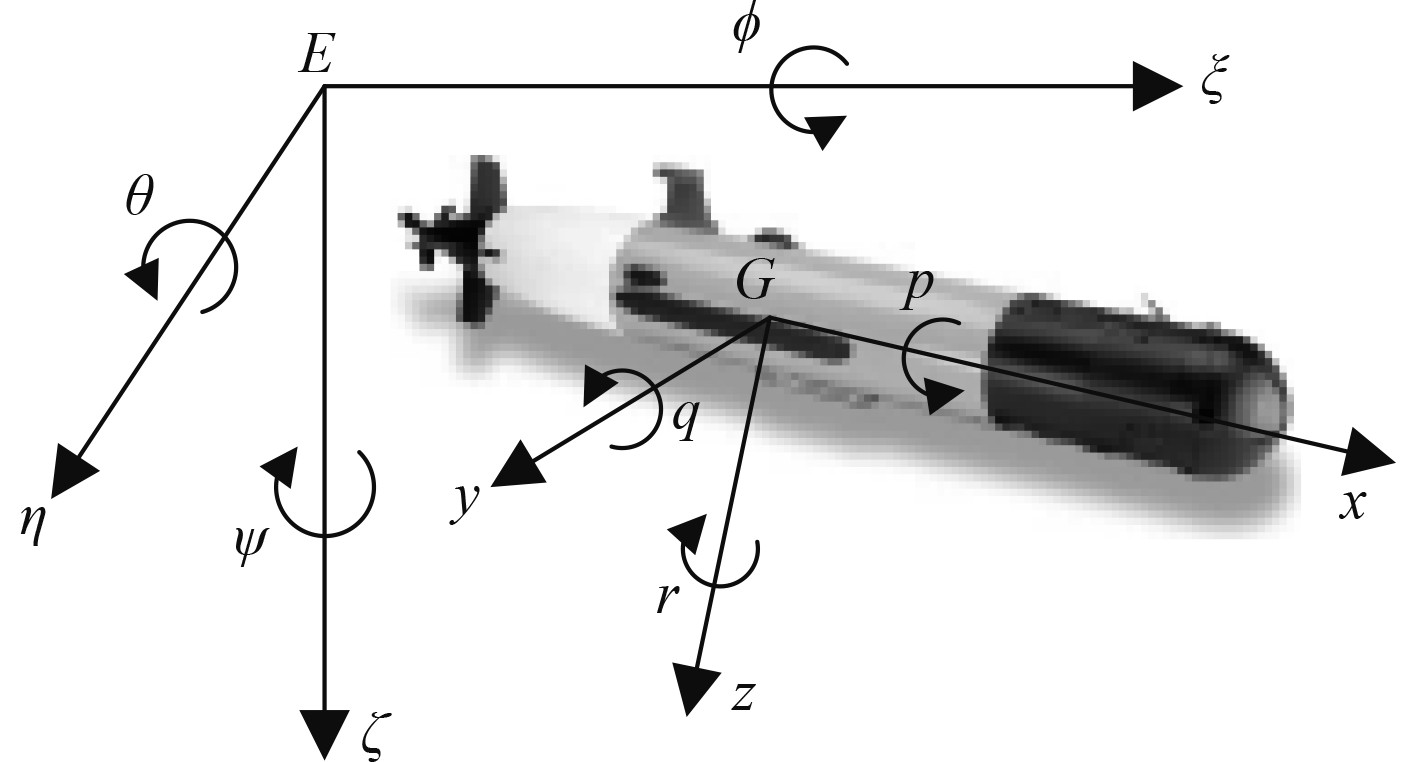
1 AUV模型 1.1 坐标系、术语和符号定义按照国际水池(ITTC)推荐的和造船与轮机工程学会(SNAME)术语公报的体系[11],采用2个右手坐标系表述AUV的运动学和动力学模型:一个是固定于地球上的定坐标系
|
图 1 坐标系和变量示意 Fig. 1 Coordinate systems and parameters |
|
|
表 1 变量对应的符号 Tab.1 Signs of parameters |
将AUV看做自由运动的刚体,根据刚体六自由度运动学方程,AUV位姿和运动速度之间的转换关系表达为:
| $ \left[ \begin{gathered} {{{\dot {{P}}}}} \\ {{{\dot \varTheta }}} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {{T}}&{{{{{{0}}}}_{3 \times 3}}} \\ {{{{0}}_{3 \times 3}}}&{{R}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V}} \\ {{{{\varOmega}} }} \end{array}} \right]。$ | (1) |
式中:
将AUV看做刚体,参考刚体动力学公式推导AUV动力学模型。记
| $ {{{{\boldsymbol{M}}}}_{RB}}{\boldsymbol{\dot v}} + {{{{\boldsymbol{C}}}}_{RB}}({{v}}){{v}} = {{\boldsymbol{\tau }}_{RB}} 。$ | (2) |
式中:
| $ {{\boldsymbol{\tau }}_{RB}} = {\boldsymbol{\tau }} + {{\boldsymbol{\tau }}_{hyd}} + {{\boldsymbol{\tau }}_{hs}} + {{\boldsymbol{\tau }}_{dis}}。$ | (3) |
式中:
由式(2)和式(3)得到AUV状态变量的加速度表达式为:
| $ {{\dot {\boldsymbol{v}}}} = {{{{\boldsymbol{M}}}}^{{\text{ - }}1}}{\boldsymbol{\tau }} - {{{{\boldsymbol{M}}}}^{{\text{ - }}1}}({{{\boldsymbol{C}}}}({{{\boldsymbol{v}}}}){{{\boldsymbol{v}}}} - {{D}}({{{\boldsymbol{v}}}}){{{\boldsymbol{v}}}} - {{{\boldsymbol{g}}}}({{{\boldsymbol{\varTheta}} }}) - {{{{\boldsymbol{g}}}}_0} + {{\boldsymbol{\tau }}_{{{{\boldsymbol{dis}}}}}}) 。$ | (4) |
其中,
实际控制器按照解耦后的模型来设计,所以可以对模型进行合理的简化。假设整个过程中推进器的转速保持不变,AUV处于巡航状态,当控制航向角时,只有垂直舵动作,水平舵微调用于保持纵倾角稳定。基于上述假设,得到航向角控制模型:
| $ \begin{gathered} \ddot \psi = {m_{61}}({X_{prop}} + {X_r}) + {m_{62}}{Y_r} + {m_{64}}{K_{prop}} + {m_{66}}{N_r}+ \\ f(\psi ,\dot \psi ,{w_\psi },t) = b_0^\psi \delta _r^2 + b_1^\psi {\delta _r} + b_2^\psi + f(\psi ,\dot \psi ,{w_\psi },t) 。\end{gathered} $ | (5) |
其中:
ADRC将积分器串联型作为标准型,将总扰动扩张为系统的一个状态,并经观测器估计后补偿到控制输入中加以消除,达到简化控制系统、提高控制抗干扰性的目的。
ADRC由扩张状态观测器(Extended State Observer,ESO)、跟踪微分器(Tracking Differentiator,TD)和状态误差反馈控制律(State Error Feedback,SEF)组成,如图2所示。其中ESO用于估计系统的状态和总扰动,生成补偿量,TD用于配置过渡过程和获取微分信号,SEF用于生成控制信号。

|
图 2 ADRC控制器结构 Fig. 2 Structure of ADRC controller |
设二阶对象:
| $ \ddot y = f(y,\dot y,w,t) + {b_1}\delta 。$ | (6) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot v}_1} = {v_2}},\\ {{{\dot v}_2} = f({v_1},{v_2},w,t) + {b_1}\delta },\\ {y = {v_1}} 。\end{array}} \right. $ | (7) |
将航向角控制模型除控制量一阶项外的部分视为该通道的内部扰动,则式(5)变为:
| $ \ddot \psi = b_1^\psi {\delta _r} + \hat f(\psi ,\dot \psi ,{\delta _r},{w_\psi },t)。$ | (8) |
对比式(6),可对航向角控制应用扩张状态观测器,估计总扰动并补偿到控制信号中。
2.1.1 跟踪微分器TD的算法为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot v}_1} = {v_2}} ,\\ {{{\dot v}_2} = fhan({v_1} - {v_0},{v_2},{r_0},{h_0})} 。\end{array}} \right. $ | (9) |
其中
| $ fhan = \left\{ \begin{array}{*{20}{l}} r{\rm{sign}}(a),&{\left| a \right| > d},\\ r\frac{a}{d},&{\left| a \right| \leqslant d}。\end{array} \right. $ | (10) |
| $ a = \left\{ {\begin{array}{*{20}{l}} {x_2} + \dfrac{{({a_0} + d)}}{2}{\rm{sign}}({x_3}),& {\left| {{x_3}} \right| > {d_0}} ,\\ {x_2} + \dfrac{{{x_3}}}{{{h_0}}},&{\left| {{x_3}} \right| \leqslant {d_0}}。\end{array}} \right. $ | (11) |
式中:
TD的状态变量
ESO是ADRC的核心,其以控制信号δ和输出信号y为输入量,输出对系统状态和总扰动的估计。
将总扰动扩张成新的状态变量:
| $ v{}_3 = f(y,\dot y,w,t)。$ | (12) |
则可对系统式(7)建立线性扩张状态观测器:
| $ \left\{ {\begin{array}{*{20}{l}} {\varepsilon = y - {z_1}},\\ {{{\dot z}_1} = {z_2} + {l_1}\varepsilon },\\ {{{\dot z}_2} = {z_3} + {l_2}\varepsilon + {b_1}\delta },\\ {{{\dot z}_3} = {l_3}\varepsilon } 。\end{array}} \right. $ | (13) |
其中,观测器的状态向量
将总干扰的观测值补偿到控制信号中:
| $ \delta = \frac{{ - {z_3} + {\delta _0}}}{{{b_1}}}。$ | (14) |
忽略
| $ \ddot y = (f - {z_3}) + {\delta _0} \approx {\delta _0} 。$ | (15) |
采用PD控制生成控制信号:
| $ {\delta _0} = {k_p}({v_1} - {z_1}) - {k_d}({v_2} - {z_2})。$ | (16) |
其中,
根据扩张状态观测器的表达式(13),观测器带宽是固定不变的,只对一定频率范围内的干扰估计效果比较好,如果扰动的频率范围较宽,观测效果就会降低,需要重新调整观测器带宽。同时,由于AUV模型具有非线性、耦合、时变的特点,不同阶跃输入和采样频率也会引起内部扰动的变化,影响观测器的效率。针对这一问题,可以用RBF神经网络改进观测器,使之具有自适应特性。
RBF神经网络是20世纪80年代末提出的一种神经网络,能以任意精度逼近任意连续函数,具有学习速度快、避免陷入局部最小值的特点,采用RBF神经网络对系统式(7)中的总扰动进行自适应逼近。
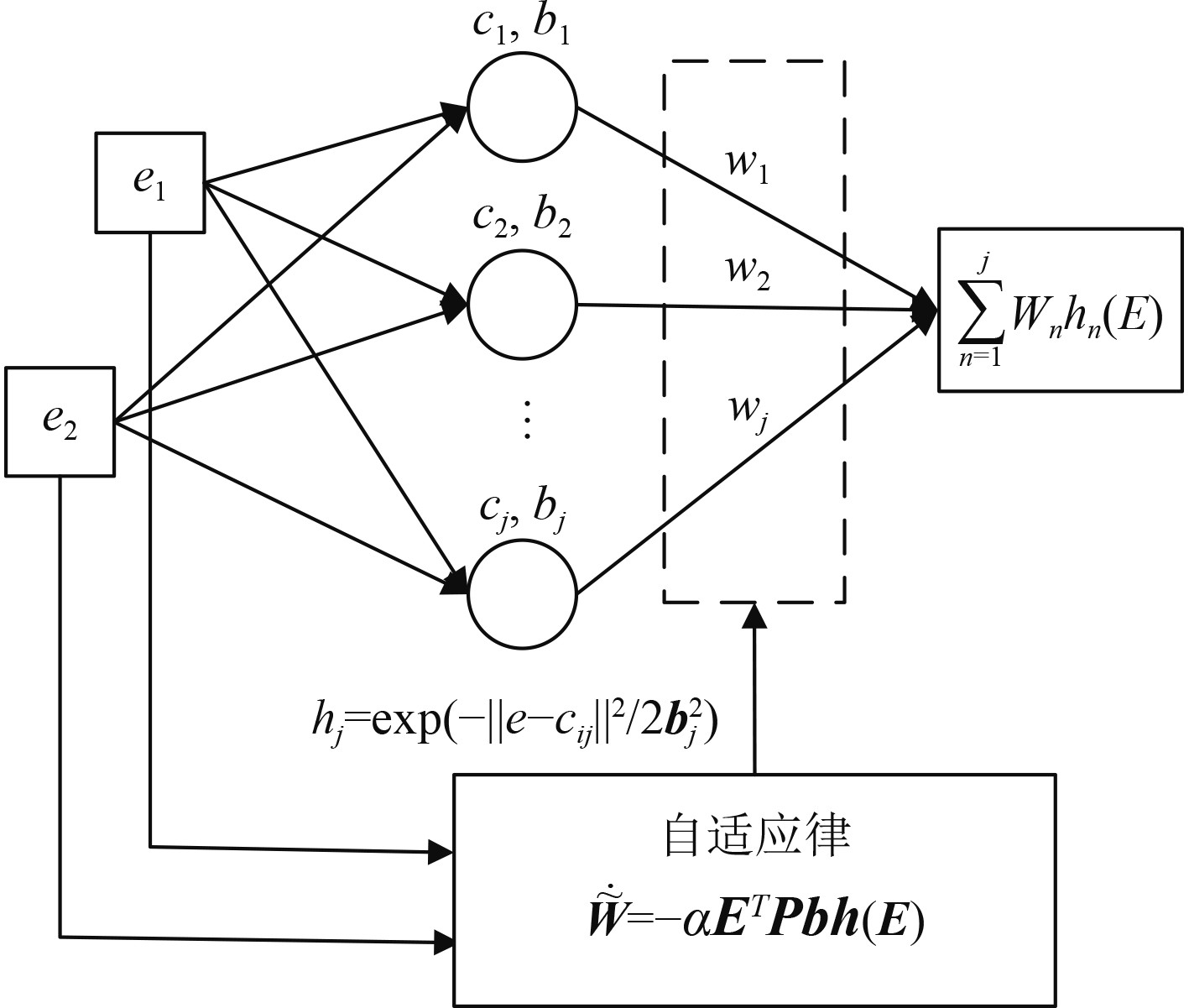
RBFNN是一种3层的神经网络,结构如图3所示,包括输入层、隐层和输出层,输入层到隐层之间为非线性映射,激活函数采用径向基函数:
|
图 3 RBF神经网络结构 Fig. 3 Structure of RBF Neural Network |
| $ {\boldsymbol{h}}({\boldsymbol{x}},{\boldsymbol{c}}) = {\boldsymbol{h}}(\left\| {{\boldsymbol{x}} - {\boldsymbol{c}}} \right\|) 。$ | (17) |
径向基函数取值仅与距中心的距离有关,且两边对称。标准的径向基函数一般取欧式距离,最常用的是高斯核函数。隐层到输出层之间为线性映射,取径向基函数输出值的加权和,权值可以通过自适应律调整,称为自适应径向基函数神经网络。
取RBF神经网络的输入为TD设定值和ESO观测值的误差:
| $ {e_1} = {v_1} - {z_1} ,$ | (18) |
| $ {e_2} = {\dot v_1} - {\dot z_1} = {v_2} - {z_2},$ | (19) |
| $ {\boldsymbol{E}} = {\left[ {\begin{array}{*{20}{c}} {{e_1}}&{{e_2}} \end{array}} \right]^{\text{T}}}。$ | (20) |
采用高斯核RBF神经网络的算法为:
| $ {\boldsymbol{h}}({\boldsymbol{E}}) = \exp ( - {{{{\left\| {{\boldsymbol{E}} - {{\boldsymbol{c}}_{ij}}} \right\|}^2}} /{2{\boldsymbol{b}}_j^2}}),$ | (21) |
| $ f({\boldsymbol{E}}) = {{\boldsymbol{W}}^{\text{T}}}{\boldsymbol{h}}({\boldsymbol{E}}) + \sigma 。$ | (22) |
式中:i为输入层的节点数,j为隐含层的节点数,
| $ \sigma = \hat f({\boldsymbol{E}}|{\boldsymbol{W}}) - f({\boldsymbol{E}}) 。$ | (23) |
| $ {{\boldsymbol{W}}^{\boldsymbol{*}}} = \arg \mathop {\min }\limits_{{\boldsymbol{W}} \in {\boldsymbol{\varOmega }}} \left[ {\sup \left| {\hat f({\boldsymbol{E}}) - f({\boldsymbol{E}})} \right|} \right] 。$ | (24) |
式中,
| ${ \dot {\tilde {{W}}}} = - \alpha {{{E}}^{\text{T}}}{{Pbh}}({{E}}) 。$ | (25) |
此时可使神经网络的逼近误差
| $ {{\boldsymbol{\varLambda }}^{\text{T}}}{\boldsymbol{P}} + {\boldsymbol{P\varLambda }} = - {\boldsymbol{Q}}。$ | (26) |
其中,Q是任意的
| $ {\boldsymbol{\varLambda }} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - {k_p}}&{ - {k_d}} \end{array}} \right]。$ | (27) |
式中,
神经网络的实际输出为:
| $ \tilde f({\boldsymbol{E}}) = {{\boldsymbol{\tilde W}}^{\text{T}}}{\boldsymbol{h}}({\boldsymbol{E}})。$ | (28) |
可以用
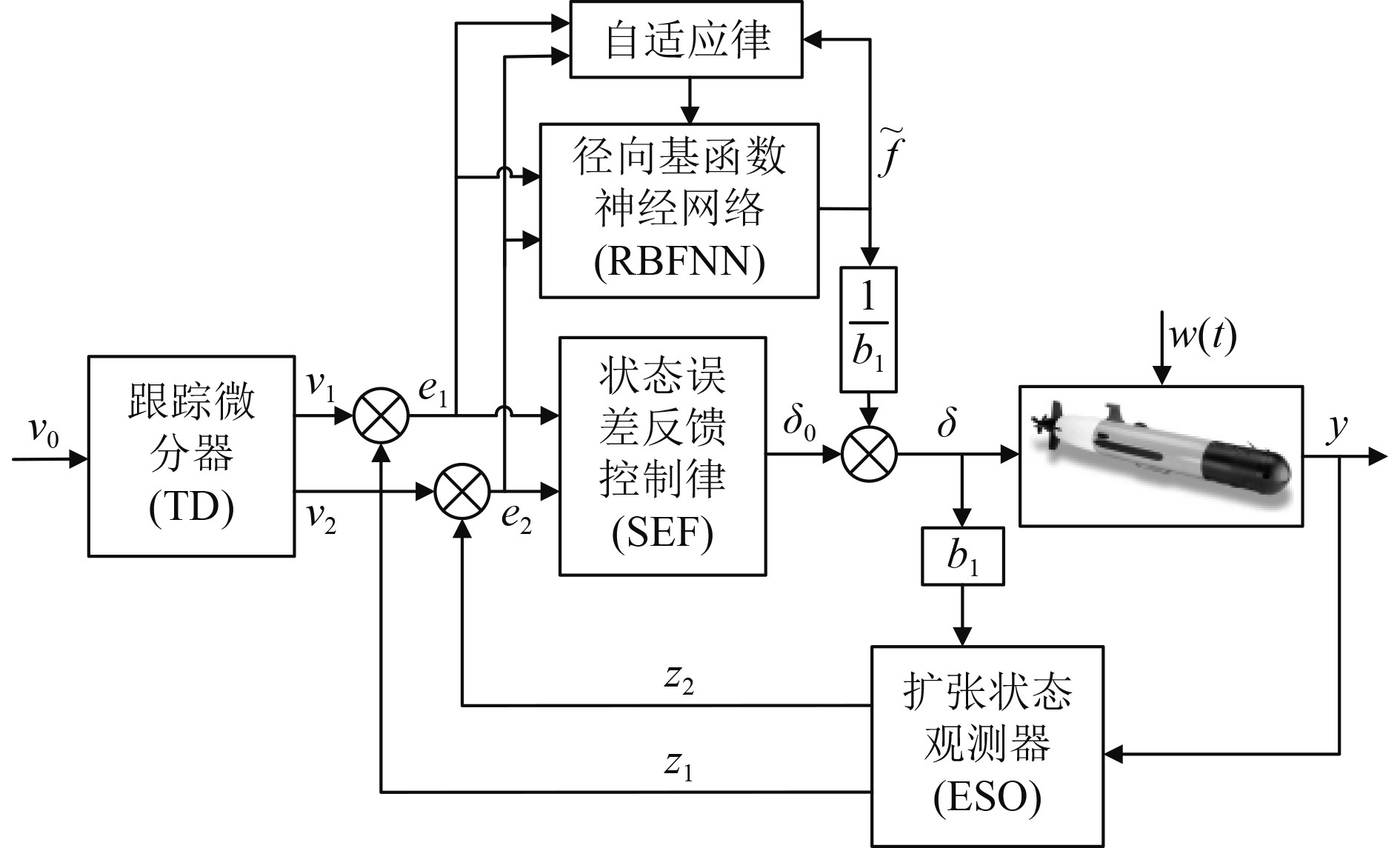
|
图 4 基于RBFNN改进的ADRC控制器结构 Fig. 4 Structure of ADRC controller based on RBFNN |
为了验证本文提出方法的有效性,设计仿真实验。针对AUV姿态控制,分别建立PID、ADRC和ADRC+RBFNN控制器,进行姿态控制仿真。在不同时刻输入不同幅值的阶跃信号,对比控制器的动态响应性能;然后设计控制端扰动和反馈信号噪声,研究控制器对干扰的观测和补偿能力。最后,比较采样频率对改进前后控制器的影响,验证控制器的工程可实现性。
实验中的主要参数包括ADRC的速度因子
|
|
表 2 PID和ADRC控制器参数设置[2] Tab.2 Parameters setting of PID and ADRC controllers |
为了得到准确的结果,仿真中改进方法的参数
为了比较不同阶跃输入下控制器的响应性能,设计了AUV航向角跟踪控制仿真实验。仿真时间总长150 s,分别于0 s、20 s、40 s、90 s时输入幅值为
仿真中采用的参数在阶跃输入为

|
图 5 无外扰时航向角跟踪控制仿真结果 Fig. 5 Simulation results of yaw trajectory tracking without external disturbances |
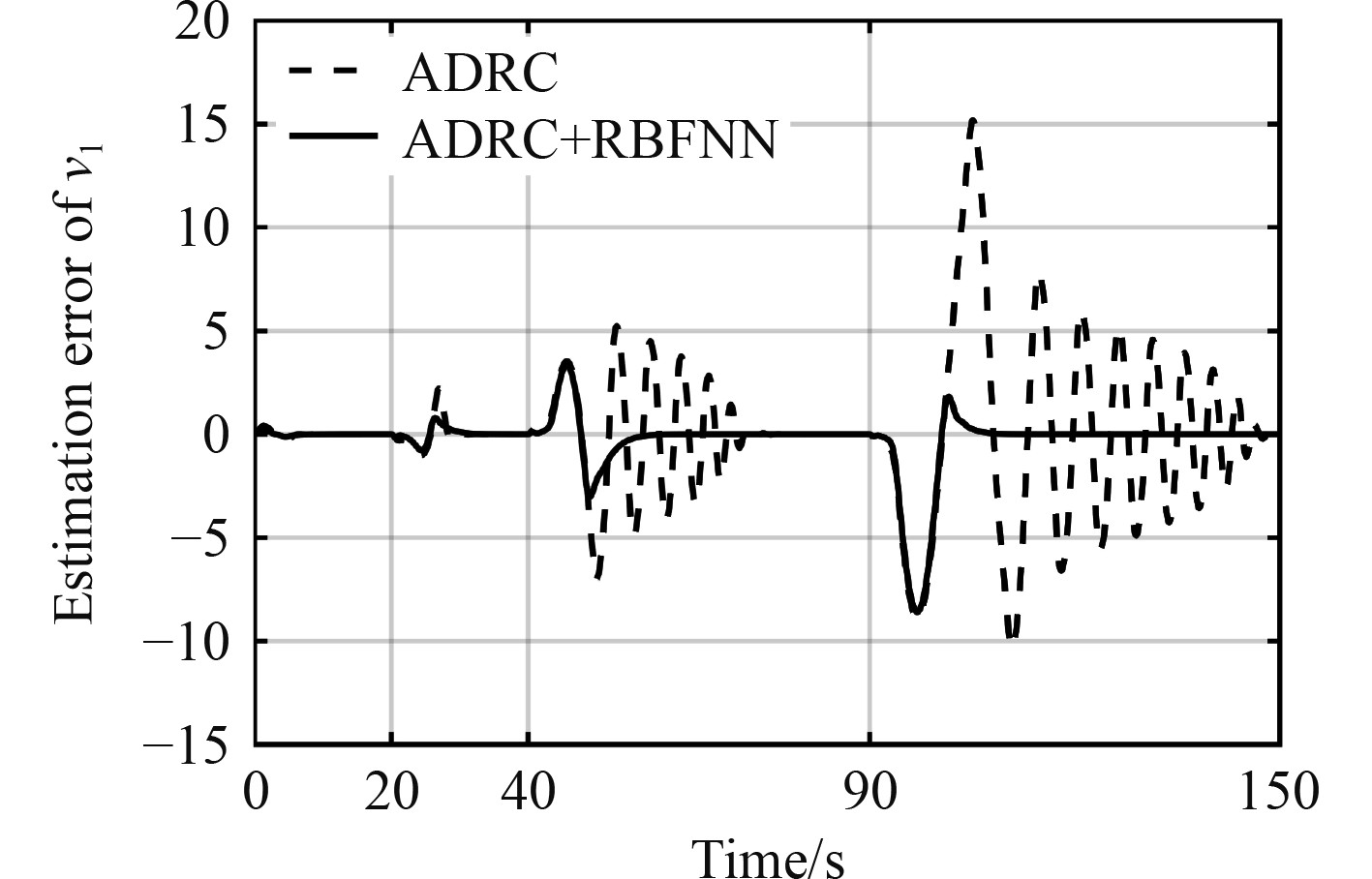
|
图 6
不含外部扰动时
|
|
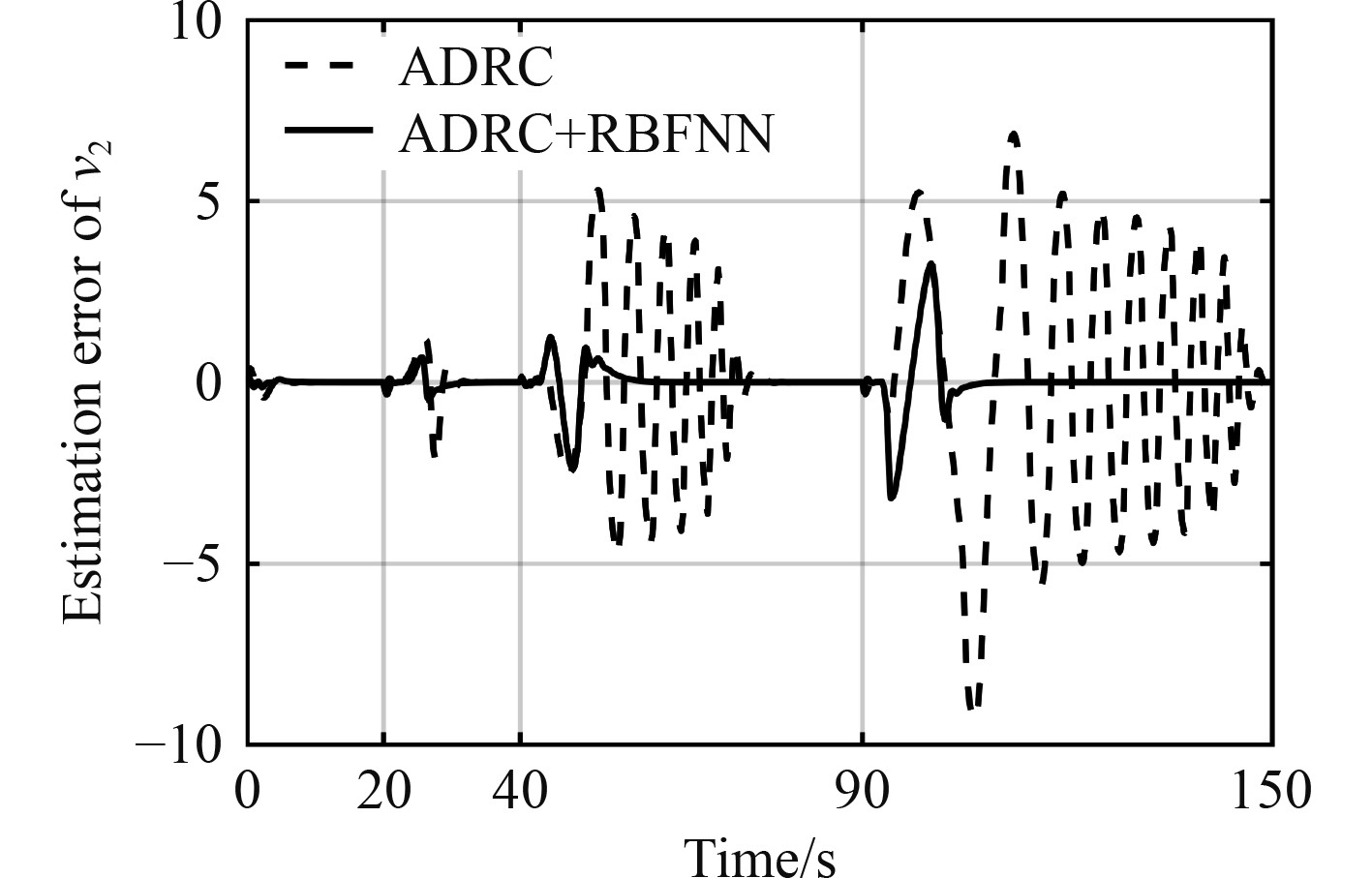
图 7
不含外部扰动时
|
根据仿真结果可以发现,基于ADRC的方法可以取得与PID近似的效果,且在20 s之前对信号的观测误差比较小,说明控制器此时可以准确的观测模型不确定部分和各通道耦合部分。
阶跃输入幅值和过渡过程的不同会影响ADRC的控制效果,结果是当阶跃值增加到
仿真结果说明ADRC+RBFNN方法在不同阶跃信号输入时,对内部扰动和系统状态估计具有自适应能力,能够保证更大范围的稳定性,简化了控制器参数整定过程。
3.1.2 含外部扰动时的仿真实验结果根据文献[17],外部扰动
|
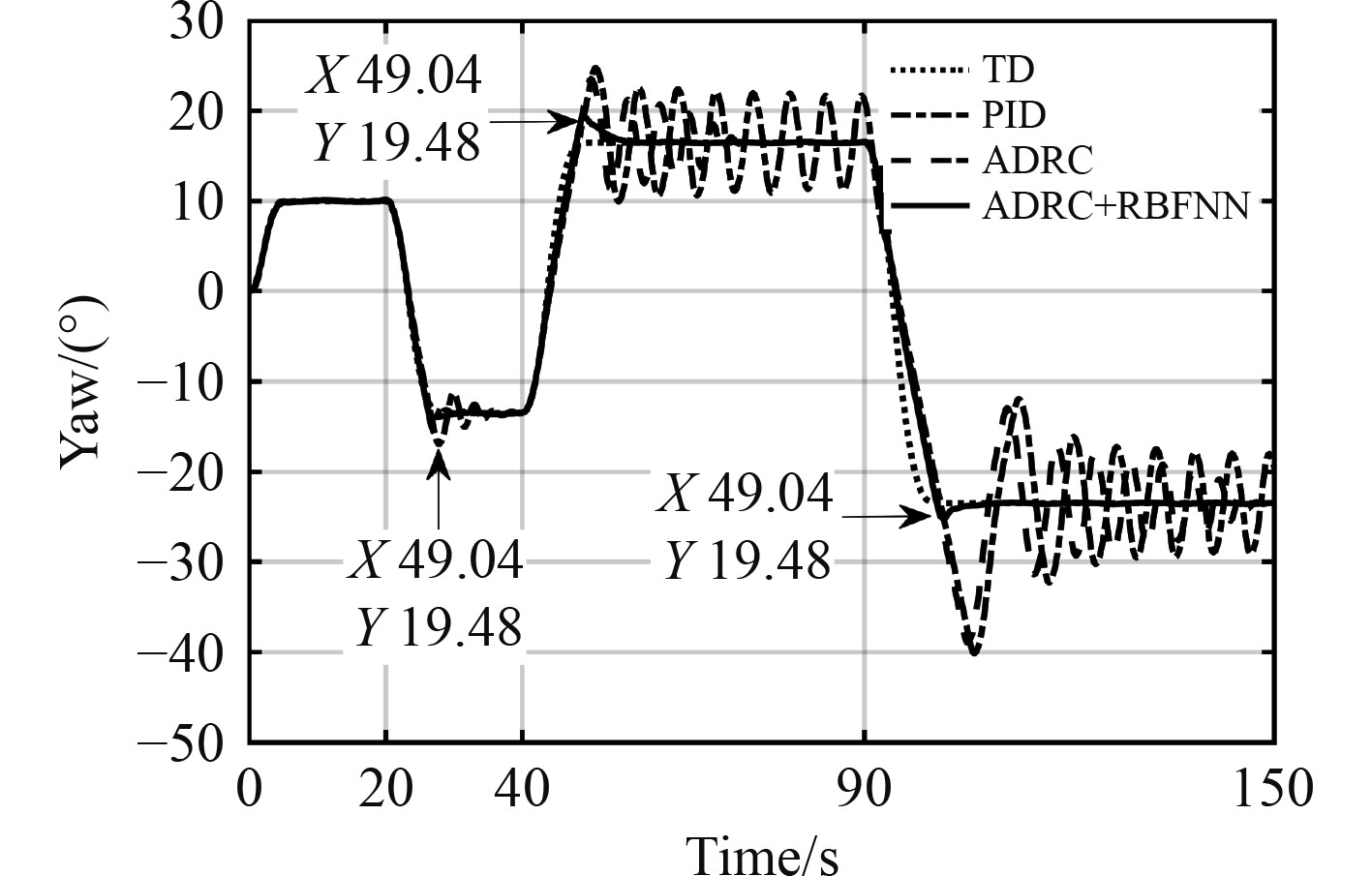
图 8 含外部扰动时航向角跟踪控制仿真结果 Fig. 8 Simulation results of yaw trajectory tracking with external disturbances |
|
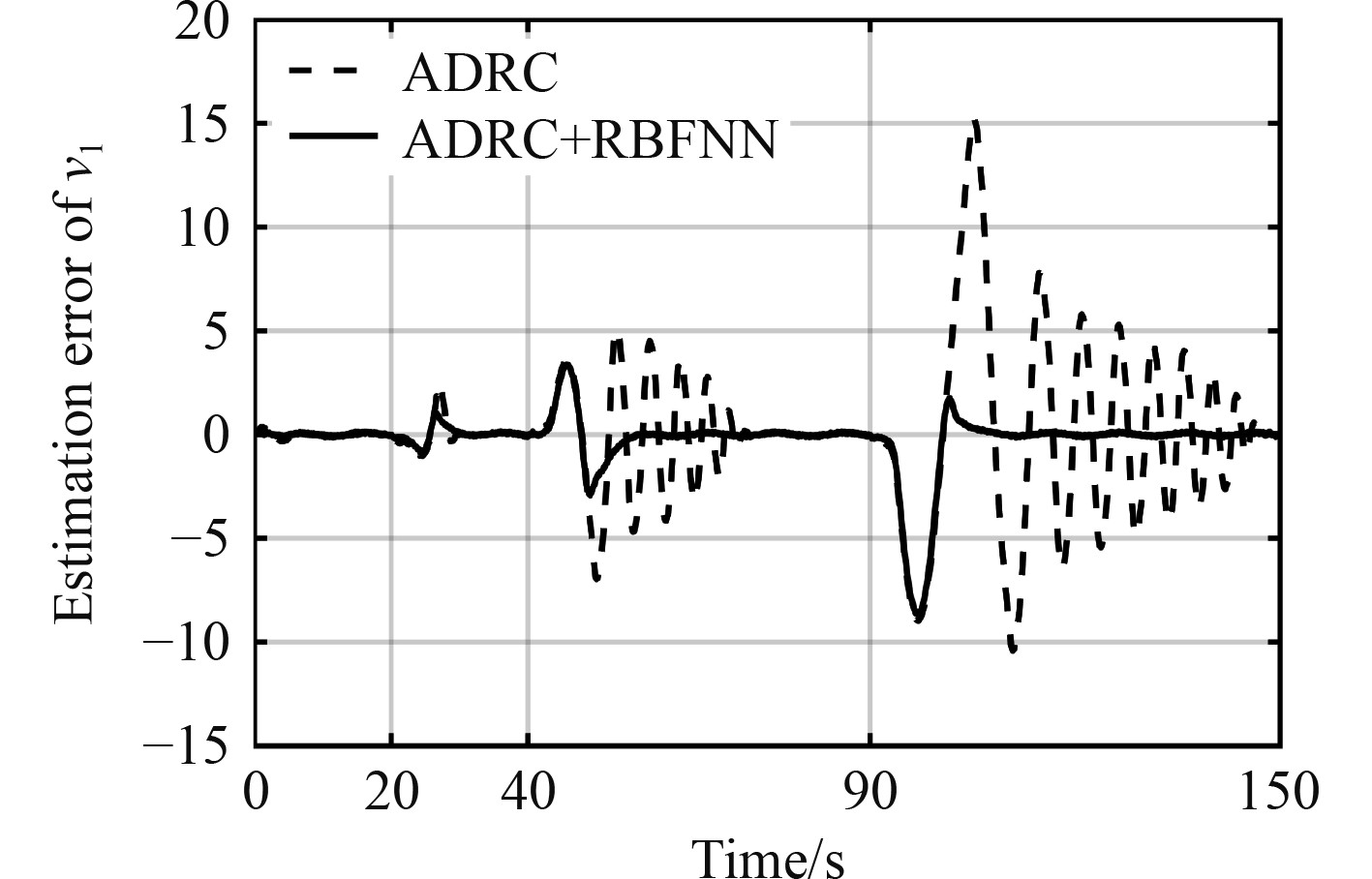
图 9
含外部扰动时
|

|
图 10
含外部扰动时
|

|
图 11 航向角控制扰动估计仿真结果 Fig. 11 Simulation results of disturbances estimated value of controllers |
由图8可知,ADRC控制相对PID具有更好的抗扰动效果,可以更快稳定,但是随着阶跃值的增加,原始ADRC控制发生一定程度的振荡。图9和图10说明此时ADRC对总扰动的估计出现较大误差,图11说明其对控制端扰动的估计出现较大的误差。反观ADRC+RBFNN方法,虽然也会受到阶跃变化的影响,但是总体超调量小于原始ADRC方法,且对扰动和状态量的估计误差能够迅速收敛。
仿真结果说明,相比ADRC控制,本文改进方法能够更好适应不同阶跃输入的变化,对总扰动的估计更加准确,提高了控制器的稳定性和抗干扰能力。
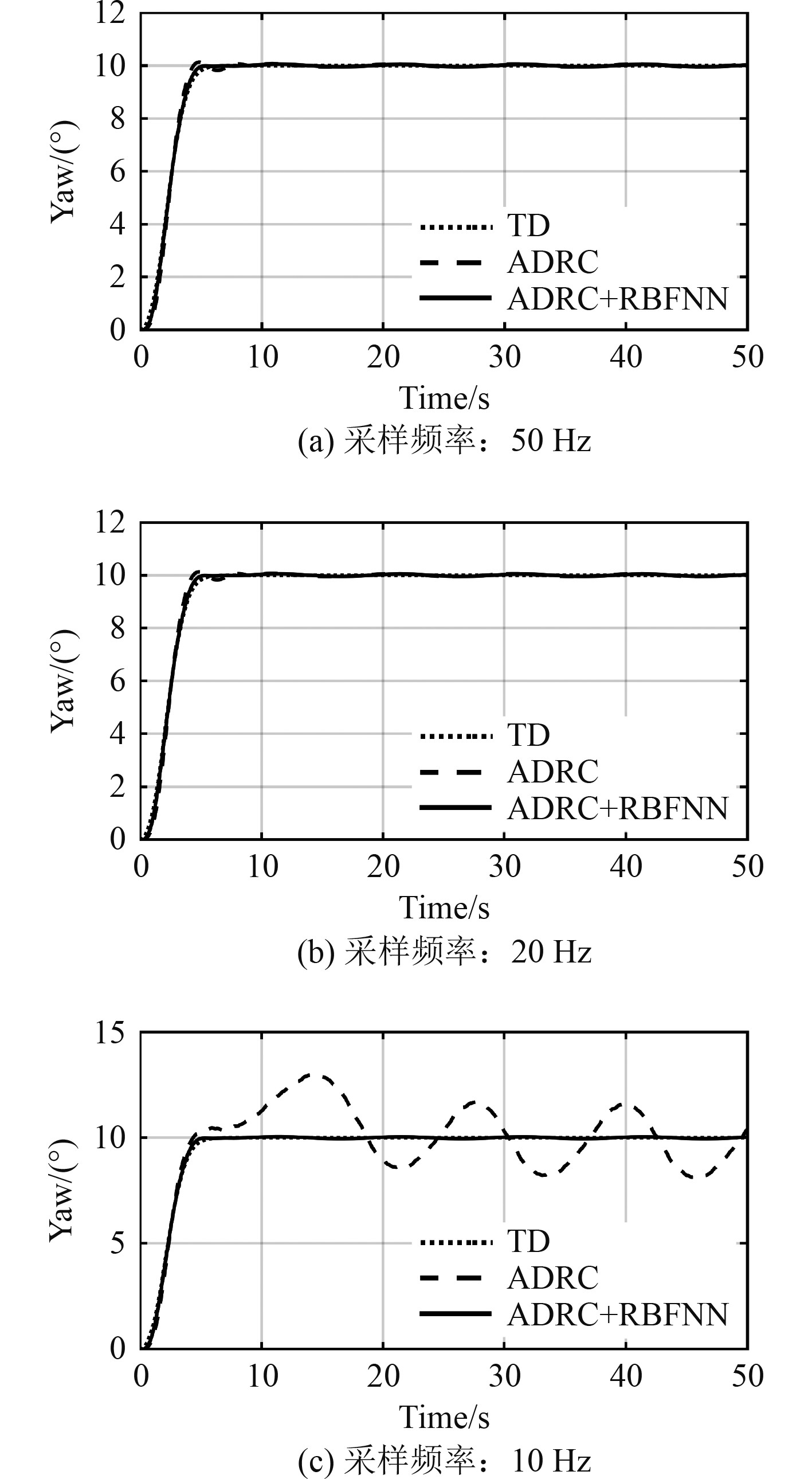
3.2 不同采样频率姿态控制仿真实验由于采样频率会影响扩张状态观测器的效果,而AUV属于大惯性系统,实际平台中的采样频率比较低,有明显的离散特性。为了比较不同采样频率对改进前后控制方法的影响,设计仿真实验。选择采样频率分别为50 Hz、20 Hz、10 Hz,对比控制器的效果,仿真结果如图12所示。
|
图 12 不同采样频率航向角跟踪控制仿真结果 Fig. 12 Simulation results of yaw trajectory tracking control at different sampling frequencies |
仿真结果说明改进后的ADRC+RBFNN控制器在低采样频率下依然能够取得理想的控制效果,进而可以通过嵌入式系统硬件和工业软件组件的方式在实际AUV平台中实现,具有很大的工程应用潜力。
4 结 语针对AUV作业过程中存在的环境干扰,为了提高在不同阶跃输入和采样频率下的扰动观测能力和抗干扰能力,本文提出一种基于RBF神经网络补偿的新型自抗扰控制方法。在线性ADRC控制的基础上,将自适应RBF神经网络应用于改进扩张状态观测器,提升了扰动估计的快速性、准确性。仿真实验证明,改进后的ADRC在不同阶跃输入下对扰动和系统状态的观测更加准确,控制器跟踪航向角能够更快达到稳定值,且适用于低采样频率。
后续工作将重点研究本文方法在AUV平台中的应用问题,通过水池和开放水域实验验证本文提出方法的有效性。
| [1] |
黄琰, 李岩, 俞建成, 等. AUV智能化现状与发展趋势[J]. 机器人, 2020, 42(2): 215-231. HUANG Yan, LI Yan, YU Jiancheng, et al. State-of-the-art and development trends of AUV intelligence[J]. ROBOT, 2020, 42(2): 215-231. |
| [2] |
HAN J Q. From PID to Active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [3] |
ZHANG Y N, DENG H, LI Y Z. Depth control of AUV using sliding mode active disturbance rejection control[C]// 2018 3rd International Conference on Advanced Robotics and Mechatronics (ICARM), 2018: 300–305.
|
| [4] |
RAOUF F, SOFIANE K, MAHMOUD Y, et al. Active disturbance rejection control for robotic systems: A review[J]. Mechatronics, 2021, 80, 102671, ISSN 0957-4158.
|
| [5] |
LI M N, ZHANG W, S B. Path track control of underwater vehicle based on active disturbance rejection control[C]// 2021 33rd Chinese Control and Decision Conference (CCDC), 2021, pp. 4658–4663.
|
| [6] |
GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the 2003American Control Conference, 2003, 4989–4996.
|
| [7] |
JIN H Y, SONG J C, LAN W Y. On the characteristics of ADRC: a PID interpretation[J]. Science in China, 2020, 63(10): 254–256.
|
| [8] |
崔文庆, 王雨桐, 谭文. 用PID控制近似线性自抗扰控制[J]. 控制理论与应用, 2020, 37(8): 1781-1789. |
| [9] |
CHEN Z Q, QIN B B, SUN M W. Q-Learning-based parameters adaptive algorithm for active disturbance rejection control and its application to ship course control[J]. Neurocomputing, 2020, 408: 51-63. DOI:10.1016/j.neucom.2019.10.060 |
| [10] |
QIN H Y, TAN P L, CHEN Z Q, et al. Deep reinforcement learning based active disturbance rejection control for ship course control[J]. Neurocomputing, 2022, 484: 99-108. DOI:10.1016/j.neucom.2021.06.096 |
| [11] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 2021: 10–11.
|
| [12] |
FOSSEN, THOR I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons Ltd, 2021.
|
| [13] |
杨超, 张铭钧, 吴珍臻, 等. 作业型水下机器人纵、横倾姿态自适应区域控制方法[J]. 机器人, 2021, 43(2): 224–233.
|
| [14] |
CHEN Z, ZHANG Y G, NIE Y, et al. Adaptive sliding mode control design for nonlinear unmanned surface vessel using rbfnn and disturbance-observer[J]. IEEE Access, 2020, 8: 45457-45467. DOI:10.1109/ACCESS.2020.2977609 |
| [15] |
LIU W T, ZHAO T. An active disturbance rejection control for hysteresis compensation based on neural networks adaptive control[J]. ISA Transactions, 2021, 109: 81-88. DOI:10.1016/j.isatra.2020.10.019 |
| [16] |
CHEN X, LI D H, GAO Z Q et al. Tuning method for second-order active disturbance rejection control[C]// Processings of the 30th Chinese Control Conference, 2011, pp. 6322–6327.
|
| [17] |
袁东, 马晓军, 曾庆含, 等. 二阶系统线性自抗扰控制器频带特性与参数配置研究[J]. 控制理论与应用, 2013, 30(12): 1630-1640. |
 2023, Vol. 45
2023, Vol. 45
