2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Lab on Ship Vibration and Noise, Wuhan 430033, China
目前,大量采用线性隔振元件解决工程隔振问题[1]。然而,对于某些工程问题而言,需要实现低频隔振,甚至极低频隔振。若仍采用线性隔振方式,要实现低频隔振势必要降低隔振系统的刚度,这不仅会降低隔振系统的静态稳定性,在一些复杂工况下,如摇摆、冲击,还会导致隔振器变形过大,影响系统稳定性。使用非线性隔振器可以解决上述问题,在一系列参数设定下,实现高静态刚度低动态刚度特性,此类隔振器被称为准零刚度(Quasi-zero stiffness,QZS)隔振器[2]。准零刚度隔振装置的动力学特性方程可以由具有三次非线性项Duffing振子模型描述[3]。
Kovacic[4]设计了一种由2个有预压、非线性斜向弹簧与线性垂向弹簧并联的准零刚度隔振器,研究了该隔振器实现准零刚度的条件及在非对称激励下的动力学响应,结果表明该模型在平衡位置的准零刚度特性与初始弹簧的几何关系,斜向弹簧的预压程度、刚度有关,然而动力学分析表明该模型在非对称激励下,在一定激励频率范围内,会产生周期倍增的分叉,最终会产生混沌行为。Carrella [5]在Kovacic的研究基础上做了进一步推广,将2个斜弹簧分为有预压的线性弹簧、有预压的非线性弹簧以及无预压的线性弹簧这3种情况进行静力学分析,研究了3种模型在对称激励下的动力学特性,结果表明3种情况的准零刚度隔振装置的隔振效果都比原线性系统的隔振效果好,其中斜弹簧为有预压的非线性弹簧隔振效果最佳。Brennan[6]总结了前人对Duffing振子的研究,给出了对于小阻尼Duffing振子在简谐激励下的跳跃频率和该频率下响应幅值的表达式,比较了谐波平衡法与微扰法求解方程的误差,结果表明向上跳跃频率与系统的非线性度和激励力的幅值有关,向下跳跃频率不仅与上述因素有关还与系统阻尼有关。彭献[7]研究了三弹簧连杆机构准零刚度隔振器,侧向弹簧只在水平方向移动,其隔振性能优于非线性隔振器,当隔离随机振动时,宜隔运动而不宜隔离力。任旭东[8]基于空气弹簧隔振器,设计了一种三气囊连杆结构的准零刚度隔振装置,结果表明当在相同激励幅值的条件下,空气弹簧准零刚度隔振系统相对于单个空气弹簧隔振系统能够隔离更低频的振动,且当激励频率大于空气弹簧准零刚度隔振系统的向下跳跃频率时,空气弹簧准零刚度隔振系统具有更好的隔振性能。
本文提出一种五弹簧准零刚度隔振装置模型(简称为五弹簧装置),推导了模型的静力学关系,利用近似回复力并借助带有三次非线性项的Duffing振子动力学方程进行模型的动力学分析,分析该隔振装置的稳定性,并研究不同参数对该隔振装置力传递率的影响。
1 准零刚度隔振装置力学模型建立 1.1 准零刚度隔振装置模型静力学关系推导本文的准零刚度隔振装置布置如图1所示。斜置弹簧原长为y,初始压缩量为

|
图 1 五弹簧准零刚度隔振装置模型 Fig. 1 Five-springs quasi-zero-stiffness vibration isolator model |
取向下为正方向,假设不存在垂向弹簧时,仅分析4个斜置弹簧力学特性,当外力
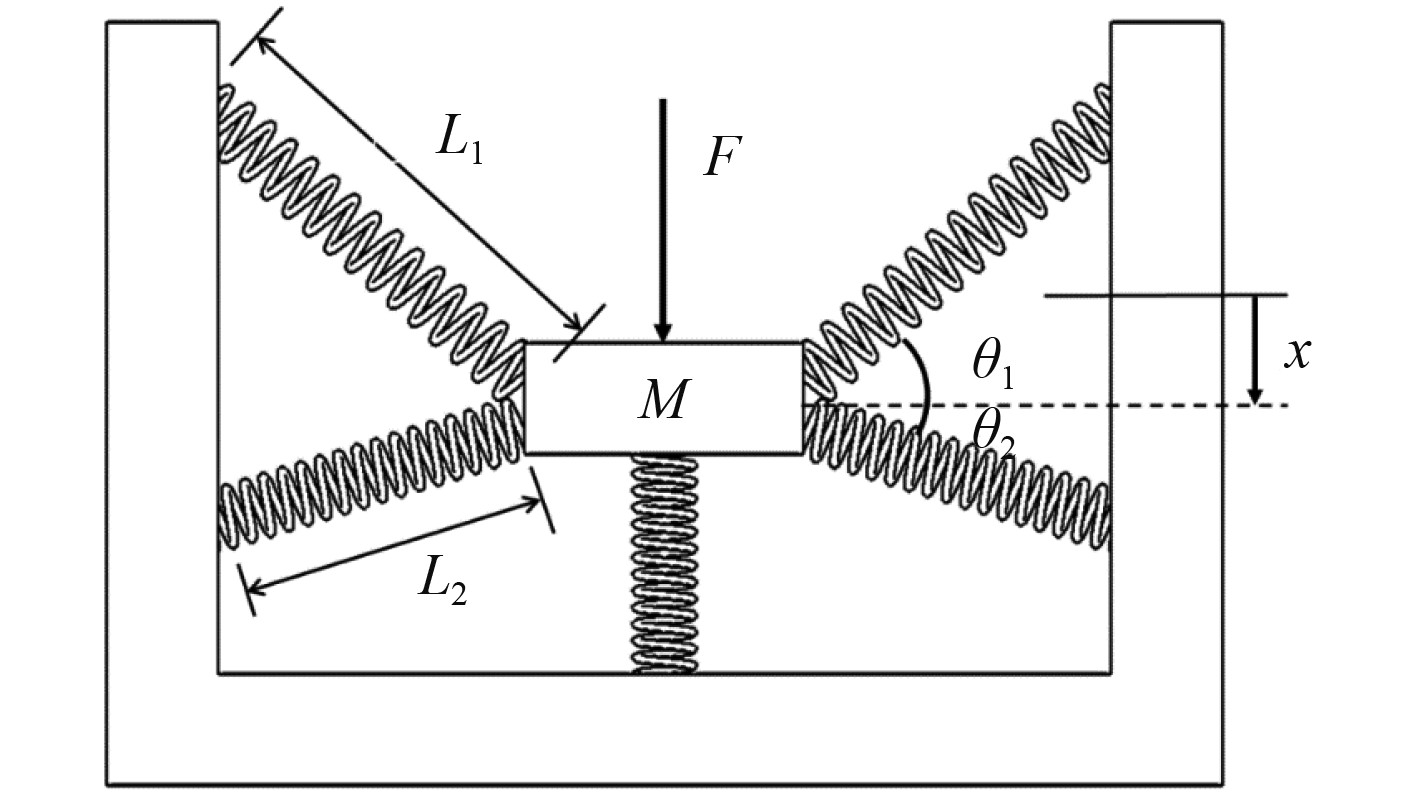
|
图 2 五弹簧准零刚度隔振装置受力作用后任意时刻 Fig. 2 A time when five-springs QZS vibration isolator model forced |
| $ f = - 2{k_d}({L_0} + \delta - {L_1})\sin {\theta _1} + 2{k_d}({L_0} + \delta - {L_2})\sin {\theta _2} 。$ | (1) |
式中:
引入无量纲参数:
| $ \widehat{x}=\frac{x}{{L}_{0}}\text{,}\gamma =\frac{a}{{L}_{0}}=\mathrm{cos}{\theta }_{0}\text{,}\widehat{\delta }=\frac{\delta }{{L}_{0}},$ | (2) |
将式(1)无量纲化,得
| $ {\begin{split} \frac{f}{{{k_d}{L_0}}}{\text{ = }}&2\left( {\sqrt {1 - {\gamma ^2}} - \hat x} \right) \times\left( { - 1 + \frac{{1 + \hat \delta }}{{\sqrt {1 - 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }}} \right) +\\ & 2\left( {\sqrt {1 - {\gamma ^2}} + \hat x} \right) \times \left( {1 - \frac{{1 + \hat \delta }}{{\sqrt {1 + 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }}} \right) 。\end{split} }$ | (3) |
该式的适用范围为
当垂直弹簧存在时,设垂向弹簧刚度为
| $ {\widehat{F}}_{r}=\frac{{F}_{r}}{{k}_{u}{L}_{0}}\text{,}\widehat{k}=\frac{{k}_{d}}{{k}_{u}} 。$ | (4) |
该装置系统无量纲回复力
| $ \tag{5-a} \begin{split} {{\hat F}_r} =& \hat x + 2\hat k\left( {\sqrt {1 - {\gamma ^2}} - \hat x} \right) \times \left( { - 1 + \frac{{1 + \hat \delta }}{{\sqrt {1 - 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }}} \right)+\\ &2\hat k\left( {\sqrt {1 - {\gamma ^2}} + \hat x} \right) \times \left( {1 - \frac{{1 + \hat \delta }}{{\sqrt {1 + 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }}} \right),\\[-25pt] \end{split} $ |
| $ \tag{5-b} \begin{split} {{\hat K}_D} = &1 + 4\hat k + \frac{{2\hat k(1 + \hat \delta ){{(\sqrt {1 - {\gamma ^2}} - \hat x)}^2}}}{{{{(1 - 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2})}^{3/2}}}} -\\ &\frac{{2\hat k(1 + \hat \delta )}}{{\sqrt {1 - 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }} + \frac{{2\hat k(1 + \hat \delta ){{(\sqrt {1 - {\gamma ^2}} + \hat x)}^2}}}{{{{(1 + 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2})}^{3/2}}}} -\\ &\frac{{2\hat k(1 + \hat \delta )}}{{\sqrt {1 + 2\sqrt {1 - {\gamma ^2}} \hat x + {{\hat x}^2}} }}。\\[-25pt] \end{split} $ |
对于不同的

|
图 3
|

|
图 4
|

|
图 5
|
为准确获得准零刚度特性,需满足平衡位置
| $ {\hat K_D} = 1 + 4\hat k - 4\hat k(1 + \hat \delta ) + 4\hat k(1 - {\gamma ^2})(1 + \hat \delta ){\text{ = }}0 ,$ |
| $ \hat k = \frac{1}{{4((1 + \hat \delta ){\gamma ^2} - 1)}} 。$ | (7) |
式中:
| $ \sqrt {1/(1 + \hat \delta )} < \gamma < 1 。$ | (8) |
将参数条件(7)代入式(5-b)可以得到下式:
| $ {{\hat K_{D - QZS}} = \frac{1}{2}\left( \begin{gathered} 2 + \frac{2}{{ - 1 + {\gamma ^2}(1 + \hat \delta )}} \\ + \frac{{{{(\hat x - \sqrt {1 - {\gamma ^2}} )}^2}(1 + \hat \delta )}}{{{{(1 + {{\hat x}^2} - 2\hat x\sqrt {1 - {\gamma ^2}} )}^{3/2}}( - 1 + {\gamma ^2}(1 + \hat \delta ))}} \\ - \frac{{1 + \hat \delta }}{{\sqrt {1 + {{\hat x}^2} - 2\hat x\sqrt {1 - {\gamma ^2}} } ( - 1 + {\gamma ^2}(1 + \hat \delta ))}} \\ + \frac{{{{(\hat x + \sqrt {1 - {\gamma ^2}} )}^2}(1 + \hat \delta )}}{{{{(1 + {{\hat x}^2} + 2\hat x\sqrt {1 - {\gamma ^2}} )}^{3/2}}( - 1 + {\gamma ^2}(1 + \hat \delta ))}} \\ - \frac{{1 + \hat \delta }}{{\sqrt {1 + {{\hat x}^2} + 2\hat x\sqrt {1 - {\gamma ^2}} } ( - 1 + {\gamma ^2}(1 + \hat \delta ))}} \\ \end{gathered} \right) 。} $ | (9) |
将符合式(8)要求的不同
由图6可以看出,当

|
图 6
|
选取

|
图 7
|
在动力学分析中,使用近似无量纲回复力进行代替原无量纲回复力表达式。
假设质量
| $ {\widehat{F}}_{rapp}={\widehat{F}}_{r}(0)+{{\widehat{F}}^{\prime }}_{r}(0)\widehat{x} +\frac{{{\widehat{F}}^{″}}_{r}(0){\widehat{x}}^{2}}{2!}+\frac{{{\widehat{F}}^{‴}}_{r}(0){\widehat{x}}^{3}}{3!}+\cdots 。$ | (10) |
设五弹簧装置在平衡位置的最小刚度
| $ {\hat K_{\min }}{\text{ = }}{\hat F'_r}(0) = 1 - 4\hat k\hat \delta + 4\hat k(1 + \hat \delta )(1 - {\gamma ^2}) = 0 。$ | (11) |
式(11)可变为
| $ \hat \delta {\text{ = }}\frac{{1 + 4\hat k - 4\hat k{\gamma ^2}}}{{4\hat k{\gamma ^2}}} 。$ | (12) |
代入式(10),得到近似无量纲回复力
| $ \tag{13-a}{\hat F_{rapp}} = \frac{1}{2}(1 + 4\hat k)( - 4 + 5{\gamma ^2}){\hat x^3} ,$ |
| $ \tag{13-b} {F_{rapp}} = \frac{1}{2}{k_u}{L_0}(1 + 4\hat k)( - 4 + 5{\gamma ^2}){\hat x^3} 。$ |
比较式(13-a)与式(5-a),在泰勒三阶展开下得到的近似回复力

|
图 8
五弹簧准零刚度隔振装置回复力曲线比较图
Fig. 8
Comparison of restoring force curves of the five-spring QZS vibration isolator when
|
可以看出,近似回复力
假设隔振装置的阻尼为线性粘性阻尼,其阻尼系数为

|
图 9 五弹簧隔振装置等效单自由度模型 Fig. 9 Equivalent SDOF system of the five-spring QZS vibration isolator |
当施加谐波激励力
| $ M\ddot x + c\dot x + {F_{rapp}} = F\cos (\omega t) 。$ |
将式(13-b)代入式(14)可以得到装置的无量纲运动微分方程:
| $ \ddot {\hat x} + 2\xi \dot {\hat x} + \kappa {\hat x^3} = \hat F\cos (\varOmega \tau ) 。$ | (15) |
其中:
设装置在谐波激励条件下的稳态响应解为:
| $\tag{16-a} \hat x = A\cos (\varOmega \tau + \varphi ) ,$ |
| $\tag{16-b} \dot {\hat x} =- \varOmega A\sin (\Omega \tau + \varphi ) ,$ |
| $ \tag{16-c} \ddot {\hat x} =- {\varOmega ^2}A\cos (\Omega \tau + \varphi ),$ |
对于该隔振装置,将式(16)代入式(15),得到
| $ \begin{split} & - {\varOmega ^2}A\cos (\varOmega \tau + \varphi ) - 2\xi \varOmega A\sin (\varOmega \tau + \varphi ) \\ & + \kappa {A^3}{\cos ^3}(\varOmega \tau + \varphi ) = \hat F\cos (\varOmega \tau ) 。\end{split} $ |
利用三角变换并令各谐波项和常数项的系数等于0,同时忽略高阶谐波项,可以得到系统稳态响应解表达式为:
| $ {A^2}{\varOmega ^4} + (4{\xi ^2}{A^2} - \frac{3}{2}\kappa {A^4}){\varOmega ^2} + \frac{9}{{16}}{\kappa ^2}{A^6} - {\hat F^2} = 0 。$ | (18) |
为了得到向下跳跃频率,将共振频率
| $ {\varOmega _{1,2}} = \sqrt {\frac{{3{A^4}\kappa - 8{A^2}{\xi ^2} \pm 4\sqrt {{A^2}{{\hat F}^2} - 3{A^6}\kappa {\xi ^2} + 4{A^4}{\xi ^4}} }}{{4{A^2}}}} 。$ | (19) |
当
| $\tag{20-a} {A_{\max }} = \sqrt {\frac{{2{\xi ^3} + \sqrt {4{\xi ^6} + 3\kappa {{\hat F}^2}} }}{{3\xi \kappa }}} ,$ |
| $\tag{20-b} {\varOmega _{\max }} = \frac{1}{2}\sqrt {3{A^2}\kappa - 8{\xi ^2}} 。$ |
同时,为了找到向上跳跃频率发生的位置,令阻尼
| $\tag{21-a} {A_u} = \sqrt[3]{{\frac{{2\hat F}}{{3\kappa }}}} ,$ |
| $\tag{21-b} {\varOmega _u} = \dfrac{{{{\left(\dfrac{3}{2}\right)}^{1/3}}\left(\hat F{{\left(\dfrac{{\hat F}}{\kappa }\right)}^{1/3}} + 2\sqrt { - \hat F{{\left(\dfrac{{\hat F}}{\kappa }\right)}^{5/3}}\kappa } \right)}}{{2{{\left(\dfrac{{\hat F}}{\kappa }\right)}^{2/3}}}} 。$ |
为比较五弹簧装置隔振效果,构建单个弹簧隔振装置等效自由度模型,如图10所示。

|
图 10 单个隔振装置等效单自由度模型 Fig. 10 Equivalent SDOF system of the one-spring vibration isolator |
当同样给系统施加谐波激励力
| $ \ddot {\hat x} + 2\xi \dot {\hat x} + \hat x = \hat F\cos (\varOmega \tau ) 。$ |
同样可以得到其共振频率
| $ {\varOmega _{1,2 - {\rm{single}}}}{\text{ = }}\sqrt {1 - 2{\xi ^2} \pm \frac{{\sqrt {{A^2}({{\hat F}^2} - 4{A^2}{\xi ^2} + 4{A^2}{\xi ^4})} }}{{{A^2}}}} 。$ | (23) |
对于简谐波激励条件下的系统,采用绝对力传递率作为评价其隔振性能的指标,并定义为
| $ \left| T \right| = \left| {\frac{{{{\hat F}_t}}}{{\hat F}}} \right| ,$ | (24) |
式中:
| $ {\hat f_t} = 2\xi \dot {\hat y} + \kappa {\hat y^3}。$ | (25) |
利用谐波平衡法将
| $ {\hat F_t} = \sqrt {{{\left(\frac{3}{4}\kappa {A^3}\right)}^2} + {{(2\xi \varOmega A)}^2}} 。$ | (26) |
将式(26)代入式(24),并使用式(19)中得到的
| $ {\left| T \right|_{{\rm{five}}}} = \sqrt {\frac{{\dfrac{9}{{16}}{\kappa ^2}{A^6} + 4{\xi ^2}\varOmega _{1,2}^2{A^2}}}{{{{\hat F}^2}}}} 。$ | (27) |
同理,可得到单个弹簧隔振装置的传递率表达式:
| $ {\hat F_{t - {\rm{single}}}} = \sqrt {{\text{ }}\left( {4{\xi ^2}{\varOmega ^2} + 1} \right){A^2}} ,$ | (28) |
| $ {\left| T \right|_{{\rm{single}}}} = \sqrt {\frac{{\left( {1 + 4{\xi ^2}{\varOmega ^2}} \right){A^2}}}{{{{\hat F}^2}}}} 。$ | (29) |
准零刚度隔振装置由于存在多个稳态响应解,从而会出现跳跃现象,其中包括与系统阻尼比相关的向上跳跃,以及出现稳态响应幅值最大值对应的向下跳跃。
使用马蒂厄方程判别法,引入扰动变量
| $ \hat x = A\cos (\Omega \tau + \varphi ) + \hat \varepsilon (\tau ) 。$ | (30) |
将式(30)代入五弹簧装置的无量纲微分方程式(15),能够得到该微小扰动的微分方程:
| $ \ddot {\hat \varepsilon} (\tau ) + 2\xi \dot {\hat \varepsilon} (\tau ) + \frac{3}{2}\kappa {A^2}\left[ {1 + \cos 2(\varOmega \tau + \varphi )} \right]\hat \varepsilon (\tau ) = 0 。$ | (31) |
式(31)为含有阻尼的Mathieu方程,可变为:
| $ {\varOmega ^2}\hat \varepsilon '' + 2\xi \varOmega \hat \varepsilon ' + \frac{3}{2}\kappa {A^2}\left[ {1 + \cos \left( {2\psi } \right)} \right]\hat \varepsilon = 0 。$ | (32) |
式中,
设式(32)的解为:
| $ \hat \varepsilon = {C_1}\cos \left( \psi \right) + {C_2}\sin \left( \psi \right) 。$ | (33) |
将式(33)代入式(32),同时利用三角函数变换并忽略高阶谐波项得到多项式方程组,使其方程组判别式等于0,能够得到稳定性判定边界条件。
| $ \Delta = {\varOmega ^4} + \left( {4\xi - 3\kappa {A^2}} \right){\varOmega ^2} + \frac{{27}}{{16}}{\kappa ^2}{A^4} = 0 ,$ | (34) |
| $ {\varOmega _{\Delta 1,2}} = \sqrt {\frac{{6{A^2}\kappa - 8\xi \pm \sqrt {9{A^4}{\kappa ^2} - 96{A^2}\kappa \xi + 64{\xi ^2}} }}{4}} 。$ | (35) |
图11为阻尼比

|
图 11 不同激励幅值对装置隔振性能的影响比较图 Fig. 11 Comparison of effects of different excitation amplitude the vibration isolation performance of the five-spring QZS vibration isolator |
|
|
表 1 研究激励幅值对装置隔振性能影响时的系统参数取值 Tab.1 The parameter values studied when different excitation amplitude effects on the vibration isolation performance of the five-spring QZS vibration isolator |
随着激励幅值的增大,五弹簧装置的绝对力传递率会产生明显的变化。激励幅值越大,绝对力传递率的最大值越大。在较小的激励幅值影响下,五弹簧装置的隔振性能表现较好。
比较相同激励幅值的条件,在激励频率增大的过程中,五弹簧装置率先开始隔振,意味着其能够隔离更低频的振动;当激励频率大于五弹簧装置的向下跳跃频率时,五弹簧装置的绝对力传递率小于单个弹簧隔振系统,意味着其具有更好的隔振性能;在较高的激励频率区间,五弹簧装置的隔振性能优势逐渐减小。此外,对于五弹簧装置,随着激励幅值的增大,其隔振起始频率减小,因而为了获得更好的低频隔振性能,需要控制适当的激励幅值。
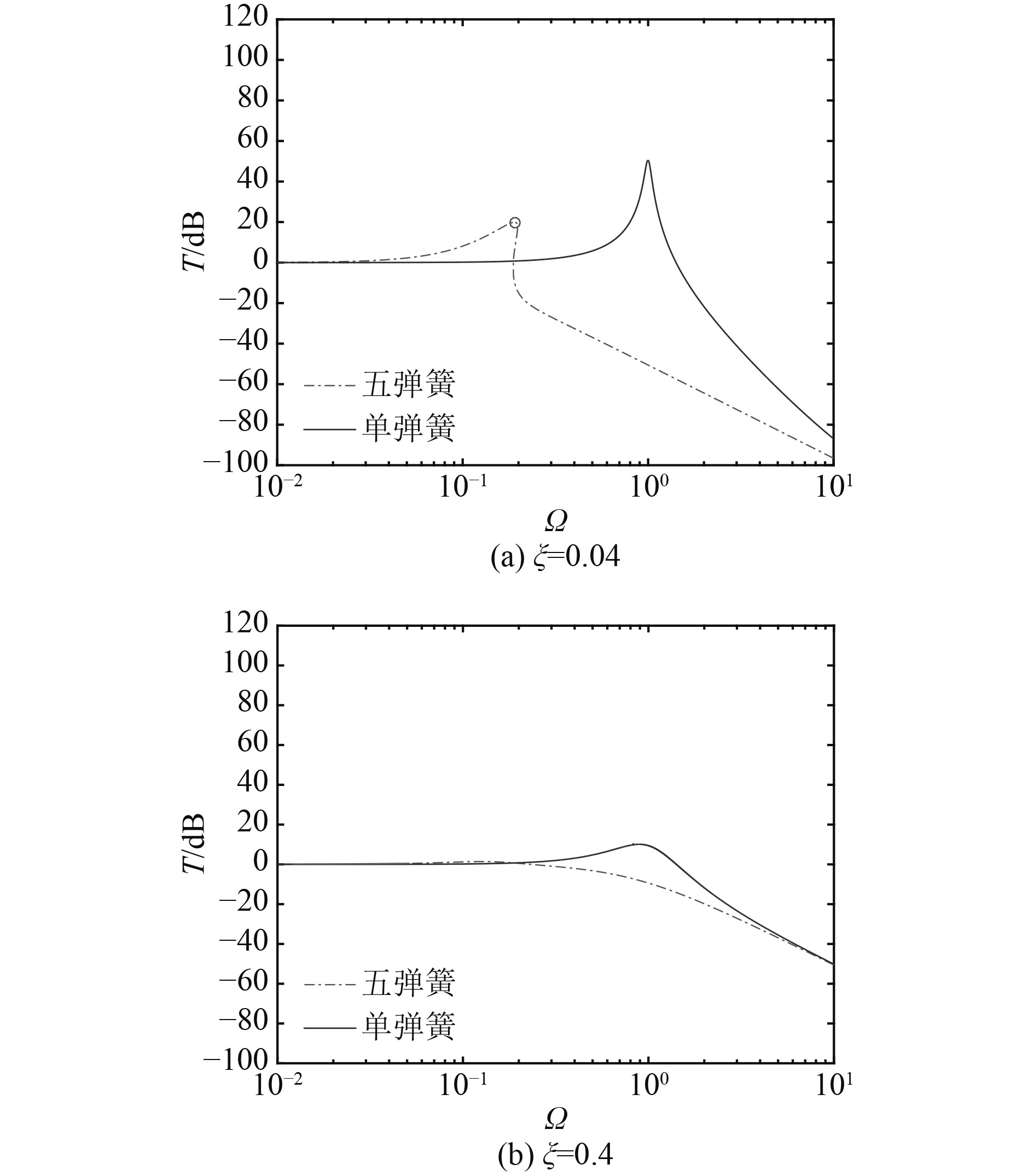
3.2.2 阻尼比的影响图12为激励幅值
|
图 12 不同阻尼比对装置隔振性能的影响比较图 Fig. 12 Comparison of effects of different damping ratio the vibration isolation performance of the five-spring QZS vibration isolator |
|
|
表 2 研究阻尼比对装置隔振性能影响时的参数取值 Tab.2 The parameter values studied when different damping ratio effects on the vibration isolation performance of the five-spring QZS vibration isolator |
随着阻尼比的增大,2个装置在不同激励频率区间内隔振性能的相互关系与激励幅值增大时正好相反。较大的阻尼比会使2个系统绝对力传递率的最大值均减小。当阻尼比增大到一定程度时,五弹簧装置的绝对力传递率的最大值消失。因而在调整五弹簧装置的隔振性能时,需选择适当的阻尼比。
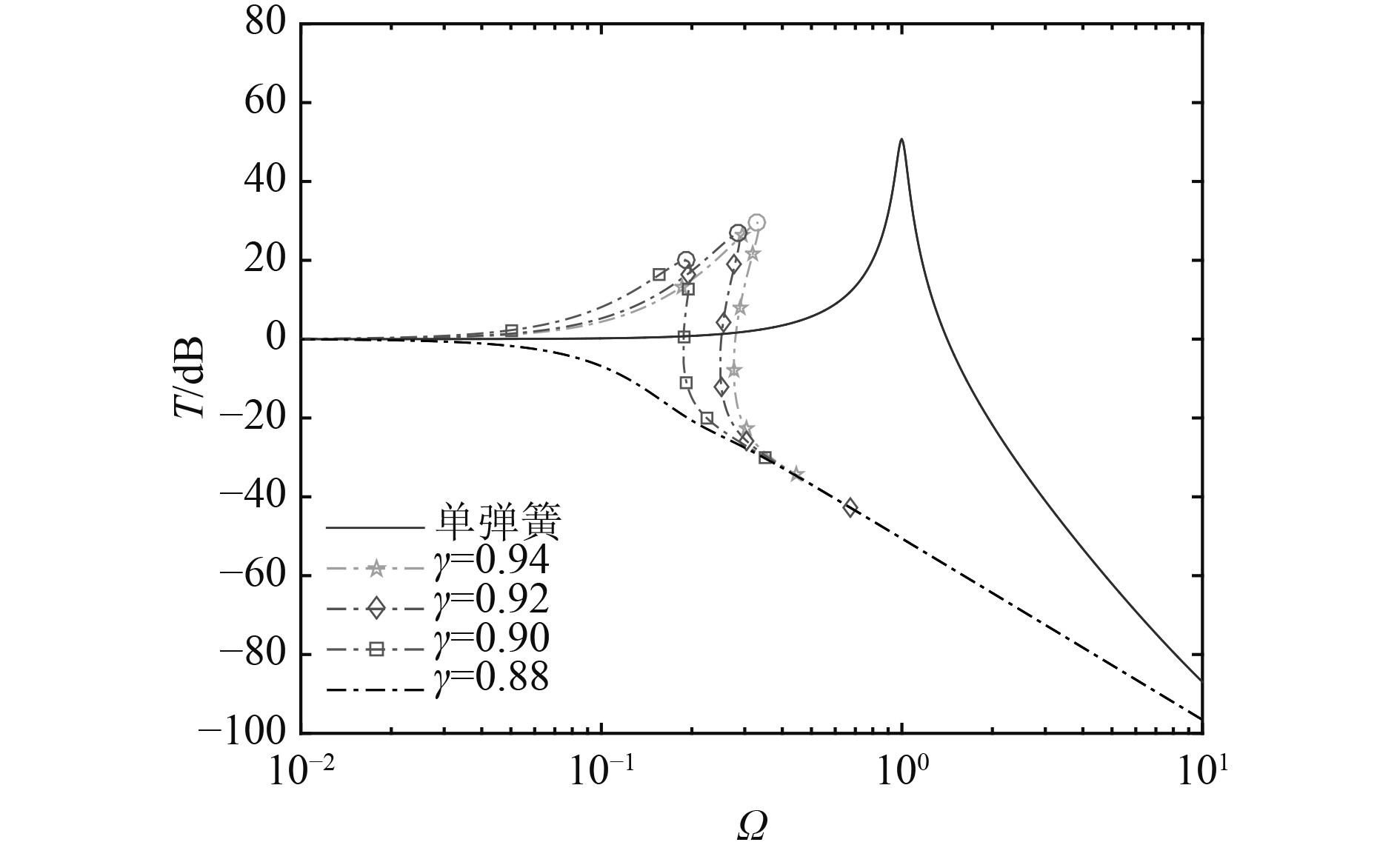
3.2.3 结构参数的影响图13与图14分别为激励幅值
|
图 13
不同
|

|
图 14
不同
|
|
|
表 3 研究
|
|
|
表 4 研究
|
当结构参数
当结构参数
对建立的五弹簧准零刚度隔振装置模型进行静力学推导,并在静力学分析的基础上对五弹簧装置的回复力进行泰勒展开并近似求解,利用谐波平衡法得到了五弹簧装置的动力学方程,研究不同参数对力传递率与跳跃频率的影响,得出如下结论:
1)五弹簧装置可以通过对参数
2)五弹簧装置的绝对力传递率会随着激励幅值的增大产生明显的变化。激励幅值越大,绝对力传递率的最大值越大;在较小的激励幅值影响下,五弹簧装置的隔振性能表现较好;相同激励幅值条件下,五弹簧装置率先开始隔振,能够隔离更低频的振动;当激励频率大于五弹簧装置的向下跳跃频率时,五弹簧装置的绝对力传递率小于单个弹簧隔振装置,具有更好的隔振性能;在较高的激励频率区间,五弹簧装置的隔振性能优势逐渐减小;控制适当的激励幅值能够使五弹簧装置获得更好的低频隔振性能。
3)较大的阻尼比会使2个隔振装置绝对力传递率的最大值均减小。当阻尼比增大到一定程度时,五弹簧装置绝对力传递率的最大值消失。因而在调整五弹簧装置的隔振性能时,需选择适当的阻尼比。
4)结构参数
5)当结构参数
总体来说,五弹簧装置平衡位置附近的低刚度范围更大,系统稳定性更好,有利于工程应用。
| [1] |
HARRIS C M, PIERSOL A G. Shock and vibration handbook[M]. McGraw-Hill, New York, 2002.
|
| [2] |
NAYFEH A H, MOOK D T. Nonlinear Oscillations[M]. Wiley, New York, 1979.
|
| [3] |
ALABUZHEV P, GRITCHIN A , KIM L, et al. Vibration protecting and measuring systems with Quasi-Zero stiffness, Hemisphere Publishing, New York, 1989.
|
| [4] |
KOVACICI, BRENNAN M J, WATERS T P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic[J]. Journal of Sound and Vibration, 2008, 315(3): 700-711. DOI:10.1016/j.jsv.2007.12.019 |
| [5] |
CARRELLA A, BRENNAN M J, KOVACIC I, et al. On the force transmissibility of a vibration isolator with quasi-zero-stiffness[J]. Journal of Sound and Vibration, 2009, 322(4-5): 707-717. DOI:10.1016/j.jsv.2008.11.034 |
| [6] |
BRENNAN M J, KOVACIC I, CARRELLA A, et al. On the jump-up and jump-down frequencies of the Duffing oscillator[J]. Journal of Sound and Vibration, 2008, 318(4-5): 1250-1261. DOI:10.1016/j.jsv.2008.04.032 |
| [7] |
彭献, 张施详. 一种准零刚度隔振系统的静力与线性动力特性分析[J]. 力学季刊, 2012, 33(3): 492-498. PENG Xian, ZHANG Shi-xiang. Static and linear dynamic characteristics analysis for a kind of vibration isolation system with Quasi-Zero-Stiffness[J]. Journal of Marine Sciences, 2012, 33(3): 492-498. DOI:10.3969/j.issn.0254-0053.2012.03.021 |
| [8] |
任旭东. 空气弹簧准零刚度隔振器的特性分析及应用研究[D]. 北京: 中国人民解放军军事医学科学院, 2017.
|
 2023, Vol. 45
2023, Vol. 45
