船舶的航行环境较为特殊,受航行环境影响,船舶的过度振动,容易出现众多的不良后果[1]。船舶常选取钢夹层板作为主船体建筑结构材料,钢板是新型的船体建筑结构材料,具有强度高、重量轻和刚性大的特点,在海洋工程领域和船舶领域中,得到广泛的应用。分析主船体建筑结构强度的变化[2-3],对于提升船舶的运行可靠性具有重要意义。船舶设计时,需要依据船舶设计规范中的板厚计算公式、波浪弯矩剪力计算公式等进行设计。伴随船舶市场需求的多样化发展,仅采用船舶设计规范上的计算公式,已经无法满足船体结构强度的设计需求[4]。采用有效的分析方法进行船体结构强度的研究,已经成为船舶设计领域的研究重点。
目前已有众多学者针对船舶建筑结构强度分析进行研究。吴卫国等[5]以某大型邮轮上层建筑舷侧局部结构为研究对象,针对该邮轮建筑构建了缩比模型。利用所构建的模型进行剪切强度的实验。通过实验明确了该大型邮轮在剪切载荷作用下,结构的屈曲失效模式以及极限承载能力。梅佳雪等[6]针对船体内部加筋板的极限强度进行研究,构建了加筋板的有限元模型,利用构建的有限元模型,分析结构的初始挠度对船体加筋板的极限强度存在直接的影响。以上都是针对船体建筑结构的屈曲失效模式和极限强度进行研究,但是由于仅采用有限元模型进行船体建筑结构分析,结构强度的分析结果不够全面。为此,构建主船体建筑结构强度分析的钢质模型,开展钢质模型的有限元分析研究,通过实验分析主船体建筑结构的强度变化,为提升船舶主体建筑的结构强度提供依据。
1 主船体建筑结构强度钢质模型实验方法 1.1 主船体建筑结构强度钢质模型基本方程将弹性力学的基本方程应用于主船体建筑结构强度钢质模型构建中。主船体建筑结构受到载荷作用时,利用正应力分量
| $ \sigma = {\left[ {\begin{array}{*{20}{c}} {{\sigma _x}}&{{\sigma _y}}&{{\sigma _z}}&{{\tau _{xy}}}&{{\tau _{xz}}}&{{\tau _{yz}}} \end{array}} \right]^{\rm{T}}} 。$ | (1) |
主船体建筑结构在受到载荷作用时,将形成位移,出现变形情况,即主船体建筑结构受载荷作用,将出现形状的改变与位置移动情况[7]。用
| $\delta = {\left[ {\begin{array}{*{20}{c}} u & v & w \end{array}} \right]^{\rm{T}}}。$ | (2) |
主船体建筑结构随机点应变分量矩阵为:
| $ \varepsilon = {\left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}} & {{\varepsilon _y}} & {{\varepsilon _z}} & {\begin{array}{*{20}{c}} {{\gamma _{xy}}} & {{\gamma _{yz}}} & {{\gamma _{xz}}} \end{array}} \end{array}} \right]^{\rm{T}}} 。$ | (3) |
式中:εx、εy与εz表示主船体建筑结构的正应变分量,γxy、γyz与γxz表示主船体建筑结构的剪应变分量。
主船体建筑结构强度分析属于三维分析问题,主船体建筑的弹性力学方程构建,主要包括以下内容:
1)平衡微分方程。
| $ \left\{ {\begin{aligned} &{\frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}} + X = 0} ,\\ & {\frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\sigma _y}}}{{\partial y}} + \frac{{\partial {\tau _{xy}}}}{{\partial z}} + Y = 0} ,\\ &{\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\sigma _z}}}{{\partial z}} + Z = 0} 。\end{aligned}} \right. $ | (4) |
2)物理方程。利用物理方程描述主船体建筑结构受到加载作用时,应力与应变之间关系表达式为:
| $ \sigma = {\boldsymbol{D}}\varepsilon。$ | (5) |
式中,
3)边界条件。若主船体建筑结构表面的力
| $ \left\{ {\begin{aligned} & {\overline {{X_v}} = {\sigma _x}a + {\tau _{yx}}m + {\tau _{zx}}n},\\ & {\overline {{Y_v}} = {\tau _{xy}}a + {\sigma _y}m + {\tau _{zy}}n} ,\\ & {\overline {{Z_v}} = {\tau _{xz}}a + {\tau _{yz}}m + {\sigma _z}n} 。\end{aligned}} \right. $ | (6) |
式中,
通过分析主船体建筑结构强度的几何相似关系,构建主船体建筑结构的钢质模型,进行主船体建筑的结构强度实验分析。主船体建筑结构的钢质模型主要研究主船体上层建筑结构,在受到不同载荷影响时的应力分布特征。所构建的主船体建筑结构的钢质模型,在结构上应满足主船体建筑的几何相似需求。为了分析主船体建筑结构的强度变化[7],实验过程中的载荷需要满足钢质模型的相似性准则。
为了保证利用钢质模型实验,获取与主船体建筑不同载荷工况时相同的应力水平分布,选取与主船体建筑相同的结构材料,构建钢模实验模型。选取主船体建筑结构钢制材料的杨氏模量
| $ \sigma ' = Mz/I。$ | (7) |
式中:
依据相似性理论,获取相同站位时主船体建筑与钢质模型剖面特性的相似性关系表达式如下:
| $ \left\{ {\begin{aligned} & {\frac{{{I_m}}}{{{I_s}}} = \lambda _L^{}\lambda _t^2},\\ & {\frac{{{z_{nm}}}}{{{z_{ns}}}} = 2{\lambda _L}} 。\end{aligned}} \right. $ | (8) |
式中:Is与Im分别表示主船体建筑结构与钢质模型的剖面垂向惯性矩,zns与znm分别表示主船体建筑结构与钢质模型的垂向中和轴高度。
为了保证主船体建筑结构受到加载时,相同位置形成相同的应力,对所构建的钢质模型施加的载荷Mm与主船体建筑结构实体受到的载荷Ms,应该满足如下条件:
| $ \frac{{{M_m}}}{{{M_s}}} = 2\lambda _L^{}\lambda _t^2。$ | (9) |
选取全船有限元分析方法,分析主船体建筑结构强度。利用主船体建筑结构强度钢质模型的有限元分析,明确主船体建筑结构的高应力区域,为主船体建筑结构强度分析提供基础。选取Ansys有限元分析软件构建主船体建筑的有限元模型。选取SESAM水动力分析软件,依据船舶航行区域的水域波浪等参数,模拟船舶航行过程中,可能受到的波浪等载荷。在所构建的主船体建筑结构强度钢模有限元分析模型中,施加货物载荷、设计波载荷等载荷,利用有限元软件的分析与求解,获取主船体建筑结构受到载荷作用时,不同部位的应力与变形情况,确定主船体建筑结构的强度变化情况。
1.3.1 分析主船体梁的载荷组成船舶运行时,受到海面作用漂浮在水面上,海面的波浪载荷、主船体自身的重力等力,直接作用于船体建筑上。依据船舶航行时,主船体在海浪作用下的漂浮状态,确定主船体的静水载荷。船舶运行时,海面环境波动性较强,主船体随机受到不同大小的波浪载荷。通过水动力分析方法分析主船体所在海域的波浪数据,确定主船体受到的波浪载荷。主船体建筑结构强度分析时,梁的载荷是分析建筑结构强度的重要前提。
1.3.2 构建主船体建筑全船结构的有限元模型通过构建主船体建筑全船结构的有限元模型,体现主船体建筑结构中梁的受力与变形情况。构建主船体建筑全船结构的有限元模型时,忽略甲板室与上层建筑结构。利用Ansys有限元分析软件构建主船体建筑结构钢模的有限元模型,各构件的模拟方式如表1所示。依据表1的结构构件模拟方法,构建主船体建筑结构强度钢模的有限元分析模型,进行主船体建筑结构的强度分析。
|
|
表 1 主船体建筑结构构件模拟 Tab.1 Simulation method of structural components of main hull building |
通过实验分析所构建主船体建筑结构强度钢质模型,是否能够有效分析主船体建筑结构强度变化。选取某船作为分析对象,该船主船体的参数如表2所示。
|
|
表 2 船体主要参数 Tab.2 Main parameters of the hull |
采用本文方法,利用Ansys有限元分析软件,构建该船的主船体建筑结构钢质模型的有限元模型。完成主船体单元划分后的有限元模型如图1所示。所构建的主船体有限元模型中包含85461个单元和68541个节点。

|
图 1 主船体有限元模型单元划分结果 Fig. 1 Result of element division of finite element model of main hull |
为主船体建筑结构有限元模型中的各单元赋予钢体材料属性,该船体的有限元模型构建结果如图2所示。

|
图 2 主船体有限元模型 Fig. 2 Finite element model of main hull |
对所构建的主船体建筑结构强度钢模有限元模型施加不同大小的载荷,主船体的应力分布如图3所示。可以看出,采用本文方法依据所构建的主船体建筑结构强度钢质模型,进行有限元分析,在施加载荷时,船体各部分的应力存在一定的变化。图3验证所构建的有限元模型,可以体现主船体建筑结构强度钢质模型的强度分析有效性。

|
图 3 主船体应力分布 Fig. 3 Stress distribution of main hull |
为主船体加载不同大小的载荷,统计主船体建筑应力最大值位置的应力变化,统计结果如图4所示。可以看出,伴随载荷不断增加,该处位置的应力不断变化。应力最大点位置位于船尾端的侧壁开口位置。加载载荷为300 t时,该点的应力达到了325.31 MPa,此时已经超过该材料的名义屈服应力。实验载荷加至150 t时,该测试点的应力变化呈现了非线性的变化特性。造成材料出现非线性特征的原因可能是,该测试点与材料焊缝的位置较近,因此实验载荷到达一定值时,主船体建筑结构材料焊缝附近释放了残余应力,导致测试点的结构应力出现明显的变化。
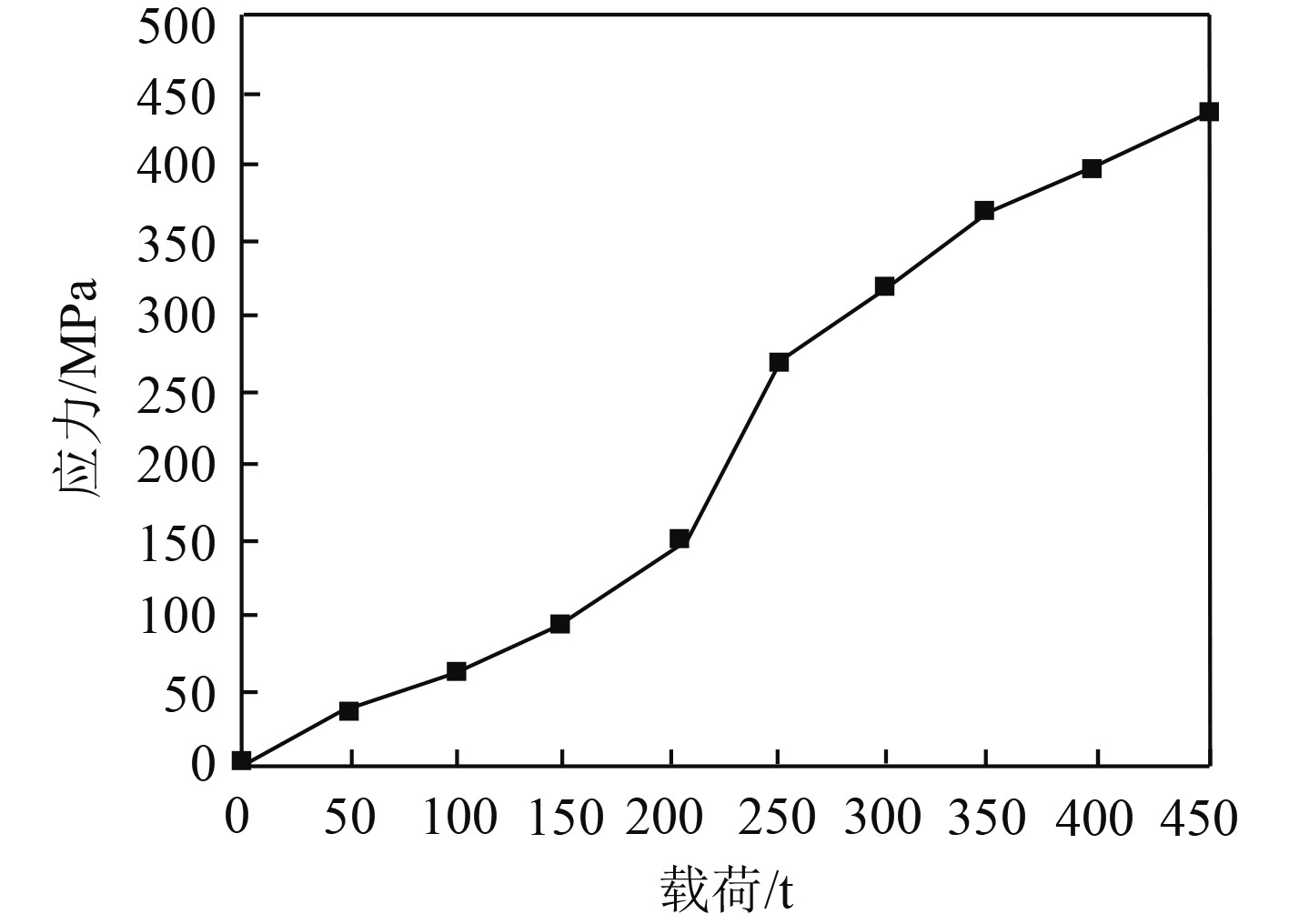
|
图 4 应力随载荷变化图 Fig. 4 Diagram of stress variation with load |
采用本文方法对主船体建筑结构中的某钢夹层板的应力进行钢模分析,该钢夹层板的厚度为15 mm。将本文方法构建的分析模型,与夹层板的实际应力对比,验证钢模对结构强度分析有效性,对比结果如表3所示。可以看出,采用本文方法构建的主船体建筑结构强度钢质模型,可以有效体现主船体建筑结构材料的强度变化。本文方法构建钢质模型分析主船体建筑结构材料强度的分析结果,与建筑结构材料的实际强度相差较小。实验结果验证,本文方法研究的主船体建筑结构强度钢质模型,具有较高的强度分析有效性,可以作为主船体建筑结构强度分析模型。利用该方法明确主船体建筑结构的受力情况,适用于不同类型的主船体建筑结构强度分析中。
|
|
表 3 钢夹层板强度分析结果 Tab.3 Strength analysis results of steel sandwich plate |
针对主船体建筑结构强度的精准分析需求,构建钢质模型,通过有限元分析模型,验证所构建的钢质模型分析主船体建筑结构强度的有效性。通过实验验证,所构建的钢质模型可以有效分析主船体的建筑结构强度,真实体现主船体建筑结构受到加载时的强度变化特性。所研究方法在船舶研究领域中,具有一定实用价值。
| [1] |
刘俊杰, 丁震, 马琳, 等. 总纵弯曲下舰船上层建筑结构强度钢模试验[J]. 中国舰船研究, 2022, 17(2): 135-141. DOI:10.19693/j.issn.1673-3185.02240 |
| [2] |
姚静, 郑建丽, 杨浩. 基于直接计算法的聚乙烯渔船船体结构强度研究[J]. 渔业现代化, 2023, 50(1): 89-96. DOI:10.3969/j.issn.1007-9580.2023.01.012 |
| [3] |
王一飞, 张乾坤, 李英伟. 大型邮轮船体结构总纵强度设计流程[J]. 船舶工程, 2022, 44(5): 12-16. |
| [4] |
曹万林, 张元, 边瑾靓, 等. 高空大悬挑主桁架式钢模架受力性能试验研究[J]. 建筑结构, 2021, 51(9): 120-127. DOI:10.19701/j.jzjg.2021.09.020 |
| [5] |
吴卫国, 胡灏天, 刘斌, 等. 大型邮轮上层建筑舷侧开口结构剪切强度试验研究[J]. 中国造船, 2021, 62(2): 25-32. DOI:10.3969/j.issn.1000-4882.2021.02.003 |
| [6] |
梅佳雪, 杜尊峰, 朱海涛. 船体结构加筋板极限强度的影响因素[J]. 船舶工程, 2021, 43(9): 37-42+64. DOI:10.13788/j.cnki.cbgc.2021.09.08 |
| [7] |
何丽丝, 曹荣, 王德禹. 面向送审的船体结构三维模型转化数据技术研究[J]. 中国舰船研究, 2021, 16(5): 206-215. DOI:10.19693/j.issn.1673-3185.01874 |
 2023, Vol. 45
2023, Vol. 45
