0 引　言

充液管道是舰船冷却系统、均衡系统、供油系统中的重要组成部件，承担着运输的功能。同时设备引起的管壁振动和管内的噪声也会沿着管路系统进行传递，从而影响舰船的水下声辐射性能。随着海水抗腐蚀性能和轻量化设计要求的提高，越来越多的先进复合材料结构被应用于管路系统的振动控制中。功能梯度材料(Functionally Graded Material, FGM)是在1984年由日本科学家提出的一种材料参数特性可随空间位置呈现连续梯度变化的新型材料，如线性或指数特性变化^[1]。此外由于具有很强的可设计特性、较好的耐磨损性能和抗断裂性能，功能梯度材料在工业领域有着极大应用前景^[2-3]。功能梯度管路是指管壳结构中，沿着管道的轴向分布有着不同的材料组分或结构设计，以实现不同功能。设计功能梯度管路时，材料组分和结构设计都非常重要。目前，常用的材料组分主要包括金属、陶瓷、聚合物以及它们的复合材料等。而结构设计包括管径、壁厚、弯曲角度、弯曲半径等因素。研究功能梯度管路的方向非常广泛，包括力学性能、热学性能，以及流体力学性能等。其中，流体力学性能是功能梯度管路的一个重要研究领域。研究表明，在功能梯度管路中，不同的材料组分和结构设计会对流体的传输性能产生显著影响，例如可降低流体的阻力，改善流体的流动状态等。在功能梯度管路的制备方面，常用的方法包括机械加工、热加工、化学合成等。其中，热加工是一种常见的方法，可通过热轧、热拉伸等方式实现功能梯度管路的制备。另外，化学合成也是一种常用方法，目前已有许多关于此方面的研究成果。总的来说，功能梯度管路已成为研究的热点之一，其研究涉及多个领域，包括材料科学、力学工程、流体力学等。

目前在船舶海洋工程中，冷却和输流等充液管道主要采用铜、铁等金属管道，随时间推移，海水极易对金属材料管壁造成腐蚀，形成管道内部堵塞，缩短了管道使用年限和增加了维护保养费用^[4]。当流体与管壁碰撞并挤压时，会引起耦合振动并进一步增加噪声。然而，传统金属材料的声学阻尼性能相对较差，这对舰艇的减震和降噪造成了相当大的不利影响。目前具有优良的抗疲劳、阻尼特性新型复合材料越来越多的被应用于工业中^[5]。本文考虑以功能梯度材料取代金属材料应用于输流管道，分析材料改变对于充液管道振动的影响。

一般来说，管道的轴向尺寸明显大于径向尺寸，充液管路理论模型中通常采用充液梁模型和充液圆柱壳2种理论模型。在早期的研究中，管内流体的影响仅仅被作为附加质量作用于充液梁的振动方程中，从而不考虑流体与管道之间的耦合效应^[6-8]。在随后的研究中，充液管道耦合理论得到了进一步发展，包括管壁材料引起的泊松耦合、弯管分支管等不连续处的连接耦合和管壁内部的摩擦耦合效应等。在理论模型完善上，William^[9]和Walker等^[10]首先考虑了管内流体在管道轴向的可压缩性。Wiggertr等^[11]和Lesmezr等^[12]则考虑了管壁材料的泊松耦合效应，即管壁轴向的应力波与管内流体声波之间的相互耦合作用。另外，Leer等^[13]还在理论中加入了重力作用和流体的粘性效应。此外，Gormanr等^[14]也考虑了管道的径向变形和初始预应力作用。考虑管路流固耦合(Fluid-Structure Interaction, FSI)将有助于提高管路计算精度，不考虑流固耦合将会导致管内流体压力计算结果偏低，管路结构强度计算结果偏高。精确的管路流固耦合计算模型将有助于管路系统的优化与设计，而不够精确的计算结果则会导致管路失效，引发安全事故与经济损失。因此很多学者对管路流固耦合模型开展研究，管路流固耦合可看作是经典水锤理论的扩展，充液管路流固耦合从基本的2方程水锤模型发展到求解三维管路流固耦合振动的14方程模型，还经历了轴向振动4方程模型，横向振动6方程模型和面内振动8方程模型等逐渐完善的阶段。主要分为时域响应求解和频域响应求解两大类，时域分析方法以特征线法为代表，频域分析方法主要有传递矩阵法、阻抗综合法、动刚度法等。其中，传递矩阵法在求解长距离输流管道时会存在数值溢出和响应计算不稳定。

此外，稳定性分析也是充液管路重要的研究方向之一，Païdoussis等^[24]进行了大量的管路颤振和发散失稳方面的研究，Li等^[25]基于哈密尔顿原理研究了两端弹性约束充液管非线性振动特性，Djondjorov等^[26]研究了弹性基础上管路中流速对充液管道失稳特性的研究。但失稳管路中的流速都比较高，船舶充液管路流速通常为3～10 m/s。张涛等^[27]通过计算与实验研究发现，管内流速从0 m/s增加到8.9 m/s时，管路系统固有频率几乎不变。

目前，针对功能梯度管道流固耦合振动研究的文献较为有限。刘辰^[19]分别采用Euler梁和Timoshenko梁模型研究了功能梯度输流管的振动及失稳，此外近年来在微尺度方向对于单壁、多壁输流碳纳米管^[20-22]的研究也很热门，但大多将流体视为附加质量，并未考虑流体与结构的耦合。

本文假设管道材料特性沿管壁厚度方向呈现梯度变化。为了模拟管壁的连续梯度变化，将其均分为多层，并把每一层近似为均匀材料。基于管道流固耦合理论，将流速和压力设为变量，计入流体在管道轴向的可压缩性。通过管道的运动方程及流体运动、连续方程得出输流弯管的耦合振动方程，还可进一步退化为直管方程。采用动刚度法进行数值求解，并基于单位内控制方程的精确解进行计算。相较于有限元法，该方法具有更高的计算效率。

1 功能梯度充液管道控制方程 1.1 功能梯度管理论模型

假设管道截面为标准圆形，管道的径向坐标记为r，其内径为r₁，外径为r₂。又假设杨氏模量、密度以及泊松比都沿着半径厚度方向呈指数变化。如图1所示，将截面均匀地分为K层，并假设每一层的材料属性保持不变，同时沿厚度方向，层与层之间的材料参数呈现梯度变化例如第m层的材料参数表达式为：

$ \begin{split} & {E_m} = {E_1} + \left( {{E_2} - {E_1}} \right){\left( {\frac{{\dfrac{{{r_{m1}} + {r_{m2}}}}{2} - {r_1}}}{{{r_2} - {r_1}}}} \right)^n}，\\ & {\mu _m} = {\mu _1} + \left( {{\mu _2} - {\mu _1}} \right){\left( {\frac{{\dfrac{{{r_{m1}} + {r_{m2}}}}{2} - {r_1}}}{{{r_2} - {r_1}}}} \right)^n} ，\\ & {\rho _m} = {\rho _1} + \left( {{\rho _2} - {\rho _1}} \right){\left( {\frac{{\dfrac{{{r_{m1}} + {r_{m2}}}}{2} - {r_1}}}{{{r_2} - {r_1}}}} \right)^n}。\end{split} $

(1)

式中，下标1和下标2分别表示内界面和外界面的材料参数，r_m1和r_m2分别为第m层的内外半径，n为可变化的梯度指数。

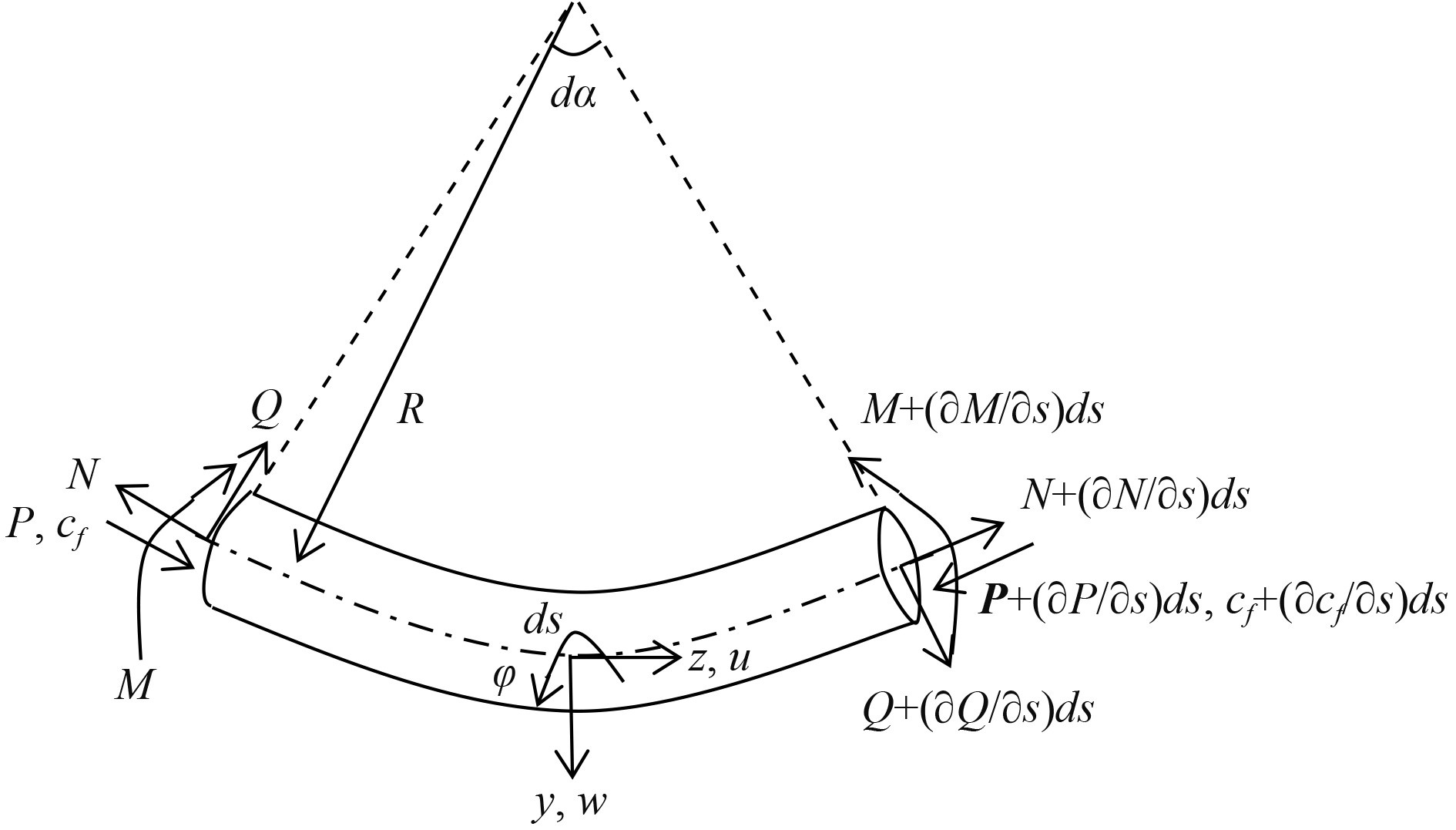
1.2 充液弯管方程

弯管是管路系统中的重要组成部件之一，具有改变管内流体流动方向功能。研究一段圆弧形充液弯管的振动，弯曲半径为R，弯曲角度为α，管道内半径为a，壁厚为e。图2为弯管的微元段，图中建立的局部坐标系沿管道的轴向弧线方向为s，面内与s方向相切的方向为z轴，垂直方向为y轴。弯管可视为一个曲梁结构，u和w分别表示梁的中性轴沿z轴和y轴的位移，φ表示面内的转角。在弯管两端截面上，N和Q分别表示轴向力和剪力，M表示弯矩，P和c_f表示流体截面的平均流体压力和流速。

对于曲梁结构，截面上的应变为：

$ {\varepsilon _0} = \frac{{\partial u}}{{\partial s}} + \frac{w}{R} ，\kappa = \frac{{\partial \varphi }}{{\partial s}} ，\gamma = \frac{{\partial w}}{{\partial s}} + \varphi - \frac{u}{R}。$

(2)

式中：κ 为曲率变化，ε₀ 为中性面上的应变，γ 为剪应变，则梁上任意一点轴向应变为 $ {\varepsilon _z} = {\varepsilon _0} + y\kappa $ 。

在y-z平面内，由图2可得该弯管横向及轴向的平衡方程为：

$ \begin{split} & \frac{{\partial Q}}{{\partial s}} - \frac{N}{R}{\text{ + }}\frac{{P{A_f}}}{R} - \left( {{\rho _f}{A_f} + {I_1}} \right)\frac{{{\partial ^2}w}}{{\partial {t^2}}} = 0，\\ & \frac{{\partial M}}{{\partial s}} + Q - {I_3}\frac{{{\partial ^2}\varphi }}{{\partial {t^2}}} = 0，\end{split} $

(3)

$ \frac{{\partial N}}{{\partial s}} + \frac{Q}{R} - {I_1}\frac{{{\partial ^2}u}}{{\partial {t^2}}} = 0 。$

(4)

式中：ρ_f为流体密度；A_f为流体截面积； ${I_1} = \sum\limits_{m = 1}^K {\rho _m}{\text{π }} \left( {{r_{m2}}^2 - {r_{m1}}^2} \right)$ ； ${I_3} = \sum\limits_{m = 1}^K {{\rho _m}\frac{{\text{π}} }{4}\left( {{r_{m2}}^4 - {r_{m1}}^4} \right)}$ ，分别表示单位长度功能梯度管道的质量和转动惯量。

流体在轴向的运动方程和连续方程为：

$ \frac{{\partial P}}{{\partial s}} + {\rho _f}\frac{{\partial {c_f}}}{{\partial t}} = 0，$

(5)

$ \mathop{\oiiint}\limits_{{V_c}} {\left[ {\frac{{\partial {\rho _f}}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}{{\vec v}_f}} \right)} \right]} {\rm{d}}{V_c} = 0。$

(6)

式中：V_c为管内流体控制微元，v_f为管道内任意一点处的流速，显然方程 $\dfrac{{\partial {\rho _f}}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}{{\vec V}_f}} \right) = 0$ 应对于控制体中的每一点都成立，引入流体状态方程及管道内平面波假设，连续方程可进一步化为：

$ \frac{1}{{{K_f}}}\frac{{\partial p}}{{\partial t}} + \frac{{\partial {v_f}}}{{\partial s}} + \frac{{{\partial ^2}{u_r}}}{{\partial r\partial t}} + \frac{1}{r}\frac{{\partial {u_r}}}{{\partial t}} + \frac{1}{R}\frac{{\partial w}}{{\partial t}} = 0 。$

(7)

式中：r为截面径向坐标；K_f为流体的体积模量；u_r为径向位移。在流体截面内进行积分并取平均值：

$ \frac{1}{{{K_f}}}\frac{{\partial P}}{{\partial t}} + \frac{{\partial {c_f}}}{{\partial s}} + \frac{1}{R}\frac{{\partial w}}{{\partial t}} + \frac{2}{a}{\left. {\frac{{\partial {u_r}}}{{\partial t}}} \right|_{r = a}} = 0 。$

(8)

而对于管壁结构中，每一层均满足本构方程：

$ {\varepsilon _z} = \frac{1}{{{E_m}}}\left[ {{\sigma _z} - {\mu _m}\left( {{\sigma _\theta } + {\sigma _r}} \right)} \right] {\varepsilon _\theta } = \frac{1}{{{E_m}}}\left[ {{\sigma _\theta } - {\mu _m}\left( {{\sigma _z} + {\sigma _r}} \right)} \right] 。$

(9)

式(9)可合并为：

$ {\varepsilon _\theta } = \frac{{1 - \mu _m^2}}{{{E_m}}}\left( {{\sigma _\theta } - \frac{{{\mu _m}}}{{1 - {\mu _m}}}{\sigma _r}} \right) - {\mu _m}{\varepsilon _z} 。$

(10)

在圆环截面上 ${\varepsilon _\theta } = \dfrac{{{u_r}}}{r}$ ，且假设由流体压力引起的管道截面上周向应力均匀分布，径向应力沿半径方向线性分布：

$ {\sigma _\theta } = \frac{{Pa}}{e}，{\sigma _r} = \frac{{r - a - e}}{e}P 。$

(11)

将式(10)沿管壁截面积分，取平均值得：

$ \frac{{{{\bar u}_r}}}{a} = XP - \bar \mu \left( {\frac{{\partial \bar u}}{{\partial s}} + \frac{{\bar w}}{R}} \right) 。$

(12)

式中：X为与材料参数相关的常系数， ${{X = \frac{{\displaystyle\sum {\dfrac{{1 - {\mu _m}^2}}{{{E_m}}}\left[ {{A_m}a - \dfrac{{{\mu _m}}}{{1 - {\mu _m}}}\left( {\dfrac{{2\pi }}{3}\left( {{r_{m2}}^3 - {r_{m1}}^3} \right) - (a + e){A_m}} \right)} \right]} }}{{{A_p}e}}}}$ ，上划线表示管道截面的平均值，A_p 为管道截面积，A_m为第m层的面积。对于薄壁管道而言，截面内径向和轴向的位移都取为平均值，因此将式(12)代入式(8)，得到：

$ \begin{aligned}\left( {\frac{1}{{{K_f}}} + 2X} \right)\frac{{\partial P}}{{\partial t}} + \frac{{\partial {c_f}}}{{\partial s}} - 2\bar \mu \frac{{{\partial ^2}u}}{{\partial s\partial t}} + \left( {1 - 2\bar \mu } \right)\frac{1}{R}\frac{{\partial w}}{{\partial t}} = 0。\end{aligned}$

(13)

内力由应力在管道截面上的积分得到：

$ Q = {k_s}\int_{{A_p}} {\tau {\rm{d}}A = {k_s}} \sum {\frac{{{E_m}{A_m}}}{{2\left( {1 + {\mu _m}} \right)}}} \left( {\frac{{\partial w}}{{\partial s}} + \varphi - \frac{u}{R}} \right)，$

(14)

$ M = \int_{{A_p}} {{\sigma _z}y{\rm{d}}A} = \sum {{E_m}\frac{{\text{π}} }{4}\left( {{r_{m2}}^4 - {r_{m1}}^4} \right)} \frac{{\partial \varphi }}{{\partial s}}，$

(15)

$ N = \int_{{A_p}} {{\sigma _z}{\rm{d}}A} = \sum {{E_m}{A_m}\left( {\frac{{\partial u}}{{\partial s}} + \frac{w}{R}} \right) + {\mu _m}P\left[ {\frac{{2\pi }}{{3e}}\left( {{r_{m2}}^3 - {r_{m1}}^3} \right) - {A_{_m}}} \right]} 。$

(16)

式中：k_s 为剪切系数，对于圆形截面梁来说， ${k_s} = \dfrac{{6\left( {1 + \mu } \right){{\left( {1 + \beta } \right)}^2}}}{{\left( {7 + 6\mu } \right){{\left( {1{\text{ + }}\beta } \right)}^2}{\text{ + }}\left( {20{\text{ + }}12\mu } \right){\beta ^2}}}$ ；μ 为截面上泊松比的平均值；β 为内外半径的比值。在各向同性均匀材料的管道中，相同材料下，弯管的刚度小于直管刚度，因此弯曲刚度要除以弯曲因子ff。以此类推，对于本文研究的功能梯度管道，在式(15)中引入弯曲因子的影响 $M = \dfrac{{\displaystyle\sum {{E_m}\frac{{\text{π}}}{4}\left( {{r_{m2}}^4 - {r_{m1}}^4} \right)} }}{{ff}}\dfrac{{\partial \varphi }}{{\partial s}}$ ，一般工程中常用的弯管弯曲半径大，截面尺寸小，借鉴经验公式取 $f f = 1.65{a^2}/eR$ 。

方程(3)～方程(5)、方程(13)～方程(16)构成了功能梯度充液弯管的面内振动方程。

2 管系振动求解

采用管道子结构的刚度矩阵为最小的拼接单元，为了在同一矩阵下组装管道，采用管道两端的流体位移变量，需从管道振动控制方程中的变量速度进行偏导变化求得。根据分离变量原则，假设管道两端的位移和力变量形式为： $ \psi \left( {s,t} \right) = \Psi \left( s \right){e^{i\omega t}} $ 。其中，i为虚数单位(i²=-1)，ω为圆频率。联立方程，消去振动控制方程中的内力变量，则得到关于位移变量的矩阵方程为：

$ {\boldsymbol{{ H}W = 0}}。$

(17)

其中，位移列向量为 ${\boldsymbol{W}} = {\left[ {u w \varphi d} \right]^{\rm{T}}}$ , H 为八阶微分矩阵。当H的行列式值为0时，可得8个特征根为 $ {\lambda _1} \sim {\lambda _8} $ 。假设其中一个变量φ的函数形式为 $\varphi = \sum\limits_{j = 1}^8 {{C_j}{e^{ - i{\lambda _j}s}}{e^{i\omega t}}}$ ，表达式中 $ {C_1} \sim {C_8} $ 为未知常数。利用方程(17)中任意3个等式，可求解出其他位移变量与φ之间的线性关系。

$ \begin{split} & u = \sum\limits_{j = 1}^8 {H{u_j}{C_j}} {e^{ - i{\lambda _j}s}}{e^{i\omega t}}，\quad w = \sum\limits_{j = 1}^8 {H{w_j}{C_j}} {e^{ - i{\lambda _j}s}}{e^{i\omega t}}，\\ & d = \sum\limits_{j = 1}^8 {H{v_j}{C_j}} {e^{ - i{\lambda _j}s}}{e^{i\omega t}}。\end{split} $

式中，Hu_j、Hw_j、Hv_j 均为常系数。联立式(13)～式(16)中的内力与位移之间的关系，可以用位移变量来表示内力变量。

每个管道单元都有首尾两端，将每一端的位移、转角和流速作为单元节点位移，将界面上的内力和流体压力作为单元节点外力。值得注意的是，位移和外力的函数都与 $ {C_1} \sim {C_8} $ 相关，因此节点外力和节点位移可用矩阵形式表示为：

$ {{\boldsymbol{D}}_{\boldsymbol{e}}}{\boldsymbol{ = }}{{\boldsymbol{K}}_{\boldsymbol{1}}}{\boldsymbol{C}}，{{\boldsymbol{F}}_{\boldsymbol{e}}}{\boldsymbol{ = }}{{\boldsymbol{K}}_{\boldsymbol{2}}}{\boldsymbol{C}}，$

(18)

$ \begin{split} &{{\boldsymbol{D}}_{\mathbf{e}}} = \left[ {u\left( 0 \right) w\left( 0 \right) \varphi \left( 0 \right) d\left( 0 \right) u\left( {R\alpha } \right) w\left( {R\alpha } \right) \varphi \left( {R\alpha } \right) d\left( {R\alpha } \right) } \right] \text{，}\\ & {{\boldsymbol{F}}_{\mathbf{e}}} = \left[ - N\left( 0 \right) - Q\left( 0 \right) - M\left( 0 \right) - P\left( 0 \right) N\left( {R\alpha } \right) Q\left( {R\alpha } \right) \right.\\ & \left. M\left( {R\alpha } \right) P\left( {R\alpha } \right) \right]。\end{split} $

式中：K₁ 和K₂ 为与ω相关的系数矩阵，Rα表示曲管的弧长。若管道为直管，则用管道长度L来代替Rα。

因此由式(18)可得节点力与节点位移的关系为：

$ {{\boldsymbol{F}}_{\boldsymbol{e}}}{\boldsymbol{ = }}{{\boldsymbol{K}}_{\boldsymbol{e}}}{{\boldsymbol{D}}_{\boldsymbol{e}}} 。$

(19)

其中，K_e 为单元动刚度矩阵， ${{\boldsymbol{K}}_{\boldsymbol{e}}}{\boldsymbol{ = }}{{\boldsymbol{K}}_{\boldsymbol{2}}}{{\boldsymbol{K}}_{\boldsymbol{1}}}^{{\boldsymbol{ - 1}}}$ 。

3 算例分析与讨论 3.1 退化至各向同性材料的验证

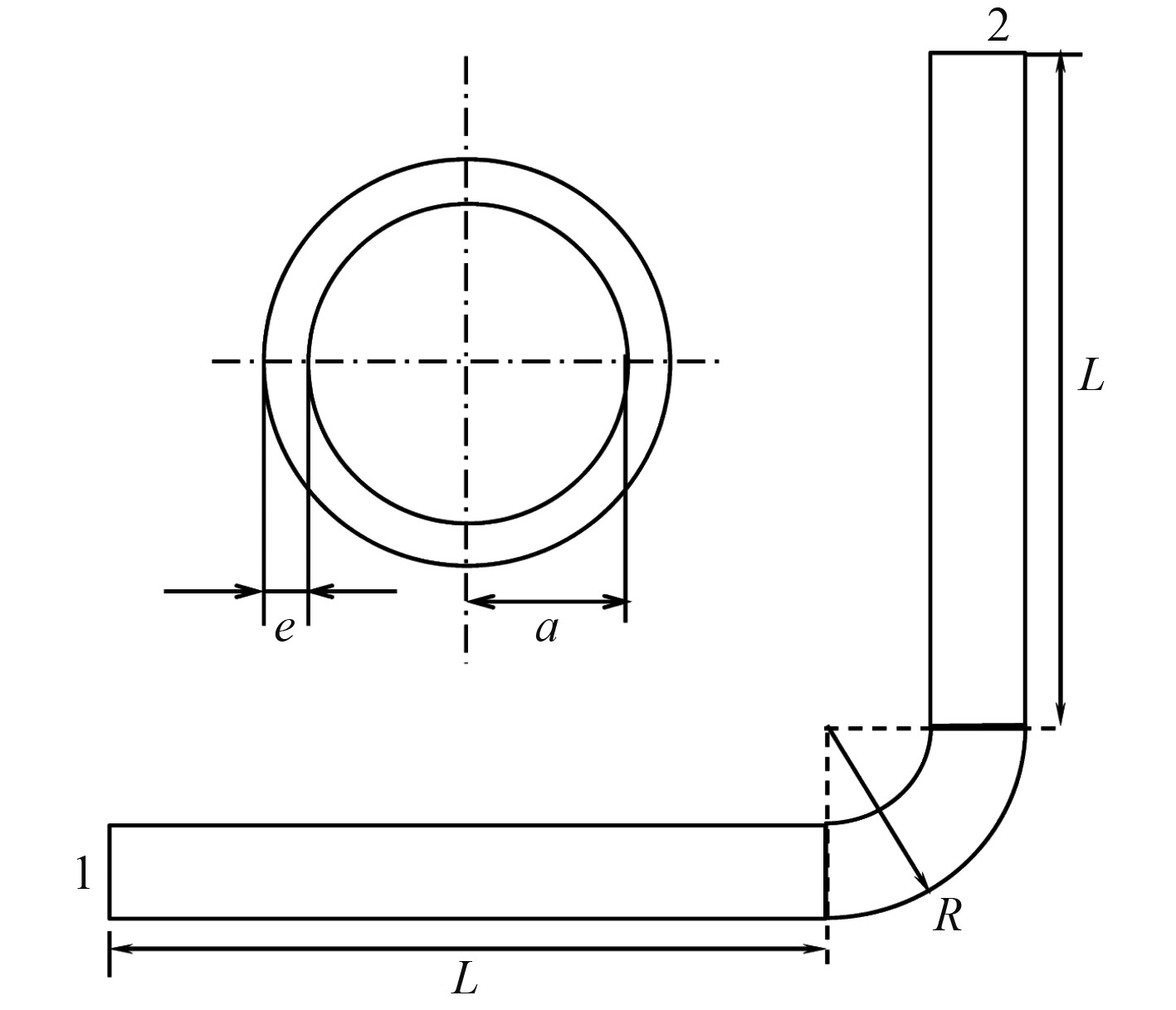
运用动刚度法计算图3中一段L型的空心管道，其一端固支，另一端自由。在自由端施加横向单位载荷时，该位置的1～1 000 Hz横向位移响应曲线如图4所示。离散模型是由若干条直管单元组装而成，同时在转角处会被离散成2段直管。而连续模型则由首末端的直管单元和一个弯曲单元组装而成，其中弯曲单元会被建模为梁模型，并且在有限元软件中进行计算。计算模型的尺寸及参数为：L=1 m；R=0.2 m；a=35 mm；e=5 mm；E=157 GPa；μ=0.34；ρ=9 000 kg/m³。从图4曲线可以看出，连续模型和离散模型计算结果非常接近。在低频范围内，有限元计算结果和动刚度法计算结果完全一致，而当频率升高，有限元网格划分细化度越高，越逼近动刚度法的计算曲线。由此可见本文采用的动刚度法计算效率相对较高。

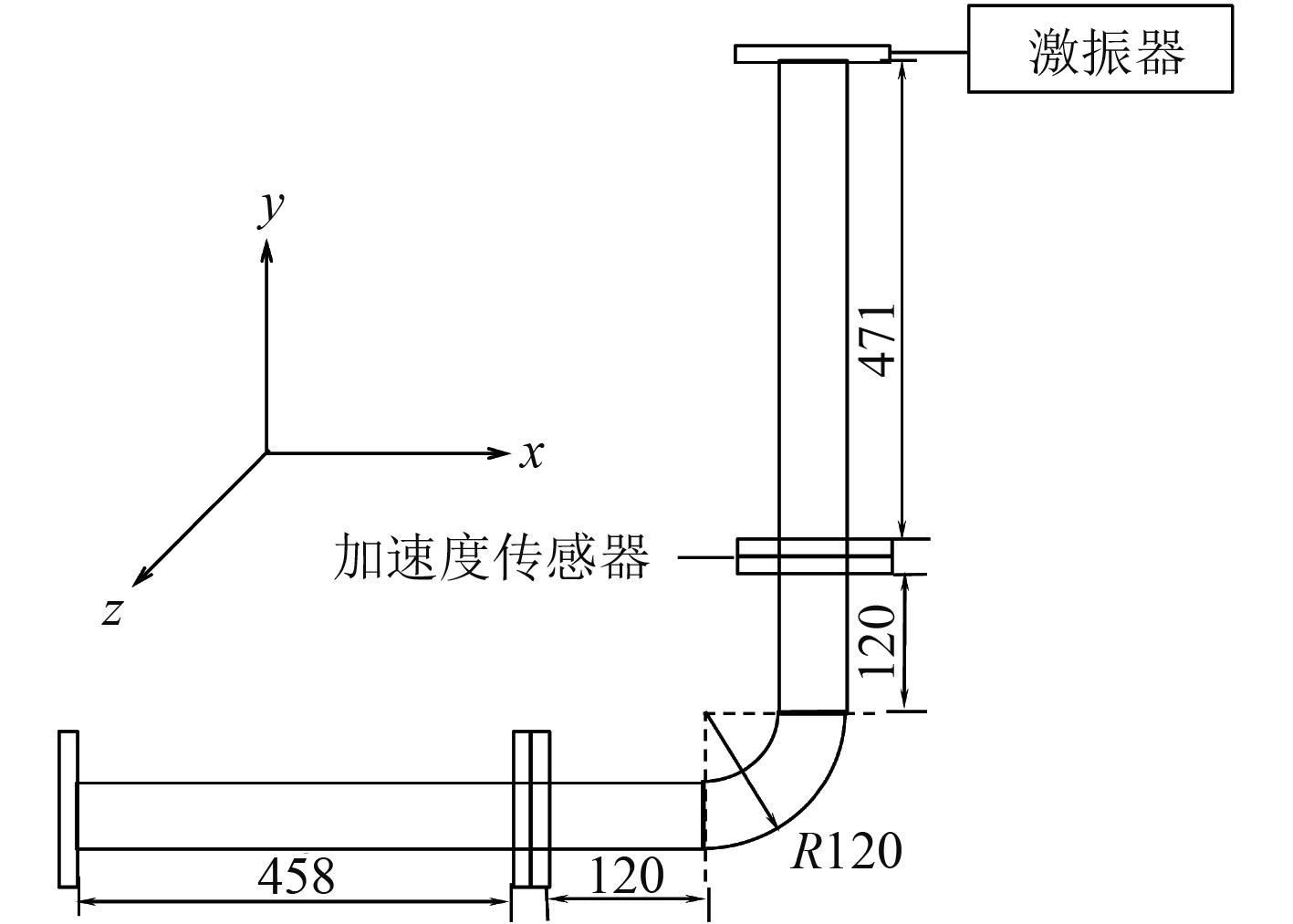
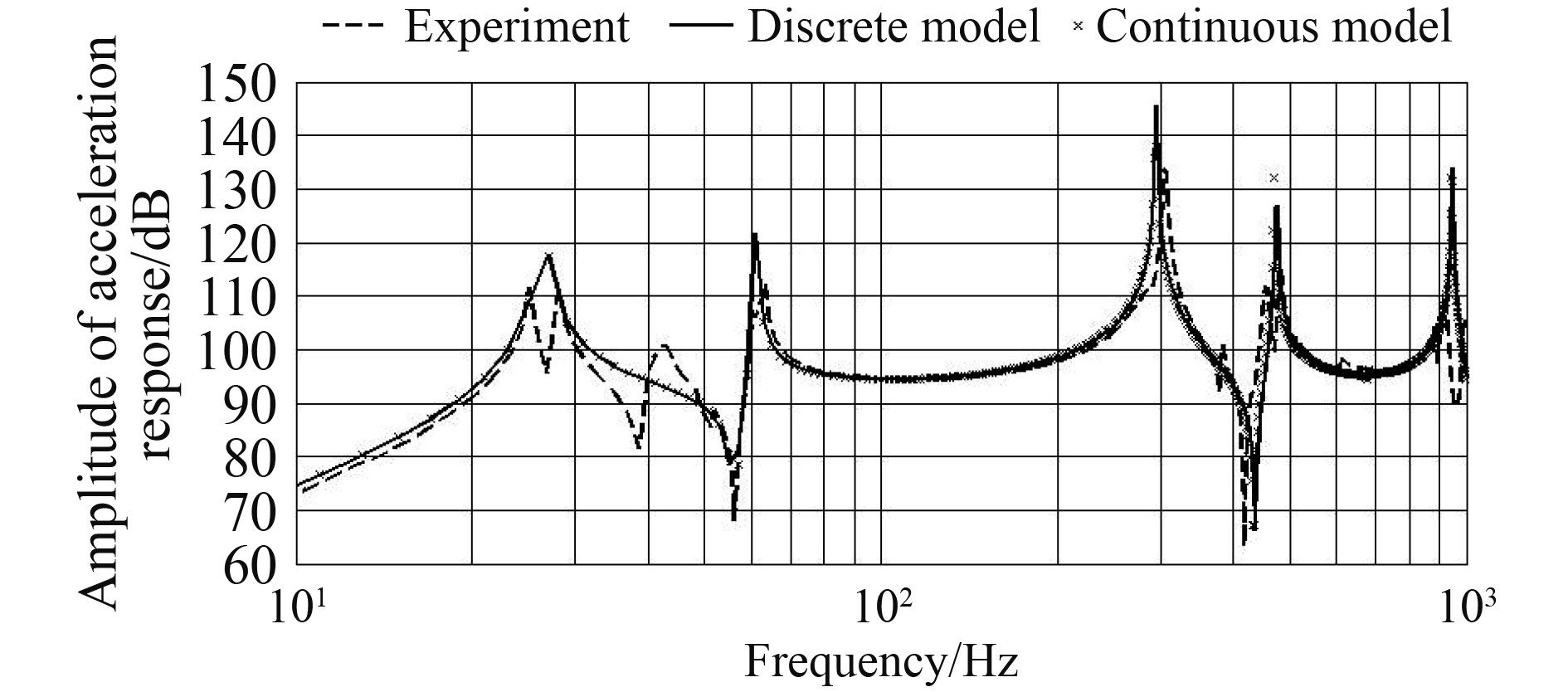
验证充液管道的振动特性。如图5所示，管道由一段带法兰的直管和一段弯曲管道构成。其中，管道左侧与管道支撑构件固定，管道上端无约束且与大气相通。管道材料密度为7 900 kg/m³，材料损耗为0.001，杨氏模量为210 GPa，泊松比为0.3。法兰内径为90 mm，外径为185 mm，厚度为20 mm，法兰与法兰之间通过螺栓连接。管道截面直径为80 mm，壁厚为4.5 mm，。管道内充液体为水，密度为1 000 kg/m³，体积模量为1.95 GPa，损耗为0.002。实验中，在管道的自由端放置了激振器，以产生单元力载荷，并进一步产生面内横向载荷。图6对比了10～1 000 Hz频率范围内的弯管面内振动加速度响应，实验结果表明理论预测与实验曲线吻合度较高。此外，对于内径较小的充液管路弯管而言，使用连续模型和离散模型的差异仍然较小。

3.2 功能梯度充液管道的振动

以一段长度为6 m、两端简支的功能梯度充液直管为例，其截面内径为0.2 m，内壁由SiC陶瓷材料制成，外壁由铝-SiC陶瓷材料复合而成。其中，SiC陶瓷的杨氏模量为427 GPa，泊松比为0.17，密度为3 100 kg/m³，铝-SiC陶瓷的杨氏模量为70 GPa，泊松比为0.33，密度为2 700 kg/m³，管内流体为水。管壁用20层均匀离散单元进行模拟，根据计算结果生成固有频率表。

表2列举的分别为前3阶弯曲模态，第一阶轴向模态及前3阶流体模态，由表中数据对比可见，管壁材料的变化对于结构模态的影响要大于对于流体模态的影响；管道截面壁厚与内径比越小，即管壁越薄，材料对于流体模态的影响越大；随n值增大，固有频率增大，但变化幅度逐渐变小。不过这是由沿壁厚方向的变化函数决定的。

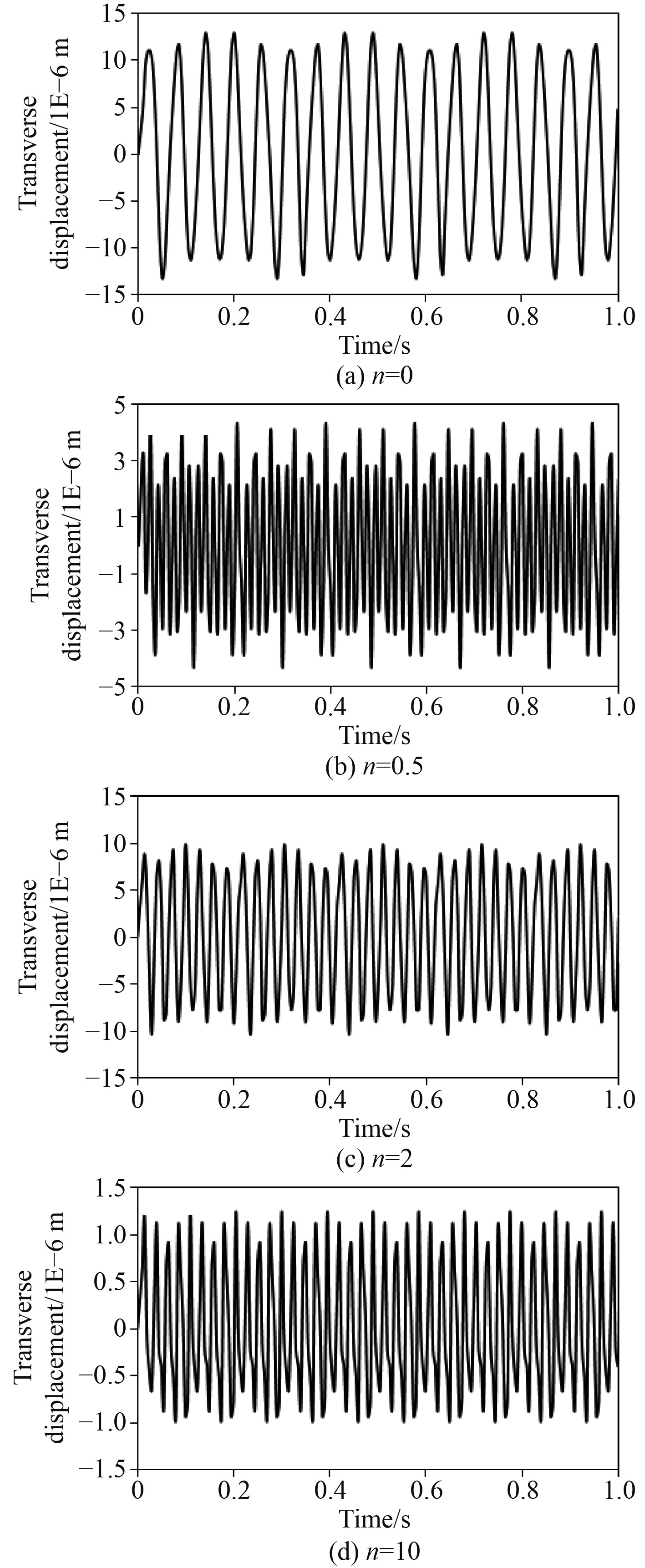
针对图3的管系算例，将金属材料变为功能梯度材料，在第一段直管末端施加横向单位载荷，得到频域内管道自由端的横向位移响应后，进行傅里叶逆变换得到时域内响应。图7展示了在0～1 s内，当采用不同n值的管道材料时，横向位移响应曲线的变化。值得注意的是，尽管在前面算例中发现n值升高能提高固有频率，但管道的振动幅值并非随n值的增大单调降低。选取几个具有代表性n值的计算结果。由图可知，在n值小幅提升时，振动幅值明显降低，但n值继续增大至3时，振动幅值反而增大，而当n进一步增大，即材料无限近似于内壁材料时，振动幅值又显著降低。由此可见，在工程中在应用功能梯度材料时，对于梯度变化函数的定义应综合考虑其动态特性和对结构的影响等因素。

4 结　语

本文研究了充液功能梯度管道的振动特性，将动刚度法应用于管道单元组装和拼接。通过与有限元和实验结果的对比验证，本文所采用的计算方法经证实准确可靠。由功能梯度管道的振动模态和时域响应分析可见：管道材料的变化对于结构的影响远大于对于流体的影响，管壁越薄，流体所受的影响越大；管壁应用功能梯度材料在保证强度和耐腐蚀的前提下，适当改变梯度指数能有效提高管道结构振动的稳定性，但梯度指数的选取与功能梯度材料本身的材料属性变化函数相关。本文提出的分层模型还可适用于多层复合管道，运用的动刚度法可适用于多种管道组装方式，且具有较高的计算效率。