0 引　言

为了抵御深水压力，潜艇耐压壳体通常被设计为柱锥结构形式，其横截面为圆形，而耐压壳体在建造、装配以及焊接过程中都会导致该截面偏离纯圆^[1-4]。因此，潜艇耐压壳体圆度评定的研究对控制其建造精度及潜艇安全性都具有重大意义。目前这类大型结构的圆度检测常采用全站仪等现代测量仪器，采集各肋骨剖面圆周上16或32等分点坐标或到中心线的距离，然后利用最小二乘法进行圆拟合，来评定耐压壳体是否满足要求^[5-7]。

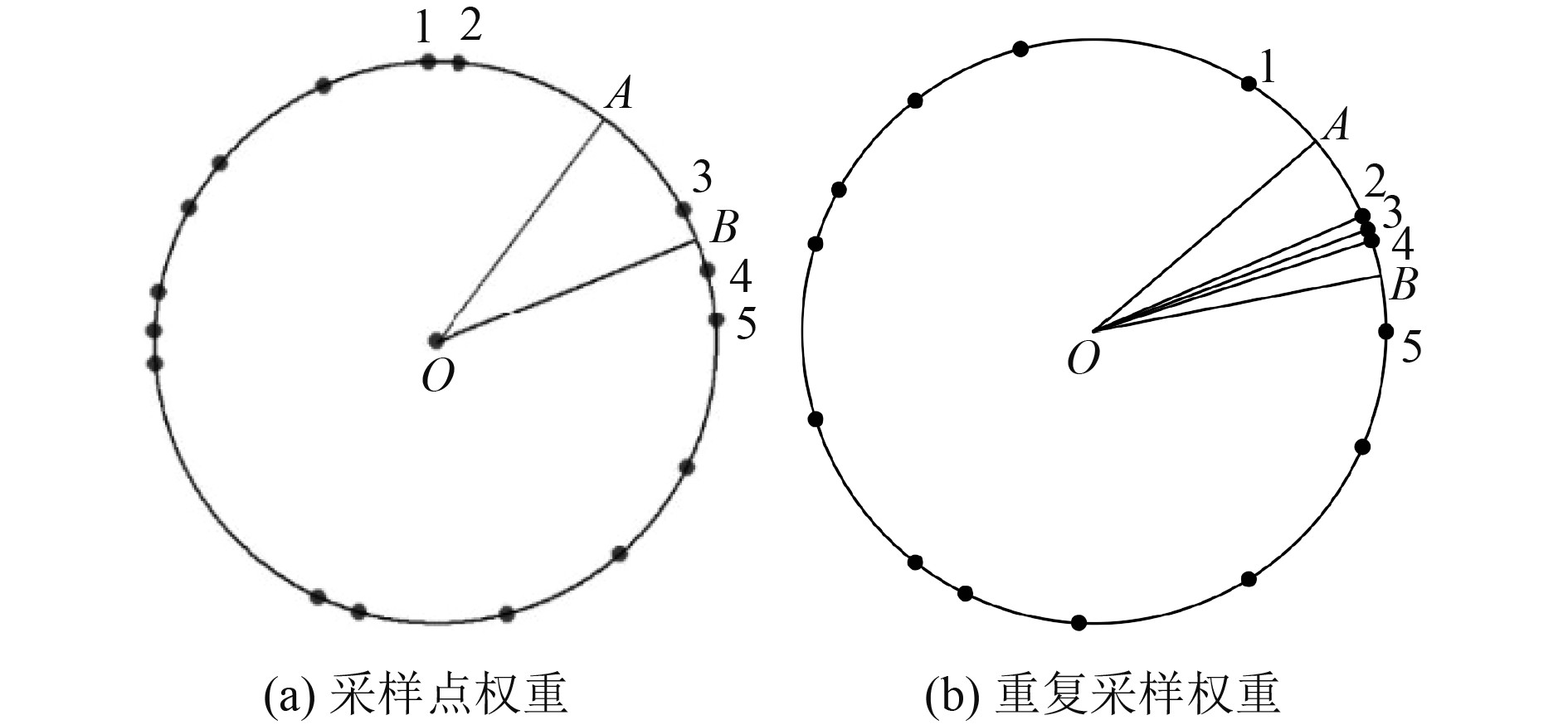
近年来，圆曲线的最小二乘拟合理论不断完善与丰富，从18世纪末19世纪初提出的最小二乘法乘（Least Square，LS）^[8-10]，到加权最小二乘法（Weighted Least Square，WLS），能够同时考虑观测向量和系数矩阵的误差的总体最小二乘法^[11-12]，由总体最小二乘法扩展的加权总体最小二乘法（Weighted Total Least Squares，WTLS）^[13-16]等，这些加权方法主要是应用于平面、曲面拟合及GPS高程拟合等。对于圆拟合，采样点的分布情况对拟合精度也有较大影响，在条件允许的情况下，应尽量在整个圆周上均匀采集离散点，才能得到最佳拟合效果^[17]，如图1（a）所示。

对于在役潜艇，在实际圆度评定过程中，经常会出现结构内部较为复杂的情形，特别是各种结构的遮挡，导致测量得到测点是非均匀的，如图1（b）所示。同时，随着多设备融合测量技术发展^[18-19]，复杂环境下，圆周上不同部位可能采用多台或不同的仪器设备进行数据采集，有的方法采集点密一些，有的方法采集点疏一些，这样也会导致整体采样的不均匀性，如图1（c）和图1（d）所示。上述几种情况会对经典最小二乘圆拟合结果产生较大的影响；本文提出一种基于非均匀采样的加权总体最小二乘法，从理论上同时考虑观测向量和系数矩阵的扰动，用于处理非均匀采样带来的影响；这里的加权是依据测点的分布来确定权重，以此来提高非均匀采样情况下最小二乘圆的拟合精确。

1 加权总体最小二乘法的基本原理

线性方程中 $ {\boldsymbol{AX }}= {\boldsymbol{L}} $ ，最小二乘的原理是在残差平方和极小的情况下求出参数的最佳估计值。该方法的前提条件之一是假定系数矩阵 $ {\boldsymbol{A}} $ 是由没有误差的精确值构成的，而只对观测值 $ {\boldsymbol{L}} $ 矩阵进行改正，但实际上，观测向量 $ {\boldsymbol{L}} $ 、系数矩阵 $ {\boldsymbol{A}} $ 都有扰动。因此从理论上讲应该同时考虑 $ {\boldsymbol{L}} $ 和 $ {\boldsymbol{A}} $ 的扰动才严密，也就是说同时顾及观测向量 $ {\boldsymbol{L}} $ 和系数矩阵 $ {\boldsymbol{A}} $ 的误差^[15]，建立EIV模型：

$ ({\boldsymbol{A}} + {{\boldsymbol E}_A}){\boldsymbol{X}} = {\boldsymbol{L}} + {{\boldsymbol{e}}_L} ，$

(1)

且 $\left[ \begin{array}{c}{{\boldsymbol{e}}}_{L}\\ \text{vec}({{\boldsymbol E}}_{A})\end{array} \right]=\left\{\left[ \begin{array}{c}0\\ 0\end{array} \right]，{\sigma }_{0}^{2}\left[ \begin{array}{cc}{{\boldsymbol{Q}}}_{L}&{} \\{} & {{\boldsymbol{Q}}}_{A}\end{array} \right]\right\}$ 。其中 ${\boldsymbol{A}} \in {{\boldsymbol{R}}^{m \times n}}$ ， ${\boldsymbol{L}} \in {{\boldsymbol{R}}^m}$ ， ${\boldsymbol{X}} \in {{\boldsymbol{R}}^n}$ ， ${\text{rank}}\left( {\boldsymbol{A}} \right) = n < m$ 。 $ m $ 为条件方程个数； $ n $ 为待估参数个数； ${{\boldsymbol{e}}_L}$ 为观测阵的误差； ${{\boldsymbol{E}}_A}$ 为系数阵的误差；vec表示将矩阵按列拉直，依次从左到右； ${{\boldsymbol{e}}_A} = {\text{vec}}\left( {{{\boldsymbol{E}}_A}} \right)$ 。其中， ${{\boldsymbol{Q}}_L}$ 和 ${{\boldsymbol{Q}}_A}$ 分别为 ${{\boldsymbol{e}}_L}$ 和 ${{\boldsymbol{e}}_A}$ 的对称非负定协因素阵， $ \sigma _0^2 $ 是未知的单位权方差， ${{\boldsymbol{P}}_L} = {{\boldsymbol{Q}}_L}^{ - 1}$ ， ${{\boldsymbol{P}}_A} = {{\boldsymbol{Q}}_A}^{ - 1}$ ， ${{\boldsymbol{P}}_L}$ 和 ${{\boldsymbol{P}}_A}$ 分别为观测值 ${\boldsymbol{L}}$ 与 ${\boldsymbol{A}}$ 所对应的观测量之间的2个权阵^[15]。加权总体最小二乘的基本准则为:

$ {\boldsymbol{e}}_L^{\rm{T}}{{\boldsymbol{P}}_L}{{\boldsymbol{e}}_L} + {\boldsymbol{e}}_A^{\rm{T}}{{\boldsymbol{P}}_A}{{\boldsymbol{e}}_A} = \min ，$

(2)

依据式(4)的模型，以及上述定义的各参数，定义 ${{\boldsymbol{Q}}_A} = {{\boldsymbol{Q}}_0} \otimes {{\boldsymbol{Q}}_X}$ , ${{\boldsymbol{Q}}_0} = {{\boldsymbol{P}}_0}^{ - 1}$ , ${{\boldsymbol{Q}}_X} = {{\boldsymbol{P}}_X}^{ - 1}$ , ${{\boldsymbol{P}}_A} = {{\boldsymbol{P}}_0} \otimes {{\boldsymbol{P}}_X}$ ，称 ${{\boldsymbol{P}}_0}$ 为系数矩阵 ${\boldsymbol{A}}$ 的列向量权阵， ${{\boldsymbol{P}}_X}$ 为系数矩阵 ${\boldsymbol{A}}$ 的行向量权阵^[15]，“ $ \otimes $ ”为Kronecker积。建立目标函数:

$ \begin{split} {\boldsymbol{\varPhi}} \left({{\boldsymbol{e}}}_{L}\text{，}{{\boldsymbol{e}}}_{A}\text{，}{\boldsymbol{\lambda}} \text{，}{\boldsymbol{X}}\right)=& {{\boldsymbol{e}}}_{L}^{{\rm{T}}}{{\boldsymbol{P}}}_{L}{{\boldsymbol{e}}}_{L}+{{\boldsymbol{e}}}_{A}^{{\rm{T}}}\left({P}_{0}\otimes {{\boldsymbol{P}}}_{X}\right){{\boldsymbol{e}}}_{A}+\\ & 2{\lambda }^{{\rm{T}}}\left({\boldsymbol{L}}+{{\boldsymbol{e}}}_{L}-{\boldsymbol{AX}}-\left({{\boldsymbol{X}}}^{{\rm{T}}}\otimes {{\boldsymbol{I}}}_{n}\right)\cdot {{\boldsymbol{e}}}_{A}\right)。\end{split} $

(3)

其中，向量 $ {\boldsymbol{\lambda}} $ 是 $ m \times 1 $ 阶拉格朗日乘数，对 $ {\boldsymbol{\varPhi}} $ 求拉格朗日极值，求各参数的一阶偏导数并令其等于0，然后按照最小二乘各平差方法的推求原理^[15]，进行迭代求解。

2 非均匀采样加权总体最小二乘法 2.1 非均匀采样点权重的确定

当潜艇耐压壳体肋骨剖面圆的圆周上采样 $m$ 个测点沿圆周完全均匀分布时，其权重应相同，w₁=w₂=…=w_m=w₀。当测点沿圆周不均匀分布时，通过赋值各点的权重，使得拟合圆心和半径尽可能接近真值，或者接近测点均匀分布时的拟合结果。当同一位置某测点 ${S_i}({x_i},{y_i})$ （1≤i≤m）有 $k$ 次重复测量数据时，每个重复采样数据的权重相同。

步骤1　中采用相同权重（可取所有测点权重均为1）进行最小二乘圆拟合，得到初步拟合结果（拟合圆圆心位置和半径），然后计算每个采样点对应的圆心角。如图2（a）所示，O为等权拟合圆圆心，A点为等权拟合圆上采样点2和3之间的中点，B点为等权拟合圆上采样点3和4之间的中点，则∠AOB即为采样点3所对应的圆心角 ${\alpha _3}$ ，其他采样点所对应的圆心角计算方法类似。

步骤2　中计算采样点权重，采用新的权重进行加权最小二乘圆拟合。权重计算公式为：

$ {w_i} = {\alpha _i}/\sum\limits_{i = 1}^m {{\alpha _i}}。$

(4)

当同一位置采集多次，或者多个采样点非常靠近时（圆弧距离小于100 mm——参考对圆柱形耐压分段，当有测点无法测量时，如有可能，可将测点移到离肋骨腹板100 mm之内进行测量^[20]），如图2（b）所示，取其中更靠近弧线AB的中点的采样点参与角度计算，得到相应权重，然后再将权重按重复次数均分。只有当重复采样是个数达到3个时，此判定条件才会对结果有一定的影响，但影响有限。

2.2 加权总体最小二乘法在非均匀采样圆拟合中的应用分析

潜艇耐压壳体的肋骨剖面一般为圆曲线形式，可设圆曲线的方程为：

$ {({x_i} - {x_0})^2} + {({y_i} - {y_0})^2} = {R^2} ，$

(5)

其中， $({x_0},{y_0})$ 为圆心坐标， $R$ 为半径。将式（5）展开得到：

$ {x_i}^2 + {y_i}^2 = 2{x_i}{x_0} + 2{y_i}{y_0} + {R^2} - {x_0}^2 - {y_0}^2。$

(6)

视 $ {x_i}^2 + {y_i}^2 $ 、 $ 2{x_i} $ 、 $ 2{y_i} $ 为新的观测值， $ {x_0} $ 、 $ {y_0} $ 、 $ {R^2} - {x_0}^2 - {y_0}^2 $ 为待估参数^[21]。运用加权总体最小二乘的思想，将式（6）写成矩阵形式为:

$ \left[ {\begin{array}{*{20}{c}} {{x_1}^2 + {y_1}^2} \\ {{x_2}^2 + {y_2}^2} \\ \cdot \\ \cdot \\ {{x_m}^2 + {y_m}^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {2{x_1}} & {2{y_1}} & 1 \\ {2{x_2}} & {2{y_2}}& 1 \\ \cdot& \cdot & \cdot\\ \cdot & \cdot& \cdot\\ {2{x_m}} & {2{y_m}} & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}} \\ {{y_0}} \\ {{R^2} - {x_0}^2 - {y_0}^2} \end{array}} \right] 。$

(7)

其中， ${\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{x_1}^2 + {y_1}^2} \\ {{x_2}^2 + {y_2}^2} \\ \cdot \\ \cdot \\ {{x_m}^2 + {y_m}^2} \end{array}} \right]$ , ${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {2{x_1}} \\ {2{x_2}} \\ \cdot \\ \cdot \\ {2{x_m}} \end{array}}&{\begin{array}{*{20}{c}} {2{y_1}} \\ {2{y_2}} \\ \cdot \\ \cdot \\ {2{y_m}} \end{array}}&{\begin{array}{*{20}{c}} 1 \\ 1 \\ \cdot \\ \cdot \\ 1 \end{array}} \end{array}} \right]$ , ${\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{x_0}} \\ {{y_0}} \\ {{R^2} - {x_0}^2 - {y_0}^2} \end{array}} \right]$ 。

对于协因素阵的确定，认为x，y是等精度的独立观测量，且观测向量与系数阵行向量相关。令 $ {\sigma _x} = {\sigma _y} $ ， $ l = ({x_i}^2 + {y_i}^2) $ ，则根据协因素传播律有 ${{\boldsymbol{Q}}_L} = 2( {x_i}^2 + {y_i}^2 ){{\boldsymbol{Q}}_X}$ ，其中 ${{\boldsymbol{P}}_X} = {{\boldsymbol{Q}}_X}^{ - 1}$ ，根据系数矩阵 ${\boldsymbol{A}}$ 的形式可知：

$ {{\boldsymbol{Q}}}_{0}=\text{diag}\left(2\text{，}2\text{，}0\right) $

(8)

认为观测向量之间等权，则对于权阵 ${{\boldsymbol{P}}_X}$ 可由非均匀的权重确定：

$ {{\boldsymbol{P}}_X} = {\boldsymbol{W}} = {\rm{diag}}\left( {{w_1},{w_2}, \cdots ,{w_m}} \right) 。$

(9)

3 非均匀采样圆拟合数值实验

潜艇建造中耐压体肋骨剖面实际形状通常为近似椭圆形状，为能既符合工程实际，又有标准拟合结果可参照比较，数值实验时选取近似圆形的标准圆进行数值采样。因圆心位置对拟合结果没有影响，将圆心直接设置在坐标原点位置，圆的半径为5000 mm。模拟在役潜艇耐压壳体的实际圆度情况，在标准圆的坐标值上，添加各种函数，如5sin2θ、(θ−π)²/2、椭圆、5(θ−jπ/3)²（j=1，3，5）等（0≤θ≤2π），作为预设的形状，如图3所示。用基于全站仪的激光圆度测量分析系统^[7]对潜艇耐压壳体进行测量时，考虑测量过程中存在的测量误差（极端复杂情况下测量误差为1.5 mm），在采样数据上添加服从正态分布的随机数来模拟测量误差，然后分别对均匀采样、部分测点重复采样、局部加密采样、非均匀采样4种情形进行圆拟合数值实验。以拟合圆的圆心坐标偏差、半径偏差作为评定标准，圆心和半径偏差指非均匀采样圆拟合的值与真值偏差的绝对值。

3.1 均匀采样

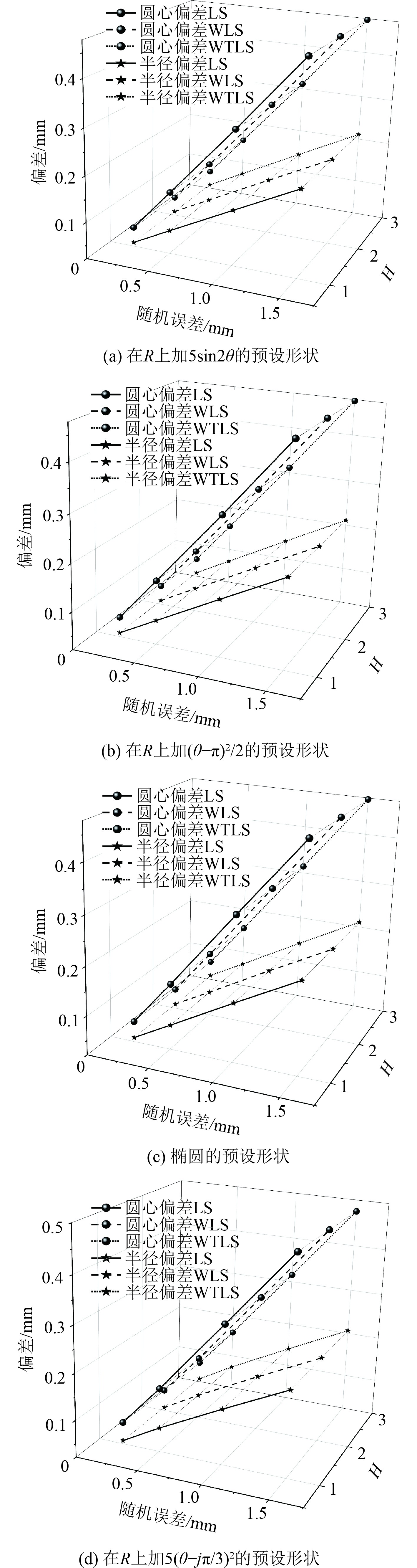
在同精度、均匀采集的前提下，文献[8]研究表明圆拟合过程中均匀采集15～20个离散点即可。因此，此处以均匀等分角在圆上采样32个点坐标，分别采用最小二乘圆拟合方法、加权最小二乘法及非均匀采样加权总体最小二乘圆拟合法进行圆拟合，比较3种方法在循环计算10000次求平均值时，各项偏差的大小，计算结果如图4所示。可知，均匀采样情况下，3种方法的拟合效果基本一致，不同的预设形状对均匀采样影响较小；整体的圆心偏差值大于半径偏差值，且随着加入的测量误差增大，各项偏差值也增大，符合一般的误差规律。

3.2 部分测点重复采样

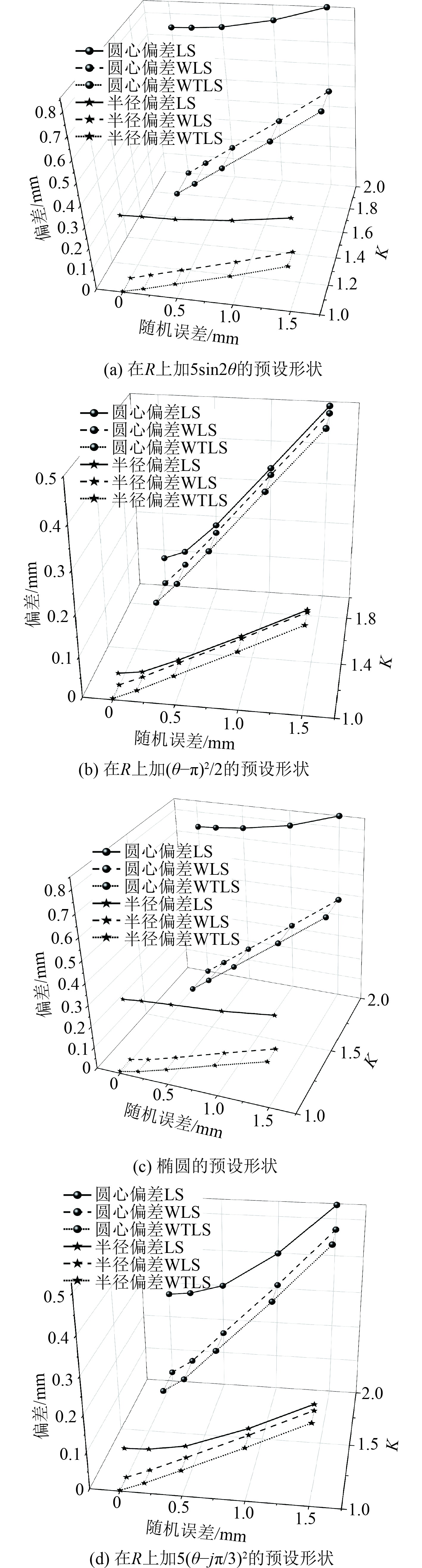
在部分相同位置点重复采样，会导致测点分布的不均匀性，这是实际工程测量中通过相互校验，提高测量可靠性时经常会出现的一种情况。为了验证3种算法对这种情况圆拟合的影响，随机选取1/4区域的测点进行重复采样，循环计算10000次后求平均值，计算结果如图5所示。可知，对于4种预设形状，当存在部分测点重复采样时，整体的圆心偏差值大于半径偏差值；随着加入的测量误差增大，整体的各项偏差值也增大，对于不同的预设形状圆心偏差趋势不同，半径偏差的变化趋势基本一致；对于圆心偏差和半径偏差，WTLS与WLS的拟合结果基本一致，WTLS的拟合结果比LS的拟合结果更好，偏差值更小。

3.3 局部加密采样

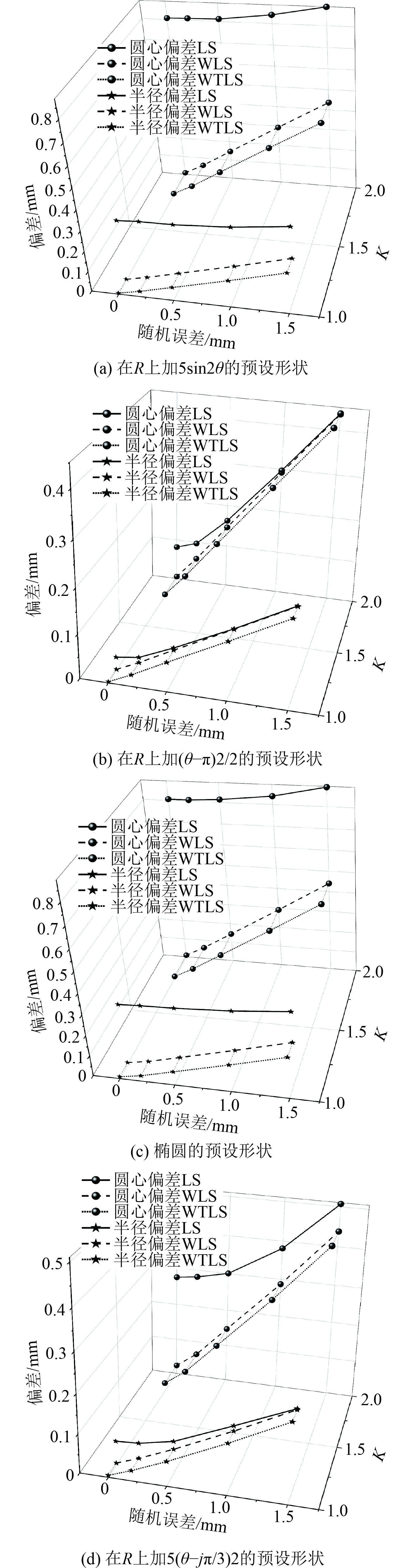
因测量方法的不同和融合测量技术的发展，局部加密采样也是工程实际中经常会遇到的情况之一，也会导致采样不均匀，为验证算法对局部加密采样拟合结果的影响，随机选取1/4区域的测点进行加密采样，然后进行圆拟合的10000次循环计算并求平均值，计算结果如图6所示。可知，对于加密采样，这4种预设形状，WTLS与WLS的拟合结果基本一致，WTLS的拟合结果比LS的拟合结果更好，偏差值都更小；随着加入的测量误差的增大，各项偏差值也增大，且整体的圆心偏差值大于半径偏差值，对于不同预设形状圆心偏差的趋势不同，半径偏差的变化趋势基本一致。

3.4 非均匀采样

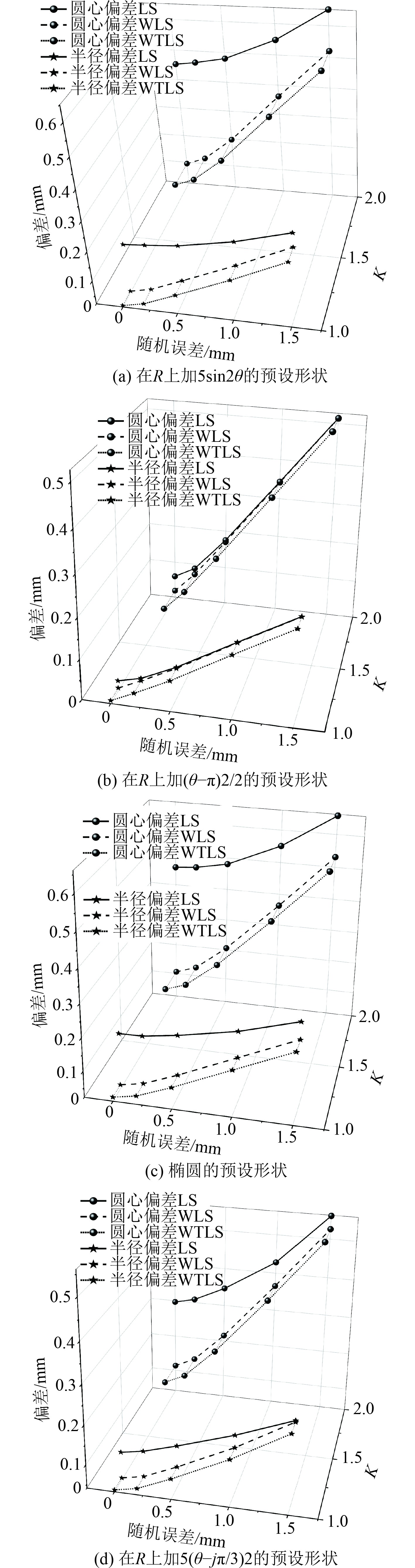
因等分测点被结构遮挡，或局部空间狭窄个别测点无法测量等现场条件限制，非均匀采样是工程实际中最常遇到的情况。非均匀随机采样，即先根据采样数量均匀等分，得到采样点的圆心角θ，然后在圆心角θ上叠加均值 $\mu {\text{ = }}0$ ，标准差 $\sigma {\text{ = }}2{\text{π}} /m$ 正态分布量，得到非均匀随机的点坐标。循环计算10000次后求平均值，计算结果如图7所示。可知，对于这4种预设形状，随着加入的测量误差增大，整体的各项偏差值都增大，对于不同的预设形状圆心偏差的趋势不同，半径偏差的变化趋势基本一致，整体的圆心偏差值大于半径偏差值；对于非均匀采样的情况，各项的偏差值，WTLS与WLS的拟合结果基本一致；由图7(b)可知，该预设形状下，随着误差的增大3种方法的结果基本一致，考虑此预设形状，权重对于随机非均匀采样影响较小；由图7(a)图7(c)图7(d)可知，WTLS的拟合结果比LS的拟合结果更好，偏差值都更小。

3.5 小　结

对于4种预设形状下的各种不均匀情况圆拟合计算结果，由图4～图7可知，整体的圆心偏差值大于半径偏差值，且随着加入的测量误差增大，整体的各项偏差值都增大；对于均匀采样，3种拟合方法的计算结果一致；对于部分测点重复采样、局部加密采样和非均匀采样，WTLS的拟合结果都比LS的好；WTLS与WLS的拟合结果基本一致，但在理论上WTLS比WLS更完备。

4 结　语

本文提出一种基于非均匀采样加权的加权总体最小二乘法用于潜艇耐压壳体测量数据的处理。研究表明，本文所提的非均匀采样加权总体最小二乘法，对4种预设形状下各种非均匀情况的圆拟合问题，可得到比经典最小二圆拟合法更好的精度，且与加权二乘法相比理论更加完备。该方法可用于在役潜艇耐压壳体肋骨剖面圆度评估，尤其是在役潜艇修理时复杂环境下的非均匀采样数据圆拟合。