2. 上海外高桥造船有限公司,上海 200137;
3. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212100
2. Shanghai Waigaoqiao Shipbuilding Co., Ltd., Shanghai 200137, China;
3. School of Civil Engineering and Architecture, Jiangsu University of Science and Technology, Zhenjiang 212100, China
LNG船运输过程中会产生船体的横摇,从而引起货物重心加速度并产生压力。对于液货舱内部压力的研究,钟晓晶等[1]考虑到船舶运动会产生3个方向上货物加速度,对A型独立液货舱压力计算时采用Visual Basic软件编程。通过输入液货舱的位置、形状等基本信息,计算出液货舱内各点的压力。黎智昌等[2]根据三维载荷的情况,对C型独立液货舱进行实例分析,用有限元软件对液罐内部压力计算分析,得出最大压力。
吴嘉蒙等[3]对比分析二维加速度椭圆法和三维加速度椭球法,针对220 000 m3薄膜型LNG船,提出GM值影响液货舱内部压力的假设并进行讨论。朱达新[4]建立三维立体模型对A型液货舱内部压力进行分析,从最大倾斜角中得出合成加速度,计算出最大液柱高度,从而推导出液货舱内部压力解析公式。娄本强等[5]采用三维加速度椭球法,使用PTC. MathCAD中编程实现对C型液货舱内部指定参考点的压力极值迭代计算。
本文基于国际海事组织(IMO)的《国际散装运输液化气体船舶构造与设备规则》[6]中对独立液货舱内部压力计算方法的更新,编制基于三维加速度椭球法解析的软件工具,计算薄膜型液货舱内部压力,与二维速度椭圆法的结果进行比较,并与DNV船级社现有计算工具的计算结果进行对比,发现本工具的精度高,并可以实现“多参考点”——“多目标点”罐内压力的迭代计算。将该工具应用于C型液货舱内部压力的计算中,研究液货舱内部压力沿着船宽方向和船长方向的分布,找到最大压力的大致位置,并讨论横稳心高GM值对液货舱内部压力的影响。
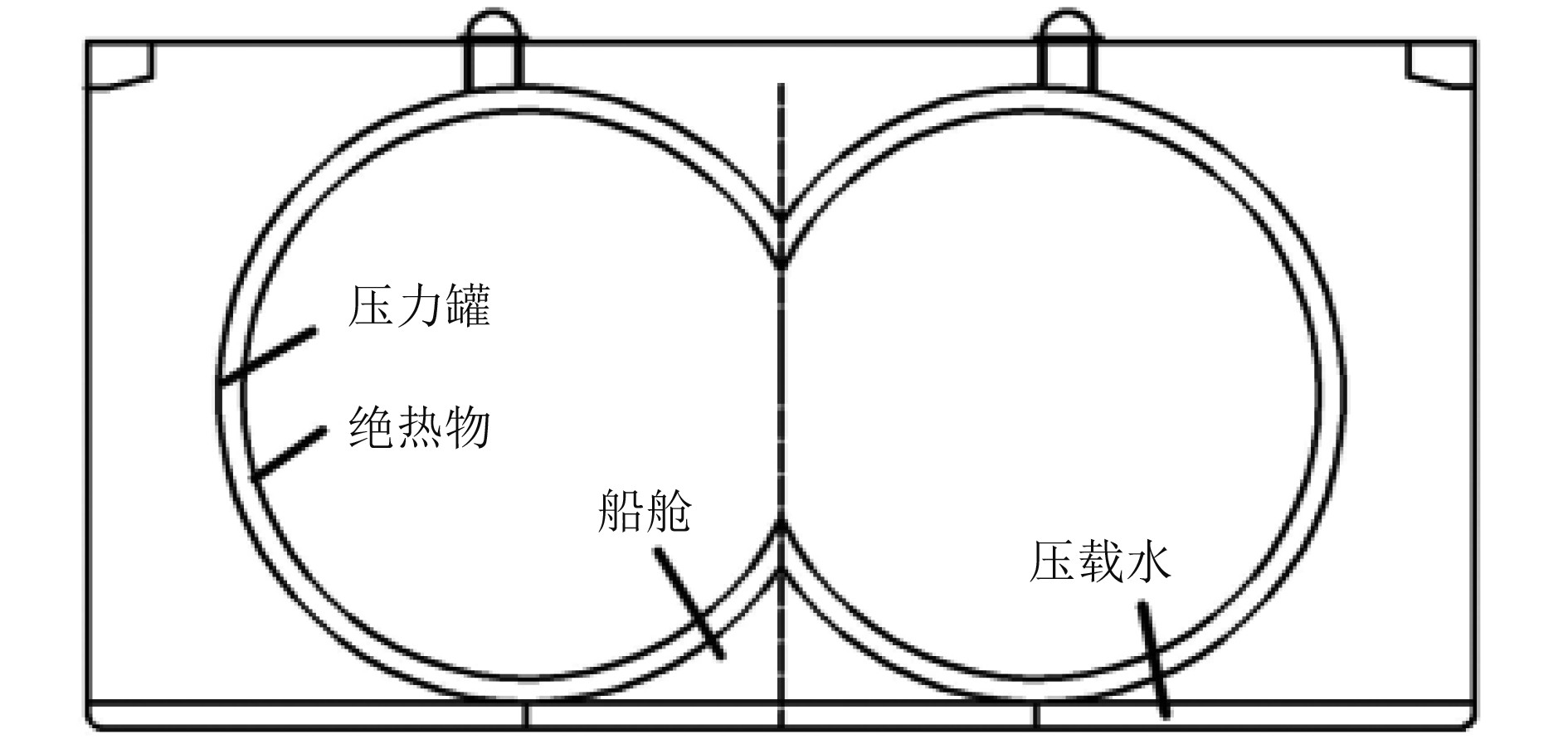
|
图 1 C型舱横剖面图 Fig. 1 Cross section view of type C tank |
根据IGC的规定,液货舱内部压力Peq由蒸汽压力 P0和内部液体压力 Pgd 组成,即
| $ {P_{eq}} = {P_0} + {\left( {{P_{{{gd}}}}} \right)_{\max }}。$ | (1) |
其中,
| $ {p_{gd}} = {\alpha _\beta }{Z_\beta }\left( {\frac{\rho }{{1.02 \times {{10}^5}}}} \right) 。$ | (2) |
式中:
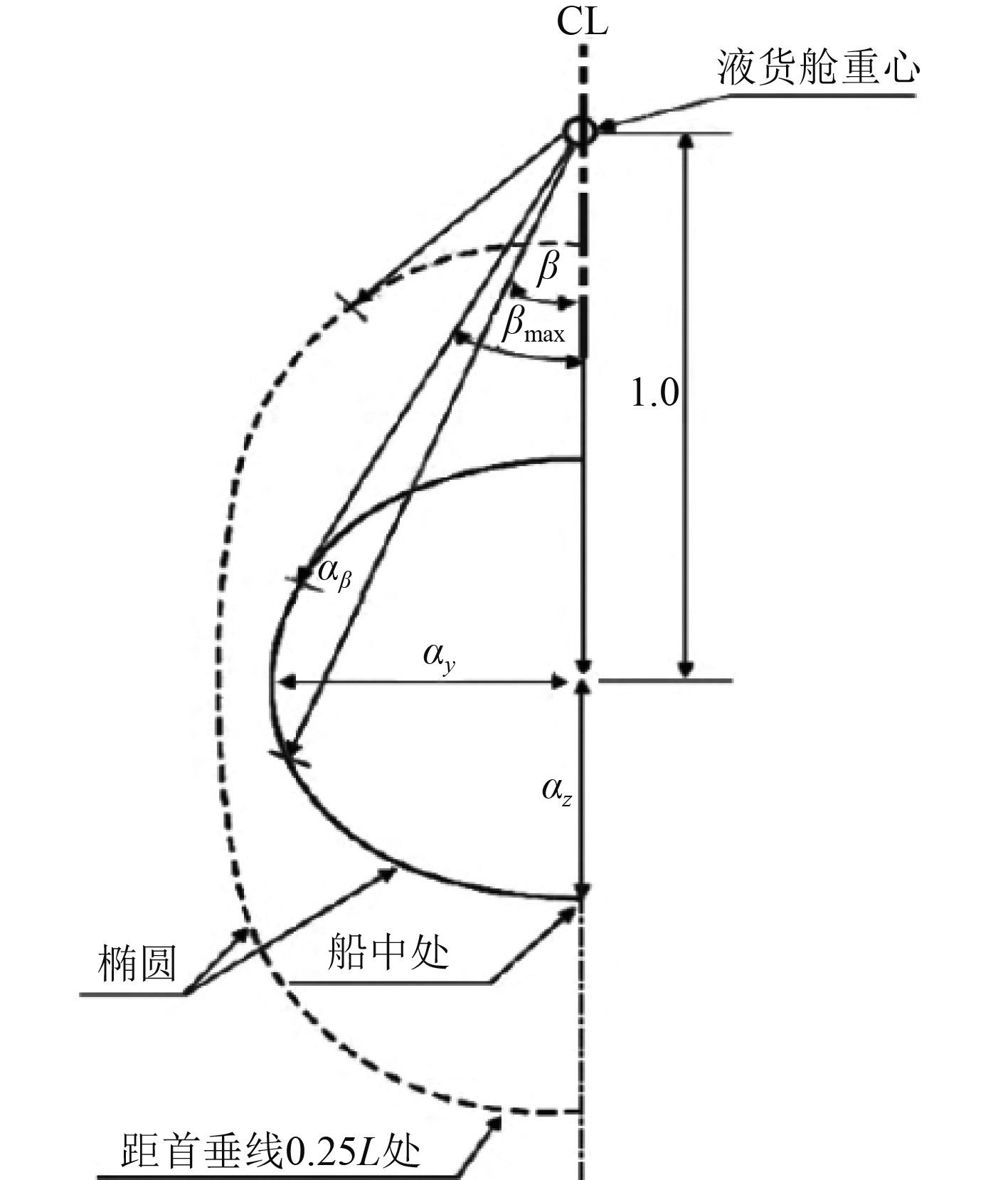
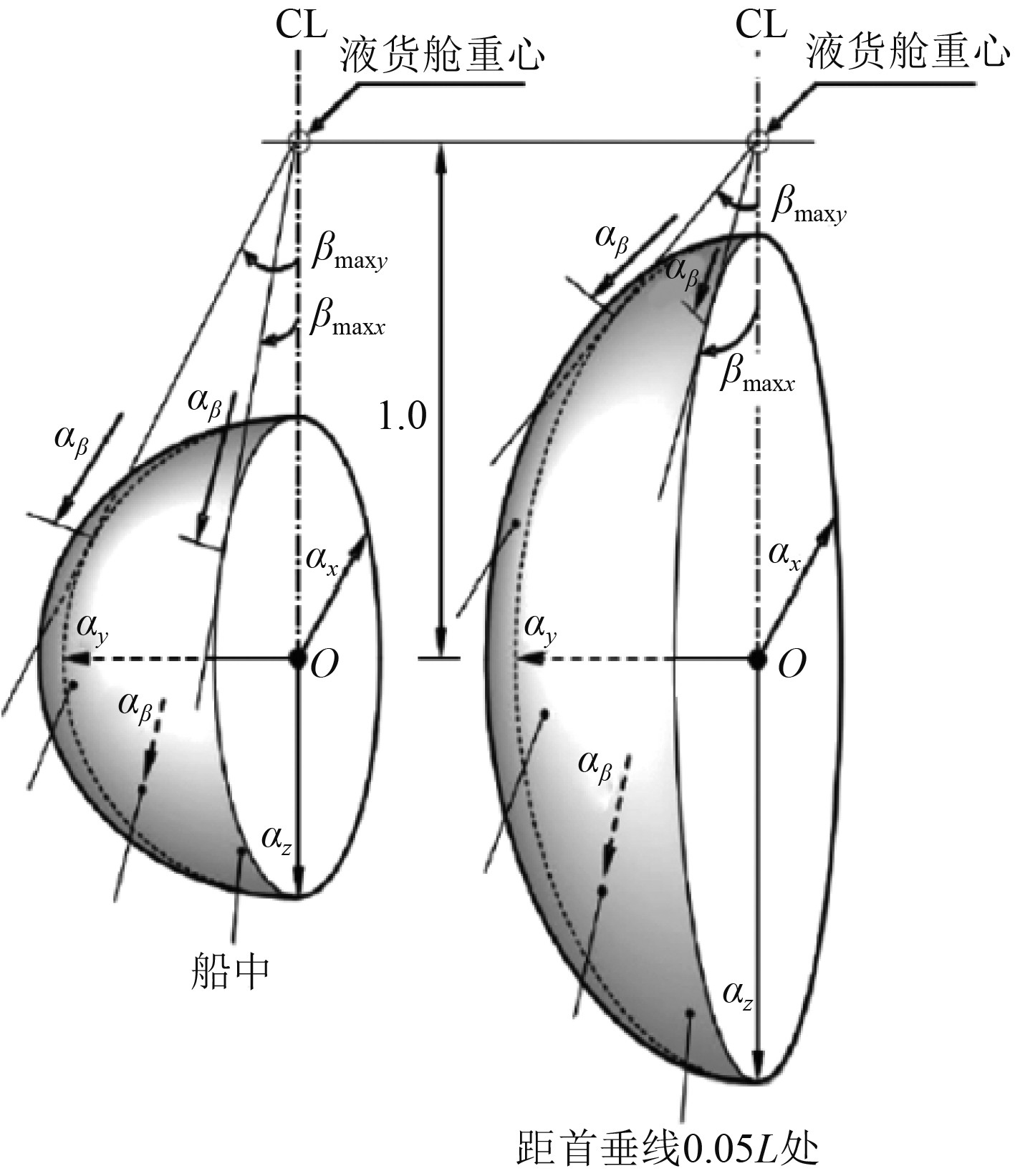
其中,可以使用二维加速度椭圆法[7](见图2)和三维加速度椭球法[8] (见图3)计算加速度。二维加速度椭圆法比较传统,合成“纵向+横向”2个方向的加速度进行,而三维加速度椭球法是基于《规则》的更新,合成“纵向+横向+垂向”3个方向的加速度。
|
图 2 加速度椭圆 Fig. 2 Acceleration ellipse |
|
图 3 加速度椭球 Fig. 3 Ellipsoid of acceleration |
在更新的 IGC规则中,使用三维加速度椭球代替二维加速度椭圆。三维加速度椭球法公式见参考文献[5]。
采用解析法,
| $ {\alpha _\beta } = \left( {0,0,1} \right) + \left( {{\alpha _{{x}}}\cos \varphi ,{\alpha _y}\sin \varphi \cos \theta ,{\alpha _z}\sin \varphi \sin \theta } \right)。$ | (3) |
利用向量数量积法得到
| $ \begin{split} & {\alpha _\beta }{{\rm Z}_\beta } = \left( {{z_0} - {z_1}} \right) +\\ & \sqrt {{{\left[ {{\alpha _x}\left( {{x_1} - {x_0}} \right)} \right]}^2} + {{\left[ {{\alpha _y}\left( {{y_1} - {y_0}} \right)} \right]}^2} + {{\left[ {{a_z}\left( {{z_1} - {z_0}} \right)} \right]}^2}} ,\end{split} $ | (4) |
得到三维加速度椭球法公式:
| $ \begin{split} & {P_{gd}} = \rho g\Biggr[ \left( {{z_0} - {z_1}} \right) +\\ & \sqrt {{{\left[ {{\alpha _x}\left( {{x_1} - {x_0}} \right)} \right]}^2} + {{\left[ {{\alpha _y}\left( {{y_1} - {y_0}} \right)} \right]}^2} + {{\left[ {{a_z}\left( {{z_1} - {z_0}} \right)} \right]}^2}} \Biggr] 。\end{split} $ | (5) |
二维加速度椭圆法的公式可参考文献[9]:
| $ {P_{gd}} = \rho {\text{g}}\left[ { - \left( {{z_1} - {z_0}} \right) + \sqrt {{{\left[ {{\alpha _y}\left( {{y_1} - {y_0}} \right)} \right]}^2} + {{\left[ {{a_z}\left( {{z_1} - {z_0}} \right)} \right]}^2}} } \right] $ | (6) |
式中,液罐重心处3个方向产生的最大无因次加速度分量
纵向加速度:
| $ {\alpha _{{x}}} = \pm {\alpha _0}\sqrt {0.06 + {A^2} - 0.25A} 。$ | (7) |
横向加速度:
| $ {\alpha _y} = \pm {\alpha _0}\sqrt {0.6 + 2.5{{\left( {\frac{X}{{{L_0}}} + 0.05} \right)}^2} + K{{\left( {1 + 0.6K\frac{z}{B}} \right)}^2}}。$ | (8) |
垂向加速度:
| $ \begin{split} & {\alpha _z} =\\ & \pm {\alpha _0}\sqrt {1 + {{\left( {5.3 - \frac{{45}}{{{L_0}}}} \right)}^2}{{\left( {\frac{x}{{{L_0}}} + 0.05} \right)}^2}{{\left( {\frac{{0.6}}{{{C_b}}}} \right)}^{1.5}} + {{\left( {\frac{{0.6y{K^{1.5}}}}{B}} \right)}^2}}。\end{split} $ | (9) |
根据解析推导,用三维加速度椭球法得到的液货舱内部压力极值为:
| $ \begin{split} & {P_{eq}} = {P_0} + \max \Biggr\{ \rho g\Biggr[ \left( {{z_0} - {z_1}} \right) + \\ & \left. \sqrt {{\left[ {{\alpha _x}\left( {{x_1} - {x_0}} \right)} \right]}^2} + {{\left[ {{\alpha _y}\left( {{y_1} - {y_0}} \right)} \right]}^2} + {{\left[ {{a_z}\left( {{z_1} - {z_0}} \right)} \right]}^2} \right] \Biggr\}。\end{split} $ | (10) |
根据IGC规则的更新,对液货舱内部压力的方法进行介绍。由于采用该方法时迭代次数冗长,计算量偏大,耗时较多,为了在实际应用中缩短计算时间,提高三维加速度椭球法的计算效率,基于三维加速度椭球法解析式,利用 Python计算机语言,编写了三维加速度计算程序。选取某典型薄膜型液舱为研究对象(见图4),分别采用本文研发工具、二维加速度椭圆法对指定位置(液舱8个折角点)[3]的内部压力进行计算,并利用已有的DNV计算工具计算薄膜型液舱内部压力,进行精度分析。
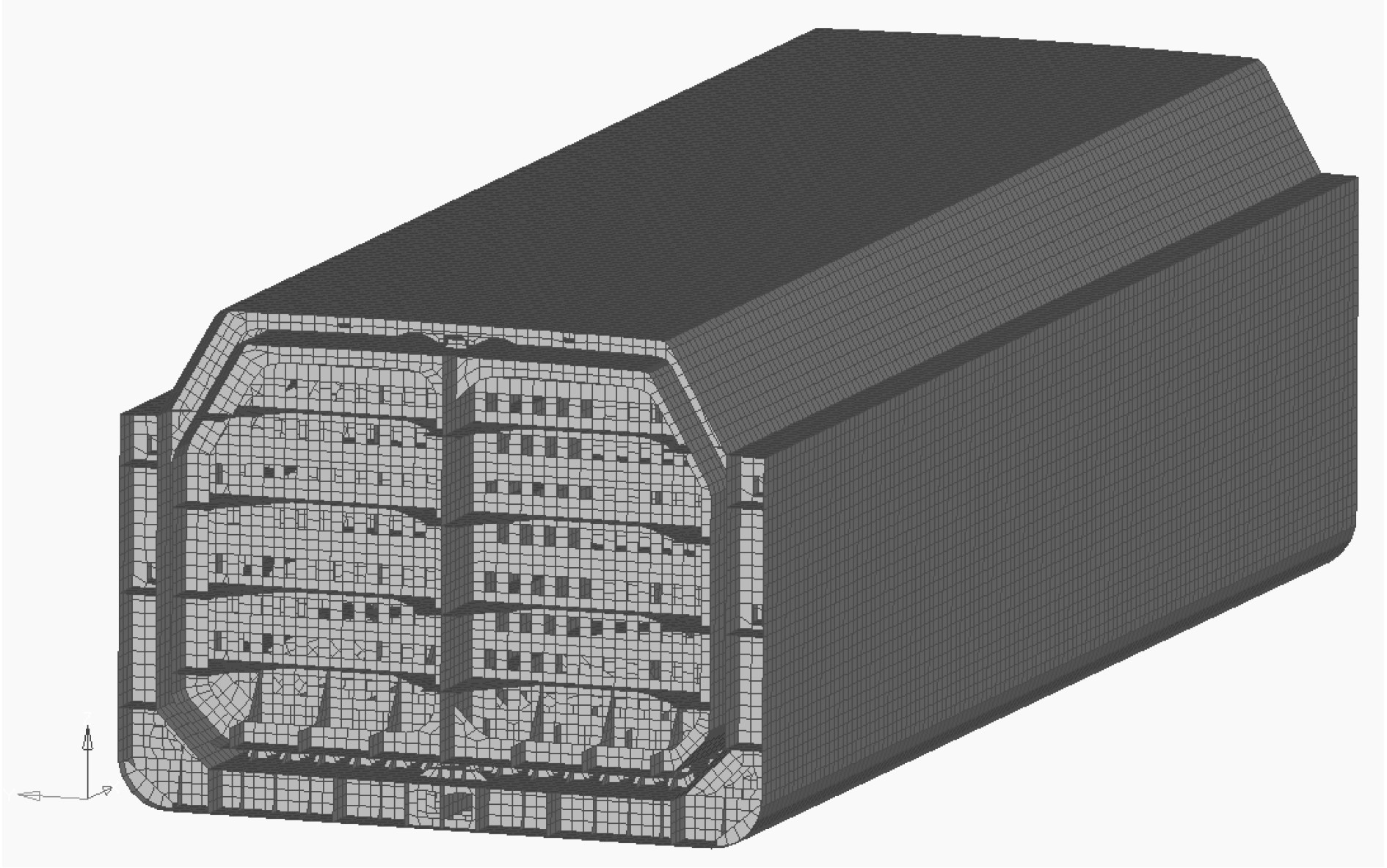
|
图 4 某薄膜型液舱三维外形图 Fig. 4 Three-dimensional shape diagram of membrane tank |
如表1所示,通过精度分析发现,本程序基于三维加速度椭球法的计算结果与DNV计算的结果基本一致,误差较小。而二维加速度椭圆法的计算压力结果与本程序的计算和DNV软件的计算都偏差较大。可知,本文开发的程序可很好模拟三维加速度椭球法计算,具有准确、高效及界面友好的特点,更加便于实际应用。
|
|
表 1 DNV船级社计算软件与二维加速度椭圆法、三维加速度椭球法压力计算比较 Tab.1 Comparison of pressure calculation software of DNV classification society with two dimensional acceleration ellipse method and three dimensional acceleration ellipsoid method |
以某22 000 m3 C型LNG船为研究对象,选取第二罐体,利用Patran建立液货舱模型(见图5),并细化模型网格,确保计算的精度,导出约30 000个参考点。初始设计蒸汽压力为 0.36 MPa,液货物密度设定为 0.61 t/m3 。为实现快速将计算参考点坐标和目标点坐标(见图6(a))同时输入软件中,代入三维加速度椭球解析式计算液货舱最大内部压力。利用 Python编写程序,自动进行解析式计算,并从LNG罐体的模型中选取6个典型肋位(液罐封头处、筒体处)[10]横剖面的参考点(见图6(b))进行分析。

|
图 5 独立C型液货舱 Fig. 5 Independent C type cargo tank |
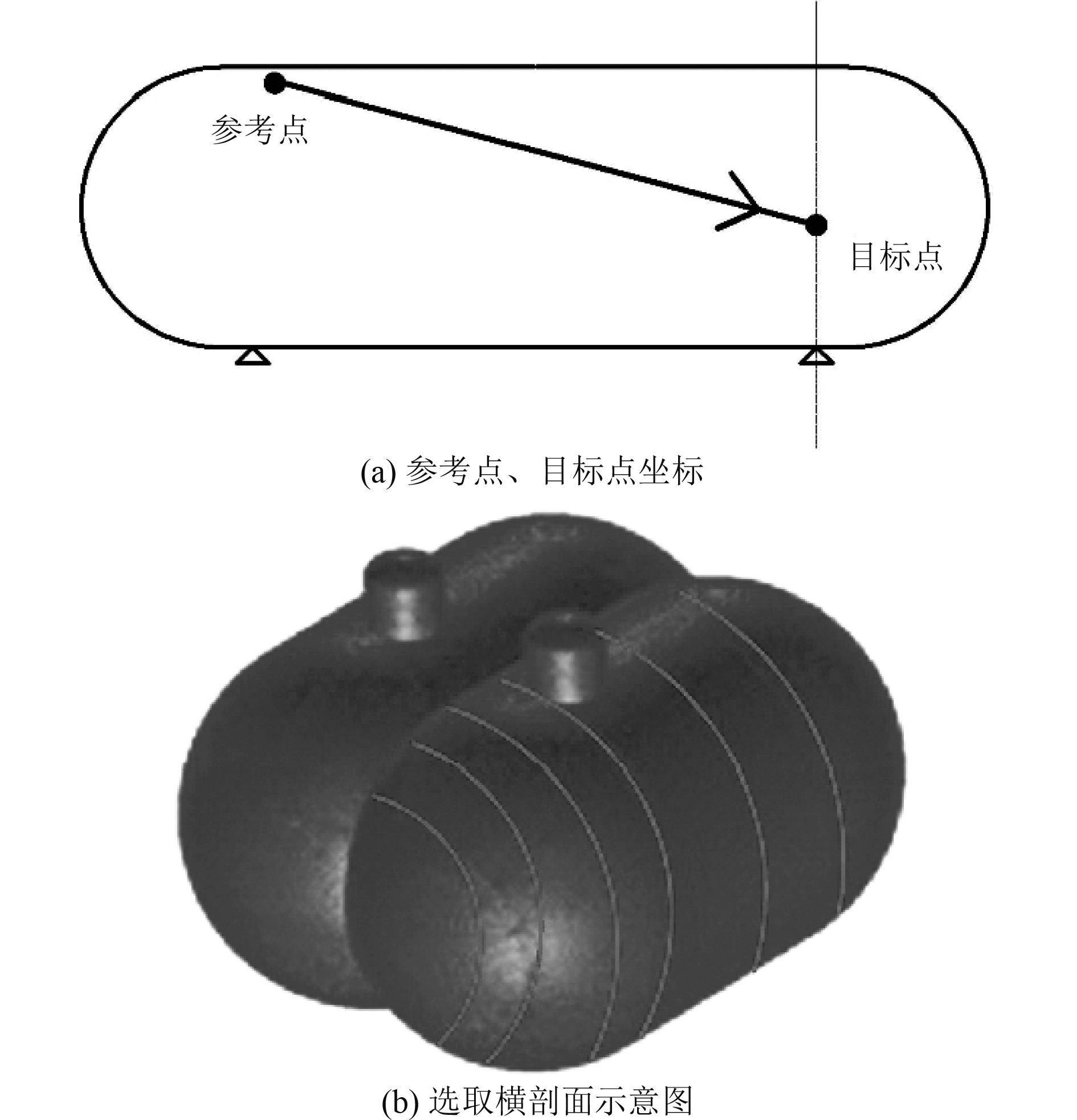
|
图 6 液货舱内部压力计算 Fig. 6 Calculation of internal pressure in cargo tank |
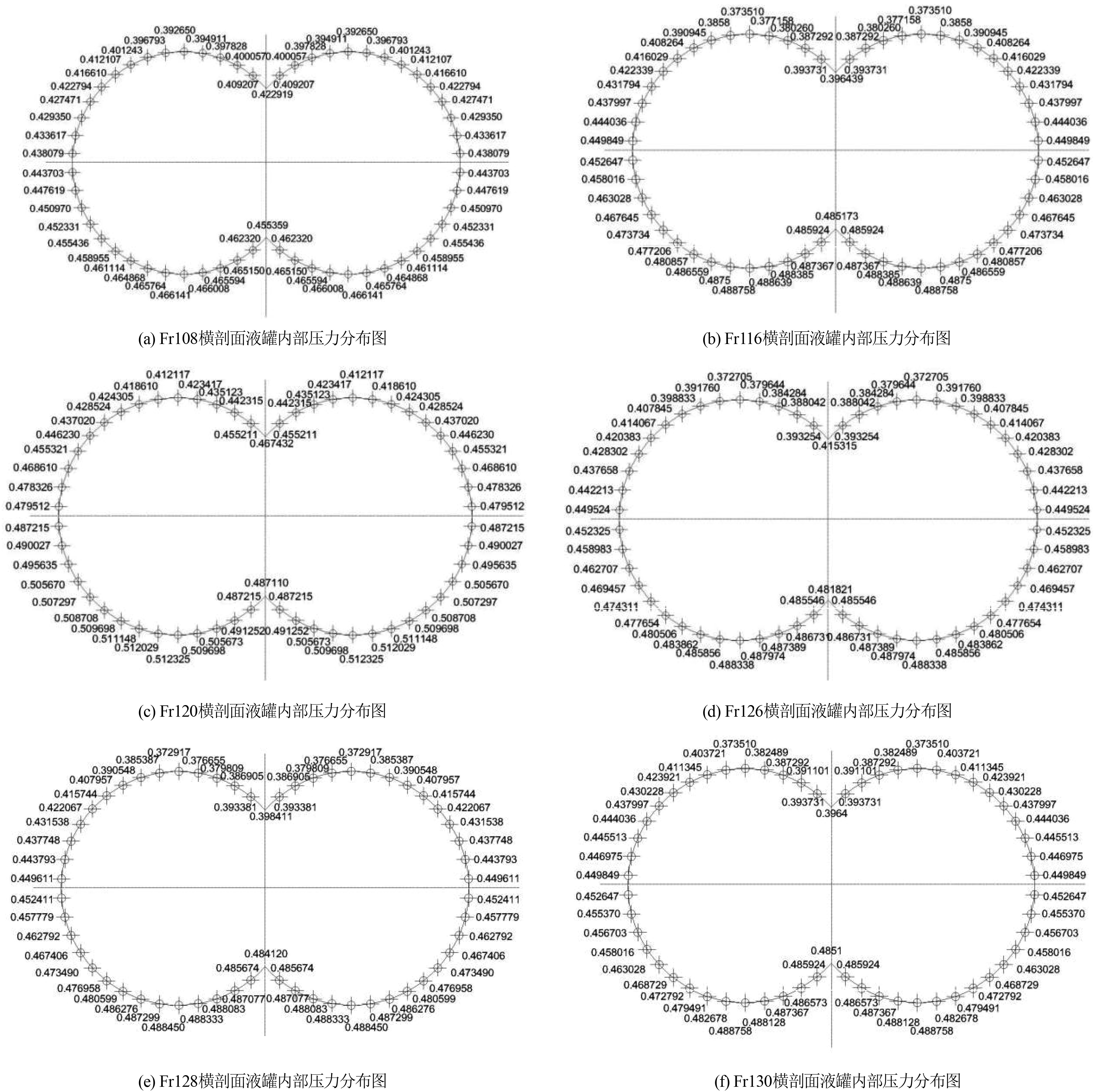
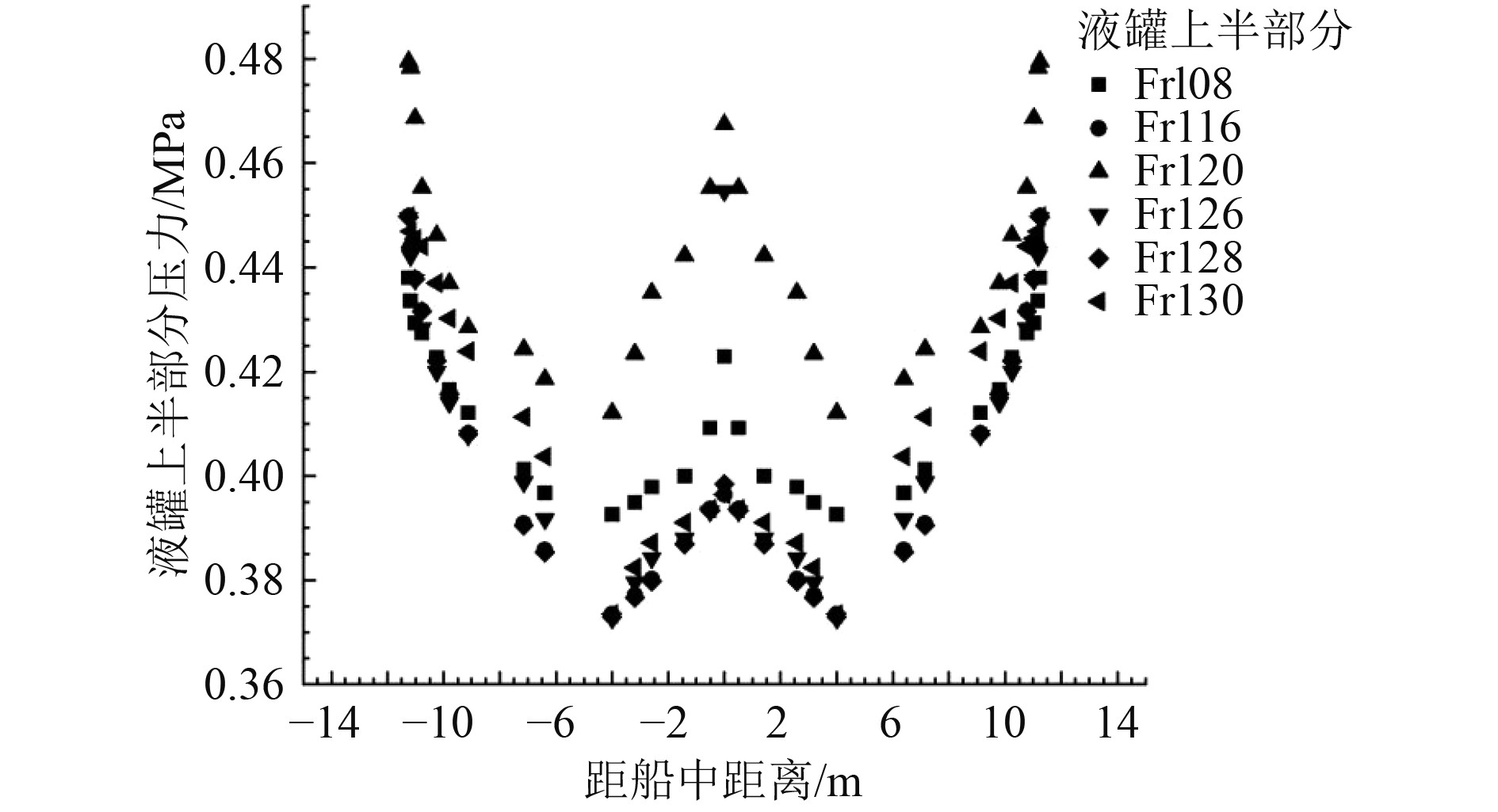
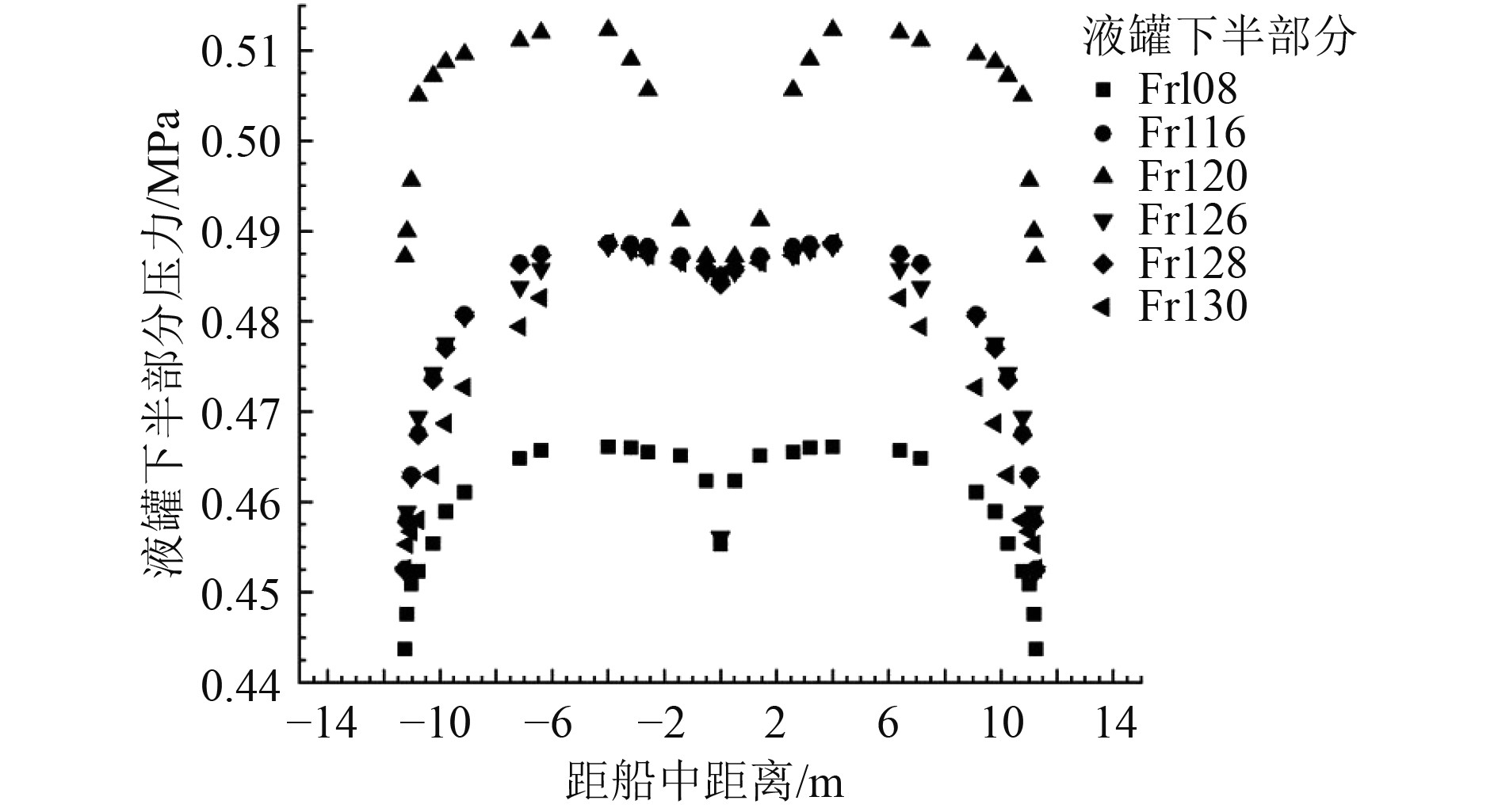
根据三维加速度计算程序,代入坐标点运算,总共耗时约60 s,计算得出液罐内部所有坐标点的压力值结果。选取的横剖面压力分布结果如图7所示,图8为液罐上半部分压力分布图,图9为液罐下半部分压力分布图,图10为液罐沿船长方向典型横剖面的同一纵剖面选取部分点的压力分布图。
|
图 7 典型肋位横剖面液罐内部压力分布图 Fig. 7 Diagram of pressure distribution inside tank in typical rib cross section |
|
图 8 液罐上半部分压力分布图 Fig. 8 Pressure in the upper half of the tank |
|
图 9 液罐下半部分压力分布图 Fig. 9 Pressure in the lower half of the tank |

|
图 10 沿船长方向典型横剖面的同一纵剖面选取部分点的压力分布图 Fig. 10 The pressure distribution diagram of some points along the same longitudinal section of a typical transverse section in the direction of the captain was selected |
选取第二罐体的6个典型肋位横剖面的最大压力值分布图,可分析得出:
1)液罐内部压力沿横剖面的分布规律
液罐左右两罐体的压力呈对称分布,液罐上半部分的压力小于下半部分的压力;越靠近罐子底部压力越大,其中在液罐底部区域(液罐底部和支撑结构接触区域)达到内部压力最大值;
2)液罐内部压力沿船长方向分布规律
液罐两封头处压力最大,罐中次之,封头到罐中之间压力较小。
本文研究的液罐内部压力最大值在封头底部区域(液罐底部和支撑结构接触区域),液罐内部压力最大值达到0.512 MPa。
4 横稳心高GM值对 C型液货舱内部压力影响当船长超过50 m,并以接近营运速度航行的船舶对应于北大西洋10−8概率水平船舶运动而产生的加速度分量有纵向加速度、横向加速度和垂向加速度,而横稳心高的值往往对无因次横向加速度ay产生一定影响[3]。为开展横稳心高GM值对C型液货舱内部压力的影响研究,针对本文典型液化气船,按IGC规范:
| $ k = \frac{{13GM}}{B}。$ | (11) |
式中:K为1,对于特殊的船型或装载工况,K
根据IGC规则,GM的计算法是从初始值

|
图 11 不同GM值时液货舱的内部压力 Fig. 11 Internal pressure of cargo tank at different GM values |
可知:随着GM值增加,液货舱内部压力也逐渐变大,其中在Fr 108(82.18,2.84,5.07),Fr108(82.18,4,4.91),Fr120(91.32,4,2.16),Fr120(91.32,3.39,2.19),Fr126(96.42,0.51,15.77),Fr126(96.42,1.80,16.32),Fr130(99.24,1.41,16.19)时,液货舱内部压力增幅较小;而在Fr116(88.68,10.24,5.73),Fr116(88.68,9.13,14.54),Fr 128(97.26,11.02,11.23),Fr128(97.26,11.25,9.62),Fr130(99.24,11.18,10.43)时,液货舱内部压力有一定的增幅。因此得出:横稳心高GM值对C型液货舱内部压力会产生一定的影响,其中沿高度方向在液货舱中间区域(最大液货舱宽度)液货舱内部压力随GM值增加的增幅相对较大。当横稳心高GM值从2 m增加到6 m时,液货舱内部压力增加约6 %;而液货舱上、下段内部压力则随GM值增加的增幅较小。
5 结 语本文根据三维加速度椭球法解析公式,代入坐标点计算,并分别与二维加速度椭圆法、三维加速度编程法、船级社软件的计算结果进行对比,讨论了横稳心高对液货舱内部压力的影响。
1)开展典型液化气船C型液货舱内部压力计算分析,分别采用DNV商用软件、三维加速度椭球法、二维加速度椭圆法、三维加速度编程法对某22 000 m3液化气船C型液货舱内部压力进行比较计算,表明三维加速度椭球法具有更好的计算精确性。同时本文基于三维加速度椭球法机理编写了三维加速度计算程序,经过对比计算,本程序具有准确、高效及界面友好的特点,更加便于实际应用。
2)液货舱内部压力分布的影响研究表明:液罐左右两罐体的压力呈对称分布,而液罐的上半部分的压力值小于下半部分的压力,沿纵向在液罐封头处压力最大;在液罐封头底部区域处(液罐底部和支撑结构接触区域),液货舱存在最大压力值,是船舶结构设计应重点关注的区域。
3)开展了横稳心高GM值对C型液货舱内部压力的影响研究,表明横稳心高GM值对液货舱内部压力分布有一定影响,在特殊装载工况下,沿高度方向在液货舱中间区域(最大液货舱宽度)液货舱内部压力会随着横稳心高GM的增加而变大。
| [1] |
钟小晶, 胡可一, 庄友榕. 液化气船A型独立液货舱内部压力计算方法和软件[J]. 造船技术, 1999(3): 27-29. |
| [2] |
黎志昌, 方江敏, 付小方. LNG运输船C型独立液货舱载荷及应力分析[J]. 船舶工程, 2011, 33(1): 1-4. DOI:10.3969/j.issn.1000-6982.2011.01.001 |
| [3] |
吴嘉蒙, 吕立伟, 蔡诗剑. 液化天然气船货舱内部压力研究[J]. 上海造船, 2011(1): 37-42. |
| [4] |
朱达新. 对液货舱内部压力计算的研究[J]. 广州航海学院学报, 2021, 29(2): 33-37. |
| [5] |
娄本强, 张洪军, 孙立, 等. 独立C型LNG运输船鞍座结构的数值模拟方法研究[J]. 江苏科技大学学报(自然科学版), 2021, 35(6): 1-8. |
| [6] |
IMO. International code for the construction and equipment of ships carrying liquefied gases in bulk (IGC Code)[S]. 2016.
|
| [7] |
Lloyd’s Register. Rules and regulations for the construction and classification of ships for the carriage of liquefied gases in bulk[S]. 2008.
|
| [8] |
Rules for Classification of Ships. Pt5. Ch. 5. Liquefied gas carriers[S]. Det Norske Veritas, 2007.
|
| [9] |
付喜华. 液化气船液货舱内部压力解析计算[J]. 船舶与海洋工程, 2018, 34(6): 7-11. DOI:10.14056/j.cnki.naoe.2018.06.002 |
| [10] |
王亮, 肖蕾, 陈熙. 液化气船独立液货舱内部压力计算方法研究与应用[J]. 船舶与海洋工程, 2020, 36(3): 17-20. DOI:10.14056/j.cnki.naoe.2020.03004 |
 2023, Vol. 45
2023, Vol. 45
