2. 广东海洋大学 电子与信息工程学院,广东湛江 524088;
3. 浙江大学 海洋学院,浙江 舟山 316021;
4. 宁波大学 海运学院,浙江 宁波 315211
2. School of Electronics and Information Engineering, Guangdong Ocean University, Zhanjiang 524088 China;
3. Ocean College Zhejiang University, Hangzhou 316021, China;
4. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China
快速性是包括浮性、稳性、耐波性以及操作性在内的船舶诸多性能中的重要性能之一[1-3]。快速性在船舶设计中占据着重要的地位。几乎每一艘船舶,在设计任务书中就给定明确的快速性指标。船舶的阻力性能是评估快速性的重要指标,对于船舶设计具有重要意义[4-5]。
船舶阻力同样与造船工程密切联系。船舶匀速前进和加速前进所遇到的阻力以及航行时的安全性,始终是造船工程中最重要的问题[6]。长期以来兴波阻力、附加质量、适航性等方面的研究都是为了解决这些问题的。随着造船技术的革新,各种复杂船型如水翼船、气垫船、多体船应运而生,这对水动力学及阻力分析提出更高的要求。在水中高速运行的水翼、鱼雷等产生的空泡流,快艇、赛艇、水上飞机的浮舟在水面上的滑行,船舶、闸门、管道等弹性体的振动,水面舰船、潜艇、鱼雷等所产生的水动力噪声等都是水动力学及阻力分析的重要研究课题。
阻力预报方法主要有理论分析、试验方法和数值模拟[7-8]。理论分析主要以船模试验或者实船试验得出的数据为基础,通过经验公式或图谱估算船舶阻力。船模试验是船舶阻力预报的最主要方法之一,其精度得到了工程界的广泛认可。但其缺点也显而易见:耗费高昂的时间和经济成本,每次能够测量的数据十分有限,且试验过程中存在很多需要修正的试验误差,如尺度效应、试验设备精度等。数值模拟是通过计算机手段求解流动方程,模拟船体周围流场,并得出阻力值和流场细节。此方法能够进行实尺度模拟,对于船舶阻力的研究起着重要作用。然而,数值模拟同样存在一定的局限性,如计算精度、网格划分、耗用时间、结果的可信度等。
阻力预测是船舶设计的重要环节,依靠船模试验的阻力预测周期较长,费用高昂。依靠数值模拟的阻力预测精度难以得到保证,难度也较大。因此,在船舶设计前期寻找一种既能快速估算船体阻力,又能保证一定精度的预测方式必要且有意义。基于此,本文介绍多种基于回归分析的船体阻力预测方法,通过计算4种国际标准船模,集中讨论多种预测方法在阻力计算中的精度及适用性,对船舶阻力估算起一定的借鉴和参考作用。
1 阻力预测方法 1.1 排水型船舶排水型船舶的阻力预测方法包括Holtrop法、Compton法、Fung法、van Oortmerssen法、Series 60法以及Wyman法。
Holtrop法的估算公式如下[9]:
| $ {R}_{t}={\left(1+k\right)R}_{f}+{R}_{w}+{R}_{b}+{R}_{app}+{R}_{tr}+{R}_{a}。$ | (1) |
式中:Rf和Rw分别为摩擦阻力和兴波阻力;(1+k)为形状因子;Rb为球鼻艏阻力;Rapp为附体阻力;Rtr为方尾阻力;Ra为修正因子。
Holtrop法给出了式(1)中每个参数的回归公式,综合回归公式可以总结出总阻力的一般函数表达式:
| $ {R}_{t}=f\left(L,B,T,\mathrm{\Delta },{C}_{b},{C}_{p},{C}_{m},{L}_{cb},{A}_{BT},{h}_{B},{A}_{T},{S}_{app}\right) 。$ | (2) |
早期的Holtrop公式只能估算较低傅汝德数船型的阻力,而当估算Fn>0.5的船型时会出现不准确的现象。在后来加入了高速船型的试验数据,该公式的适用范围扩展到了0.55以上。而后又在该基础上引进了Lambda系数:1.446Cp−0.03L/B,认为只有Lambda系数低于一定范围时的船型才适合使用Holtrop法。
总的来说,通过Holtrop公式可以看出,Holtrop法适用于带有球鼻艏和方尾的船型,可用于预测杂货船、渔船、拖船、集装箱船和护卫舰的阻力。
Compton法适用于典型的海岸巡逻、训练或休闲摩托艇型船体形式的阻力预测,其中方尾处于在排水和半滑行状态。Fung法与Compton法类似,同样适用于方尾排水型船舶的阻力预测,区别在于Fung公式中的船舶主尺度通常比Compton法的更大。van Oortmerssen法用于估算拖网渔船和拖船等小型船舶的阻力。Series 60法和Wyman法用于估算单螺旋桨货船的阻力。
1.2 细长体理论细长体理论(slender body method)是一种数值方法,通过计算波系的能量求解兴波阻力[10]。应用细长体理论进行兴波阻力预测时需要作以下假设:
1)理想流体,无粘性,不可压缩,运动无旋;
2)微幅波,不计表面张力;
3)船体在自由液面上作稳定恒速运动。
基于Michell积分[11],细长体方法的积分方程如下:
| $ {R}_{w}=\frac{4\rho {g}^{2}}{{\text{π}} {v}^{2}}\int_{ 1 }^\infty \left({I}^{2}+{J}^{2}\right)\frac{{\lambda }^{2}}{\sqrt{{\lambda }^{2}-1}}{\rm{d}}\lambda,$ | (3) |
| $ I=\int_{ 0 }^\infty \int_{ - \infty }^\infty f\left(x,z\right){e}^{\frac{-{\lambda }^{2}gz}{{v}^{2}}}\frac{{\rm{cos}}\lambda gx}{{v}^{2}}{\rm{d}}x{\rm{d}}z,$ | (4) |
| $ J=\int_{ 0 }^\infty \int_{ - \infty }^\infty f\left(x,z\right){e}^{\frac{-{\lambda }^{2}gz}{{v}^{2}}}\frac{{\rm{sin}}\lambda gx}{{v}^{2}}{\rm{d}}x{\rm{d}}z,$ | (5) |
| $ \lambda =\frac{m{v}^{2}}{g} 。$ | (6) |
式中:ρ为流体密度;g为重力加速度;v为来流速度;m为常数;x、z为积分变量;I、J、λ为中间变量。
细长体方法将船体的湿表面积离散为若干四边形面元。面元的源强为:
| $ \sigma =\frac{{v}_{x}}{2 \text{π} }\frac{{\rm{d}}y}{{\rm{d}}x}\cdot {S}_{0}{'},$ | (7) |
式中:
KCS是一艘由韩国KRISO(Korea Research Institute of Ship and Ocean Engineering)设计的现代集装箱船型,具有详细的试验数据。KCS属于肥大型船,几何模型如图1所示,几何参数如表1所示。设计工况为航行速度2.196 m/s(FnL=0.26)。

|
图 1 KCS船舶几何模型 Fig. 1 Parameters of KCS |
|
|
表 1 KCS船舶几何参数 Tab.1 Geometric parameters of KCS |
KCS属于排水型肥大船,带有一个较大的球鼻艏和巡洋舰尾。从船型上看,Holtrop法、Compton法、Fung法以及Wyman满足KCS船型要求,因此可以初步筛选出阻力预测方法。图2为Holtrop法、Compton法、Fung法以及Wyman法计算得到的阻力与速度曲线。可知,4种预测方法的阻力值均随航速的增加而增大。其中,Wyman法的阻力值增幅最大。Fung法的增幅最小。Holtrop和Fung的阻力曲线十分贴近,两者的计算结果相差不大。Compton阻力曲线出现了2个凸点,分别位于速度2.5 m/s和3.3 m/s处。阻力曲线的随航速走势在经过速度2.5 m/s后有所缓慢,经过速度3.3 m/s后突然升高。Wyman阻力曲线随航速稳步升高,且在整个航速范围内阻力值均大于其余3种方法。
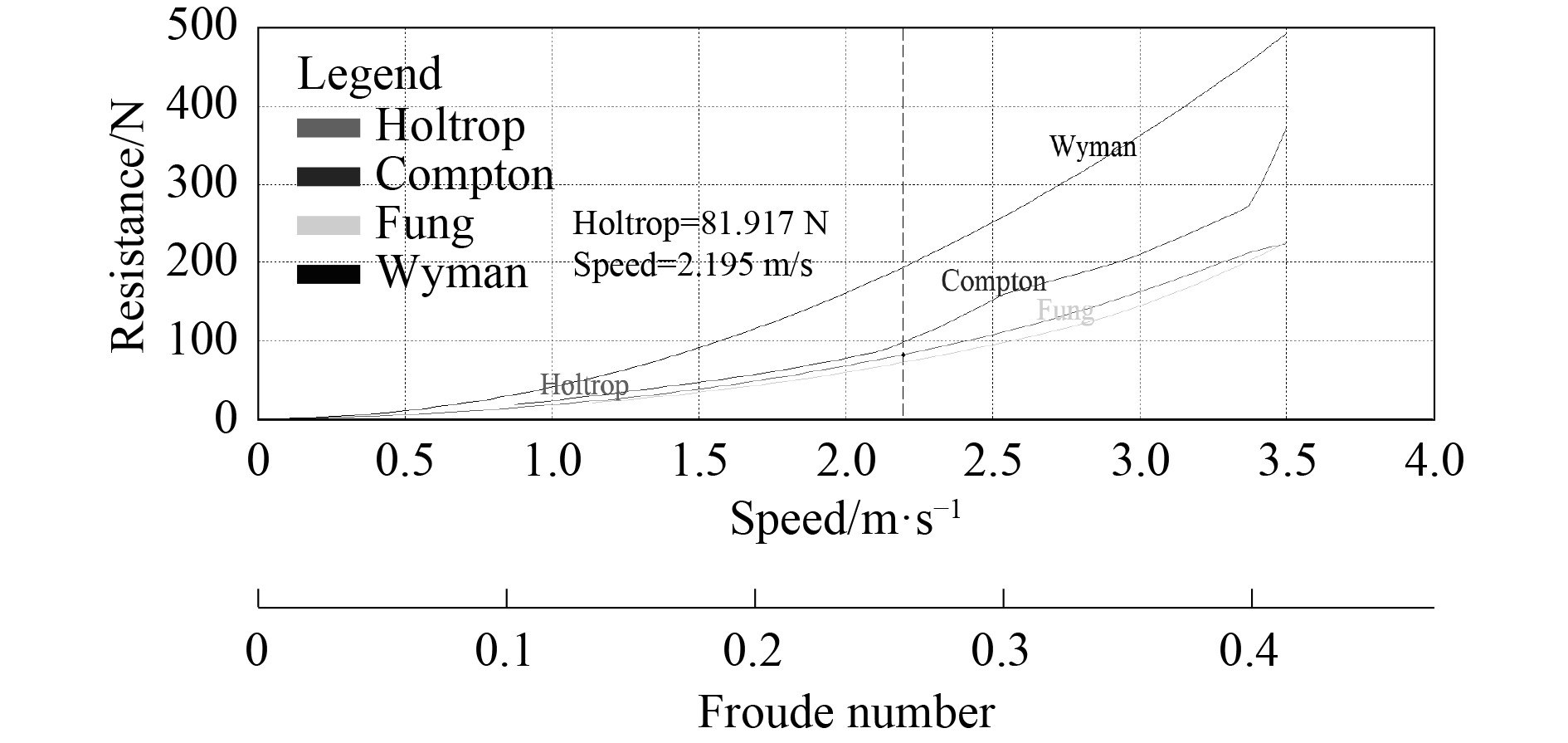
|
图 2 KCS阻力与速度曲线 Fig. 2 KCS resistance and speed curve |
图3为4种预测方法计算得到的功率与速度曲线,同样可以在Graph窗口中查看。HULLSPEED给出的功率计算是阻力、速度和效率的乘积,即P=R×V/η,功率的大小和阻力、航速以及设定的效率有关、不同预测方法的航速和效率完全相同,因此功率的变化只取决于阻力的计算值。功率曲线的走势和阻力曲线完全一致。
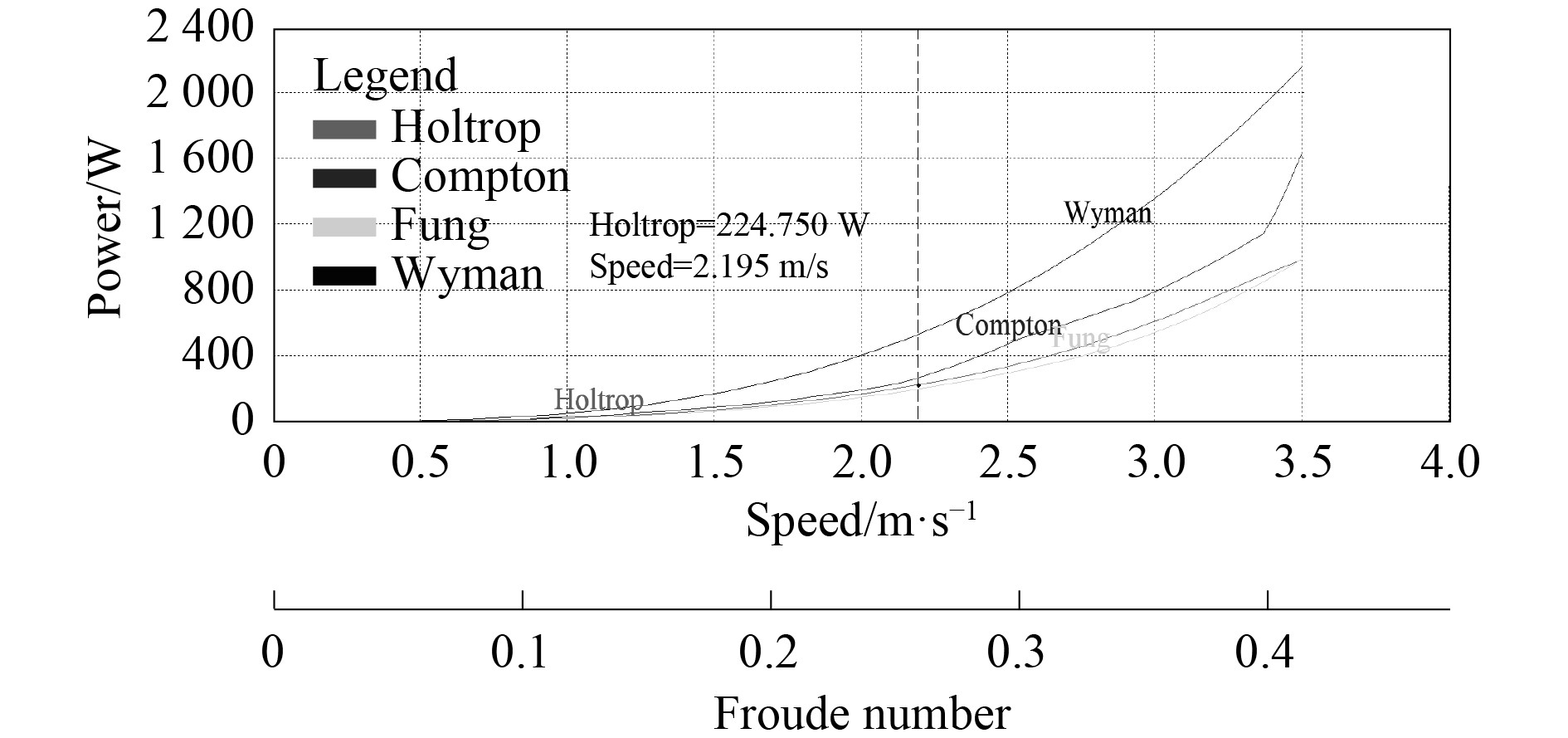
|
图 3 Fn=0.297的RAOs曲线 Fig. 3 RAOs curves with Fn=0.297 |
4种方法在设计航速FnL=0.26的总阻力系数计算结果如表2所示。可知,与试验值[13-14]相比,Holtrop法的误差最小,为−4.196%,Wyman法的误差最大,为−130.533%。Compton法和Fung法的计算结果比价接近,两者误差均在20%以内。在应用Holtrop法计算阻力时,虽然KCS船体的参数有2个超过了Holtrop法的有效范围(分别是船宽和吃水),但有多达13个船体参数参与到了Holtrop法的回归计算,其中除了常规的船体参数外,还有多种与球鼻艏相关的参数,如球鼻艏横剖面面积等,因此Holtrop法的阻力值最符合试验值,计算精度最高。
|
|
表 2 KCS船在FnL=0.26的总阻力系数比较 Tab.2 Comparison of total drag coefficients with Fnl=0.26 |
应用Fung法计算KCS阻力法时,有3个船体参数超过了Fung法的有效范围,有12个船体参数参与了回归计算;应用Compton法计算KCS阻力法时,有4个船体参数超过了Fung法的有效范围,有6个船体参数参与了回归计算;Wyman法只有3个参数参与了计算。3种方法的计算精度分别是:Fung法最高,Compton法次之,Wyman法最低。由此可知,在符合船型的前提下,船体参数的参与越多、越符合预测方法的适用范围,则计算精度越高。
图4为基于细长体理论计算的自由液面结果等,与CFD和试验结果进行的对比。可以看出,与试验及CFD结果相比,细长体理论得到的波形和试验测量的波形吻合程度良好,细长体理论可以较精确地捕获凯尔文波,只有在船首处的波浪高度明显偏低。这是由于KCS船型加装了一个肥大的前伸型球鼻艏,该结构会使船体首部水线的坡度有明显减小,导致船首波的陡直程度有所下降。细长体理论对于该现象的捕捉能力明显不足,但整体而言,细长体理论计算得到的凯尔文波符合试验情况。
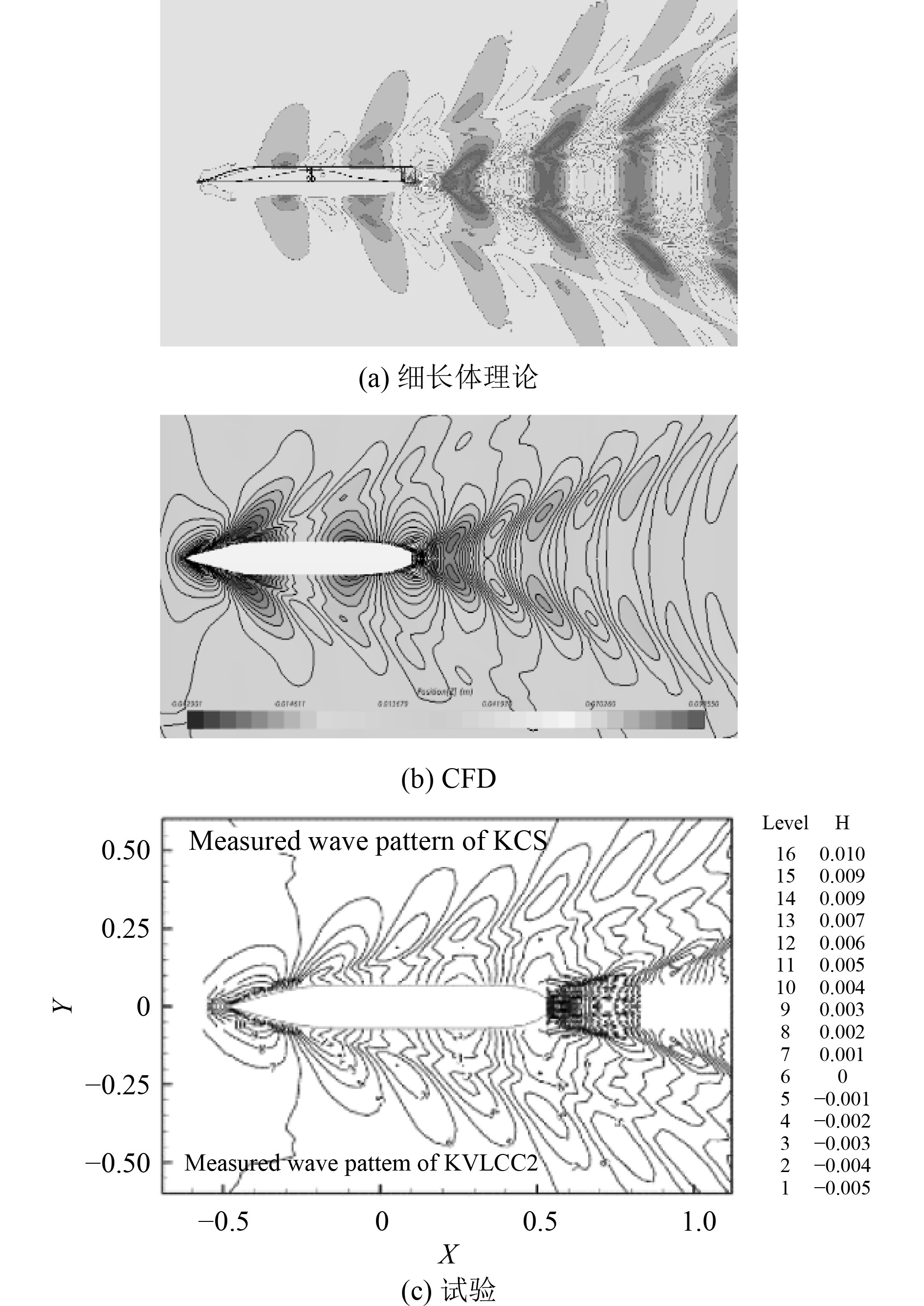
|
图 4 设计工况下的自由液面对比 Fig. 4 Free liquid surface comparison under design conditions |
KVLCC2是一艘由韩国KRISO设计的现代油船,具有详细的试验数据。KVLCC2船模的球鼻艏外形较KCS小,带有更多U形船尾框架线,同样属于肥大型船。KVLCC2船模多用于船舶操纵性的试验验证,如深水及浅水中的斜航运动研究、平面运动机构试验与流场测量实验研究等。几何模型如图5所示,几何参数如表3所示。设计工况为航行速度1.047 m/s(FnL=0.142)。

|
图 5 KVLCC2船舶几何模型 Fig. 5 Model of KVLCC2 |
|
|
表 3 SA船舶几何参数 Tab.3 Geometric parameters of SA |
KVLCC2与KCS在船型特征上有一定相似,同属于排水型肥大船。KVLCC2的球鼻艏较KCS小,船尾带有更多U形框架线。结合KCS的阻力预测结果可知,Holtrop法对肥大船的预测效果较好。此外,用于估算小型船舶阻力的van Oortmerssen法和用于估算单螺旋桨船的Series 60法同样适用于KVLCC2的船型参数。因此可以初步筛选出阻力预测方法。
图6为Holtrop法、van Oortmerssen法以及Series 60法计算得到的阻力与速度曲线。可知,当FnL<0.1时,3种预测方法的阻力值相差不大,FnL>0.1时,3种预测方法的阻力值相差明显。其中,Holtrop阻力曲线的上升幅度和趋势明显大于另外2种方法。van Oortmerssen和Series 60的阻力曲线在FnL =[0.13,0.17]的区间几乎重合,说明2种方法的计算规律在该航速区间内具有高度相似性。在FnL>0.17后,van Oortmerssen阻力曲线后快速上升。
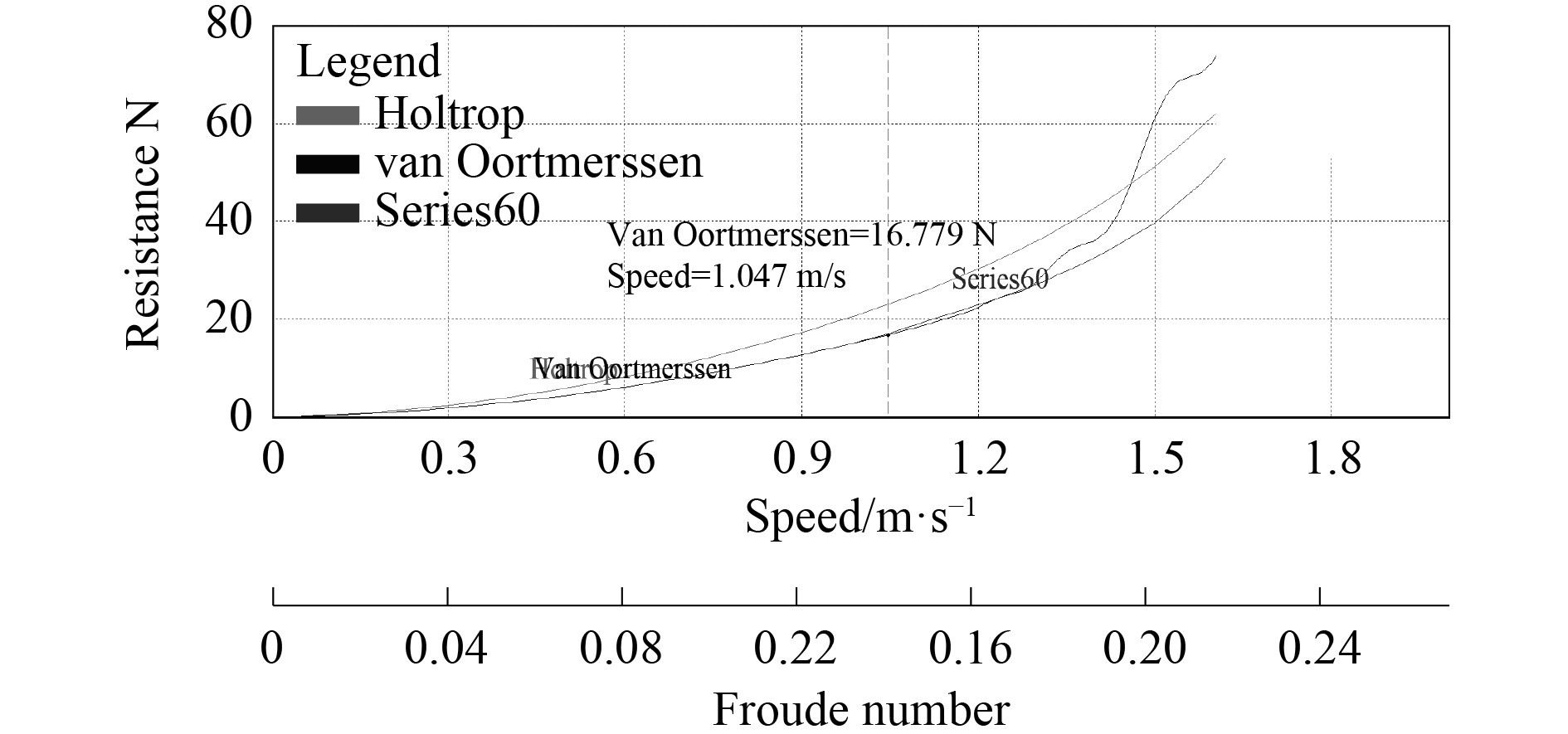
|
图 6 KVLCC2阻力与速度曲线 Fig. 6 KVLCC2 resistance vs Speed Curve |
4种方法在设计航速FnL=0.142的总阻力系数计算结果如表4所示。可知,与试验值[14]相比,van Oortmerssen法和Series 60法的误差最小,分别为5.716%和7.186,Holtrop法的误差最大,为44.894%。虽然KVLCC2的船体参数均在Holtrop法的有效范围内,但Holtrop法的计算精度仍不如van Oortmerssen法和Series 60法,说明Holtrop法在计算超大型油船阻力上的能力明显不如van Oortmerssen法和Series 60法。
|
|
表 4 KVLCC2设计航速FnL=0.142的总阻力系数比较 Tab.4 Comparison of KVLCC2 total drag coefficients with FnL=0.142 |
综合KCS和KVLCC2的阻力估算结果可知,基于回归分析的阻力预测方法可以完成常规排水型船舶的阻力估算。船型特征是选择阻力预测方法的首要因素。只有选择了适合该船型的预测方法,阻力估算的精度才得以保证。Holtrop法在计算集装箱船阻力上的能力较强,van Oortmerssen法和Series 60在计算油船阻力上的能力较强。在符合船型的前提下,船体参数的参与越多、越符合预测方法的适用范围,则计算精度越高。
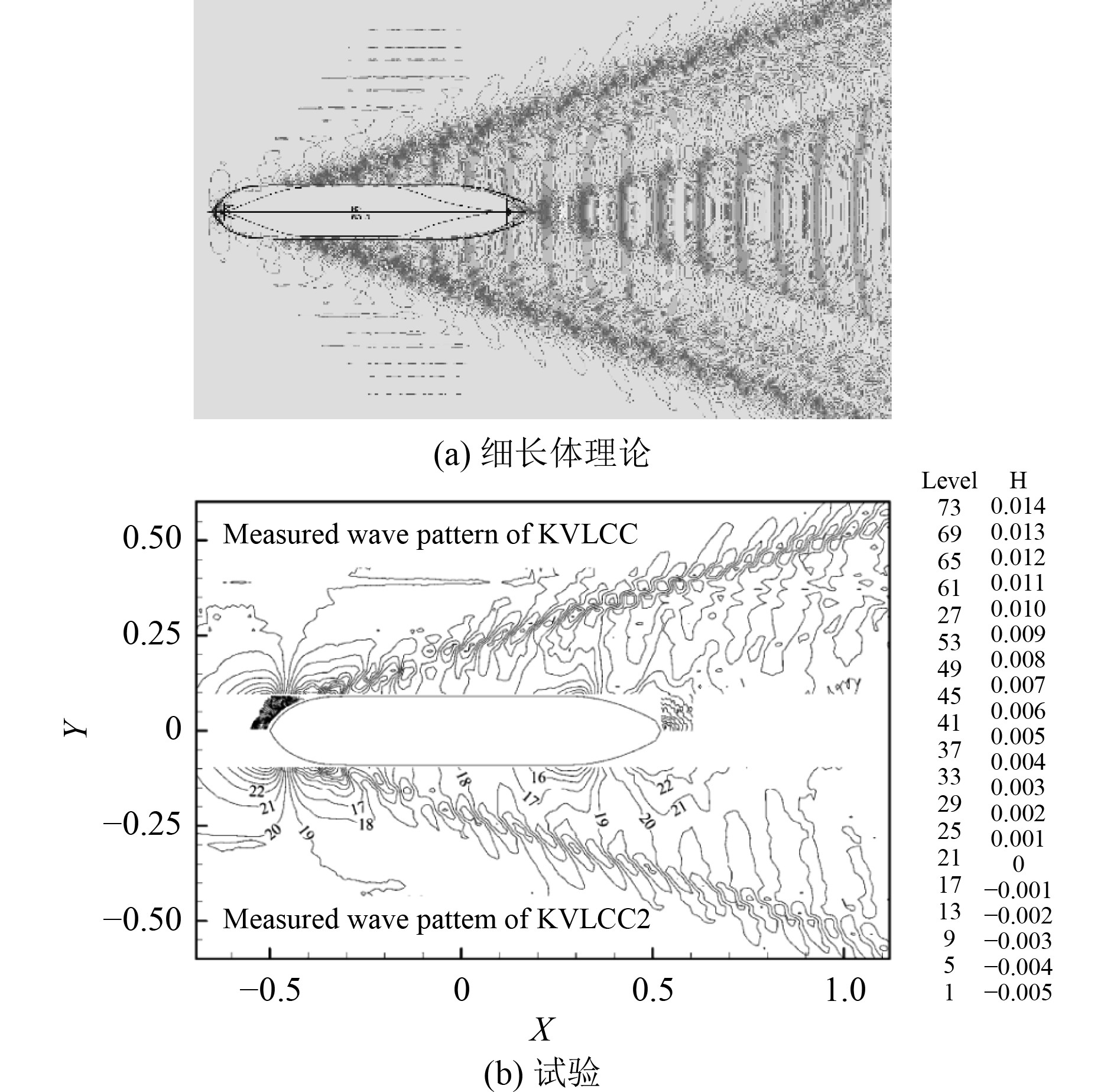
图7为细长体理论计算的自由液面结果及同时与试验结果的对比。可以看出,细长体理论得到的波形和试验测量的波形吻合程度较好。对于低速肥大型油船来说,兴波阻力占总阻力的比重较小。KVLCC2的傅汝德数为0.142,因此产生了波高相对较小的短波。由于KVLCC2的航速比KCS低,因此其凯尔文角也较KCS大,且船首与船尾产生的波浪多以横波和散波为主。KVLCC2的设计吃水线同样位于方尾上方,但显然没有像KCS那样形成“干尾梁”。
|
图 7 KVLCC2设计航速下的自由液面对比 Fig. 7 Free liquid surface comparison under design conditions of KVLCC2 |
Wigley船型是国际上通用的一种数学船型,有大量计算数据便于比较。该船型是由一族简单的抛物线组成,型值可由以下数学公式得出:
| $ y=2B\left[\frac{1}{4}-{\left(\frac{x}{{L}_{pp}}\right)}^{2}\right]\left[1-{\left(\frac{z}{d}\right)}^{2}\right] 。$ | (13) |
其中:LPP为垂线间长;B为最大船宽;d为吃水;x、y、z分别为空间三维点坐标。d/LPP=0.0625;B/LPP=0.1。吃水线以下的外形由船体表面方程给出,几何模型如图8所示,几何参数如表5所示。

|
图 8 Wigley几何模型 Fig. 8 Model of Wigley |
|
|
表 5 Wigley船舶几何参数 Tab.5 Geometric parameters of Wigley |
图9为基于HULLSPEED模块计算得到的兴波阻力系数曲线,以及与2种理论方法以及试验结果[15]进行的比较。可知,细长体理论的兴波阻力系数曲线几乎与另外2种理论方法完全重合,说明细长体方法适用于瘦长船型的兴波阻力计算。无论是细长体方法还是另外2种理论方法,兴波阻力系数的计算均比试验结果大,原因可能在于理论方法通过计算首尾波系的能量进而计算出兴波阻力的方式对于首尾波系之间兴波干扰的计算能力不足,而这种干扰可能是有利的,一定程度会减小船体的兴波阻力。

|
图 9 Wigley船兴波阻力系数曲线对比 Fig. 9 Comparison of curves of wave-making resistance coefficients of Wigley |
兴波阻力Rw由两部分组成,一部分是横波和散波所产生的兴波阻力,另一部分是横波发生干扰后的兴波阻力。兴波阻力系数曲线上出现的凸点,称为波阻峰点,此时船首横波与船尾横波发生不利干扰,兴波阻力增大;兴波阻力系数曲线上出现的凹点,称为波阻谷点,表明该航速下船首横波与船尾横波发生有利干扰,此时兴波阻力有所减小。由图9可知,当Fn<0.2时,Wigley船的兴波阻力系数值很小,说明低速时兴波阻力成分较小。当0.2<Fn<0.4时,Wigley船的兴波阻力系数曲线在快速上升的同时出现多个波阻峰点和波阻谷点,说明此时Wigley船的船首横波与船尾横波发生了复杂的兴波干扰。当0.4<Fn<0.5时,兴波阻力系数曲线迅速上升至最大值,此时兴波阻力在总阻力中所占比例较大。当Fn>0.5,兴波阻力系数随Fn增大而减小。
图10为细长体理论计算的自由液面结果,同时与理论结果进行对比。可以看出,细长体理论得到的波形和CFD波形吻合程度较好。船舶在静水中以定常速率沿直线航行时存在2个波系横波和散波,波系边界与船舶航向所夹的波浪半角为凯尔文角。横波的波峰大致上垂直于船舶的航线,与散波相比其波长更长。船尾后的波浪特征可以将其看做不同方向的多个规则线性长波峰的叠加来解释。船行波沿凯尔文角的方向衰减最慢,在船舶的远端破碎成细小且相邻的多个波。

|
图 10 Wigley船的自由液面对比 Fig. 10 Free liquid surface comparison of Wigley |
NPL圆舭艇是由原英国国家物理实验室(NPL)主持设计的一系列高速排水型快艇,试验内容相当广泛,涉及船舶阻力与推进、操纵性和耐波性等。几何模型和横剖线如图11所示,几何参数如表6所示。

|
图 11 NPL圆舭艇几何模型 Fig. 11 Model of NPL |
|
|
表 6 NPL圆舭艇几何参数 Tab.6 Geometric Parameters of NPL |
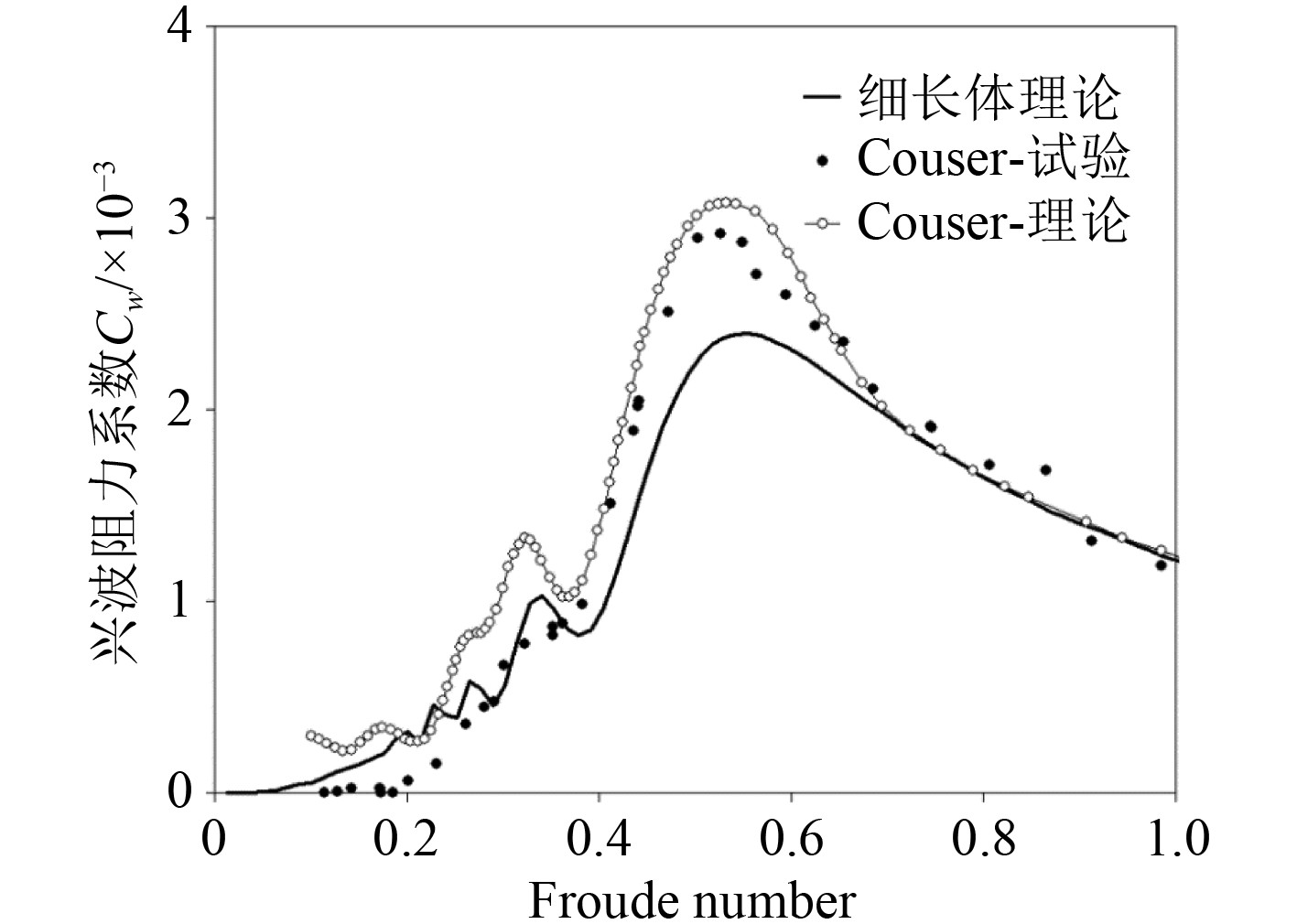
图12为基于细长体理论计算得到的NPL船兴波阻力系数曲线及同时与Couser理论方法和Couser试验结果[16]进行的比较。可知,在Fn<0.4的低速和Fn>0.7的高速范围内,HULLSPEED的计算值与试验值几乎重合,而在0.4<Fn<0.7的过渡范围,HULLSPEED的计算值偏低。这是由于应用细长体方法时,在NPL船的方尾后添加了虚拟附体。虚拟附体可以较好地模拟低速条件下方尾后的湍流粘性尾迹以及高速条件下水从方尾处快速释放时产生的气隙。中高速范围方尾后的湍流较为复杂,既有粘性作用也有少部分气隙产生,因此细长体方法的精度有所下降。除此之外,试验的条件包含模型的自由升沉和纵倾,Couser的理论结果也包含了试验中实测的升沉和纵倾,因此与试验结果非常吻合。应用细长体理论时使用一个固定的吃水线,在一般情况下每个速度下的船体姿态是未知的,这也会产生一定的误差。但总的来说,在整个Fn范围,细长体理论能够较好地计算瘦长船型和方尾船的兴波阻力系数。
|
图 12 NPL船兴波阻力系数曲线对比 Fig. 12 Comparison of Curves of Wave-making Resistance Coefficients of NPL |
同Wigley船型相比,NPL船的兴波阻力系数曲线在整个Fn范围内的走势基本一致,且同样在Fn=0.5的附近产生兴波阻力系数的最大值。区别在于NPL船的兴波阻力系数普遍比Wigley船小。两者均属于瘦长型船体,最大的区别在于NPL船添加了方尾。高速水流沿着方尾边缘一直延伸到尾后,其作用相当于增加了船体的有效长度,有利于减小兴波阻力。方尾的这种作用通常称为虚长度作用。在应用细长体理论时添加虚拟附体可以有效地模拟虚长度作用。
综合Wigley船型和NPL船型的计算情况可知,细长体方法可以有效模拟瘦长型船体的兴波阻力系数。适当添加虚拟附体能够增加细长体方法的计算精度。
3 结 语本文采用多种阻力预测方法对KCS船舶、KVLCC2船舶、Wigley船型以及NPL圆舭艇的阻力进行估算,包括Holtrop法、Compton法、Fung法、van Oortmerssen法、Series 60法、Wyman法以及细长体理论。结果表明,基于回归分析方法计算常规排水型船舶阻力和基于细长体方法计算瘦长船型和方尾船阻力的方案可行。船型特征是选择阻力预测方法的首要因素,只有选择了适合该船型的预测方法,阻力估算的精度才得以保证。适当添加虚拟附体能够增加细长体方法的计算精度。细长体理论计算的自由面波形结果基本令人满意。
| [1] |
罗良. 基于一维方法和三维方法的模型尺度及实船尺度船舶阻力预报[J]. 舰船科学技术, 2022, 44(6): 18-21. LUO Liang. Model size and full-scale ship resistance prediction based on one-dimensional and three-dimensional methods[J]. Ship Science and Technology,, 2022, 44(6): 18-21. DOI:10.3404/j.issn.1672-7649.2022.06.004 |
| [2] |
贺妍. 基于CFD的穿浪双体船水动力性能分析[D]. 大连: 大连理工大学, 2021.
|
| [3] |
宋科委, 郭春雨, 孙聪, 等. 实尺度船舶阻力计算及尺度效应研究[J]. 华中科技大学学报(自然科学版), 2021, 49(6): 74-80. SONG Kewei, GUO Chunyu, SUN Cong, et al.. Calculation of real scale ship resistance and research on scale effects[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(6): 74-80. DOI:10.13245/j.hust.210614 |
| [4] |
邱鹏, 何钰璋, 李国诚. 船舶阻力数值计算研究[J]. 中国水运, 2021(1): 121-123. DOI:10.13646/j.cnki.42-1395/u.2021.01.045 |
| [5] |
刘飞. 基于CFD方法的破损船舶阻力预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2021.
|
| [6] |
李浅洋, 胡义, 程洪凯. 基于VB. Net的船舶阻力预报集成化研究[J]. 船舶工程, 2019, 41(12): 58-63. |
| [7] |
黄丽, 张瑞. 基于CFD的船舶阻力数值模拟[J]. 广船科技, 2018, 38(4): 15-18. DOI:10.3969/j.issn.2095-4506.2018.04.003 |
| [8] |
钟铮. 基于Web的船舶阻力教学网络信息远程监控系统设计[J]. 舰船科学技术, 2019, 41(4): 220-222. |
| [9] |
王楠, 周旭. 改进的Holtrop船舶阻力估算[J]. 船海工程, 2019, 48(4): 34-37. DOI:10.3963/j.issn.1671-7953.2019.04.008 |
| [10] |
杨显原, 吴家鸣, 陈宇庆. 基于兴波干扰的三体船构型数字化优化方法[J]. 船舶工程, 2017, 39(S1): 53-57. DOI:10.13788/j.cnki.cbgc.2017.S1.053 |
| [11] |
MICHELL J H. The wave-resistance of a ship[J]. Philosophical Magazine (Series 5), 1898, 272(45): 106-123. |
| [12] |
COUSER P R, WELLICOME J F, MOLLAND A F. An Improved Method for the Theoretical Prediction of the Wave Resistance of Transom-Stern Hulls Using a Slender Body Approach[J]. International Shipbuilding Progress, 1998, 444(45): 331-349.
|
| [13] |
LARSSON L, STERN F, BERTRAM V. Benchmarking of computational fluid dynamics for ship flows: the gothenburg 2000 workshop[J]. Journal of Ship Research, 2003, 47(1): 63-81. DOI:10.5957/jsr.2003.47.1.63 |
| [14] |
KIM W J, VAN S H, KIM D H. Measurement of flows around modern commercial ship models[J]. Experiments in Fluids, 2001, 31(5): 567-578. DOI:10.1007/s003480100332 |
| [15] |
COUSER P R, WELLICOME J F, MOLLAND A F. An improved method for the theoretical prediction of the wave resistance of transom-stern hulls using a slender body approach[J]. International Shipbuilding Progress, 1998, 45(444): 331-349. |
| [16] |
COUSER, PATRICK. An investigation into the performance of high-speed catamarans in calm water and waves[D]. University of Southampton, 1996.
|
 2023, Vol. 45
2023, Vol. 45
