2. 上海市公共建筑和基础设施数字化运维重点实验室, 上海200240
2. Shanghai Key Laboratory for Digital Maintenance of Buildings and Infrastructure, Shanghai 200240, China
现阶段船舶相关规范在对船舶与海洋结构物进行结构设计和强度评估时,采用的是许用应力法[1]。许用应力法只采用了1个安全系数K来确定结构的可靠程度,而建筑钢结构设计标准经历了从许用应力法,到以概率为基础的极限状态设计法,再到以非线性分析计算极限强度为基础的高等分析法的发展历程[2]。高等分析法是考虑结构缺陷直接计算极限强度的设计方法,该方法在建筑钢结构领域已经得到了应用,这也是船舶结构设计必然的发展趋势。初始缺陷的选取对于高等分析法计算极限强度至关重要,对于缺陷敏感结构(如板、壳等),不同的初始缺陷形态会对极限强度计算结果产生很大影响。与建筑钢结构类似,船舶结构中初始缺陷包括凹陷、初始变形和残余应力等[11],目前考虑结构初始缺陷的通用做法是通过施加结构整体位移缺陷来模拟结构中存在的各种缺陷形式。
加筋板是用来建造船体结构的板材,是船体结构的重要组成部分[3-4]。国内外学者针对加筋板极限强度展开了大量研究,但针对初始缺陷具体形态的研究较少。Paik等[5]利用有限元软件Ansys研究了双轴压缩和侧压力作用下加筋板结构极限强度;Tanaka等[6]和Smith等[7]进行了一系列的试验测试了加筋板的极限强度;杨帆等[8]利用Abaqus的Risks弧长法计算加筋板的极限强度并与试验结果比较,指出采用有限元弧长法能较为准确地计算加筋板的极限强度;刘春正等[9]通过引入双三角级数形态的初始缺陷进行了加筋板的稳定性分析。目前,加筋板有限元计算模型中引入初始缺陷的方法主要有2种:1)普遍采用一阶屈曲型初始缺陷,即先进行特征值屈曲分析,取一阶屈曲模态作为结构的初始缺陷形态;2)瘦马型初始缺陷[10],即利用三角级数变形公式,对理想结构的每个节点直接施加变形作为初始缺陷形态。这些做法都是采用施加位移缺陷来模拟加筋板结构中的各种缺陷形式。对于加筋板结构,特征值分析求得的屈曲模态往往以局部变形为主。这种初始缺陷选取方法只能体现加筋板局部的缺陷,难以表达结构的整体缺陷分布,以这种方法计算往往会高估加筋板结构的极限强度。
本文借鉴建筑钢结构[11-12],将失稳模态型初始缺陷引入到船舶结构加筋板的极限强度分析中,失稳模态型初始缺陷能够相对准确地模拟加筋板结构的整体位移缺陷,从而较完善地考虑结构中存在的凹陷、初始变形和残余应力等各种初始缺陷。对加筋板不同初始缺陷形态下的极限强度进行分析并与试验结果对比,验证了失稳模态型初始缺陷引入方式在加筋板极限强度计算中的可行性与有效性。相关研究进一步表明[13],一阶屈曲模态型初始缺陷不能反映舱段的整体缺陷,计算得到的极限强度存在较大偏差,而失稳模态型初始缺陷适用于舱段结构极限强度分析。应用考虑失稳模态型初始缺陷引入方式,进行31个单一参数变量加筋板的极限强度有限元计算,探究板厚、加强筋高度及厚度对加筋板极限强度的影响,给出优化设计建议。
1 考虑初始缺陷的加筋板极限强度计算 1.1 考虑不同初始缺陷形态的计算过程一阶屈曲型初始缺陷已在加筋板的极限强度分析中普遍采用。这种方法是将特征值分析得到的一阶屈曲模态作为结构初始缺陷形态,具体实现过程为:
1)对理想结构进行线性特征值分析,得到结构的一阶屈曲模态;
2)限制最大缺陷值,将一阶屈曲模态作为位移形态,施加到理想结构上作为初始缺陷;
3)获得施加在理想结构上的初始缺陷,进行后续的非线性分析。
在空间网架网壳结构中,许多学者针对不同的初始缺陷形态进行研究。其中一种初始缺陷施加方法为一致模态法[12],这种方法是将最低阶屈曲临界点所对应的位移增量模式作为结构的最低价屈曲模态,进而模拟初始缺陷分布,具体实现过程为:
1)利用弧长法对理想网架网壳开展一次完整的静力非线性全过程分析;
2)对屈曲前、后2个邻近状态的位移形态做差值;
3)获得施加在理想网架网壳结构上的节点位移模式,限制最大缺陷值,进行后续非线性分析。
参考一致模态法思路,将理想加筋板进行非线性分析得到的失稳模态作为初始缺陷形态,提出一种失稳模态型初始缺陷形态,具体实现过程为:
1)利用弧长法对理想加筋板开展一次完整的静力非线性全过程分析,得到理想加筋板极限强度下的失稳模态;
2)将此失稳模态作为初始缺陷形态,限制最大缺陷值,引入到理想加筋板中;
3)进行后续的非线性分析得到极限强度结果。
计算中需要保证不同初始缺陷形态引入理想加筋板的最大缺陷值相同,统一取引入理想加筋板的最大缺陷值为
以Tanaka系列试验加筋板[6]为对象建立分析模型。采用Ansys软件建立上述2种不同初始缺陷形态的有限元分析模型,将计算结果与部分试验数据进行对比分析,探究不同初始缺陷形态下加筋板的极限强度。计算中采用shell181单元,单元长度控制在30~40 mm;假定板的材料是理想弹塑性,忽略材料的应力强化作用,以von Mises屈服准则作为材料的屈服准则,材料屈服极限强度为σy= 315 MPa,弹性模量E=2.058×105 MPa,泊松比ν=0.3;2种初始缺陷形态的节点最大变形为
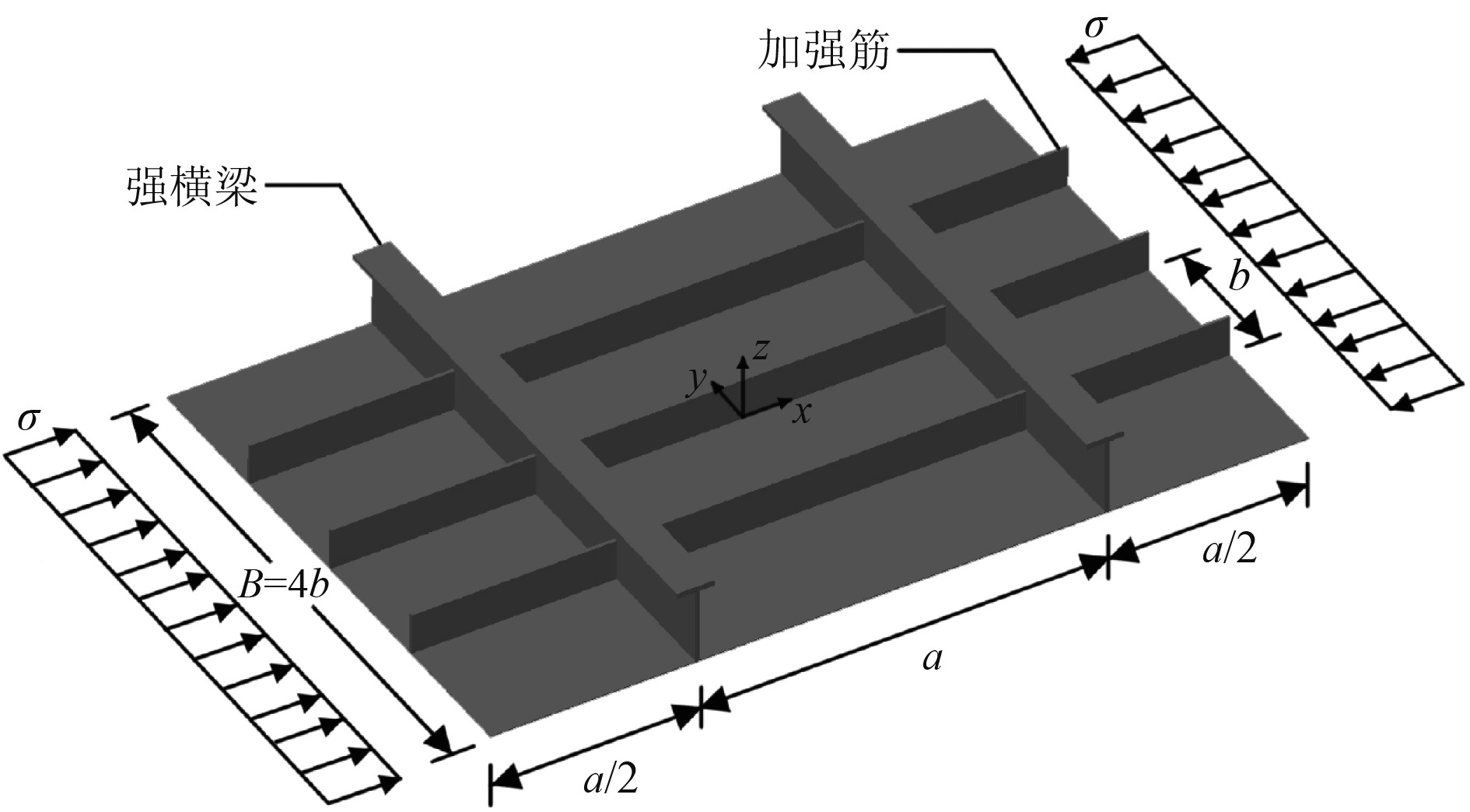
如图1所示,加筋板由纵梁和强横梁共同支撑,纵梁位于图示的纵向最外侧,间距为
|
图 1 加筋板示意图 Fig. 1 Schematic diagram of stiffened panel |
1)2个长边(
2)四周边界均约束转动位移
3)2个短边(
4)2个短边中点
5)强横梁模型以边界条件约束代替,强横梁在板上的节点保持
有限元模型边界条件和荷载施加情况如图2所示。

|
图 2 有限元模型边界条件和荷载施加情况 Fig. 2 Boundary conditions and load application of finite element model |
首先,将考虑一阶屈曲型初始缺陷与考虑失稳模态型初始缺陷的极限强度计算结果和Tanaka系列加筋板试验结果进行比对,结果见表1。以D0A板为例,一阶屈曲型与失稳模态型2种不同初始缺陷形态如图3所示。
|
|
表 1 2种方法计算结果与试验结果的对比 Tab.1 Comparison between the calculated results of the two methods and the experimental results |
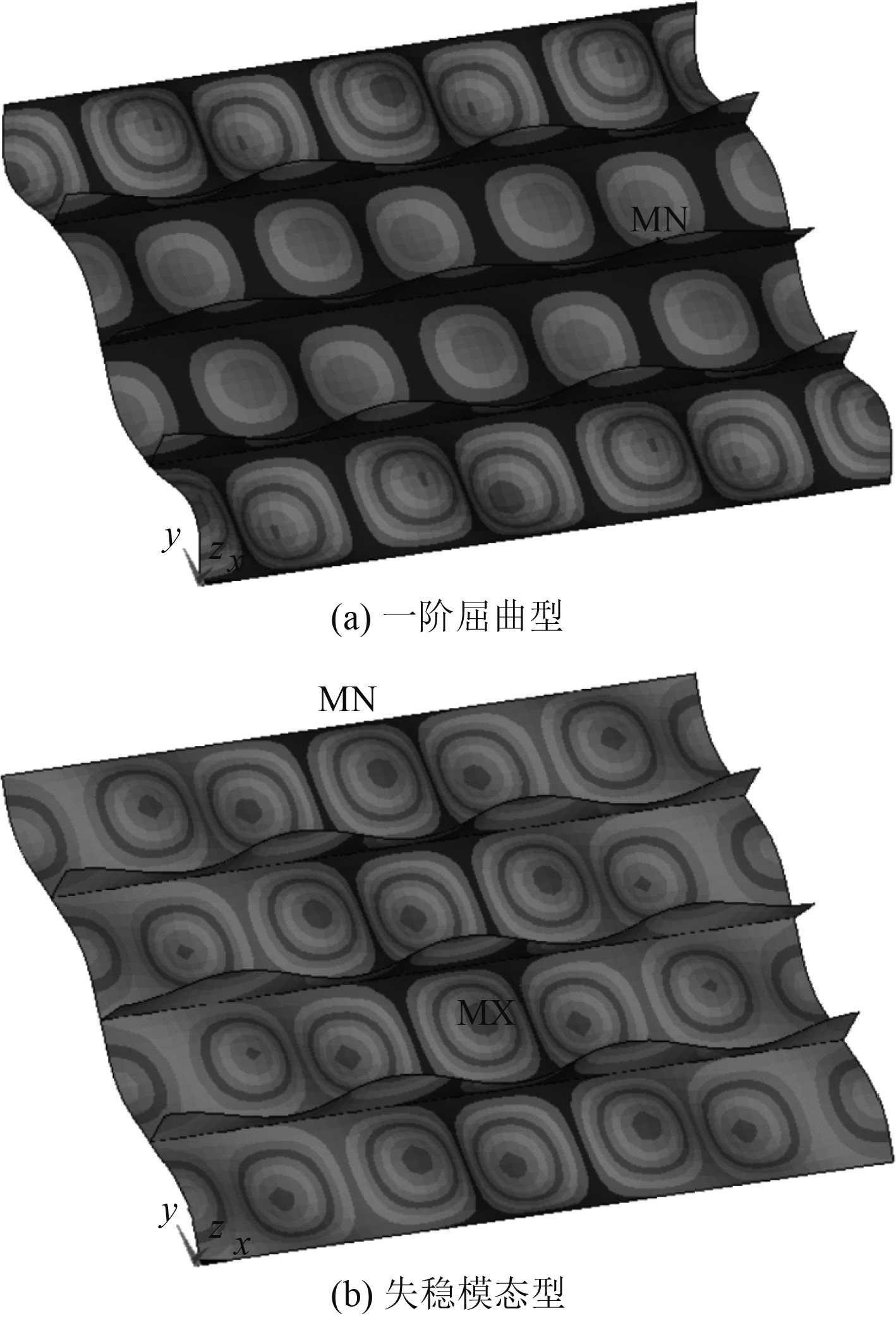
|
图 3 D0A板的2种不同初始缺陷形态 Fig. 3 Two different initial deflection forms of D0A panel |
通过表1数据对比可以发现,相比于Tanaka系列试验结果,考虑一阶屈曲型初始缺陷和考虑失稳模态型初始缺陷极限强度计算结果都与试验值接近,且最大误差都在5%以内,验证了有限元模型的正确性。但对于D0A、D1、D2、D3 4块加筋板,考虑失稳模态型初始缺陷的计算结果比考虑一阶屈曲型初始缺陷的计算结果偏低,因此以失稳模态型初始缺陷形态进行加筋板优化设计更利于保证结构安全。
为了进一步验证上述规律,建立25个加筋板模型进行补充分析。计算模型中取a=1 080 mm,b=360 mm,各加筋板其他几何尺寸及极限强度对比结果见表2,其中加筋板模型参数均以Tanaka系列物理实验对象为基准。根据对船体加筋板尺寸的统计,在如下范围内进行加筋板参数的选取[15]:
|
|
表 2 考虑2种不同初始缺陷的极限强度计算结果对比 Tab.2 Comparison of ultimate strength calculation results considering two different initial deflections |
计算结果表明,采用失稳模态型初始缺陷比采用一阶屈曲型初始缺陷得到的极限强度普遍偏低且相差不大。这是由于模型选取的是船体甲板局部加筋板,采用一阶屈曲模态型初始缺陷便可较好反映加筋板局部变形,因而极限强度计算结果与试验结果较为接近。同时,失稳模态型初始缺陷计算结果也与实验结果接近,验证了这种初始缺陷引入方式在加筋板极限强度计算中的可行性与有效性,且其相对于一阶屈曲型初始缺陷计算得到的极限强度更低,更能保证加筋板结构的安全。同时,通过相关研究可知[13],屈曲型初始缺陷无法反映结构整体缺陷,而失稳模态型初始缺陷能较好反映结构整体缺陷,适用于船体舱段的极限强度分析。不论是舱段模型还是加筋板模型,采用失稳模态型初始缺陷得到的极限强度结果都更接近试验结果,建议采用失稳模态型初始缺陷进行加筋板设计以更好地保证结构安全。
2 加筋板极限强度影响参数分析 2.1 分析计算模型采用失稳模态型初始缺陷进行极限强度计算,分析板厚、加强筋高度及厚度对加筋板极限强度的影响。加筋板模型参数同样以Tanaka系列物理实验对象为基准参考建立,采用单一变量法建立如表3所示的31个加筋板有限元计算模型并进行分析[15]:基准模型M0取加筋板参数a=1 080 mm,b=360 mm,t=6 mm,hw=110 mm,tw=10 mm;对加筋板厚度(A组)、加强筋高度(B组)、加强筋厚度(C组)3个影响因素,每组各设置10个对比计算模型(编号1~10);编号相同的模型保证用钢量相同(如A1、B1、C1用钢量同为171.93 kg)。其中计算模型的最小用钢量为171.93 kg,最大用钢量为232.98 kg,用钢量取值间距为6.10 kg,折算到加筋板板厚、加强筋高度、加强筋厚度的取值间距分别为0.25 mm、12 mm、1.09 mm。
|
|
表 3 参数设置及极限强度计算结果 Tab.3 Parameter setting and ultimate strength calculation results |
各模型的参数设置及极限强度计算结果如表3所示,各计算模型的极限强度与用钢量的关系如图4所示。

|
图 4 各计算模型的极限强度与用钢量的关系 Fig. 4 Relationship between ultimate strength and steel consumption |
由图4可知,在相同用钢量标准下,加筋板厚度
由图4可知,在相同用钢量标准下,加强筋高度hw在50~170 mm范围内变化时,随着加强筋高度的增加,加筋板极限强度出现显著增高,但随着高度继续增加,加筋板极限强度反而下降,加强筋的高度影响了加筋板的失稳破坏模式。筋的柔度随加强筋高度 的变大而减小,当下降到0.45左右(模型中取98 mm和110 mm),加筋板极限强度达到同组相对较大值,加筋板承载能力得到较为理想的提高。
对比3条曲线可以得出,编号3、编号4、编号5的用钢量条件下增高加强筋对极限强度的提升效果最好。同时,在编号1、编号2的用钢量条件下,增高加强筋后,加筋板的极限强度得到了显著提升,这是由于失稳模式发生改变。如图5所示,加强筋高度为50 mm时失稳模式为加筋板的整体失稳,加强筋高度为62 mm时失稳模式为加强筋间的板局部失稳[15]。

|
图 5 不同加强筋高度下加筋板的失稳模式 Fig. 5 Failure modes of stiffened panels with different stiffener heights |
由图4可知,在相同用钢量标准下,加强筋厚度tw在4.55~15.45 mm范围内变化时,增厚加强筋可以上提高加筋板的极限强度,但其效果没有增高加强筋的效果明显。而且在加强筋厚度超过11.09 mm(筋的柔度
本文对船体结构加筋板提出一种失稳模态型初始缺陷形态引入方式,并与一阶屈曲型初始缺陷形态引入方式及试验结果对比,验证了失稳模态型初始缺陷引入方式在加筋板极限强度计算中的可行性与有效性。运用失稳模态型初始缺陷引入方式进行了加筋板极限强度的影响参数分析,主要结论如下:
1)最大缺陷值相同时,采用失稳模态型初始缺陷比采用一阶屈曲型初始缺陷得到的加筋板极限承载力更低,建议采用失稳模态型初始缺陷形态进行加筋板极限承载力计算,保证结构的安全。
2)增高加强筋可以提高筋的刚度,显著提高加筋板的极限强度,但加强筋过高会改变加筋板的失稳破坏形式,不利于提高加筋板的极限强度。
3)增厚加强筋可以提高加筋板的极限强度,加强筋厚度达到一定数值时加筋板极限强度增加效果不明显。建议取0.40~0.45作为筋的柔度
4)增厚加筋板可以一定程度上提高加筋板的极限强度,但在合理设计范围内的同等用钢量条件下,增厚加筋板对于极限强度的提升效果不如增高加强筋明显。增高加强筋是提升加筋板极限强度考虑的首要措施,如果想提升极限强度,可以采取增厚加筋板的措施。
| [1] |
中国船级社. 钢质海船入级规范[S]. 2021.
|
| [2] |
钢结构设计标准: GB50017—2017[S]. 北京: 中国建筑工业出版社, 2017.
|
| [3] |
施兴华, 卞璇屹, 钱鹏, 等. 初始缺陷对加筋板结构极限强度的影响研究[J]. 舰船科学技术, 2017, 39(3): 29-35. SHI X H, BIAN X Y, QIAN P, et al. Effect of initial imperfections on the ultimate strength of stiffened panels[J]. Ship Science and Technology, 2017, 39(3): 29-35. |
| [4] |
张涛, 刘土光, 赵耀, 等. 初始缺陷加筋板的屈曲与后屈曲分析[J]. 船舶力学, 2003, 7(1): 79-83. ZHANG T, LIU T G, ZHAO Y. et al. Buckling and post-buckling of imperfect stiffened plates[J]. Journal of Ship Mechanics, 2003, 7(1): 79-83. |
| [5] |
PAIK J K, LEE J M, KO M J. Ultimate shear strength of plate elements with pit corrosion wastage[J]. Thin-Walled Structures, 2004, 42(8): 1161-1176. DOI:10.1016/j.tws.2004.03.024 |
| [6] |
TANAKA Y, ENDO H. Ultimate strength of stiffened plates with their stiffeners locally buckled in compression[J]. Journal of the Society of Naval Architects of Japan, 1988, 164: 456-467. |
| [7] |
SMITH CS. Compressive strength of welded steel ship grillages[J]. RINA Transactions, 1975, 118: 325-359. |
| [8] |
杨帆, 岳珠峰, 李磊. 基于弧长法的加筋板后屈曲特性分析及试验[J]. 应用力学学报, 2015, 32(1): 119-124. YANG F, YUE ZH F, LI L. Analysis and experiment of post-buckling characteristics of stiffened panel under compress load by arc-length method[J]. Chinese Journal of Applied Mechanics, 2015, 32(1): 119-124. |
| [9] |
刘春正, 吴梵, 牟金磊. 含初始缺陷加筋板的稳定性分析[J]. 舰船科学技术, 2017, 39(4): 40-44. LIU CH ZH, WU F, MOU J L. The buckling analysis of the stiffened plate with initial deflection[J]. Ship Science and Technology, 2017, 39(4): 40-44. |
| [10] |
梅佳雪, 杜尊峰, 朱海涛. 船体结构加筋板极限强度的影响因素[J]. 船舶工程, 2021, 43(9): 37-42. MEI J X, DU Z F, ZHU H T. Influencing factors of ultimate strength of stiffened plate of ship structure[J]. Ship Engineering, 2021, 43(9): 37-42. |
| [11] |
范峰, 曹正罡, 马会环, 等. 网壳结构弹塑性稳定性[M]. 北京: 科学出版社, 2015.
|
| [12] |
张明, 侯积英, 支旭东, 等. 初始几何挠度模式对单层球面网壳抗震性能的影响[J]. 振动与冲击, 2021, 40(5): 33-38. ZHANG M, HOU J Y, ZHI X D, et al. Effect of initial geometric imperfection modes on aseismic performance of single-layer spherical reticulated shell[J]. Journal of Vibration and Shock, 2021, 40(5): 33-38. |
| [13] |
张宜杰, 李淇雯, 邱国志, 等. 考虑失稳模态型初始缺陷的船体舱段极限强度分析[J]. 舰船科学技术, 2023, 45(10): 19–22.
|
| [14] |
张晓丹, 杨平. 加筋板在极限压力下的轴向强度研究[J]. 武汉理工大学学报, 2011, 35(2): 305-312. ZHANG X D, YANG P. Ultimate strength of stiffened plate under axial compression[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2011, 35(2): 305-312. |
| [15] |
ZHANG SH M, KHAN IMTAZ. Buckling and ultimate capacity of plates and stiffened panels in axial compression[J]. Marine Structures, 2009, 22(4): 791-808. DOI:10.1016/j.marstruc.2009.09.001 |
| [16] |
ISSC. Report of specialist committee Ⅲ. 1-ultimate strength[S]. 2012.
|
| [17] |
单成巍. 循环载荷作用下船体结构的极限强度非线性有限元分析[D]. 武汉: 武汉理工大学, 2013.
|
 2023, Vol. 45
2023, Vol. 45
