2. 南通中远海运川崎船舶工程有限公司,江苏 南通 226005
2. Nantong Cosco Khi Ship Engineering Co., Ltd., Nantong 226005, China
船舶制造是一个复杂的过程,需要将大量的钢材和其他材料进行组装和装配。焊接结构是将这些材料连接在一起的主要方法之一,焊接结构可以用于连接船体的各个部分,如船体的船板、船底、船舱等。焊接可以提供强大的连接,使船体具有足够的强度和刚度,以应对海上恶劣的环境条件。焊接结构还可以用于连接船舶的船框、船架和支撑结构,这些结构起到支撑和稳定船体的作用,使船舶能够承受水流、风力和重力等外部载荷。
此外,焊接结构还用于连接船舶的设备和机械部件,如发动机、推进器、舵机、锚链等。这些设备和机械部件需要与船体牢固地连接在一起,以确保船舶的正常运行和安全性。总之,焊接结构在船舶制造业中起着至关重要的作用,有助于增强船体的强度和刚度,使船舶能够承受各种外部载荷。
本文研究焊接结构件的疲劳失效特性,基于断裂力学和疲劳特性分析,研究船舶焊接结构件的焊接应力,并结合Ansys软件进行了焊接结构件的疲劳特性仿真。
1 船舶焊接结构件的疲劳失效特性通常,焊接结构件的疲劳失效可以分为以下几个阶段:
1)初始阶段
焊接结构件在使用过程中,由于受到外界因素的影响,如振动、冲击等,焊接结构件的某些部件可能会出现微小的损伤或变形。这些损伤可能不会立即导致焊接结构件的失效,但会逐渐积累并逐渐发展为更严重的问题。
2)加速阶段
在焊接结构件使用一段时间后,由于疲劳损伤的积累,焊接结构件的某些部件可能会出现更明显的疲劳失效现象,如裂纹、变形等。这些失效现象可能会导致焊接结构件的性能下降,甚至无法正常工作。
3)稳定阶段
焊接结构件在经过一段时间的使用后,疲劳失效的速度会逐渐减缓,并趋于稳定。焊接结构件的部件可能会出现更多的裂纹、变形等问题,但这些问题不会进一步加剧。
4)末期阶段
焊接结构件在经过长时间的使用后,疲劳失效的问题可能会变得更加严重。焊接结构件的部件可能会出现更多的裂纹、变形等问题,并且这些问题可能会进一步加剧,导致焊接结构件无法正常工作或完全失效。需要注意的是,不同的焊接结构件在不同的使用环境和使用条件下,疲劳失效的阶段和速度可能会有所不同。
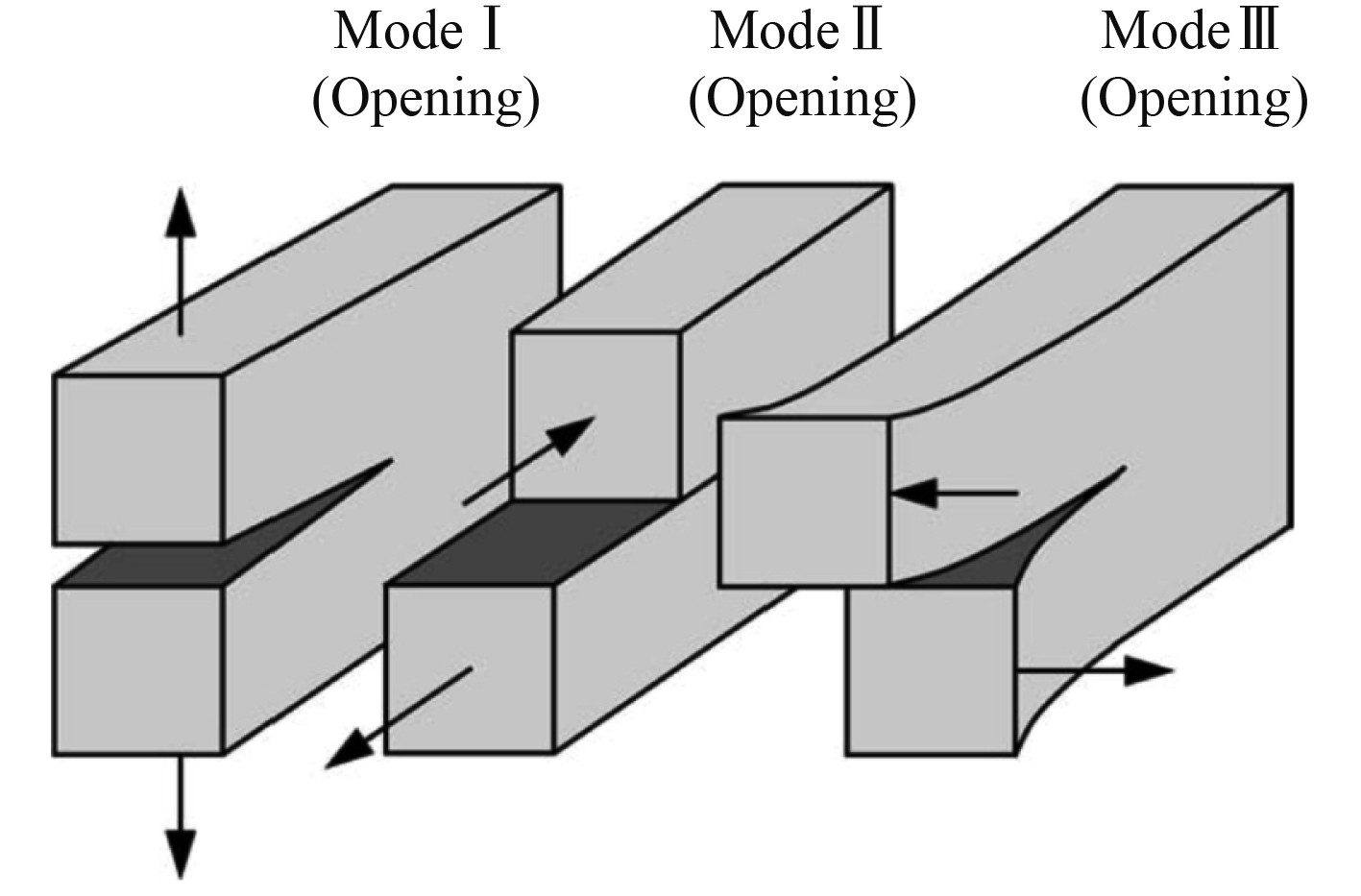
疲劳理论认为,结构件产生疲劳裂纹主要有图3种,分别是Modei-Mode III,如图1所示。
|
图 1 结构件焊接疲劳裂纹的种类示意图 Fig. 1 Schematic diagram of types of welding fatigue cracks in structural parts |
|
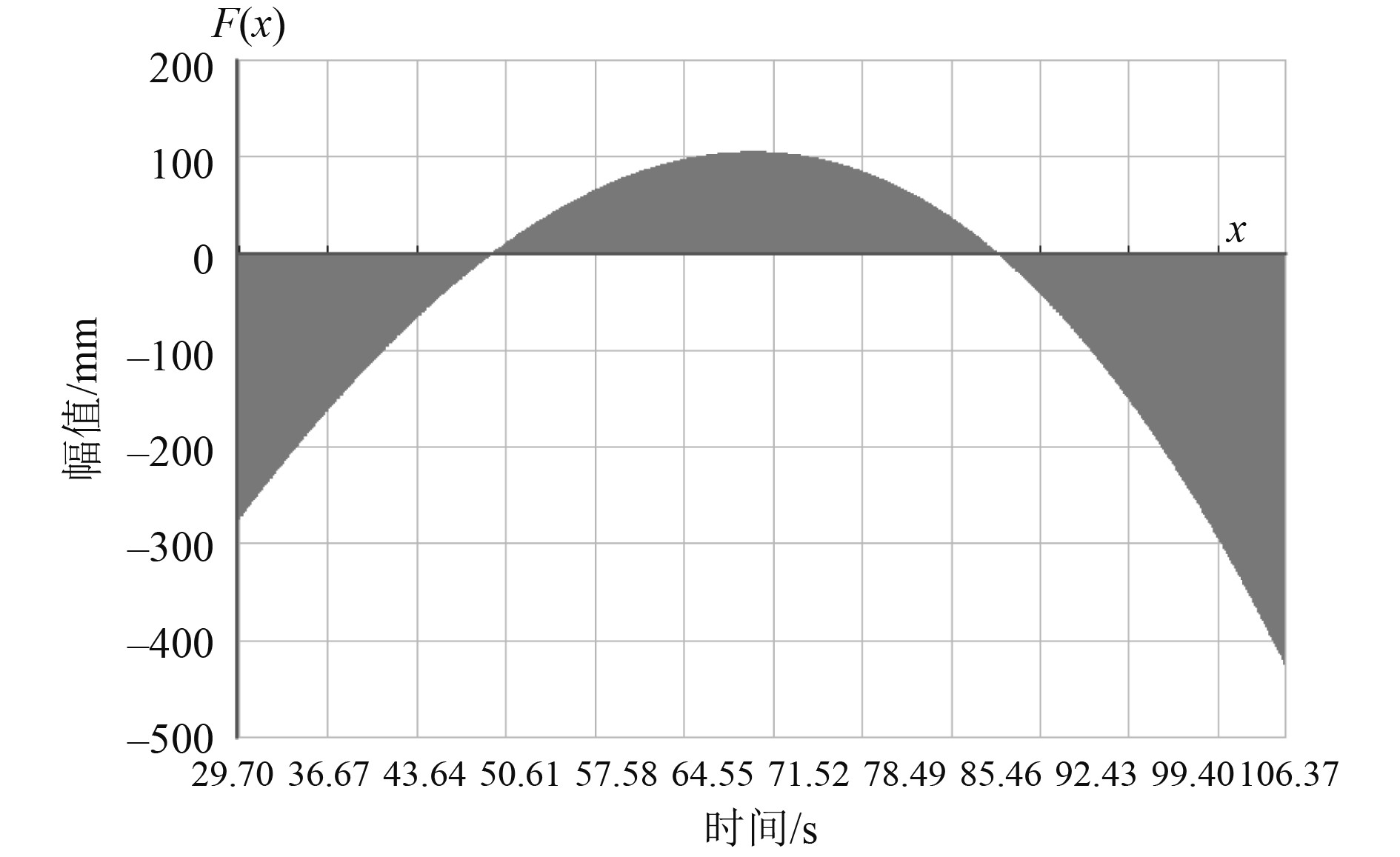
图 3 Longuet模型下的海浪波形示意图 Fig. 3 Wave waveform diagram under Longuet model |
在断裂力学中,应力强度因子K[1]可以表征裂纹附近应力场的强度,对于不同的焊接件疲劳裂纹形式,应力强度因子也不相同,用下式表示:
| $ \kappa = Y\sigma \sqrt {\text{π} a}。$ |
式中:
1)断裂力学的G准则
假定焊接结构件裂纹扩展的单位面积上释放的能量为G,G准则认为在一定时间内能量释放量G超过一个临界值后,结构件的裂纹就会发生失稳。可表示为:
| $ \begin{array}{l}G\geqslant {G}_{0},失稳,\\ G\leqslant {G}_{0}\text{,}稳定。\end{array} $ |
对于线弹性材料,当疲劳处于线弹性阶段时,应力强度因子与能量G准则可以相互转化:
| $ G = \frac{{{K^2}}}{{E'}} 。$ |
式中:
| $ E' = \frac{E}{{1 - {v^2}}} \text{,} $ |
此时,能量准则为:
| $ {G_{NC}} = \frac{{K'^2\left( {1 - {v^2}} \right)}}{E} 。$ |
2)断裂力学的COD准则
COD准则与结构的应变
| $ \begin{array}{l}\delta \geqslant {\delta }_{0},失稳,\\ \delta \leqslant {\delta }_{0}\text{,}稳定。\end{array} $ |
在平面应力场景下,材料的应变用下式计算:
| $ \delta = \frac{{8{\sigma _0}a}}{{\text{π} E}}\ln \sec \left( {\frac{{\text{π} \sigma }}{{2{\sigma _x}}}} \right) 。$ |
其中:
裂纹深度尺寸与材料的应力关系可用图2表示。可以看出,随着裂纹深度的增加,应力逐渐增加,超过一定临界值,材料发生屈服,应力不再增加。

|
图 2 裂纹深度尺寸与材料的应力关系曲线 Fig. 2 The relationship between crack depth size and stress of the material |
船舶舱室焊接结构在工作过程中受到的疲劳载荷有多种,包括海浪载荷和船舶运动载荷等。
本文选用的海浪扰动模型为Longuet模型[2],该模型下的海浪波形函数为:
| $ \xi \left( t \right) = \sum\limits_{i = 1}^n {\xi \cos \left( {k\psi \pm \omega t + {\varepsilon _i}} \right)} 。$ |
式中:
初始幅值
| $ {\xi _0}\left( t \right) = \sum\limits_{i = 1}^n {\xi \cos \left( {\omega t + {\varepsilon _i}} \right)} 。$ |
Longuet模型下的海浪波形示意图3所示。
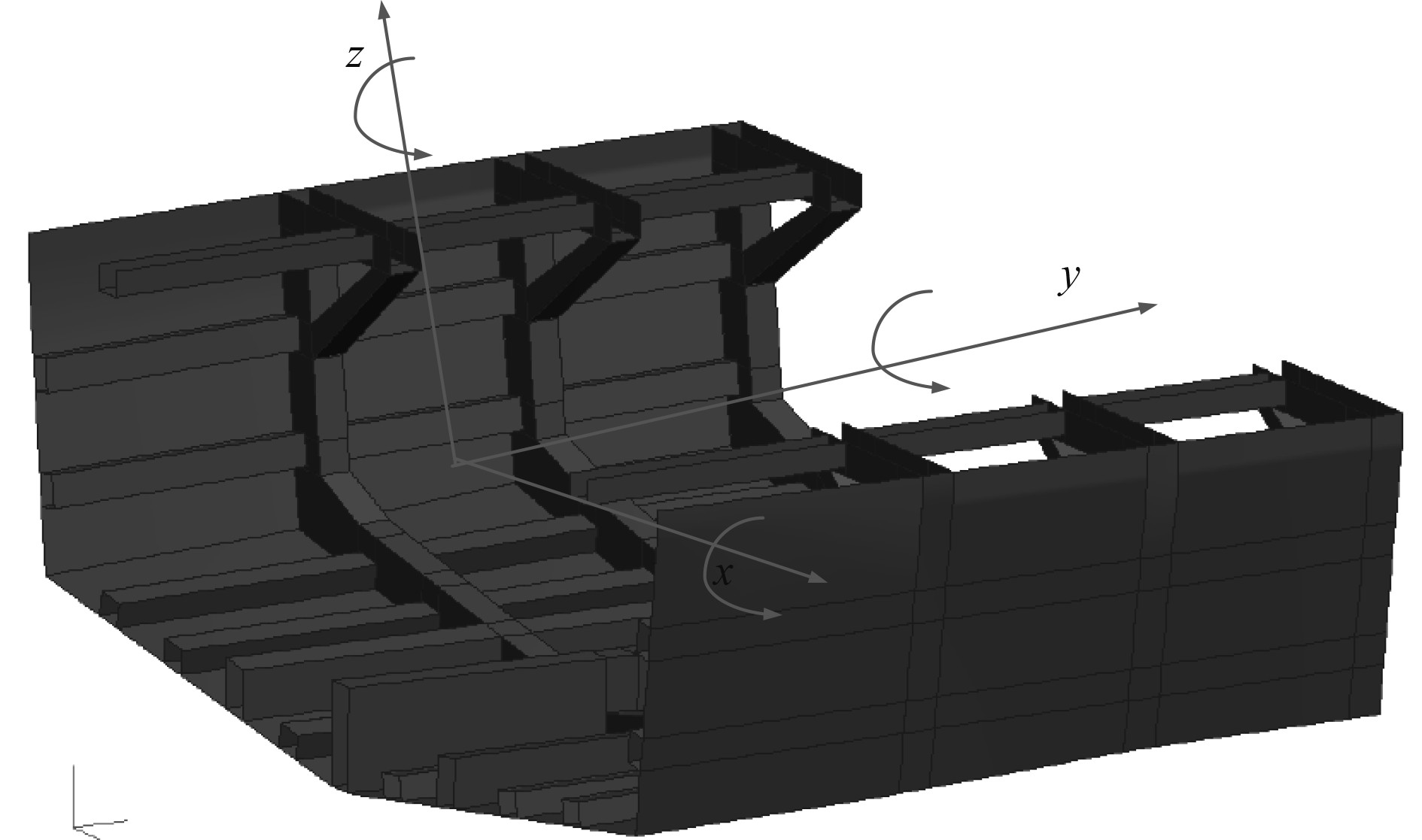
建立船舱结构的载荷坐标系如图4所示。
|
图 4 船舱结构的载荷坐标系 Fig. 4 Load coordinate system of cabin structure |
图中,以船舱结构的质心为原点,共有6个自由度,包括xyz3个坐标轴和绕3个坐标轴的旋转方向。
基于该坐标系,可以建立Longuet模型下的横摇倾角函数如下:
| $ {a_i}(t) = {\delta _T}\sum\limits_{i = 1}^n {{a_{\max }}\cos (\omega t + {\varepsilon _i})} 。$ |
式中:
船舶的纵摇周期按下式计算:
| $ {T_r} = 1.80\sqrt {\frac{L}{{10}}} \text{,} $ |
式中,L为船长。
最大纵摇角度按下式计算:
| $ {\varphi _{\max }} = 0.25\frac{{{\varphi _0}}}{{{C_b}}}。$ |
式中:
船舶结构件焊接时,由于高温热源的作用,焊接件会发生热膨胀和冷却收缩,从而产生应力。这些应力可能会导致焊接件的变形、裂纹和失稳等问题。焊接应力的大小受多种因素影响,包括焊接材料的热膨胀系数、焊接件的几何形状和尺寸、焊接过程中的温度梯度等。一般来说,焊接应力会集中在焊缝附近,尤其是焊接件的边缘区域。
建立船舶刚性结构的塑性应变与温度分布如下式:
| $ t(d) = \frac{{0.3{Q_0}}}{{\rho {C_0}\dfrac{\text{π} }{3}{D^2}}} \text{。} $ |
式中:
建立焊接结构件的热应变为:
| $ \delta (d) = {k_0}T(d) = \dfrac{{{k_0}0.3{Q_0}}}{{\rho {C_0}\dfrac{\text{π} }{3}{D^2}}} \text{,} $ |
式中,
进一步得到固有应变如下式:
| $ \eta (d) = {k_1}\delta (d) = \frac{{{k_0}{k_1}0.3{Q_0}}}{{\rho {C_0}{S_0}}}。$ |
式中:
图5对比了常压下和真空下热源距离与固有应变的影响关系。可见,以热源为对称中心,距离热源越远,结构的固有应变越小。

|
图 5 常压下和真空下热源距离与固有应变的影响关系 Fig. 5 Relationship between heat source distance and inherent strain under normal pressure and vacuum |
基于有限元分析软件Ansys进行船舶焊接结构的疲劳特性分析。
1)有限元建模
针对船舱焊接结构建立有限元模型,并根据结构的材料在Ansys中赋予材料属性,表1焊接结构的材料及属性表。
|
|
表 1 焊接结构的材料及属性表 Tab.1 Material and attribute list of welded structure |
2) 施加疲劳载荷谱
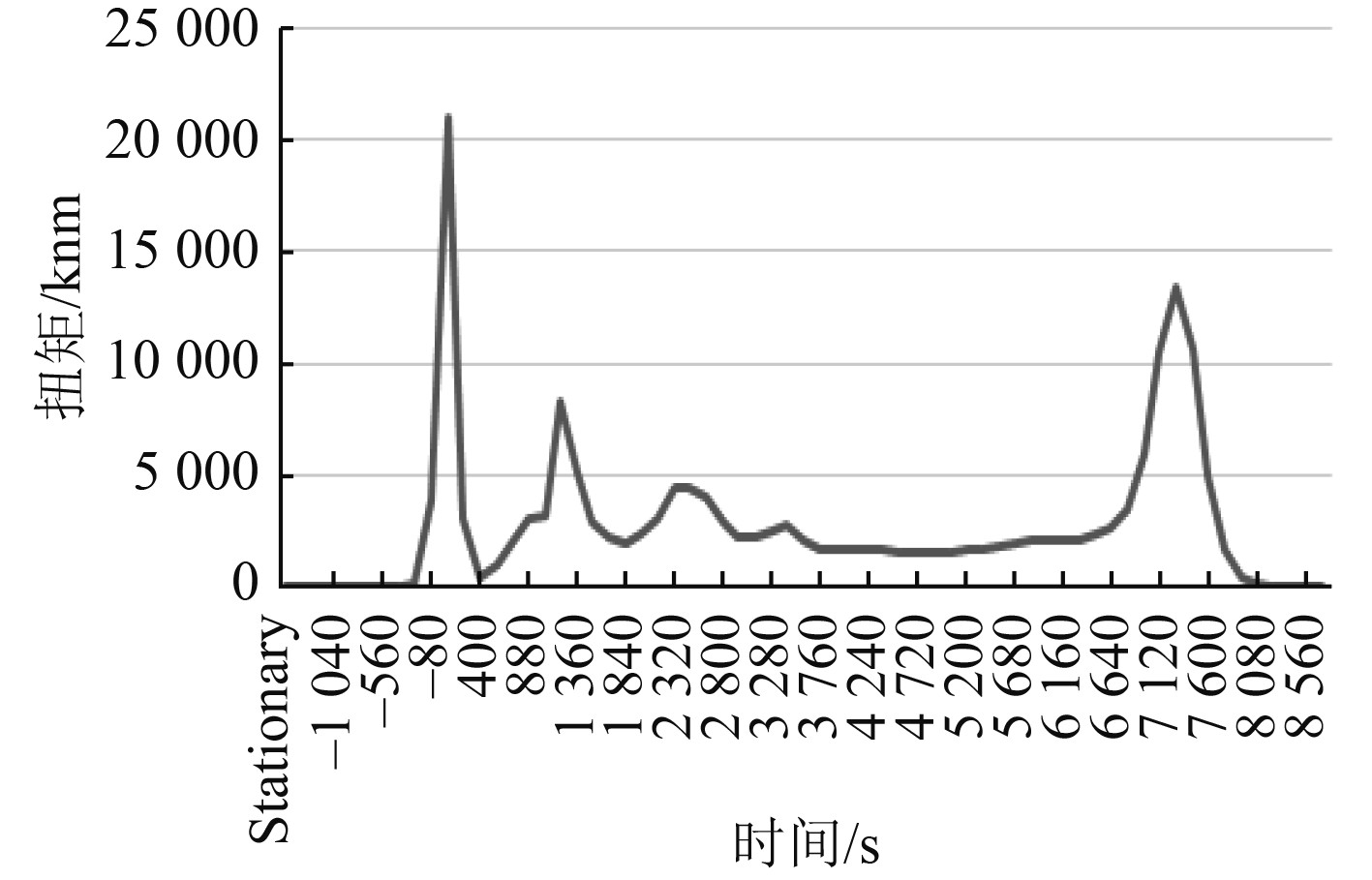
根据船舶焊接结构的实际工况,提取疲劳载荷谱如图6,载荷谱表征了时间与结构件受到扭矩的变化关系。
|
图 6 船舶焊接结构的疲劳载荷谱 Fig. 6 Fatigue load spectrum of welded structures of ships |
3)计算疲劳
焊接结构的损伤[4]用下式计算:
| $ {\text{D}} = \frac{{{v_0}{T_d}}}{{\bar a}}\sum\limits_{s = 1}^{{N_m}} {{p_n}} {q_n}\Gamma \left( {1 + \frac{m}{{{h_m}}}} \right) 。$ |
式中:
| $ {q_n} = \frac{{\Delta {\sigma _0}}}{{{{\left( {\ln {n_0}} \right)}^{1/h}}}}{,}\;{v_0} = \frac{1}{{4 \cdot {{\log }_n}(L)}} 。$ |
式中,
4)求解和结构优化
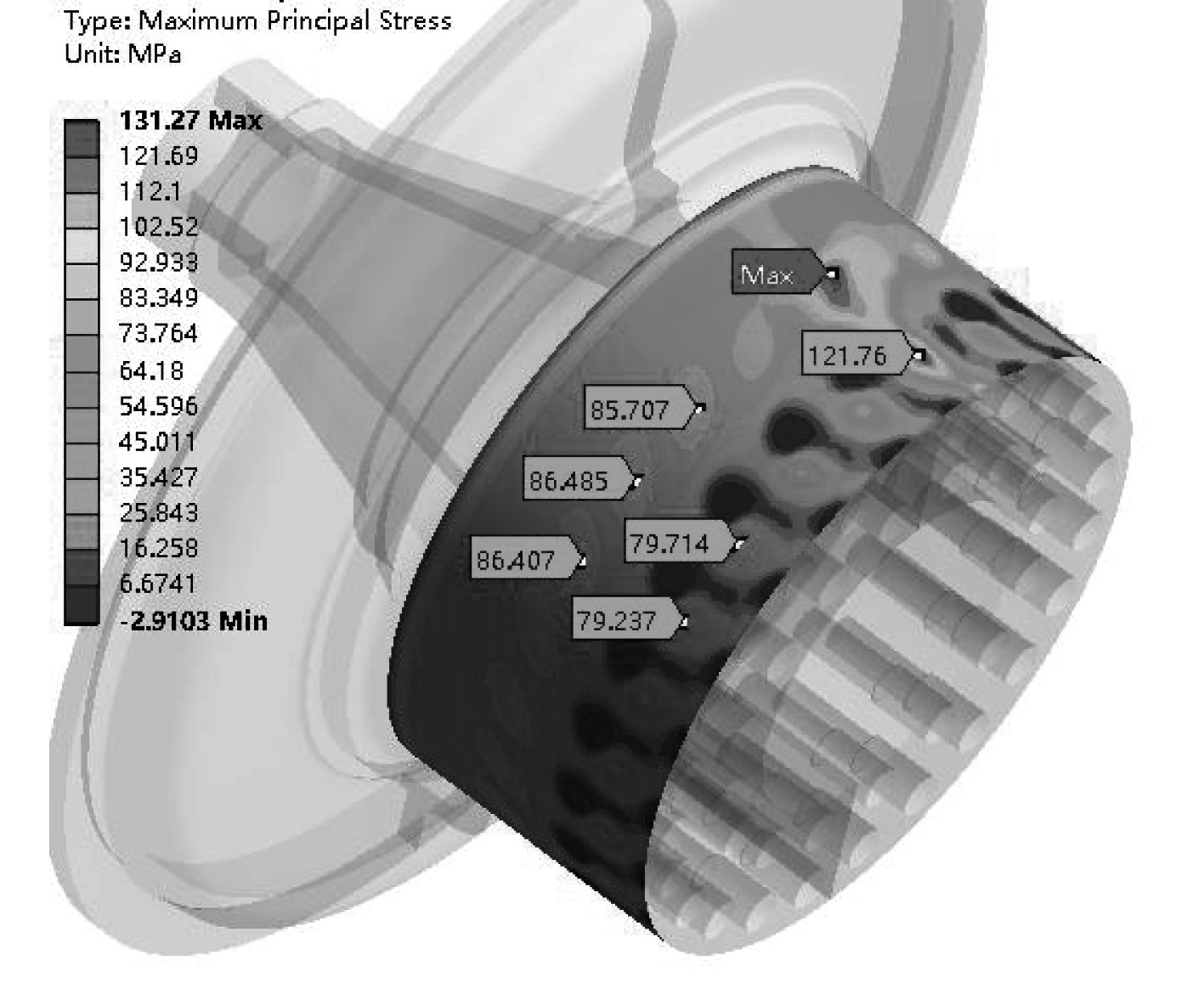
在Ansys中进行有限元求解,得到焊接疲劳载荷下应力最大的区域。图7为焊接区域疲劳载荷的仿真云图,可见最大应力为131.27 MPa。
|
图 7 焊接区域疲劳载荷的仿真云图 Fig. 7 Simulation cloud image of fatigue load in welding area |
为了提高船舶焊接件的结构强度和使用寿命,本文基于结构的疲劳特性与断裂力学理论,建立了船舱焊接结构的受力模型。采用Ansys进行了结构的疲劳特性仿真,有助于进行焊接结构的优化。
| [1] |
骆波, 邵力, 张洵浩, 等. T型单边焊接接头弯曲疲劳裂纹位置研究[J]. 农业装备与车辆工程, 2021, 59(3): 21-24. LUO Bo, SHAO Li, ZHANG Xun-hao, et al. Study on bending fatigue crack location of T-type unilateral welded joint[J]. Agricultural Equipment and Vehicle Engineering, 2021, 59(3): 21-24. |
| [2] |
杜丹阳, 任万滨. 基于原位拉伸台的焊接结构件疲劳试验研究[J]. 电工材料, 2019(5): 14-17. DU Dan-yang, REN Wan-bin. Fatigue test study of welded structural parts based on in-situ tensile table[J]. Electrical Materials, 2019(5): 14-17. DOI:10.16786/j.cnki.1671-8887.eem.2019.05.004 |
| [3] |
马园园, 谢里阳. 铝合金焊接结构件的断口分析[J]. 热加工工艺, 2018, 47(23): 250-253. MA Yuan-yuan, XIE Li-yang. Fracture analysis of aluminum alloy welded structural parts[J]. Hot Working Technology, 2018, 47(23): 250-253. DOI:10.14158/j.cnki.1001-3814.2018.23.063 |
| [4] |
冯继军. 焊接结构件的疲劳分析[J]. 焊接技术, 2017, 46(6): 78-80. FENG Ji-jun. Fatigue analysis of welded structural parts[J]. Welding Technology, 2017, 46(6): 78-80. DOI:10.13846/j.cnki.cn12-1070/tg.2017.06.022 |
 2023, Vol. 45
2023, Vol. 45
