随着现代电子战电磁环境越来越复杂,宽带数字信道化接收机以其宽处理带宽、高灵敏度、大动态范围、同时多信号处理能力等特点受到学者们的广泛关注。短时傅里叶变换(STFT)和多相滤波是常见的数字信道化实现工具[1-3],其中STFT相对算法简单,计算量小,消耗的硬件资源更少。考虑对低截获概率信号的侦收,子信道带宽不能太窄,信道数不能盲目增加,为了进一步提高检测灵敏度,对于子信道数据,采用自相关累加检测,能够以较小的计算量换取较大的灵敏度提升,实时性好,易于工程实现,因此大量学者对自相关检测和其参数测量展开研究[4-6],而频率作为信号分析的一项基本参数,提高其测量精度具有重要意义。王国华等[7]研究了信道化接收机瞬时自相关测频法,选取合适的相关延迟点,就可以通过瞬时自相关函数的相位获得信号的无模糊频率。周成群[8]研究了在STFT数字信道化接收机中,瞬时自相关测频改进算法。该算法利用多条延迟线提高测频精度,但是增加了多组乘法计算。
对于存在数据重叠的滑动STFT接收机,为了得到子信道自相关函数的无模糊相位,一般采用单点延迟自相关。由于滑动过程存在数据重叠,同一子信道相邻两个时刻噪声数据存在相关性,将导致自相关相位估计不准,从而导致测频误差,针对这种情况的相关研究较少。本文研究数据重叠STFT的子信道自相关函数,基于噪声部分的自相关均值不为0,提出一种相位校正方法,利用噪声功率校正相位,从而降低测频误差。
1 自相关测频假设带噪声的单频信号等间隔时间采样可以表示为:
| $ s(i) = A{e^{j2 \text{π} fi/{f_s}}} + n(i) 。$ | (1) |
其中:
| $ \begin{split} {R_{ss}} = &\frac{1}{L}\sum\limits_{i = 0}^{L - 1} {s(i + d){s^ * }(i)} = \\ & {A^2}{e^{j2 \text{π} fd/{f_s}}} + \frac{1}{L}\sum\limits_{i = 0}^{L - 1} {{e^{j2 \text{π} f(i + d)/{f_s}}}{n^ * }(i)} + \\ &\frac{1}{L}\sum\limits_{i = 0}^{L - 1} {{e^{ - j2 \text{π} fi/{f_s}}}n(i + d)} + \frac{1}{L}\sum\limits_{i = 0}^{L - 1} {n(i + d){n^ * }(i)} 。\end{split} $ | (2) |
其中:
记
| $ {\phi _{xx}} = 2\pi fd/{f_s} \approx \arctan \Bigg(\frac{{imag({R_{ss}})}}{{real({R_{ss}})}}\Bigg)。$ | (3) |
显然,可以通过式(3)计算信号频率。
对于延迟点数
| $ \left| {\frac{{2\text{π} fd}}{{{f_s}}}} \right| \leqslant \frac{\text{π} }{2}。$ | (4) |
对于时间序列s(0), ···, s(q), ···, s(q+1), ···, s(q+N), ···,其标准N点STFT为:
| $ {S^m}(q) = \sum\limits_{i = 0}^{N - 1} {s(i + q)w(i){e^{ - j2 \text{π} (i + q)m/N}}} 。$ | (5) |
其中:
时间序列滑动
| $ {S^m}(q + D) = \sum\limits_{i = 0}^{N - 1} {s(i + D + q)w(i){e^{ - j2 \text{π} (i + D + q)m/N}}} 。$ | (6) |
时间序列滑动
STFT数据重叠率对接收机的时间分辨率、最小脉冲处理能力及运算速度都有影响[9],综合考虑以上因素,一般选择50%的数据重叠率,即
将式(1)代入式(5)和式(6),滑动
| $\begin{split} & R_{ss}^m = \frac{1}{L}\sum\limits_{q = 0}^{L - 1} {{S^m}(q + \frac{N}{2}){{({S^m}(q))}^ * }} = \\ & \qquad \;{\kern 1pt} {A^2}{e^{jN \text{π} (\frac{f}{{{f_s}}} - \frac{m}{N})}}{\left| {\sum\limits_{i = 0}^{N - 1} {w(i){e^{j\text{π} i(\frac{f}{{{f_s}}} - \frac{m}{N})}}} } \right|^2} +\\ & \quad \quad \frac{A}{L}\sum\limits_{q = 0}^{L - 1} \sum\limits_{i = 0}^{N - 1} {w(i){e^{ - j2\text{π} \frac{f}{{{f_s}}}(i + q)}}} {e^{j2\text{π} (i + q)m/N}}\\ & \sum\limits_{i = 0}^{N - 1} {n(i + \frac{N}{2} + q)} w(i){e^{ - j2\text{π} (i + \frac{N}{2} + q)m/N}} + \\ & \quad \quad \frac{A}{L}\sum\limits_{q = 0}^{L - 1} (\sum\limits_{i = 0}^{N - 1} {w(i){e^{j2\text{π} \frac{f}{{{f_s}}}(i + \frac{N}{2} + q)}}} {e^{ - j2\text{π} (i + \frac{N}{2} + q)m/N}}\\ & \sum\limits_{i = 0}^{N - 1} {{n^*}(i + q)} w(i){e^{j2\text{π} (i + q)m/N}}) +\\ & \quad \quad \frac{1}{L}\sum\limits_{q = 0}^{L - 1} (\sum\limits_{i = 0}^{N - 1} {n(i + \frac{N}{2} + q)} w(i){e^{j2\text{π} (i + \frac{N}{2} + q)m/N}}\\ & \sum\limits_{i = 0}^{N - 1} {{n^ * }(i + q)} w(i){e^{ - j2\text{π} (i + q)m/N}}) 。\end{split} $ | (7) |
按照传统的频率估计方法,仅考虑式(7)的第1部分(记为
| $ \hat \phi _{xx}^m = N \text{π} \Bigg(\frac{{\hat f}}{{{f_s}}} - \frac{m}{N}\Bigg) = \phi _{ss}^m 。$ | (8) |
信号与噪声相互独立,式(2)的中间两部分仍近似服从均值为0的正态分布,但式(7)中第4部分数据并非完全独立,其均值不为0。将式(7)第4部分记为
| $ E(R_{nn}^m) = E\{ {\left| {n(i)} \right|^2}\} \sum\limits_{i = 0}^{N/2 - 1} {w(i)w\Bigg(i + \frac{N}{2}\Bigg)}。$ | (9) |
其中:
| $ \hat \phi _{xx}^m = \arctan \Bigg(\frac{{Y_{xx}^m}}{{X_{xx}^m}}\Bigg) = \arctan \Bigg(\frac{{Y_{ss}^m}}{{X_{ss}^m - E(R_{nn}^m)}}\Bigg) 。$ | (10) |
对于单个子信道相关积累后的结果,按照式(10)对其实部进行校正后计算得到校正后的相位估计值
|
|
表 1 仿真信号参数 Tab.1 Signal parameters used in simulation |
校正前频率测量结果如图1所示,可以看出,均值误差接近3.1 MHz。
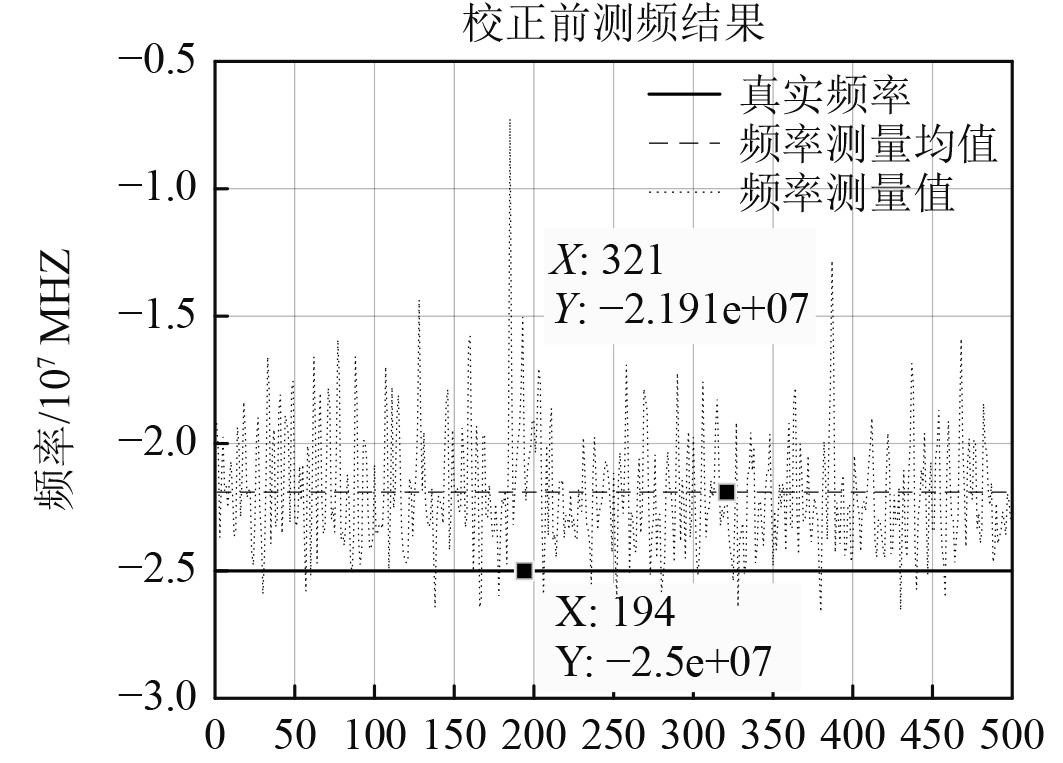
|
图 1 校正前测频结果示意图 Fig. 1 Diagram of frequency measurement results before correction |
由于窗函数为矩形窗,实部的校正量为
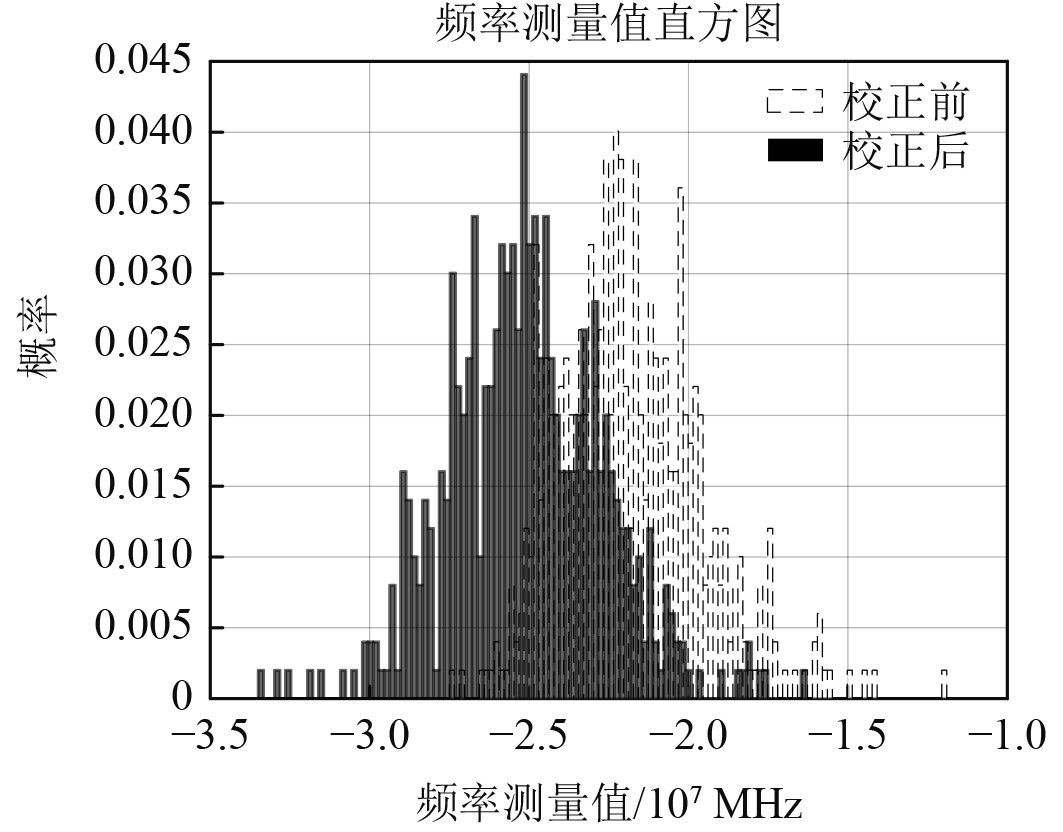
|
图 2 校正前后测频结果对比 Fig. 2 Comoarison of frequency measurement results before and after correction |
测频结果的均值误差及均方根误差对比见表2,可以看出校正后,均值误差和均方根误差均有减少。
|
|
表 2 校正前后频率测量均值误差及均方根误差 Tab.2 Mean error and rms error of frequency measurement before and affter correction |
按步进2dB逐步提高SNR,其余仿真条件不变,校正前后的均值误差如图3所示,均方根误差如图4所示。可见信号功率越低(即信噪比越低),校正效果越明显。

|
图 3 不同信号功率校正前后频率测量均值误差 Fig. 3 Mean error of frequency measurement before and after correction with different power |

|
图 4 不同信号功率校正前后均方根误差 Fig. 4 Rms error of frequency measurement before and after correction with different power |
将频率

|
图 5 不同频率校正前后均值误差 Fig. 5 Mean error of frequency measurement before and after correction with different frequency |

|
图 6 不同频率校正前后均方根误差对比 Fig. 6 Rms error of frequency measurement before and after correction with different frequency |
针对50%数据重叠的STFT信道化接收机,子信道单延迟自相关积累后,其相位受噪声数据相关性的影响,出现偏差,导致测频误差的问题,提出一种校正方法。该方法推导出部分重叠的噪声数据自相关后的均值,并且能够利用噪声功率对相位测量值进行校正,从而提高相位测量精度和频率测量精度,尤其在低信噪比情况下和子信道边界处,校正效果显著,仿真实验验证了该方法的有效性。对于单个子信道,仅增加了一次加法运算,计算复杂度很小,为以后工程化应用提供了一种可行性参考。
| [1] |
ZAHIRNIAK D R, SHARPIN D L, FIELDS T W. A hardware-efficient, multirate, digital channelized receiver architecture[J]. Transactions on Aerospace and Electronic Systems, 1998, 34(1): 137: 152.
|
| [2] |
LOPEZ-RISUENO G., GTAJAL J., SANZ-OSORIO A.. Digital channelized receiver based on time-frequency analysis for signal interception[J]. Transactions on Aerospace and Electronic Systems, 2005, 41(3): 879-898. DOI:10.1109/TAES.2005.1541437 |
| [3] |
龚仕仙, 魏玺章, 黎湘. 宽带数字信道化接收机综述[J]. 电子学报, 2013, 41(5): 949-959. GONG S X, WEI X Z, LI X. Review of wideband digital channelized receiver[J]. Acta Electronica Sinica, 2013, 41(5): 949-959. |
| [4] |
姚山峰, 曾安军, 严航, 等. 基于多重累积相关的LFM脉冲信号实时检测算法[J]. 电讯技术, 2011, 51(5): 71-76. YAO S F, ZENG A J , YAN H, et al. Real-time detection of LFM pulse signal based on cumulate-correlation[J]. Telecommunication Engineering, 2011, 51(5): 71-76. |
| [5] |
李全越, 武明西, 何航峰, 等. 基于自相关的脉冲信号检测方法[J]. 雷达与对抗, 2015, 35(3): 33–37. –LI Q Y, WU M X, HE H F, et al. An autocorrelation detection method for pulse signals[J]. Radar & Ecm, 2015, 35(3): 33–37. |
| [6] |
熊达福, 赵忠凯, 杨健. 基于数字信道化的弱信号检测方法研究与实现[J]. 火力与指挥控制, 2018, 43(12): 73-77. XIONG D F, ZHAO Z K, YANG J. Research and implementation for weak signal detection based on digital channelized[J]. Fire Control & Command Control, 2018, 43(12): 73-77. DOI:10.3969/j.issn.1002-0640.2018.12.015 |
| [7] |
王国华, 肖爽, 齐建文. 瞬时自相关信道化接收机频率测量研究[J]. 计测技术, 2006, 26(6): 10-12, 22. WANG G H, XIAO S, QI J W. Research of frequency measurement on instantaneous auto-correlation channelized IFM Receiver[J]. Metrology & Measurement Technology, 2006, 26(6): 10-12, 22. DOI:10.3969/j.issn.1674-5795.2006.06.003 |
| [8] |
周成群. 宽带数字信道化瞬时自相关测频技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [9] |
TSUI. J. 宽带数字接收机[M]北京: 电子工业出版社, 2002: 244–246
|
 2023, Vol. 45
2023, Vol. 45
