2. 大连大学 信息工程学院, 辽宁 大连116622;
3. 南京信息工程大学 电子与信息工程学院, 江苏 南京 210000
2. College of Information Engineering, Dalian University, Dalian 116600, China;
3. School of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210000, China
主动声呐系统具有海洋环境中目标信号检测、目标估计和定位、目标分类、识别和目标跟踪等功能[1],影响主动声呐探测性能的因素包括船舶噪声、海洋环境噪声,混响是主要因素。混响来自海水不均匀性引起的声散射,以及海面和海床的散射。目前,主动声呐信号处理中混响抑制是一个重要问题。
学者们提出了很多抗混响方法,主要包括基于AR预白化的去混响方法[2]、基于归一化匹配滤波的去混响方法[3]、基于主成分求逆算法(principal component inversion,PCI)的抗混响方法[4-5]以及基于低秩矩阵分解的抗混响方法[6-7]等。舒象兰等[2]在AR预白化的基础上,对接收信号进行二分法奇异值分解,以更好地抑制混响。但有一定的局限性,使用AR预白化方法时,确定AR系数的阶数非常困难。陈益明[3]提出了混合块归一化匹配滤波算法,减少了由于混响非平稳性所导致的标准块归一化匹配滤波输出虚峰。但该方法只能一定程度上减弱相关峰,并不能完全抑制。许策、刘贯凌等[4-5]利用PCI算法,根据混响和信号加背景噪声的功率差,将接收信号分为信号加背景噪声子空间和混响子空间,然后实现混响分离。但PCI方法很难估计秩,并且需要特定的先验知识。Wright等[6-7]利用低秩矩阵分解法将接收信号分为低秩矩阵和稀疏矩阵。低秩矩阵是混响子空间,稀疏矩阵是将接收信号与混响分离的信号子空间。但低秩矩阵分解法计算量较大,在某些实用性要求较高的场合并不适用。
稀疏表示的关键问题之一是过完备字典的设计,这在很大程度上决定了信号的特征能否被有效表示。字典有固定完整字典和学习字典2种类型[8]。固定完整字典主要通过一些数学函数变换,利用参数选择与信号相对应的原子,且要求原子数远大于信号长度。这种类型的常见形式包括离散小波变换(discrete wavelet transform,DWT)字典、离散余弦变换(discrete cosine transform , DCT)字典和Gabor字典。学习字典在固定词典的基础上添加了字典学习算法,并获得了第1类字典的最佳形式[9]。字典学习是稀疏表示的一个典型示例,其目的是识别从信号本身学习字典中一组信号的稀疏表示[10-11]。在迭代过程中,字典会根据给定的误差不断训练和更新原子,使其更接近信号的特征。与固定字典相比,使用训练字典可以降低算法的复杂度,更好地匹配信号的特征。
非负矩阵分解(non-negative matrix factorization, NMF) 是一种多变量子空间分析方法,自提出以来便得到深入研究和广泛应用[12]。其核心思想是在一定约束条件下将原始非负矩阵分解为2个低维的非负矩阵[13]。这种分解矩阵的非负性给这种描述数据的方式带来了一定的稀疏性。稀疏表示通过将主动声呐回波信号在所训练的字典上进行稀疏表示[14],使得信号具有一定稀疏性。因此,考虑将NMF应用到稀疏表示中,这样可以进一步提高主动声呐抗混响的性能。
本文介绍稀疏表示方法,提出一种基于稀疏表示的非负矩阵分解(non-negative matrix factorization, NMF)抗混响方法,并进行仿真模拟分析。
1 主动声呐回波信号模型用于水下主动声呐目标检测的声呐接收人造目标反射回波、海洋环境噪声和周围环境中目标随机散射形成的混响。将携带目标参数信息的目标反射回波从混响和噪声中分离出来是主动声呐检测的主要任务。
亮点模型是工程应用中水下目标散射回波形成机理的高频近似简化模型。该模型假设复杂目标由多个散射亮点组成,总目标回波是每个亮点产生的散射回波分量的线性叠加。亮点分为几何亮点和弹性亮点。几何亮点回波主要包括光滑表面上的镜面反射回波和角反射回波,这与物体大小、入射角有关。这种回波具有很强的能量,在实际目标检测中很容易观测到。弹性亮点回波是声波与介质界面相互作用的响应,取决于物体的材料特性和内部结构。考虑到这些回波的传播衰减较大,且回波能量通常较小,在混响信号(SRR)较低时难以观测。因此本文仅考虑几何亮点。
高光模型将目标视为一个线性系统,目标散射回波信号的表达式用传递函数表示。对于图1所示的目标结构,对应于目标的每个亮点显示的传递函数可以定义为:
|
图 1 目标结构示意图 Fig. 1 Schematic of the target structure |
| $ H(\omega ) = \sum\limits_{n = 1}^N {{A_n}(r,\omega ){e^{j\omega {\tau _n}}}{e^{j{\varphi _n}}}}。$ | (1) |
其中:
| $ x(t) = \sum\limits_{n = 1}^N {{x_n}(t)} = \sum\limits_{n = 1}^N {{A_n}s(t - {\tau _n}){e^{j{\varphi _n}}}} 。$ | (2) |
采用单元散射模型描述混响的形成机理。混响被模拟为入射声波散射回波的线性叠加,这是由于许多水下散射而产生的:
| $ R(t) = \sum\limits_{i = 1}^{N(t)} {K(t)s} (t - {\tau _i}){e^{j{\varphi _i}}}。$ | (3) |
其中:
| $ {\boldsymbol{x}}(t) = {\boldsymbol{As}}(t) + {\boldsymbol{n}}(t) = {{\boldsymbol{x}}_T}(t) + {\boldsymbol{r}}(t) + {\boldsymbol{n}}(t) 。$ | (4) |
其中,
正交匹配追踪(OMP)算法是一种基于稀疏分解理论的稀疏信号表示算法[15],由匹配追踪(MP)算法改进而来。匹配追踪算法是贪婪算法(greedy algorithm)的一种,其通过每次在过完备字典中选择一个与原始信号最匹配的最优原子[16],将这些最优原子进行线性组合,从而表示原始信号。
OMP算法过程如下:
输入:
输出:对
具体步骤如下:
步骤1 初始化残差
步骤2 通过计算残差
| $ {\lambda _t} = \arg {\max _{j = 1,...,d}}\left| {\left\langle {{r_{t - 1,}}\left. {{\varphi _j}} \right\rangle } \right.} \right| 。$ | (5) |
步骤3 更新所选原子的索引集
| $ {{\boldsymbol{\varPhi}} _t} = \left[ {{{\boldsymbol{\varPhi}} _{t - 1}}\left. {{\varphi _{{\lambda _t}}}} \right]}。\right. $ | (6) |
步骤4 更新稀疏矢量,由最小二乘法得:
| $ {\widehat s_t} = \arg {\min _x}{\left\| {v - {{\boldsymbol{\varPhi }}_t}\hat s} \right\|_2} 。$ | (7) |
步骤5 计算新残差:
| $ {r_t} = v - {{\boldsymbol{\varPhi}} _t}{\hat s_t} 。$ | (8) |
步骤6 判断是否满足
信号的稀疏度很大程度上由字典决定,因此字典的选择至关重要[17]。在进行稀疏表示时往往会先初始化一个字典,但它一般不是最优的。如固定的字典(DCT字典、Gabor字典等)对某些信号进行稀疏表示时效果很好,但不适用于其他信号。因此,有必要为特定的信号找到最合适的字典[18]。为此,将使用字典学习算法获取主动声呐回波信号在字典下的稀疏表示。
K-SVD算法2006年由Aharon[19]等提出。该算法推广了K-means聚类过程,通过在稀疏编码和更新字典原子之间交替执行训练超完备字典,以更好地表示数据。K-SVD算法过程为:
当给出训练集
| $ \mathop {\min }\limits_{D,X} \left\{ {\left\| {Y - DX} \right\|_F^2} \right\}{\text{ s}}{\text{.t }}\forall i,{\left\| {{x_i}} \right\|_0} \leqslant {T_0} 。$ | (9) |
其中
首先,设置具有
1)稀疏编码阶段
使用追踪算法计算每个示例
| $ X = \arg \mathop {\min }\limits_{{x_i}} \left\| {{y_i} - D{x_i}} \right\|_F^2{\text{ s}}{\text{.t }}\forall i,{\left\| {{x_i}} \right\|_0} \leqslant {T_0} 。$ | (10) |
2)字典更新阶段
通过求解一个小的奇异值分解(SVD)问题,一次只更新
| $ {{\boldsymbol{E}}_k} = Y - \sum\limits_{j \ne k} {{d_j}x_T^j} ,$ | (11) |
| $ {\boldsymbol{E}}_k^R = U\Delta {V^{\rm{T}}} 。$ | (12) |
其中:
由SVD算法步骤可以看出,该算法计算量小,可以刻画出数据的重要特征,因此实际应用范围很广。
3 基于NMF的协方差估计通过稀疏表示将主动声呐回波信号变换到稀疏域,改善信号的稀疏性。增加输出信号的稀疏性产生接近目标回波的信号,并根据这一特性,将其应用于去混响。
用NMF对稀疏表示信号
| $ {\boldsymbol{M}} \approx {\boldsymbol{WH}},{{ {\boldsymbol{W}}}} \in {\boldsymbol{R}}_{0 + }^{i \times k},H \in {\boldsymbol{R}}_{0 + }^{k \times j},$ | (13) |
协方差估计矩阵为:
| $ V = WH 。$ | (14) |
式中:
在NMF分解过程中,
以KL为代价函数优化NMF的问题可以总结如下:
| $ \min {D_{KL}}(M||WH) = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\left( {{M_{ij}}\ln \frac{{{M_{ij}}}}{{{{\left[ {WH} \right]}_{ij}}}} - {M_{ij}} + {{\left[ {WH} \right]}_{ij}}} \right)} } ,$ | (15) |
梯度下降算法为:
| $ \begin{gathered} {W_{ik}} = {W_{ik}} - {\mu _{ik}}\frac{{\partial {D_{KL}}(M||WH)}}{{\partial {W_{ik}}}},\\ {H_{kj}} = {H_{kj}} - {\eta _{kj}}\frac{{\partial {D_{KL}}(M||WH)}}{{\partial {H_{kj}}}} 。\\ \end{gathered} $ | (16) |
其中:
| $ \begin{gathered} \frac{{\partial {D_{KL}}(M||WH)}}{{\partial {W_{ik}}}} = - \sum\limits_{j = 1}^J {({H_{kj}}{M_{ij}}/{{[WH]}_{ij}} + {H_{kj}})},\\ \frac{{\partial {D_{KL}}(M||WH)}}{{\partial {H_{kj}}}} = - \sum\limits_{j = 1}^J {({W_{ik}}{M_{ij}}/{{[WH]}_{ij}} + {W_{ik}})} 。\\ \end{gathered} $ | (17) |
根据梯度下降算法,转化为乘法算法,令
| $ {\mu _{ik}} = \frac{1}{{\sum\limits_{j = 1}^J {{H_{kj}}} }},{\text{ }}{\eta _{kj}} = \frac{1}{{\sum\limits_{i = 1}^I {{W_{ik}}} }} ,$ | (18) |
将式(17)和式(18)分别代入式(16)中,则
| $ \begin{gathered} {W_{ik}} = {W_{ik}}\frac{{\sum\limits_{j = 1}^J {{H_{kj}}{M_{ik}}/{{[WH]}_{ik}}} }}{{\sum\limits_{j = 1}^J {{H_{kj}}} }},\\ {H_{kj}} = {H_{kj}}\frac{{\sum\limits_{i = 1}^I {{W_{ik}}{M_{ik}}/{{[WH]}_{ik}}} }}{{\sum\limits_{i = 1}^I {{W_{ik}}} }}。\\ \end{gathered} $ | (19) |
最后,将式(19)代入式(14),得到协方差估计矩阵
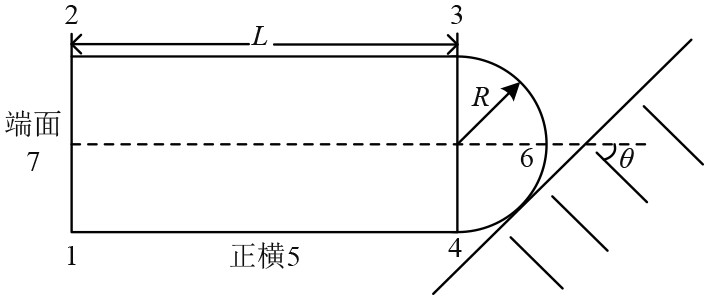
去混响算法流程如图2所示。首先对主动声呐回波信号进行稀疏表示得到稀疏信号
|
图 2 NMF去混响算法流程图 Fig. 2 Flow chart of NMF de-reverberation algorithm |
对基于稀疏表示的NMF去混响方法有效性进行仿真验证,发射信号为线性调频脉冲信号,频率范围为25~50 kHz,采样频率为500 kHz,发射信号脉宽为2 ms。
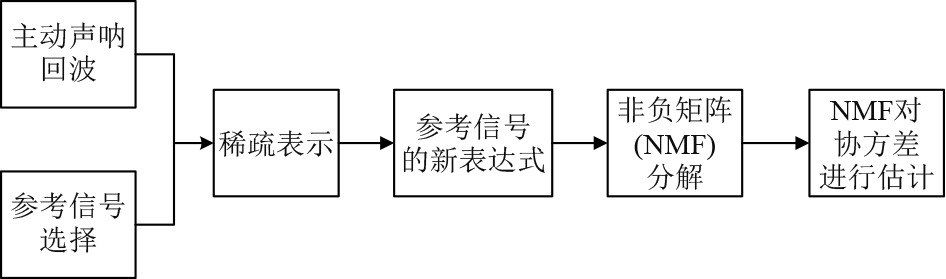
主动声呐目标回波仿真如图3所示。可以看出,对于主动声呐目标回波信号而言,对其进行稀疏表示是可行的,稀疏表示结果已经包含回波信号的大部分能量。因此,可以证明主动声呐回波可以进行稀疏表示,在混响背景下使用NMF抑制混响也具有可行性。
|
图 3 主动声呐回波信号 Fig. 3 Active sonar echo signal |
定义稀疏表示的相对均方误差为:
| $ {{error}} = \frac{{\left\| {s - \mathop s\limits^ \wedge } \right\|_2^2}}{{\left\| s \right\|_2^2}}。$ | (20) |
其中:
|
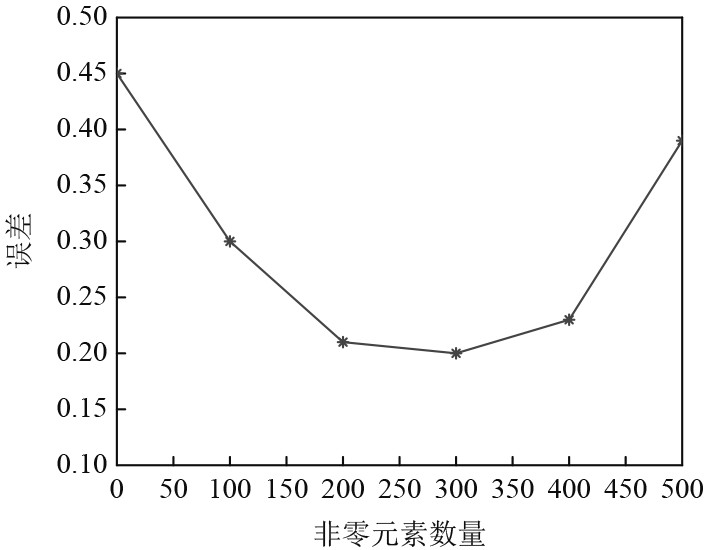
图 4 非零元素个数对误差的影响 Fig. 4 The effect of the number of non-zero elements on the error |
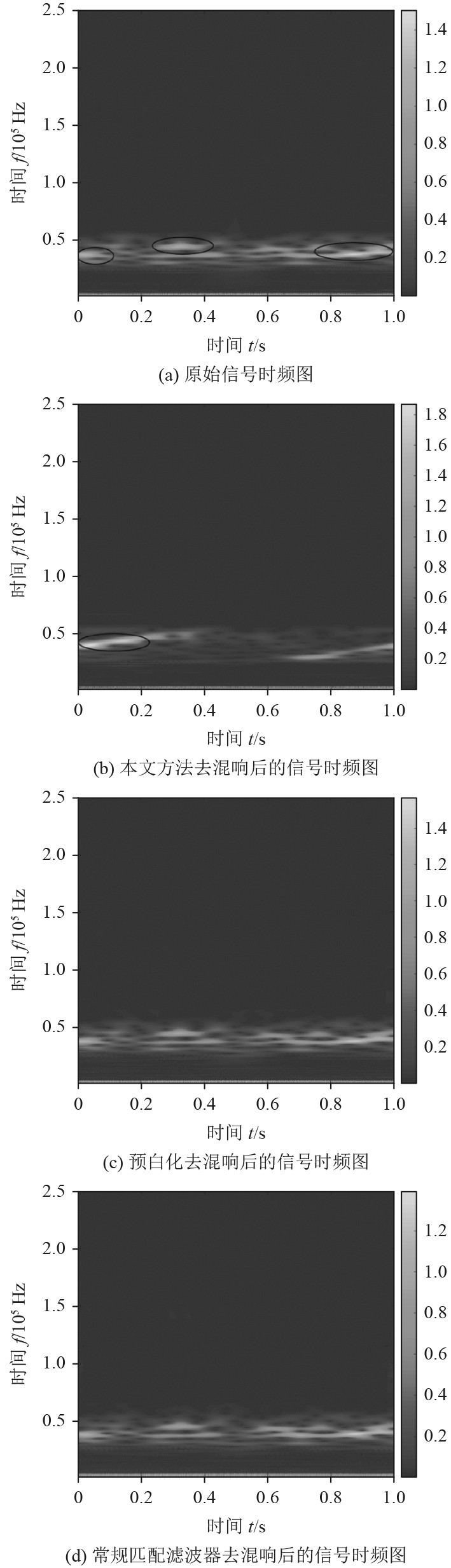
图5为原始信号以及采用预白化、常规匹配滤波和本文新方法对含混响的主动声呐回波信号进行处理后的时频图。
|
图 5 时频分布 Fig. 5 time-frequency distribution |
由图5(a)可以看出,亮斑1、亮斑2和亮斑3分别为目标亮点以及混响。由图5(b)可以清楚看到,经本文方法处理后,亮斑1即目标回波实现了增强,而混响2和混响3均被抑制。图5(c)和图5(d)分别为AR预白化、常规匹配滤波去混响后的信号时频分布,对比图5(b)可以明显看出,这2种方法虽去除了部分混响,但去混响效果远没有本文方法处理效果好。结果表明,该算法能有效抑制混响,提取目标回波成分。
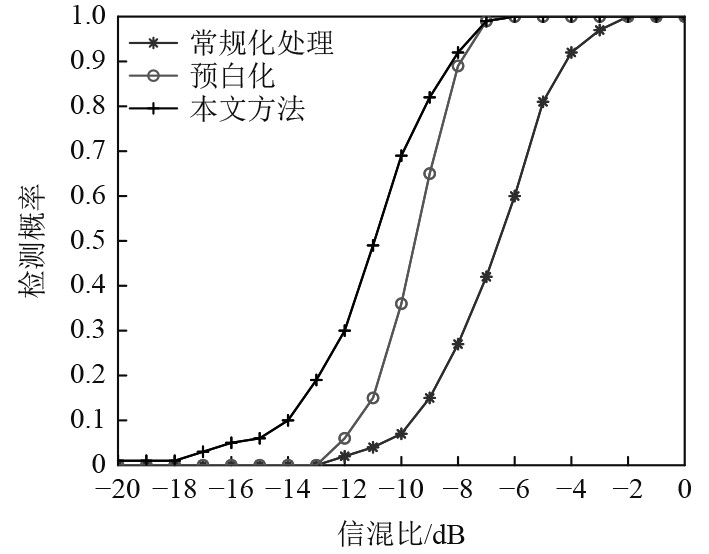
进一步分析3种去混响方法,通过1000次的蒙特卡罗实验,在虚警概率不大于0.1的前提条件下,得到的性能比较结果如图6所示。
|
图 6 3种检测信号方法的性能比较 Fig. 6 Performance comparison of three detection signal methods |
可知,本文方法优于其他2种方法。
5 结 语针对主动声呐抗混响问题,本文提出基于稀疏表示的NMF抗混响方法。充分考虑稀疏信号的稀疏性以及NMF的特性,计算声呐接收的目标回波信号的协方差,即以KL为代价函数,构造一个NMF优化问题,利用梯度下降法算法估计协方差,得到了协方差矩阵的估计值,进一步提高主动声呐目标回波去混响性能。实验结果表明,相对于其他去混响算法,本文提出的基于稀疏表示的NMF去混响方法,在一定程度上提高了主动声呐去混响性能。
| [1] |
李玉强, 徐燕, 周胜增. 海洋混响特性分析与建模仿真研究[J]. 舰船电子工程, 2018, 38(11): 86-88+182. DOI:10.3969/j.issn.1672-9730.2018.11.022 |
| [2] |
SHU Xianglan, SUN Rongguang, MA Xin. Echo detection of LFM signal under strong reverberation background[J]. Telecommunication engineering., 2016, 56(1): 82-87. |
| [3] |
陈益明. 混响背景下混合块归一化匹配滤波算法[C]//. 2013中国西部声学学术交流会论文集(下), 2013: 202-204.
|
| [4] |
许策, 章新华, 钱海民. 主动声呐中混响干扰的一种抑制方法[C]//. 2009年全国水声学学术交流暨水声学分会换届改选会议论文集. , 2009: 243-245.
|
| [5] |
刘贯领, 凌国民, 严琪. 主动声呐检测技术的回顾与展望[J]. 声学技术, 2007(2): 335-340. DOI:10.3969/j.issn.1000-3630.2007.02.035 |
| [6] |
ZHU G, SONG Z, YIN J, et al. Extracting target highlight feature based on low-rank matrix recovery in reverberation background[J]. Acta Acustica, 2019, 4: 471-479. |
| [7] |
WRIGHT J, GANESH A, RAO S, et al. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization[J]. Advances in neural information processing systems, 2009, 22. |
| [8] |
QAYYUM A, MALIK A S, SAAD M N M, et al. Evaluation of overcomplete dictionaries for image inpainting[J]. Science International, 2016, 28(4).
|
| [9] |
LI Junlin, WANG Huaqing, SONG Liuyang, et al. A novel feature extraction method for roller bearing using sparse decomposition based on self-Adaptive complete dictionary[J]. Measurement, 2019, 148(C).
|
| [10] |
VESHKI F G, VOROBYOV S A, A fast dictionary learning method for coupled feature space learning. [J]. CoRR, 2019, abs/1904.06968.
|
| [11] |
MA Xiaoyu, AHENG Jinsheng, LI Ting, et al. Super-Resolution geomagnetic reference map reconstruction based on dictionary learning and sparse representation[J]. IEEE Access, 2020, 8. |
| [12] |
何冲, 王冬霞, 王旭东, 等. 一种基于正交非负矩阵分解的多通道线性预测语音去混响方法[J]. 声学技术, 2018, 37(5): 468-474. DOI:10.16300/j.cnki.10003630.2018.05.011 |
| [13] |
高馨. 基于NMF的SAR图像目标识别方法研究[D]. 成都; 电子科技大学, 2013.
|
| [14] |
何天远. 基于信号稀疏表示的轴承故障诊断方法研究[D]. 石家庄: 石家庄铁道大学, 2020.000317.
|
| [15] |
李振, 李伟光, 陈辉, 等. 基于匹配追踪的特征频率提取算法及其应用[J]. 振动与冲击, 2019, 38(19): 7-13. DOI:10.13465/j.cnki.jvs.2019.19.002 |
| [16] |
王林. 非凸正则化稀疏表示方法及其旋转机械故障诊断应用研究[D]. 苏州: 苏州大学, 2019.
|
| [17] |
韩卫丽, 邹建成, 李建伟. 一种基于信号稀疏表示的语音去噪新方法[J]. 北方工业大学学报, 2013, 25(3): 6-11. DOI:10.3969/j.issn.1001-5477.2013.03.002 |
| [18] |
韩卫丽. 信号冗余表示理论在声音修复中的应用研究[D]. 北京: 北方工业大学, 2014.
|
| [19] |
MICHAL A, MICHEAL E, ALFRED B. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society, 2006, 54(11).
|
 2023, Vol. 45
2023, Vol. 45
