热力学仿真的基础就是通过引入熵概念,并将热通过对应的运动状态模型来表示。而麦克斯韦算法则主要研究了热分子运动与碰撞机制,对微观世界的粒子无序运动进行了系统的阐述[1-3]。到了20世纪末,伴随着机械化科学革命的蓬勃发展,热力学仿真中熵的概念逐渐流行。现如今,不少科研人员以这一科学概念为理论研究基础,将其与仿真软件进行结合,由此构建出了相关数学模型,并在实际应用研究中发挥着巨大作用[4-6]。本文以船舶增压锅炉为例,对其展开热力学仿真研究。并基于模糊自适应PID控制系统对其进行数学模拟,旨在拓展热力学的相关理论应用研究,在节约船舶增压锅炉能源,降低船舶运营成本的同时,提升船舶性能[7]。
1 热力仿真软件基础本文采用Matlab/Simulink软件环境对实际的热力模型进行仿真,为船舶增压锅炉的热力仿真构建一个良好的集成平台环境,通过设计出一套较为便捷的数学模型,方便在今后的热力学研究中构建出各种复杂的控制系统。同时,基于Matlab的Simulink工具对船舶增压锅炉进行热力学仿真研究,设计一个简单的界面来构建动态的仿真系统,提供一种更为方便、明确的建模方法,并通过模糊自适应PID控制系统实现数据的实时分析。
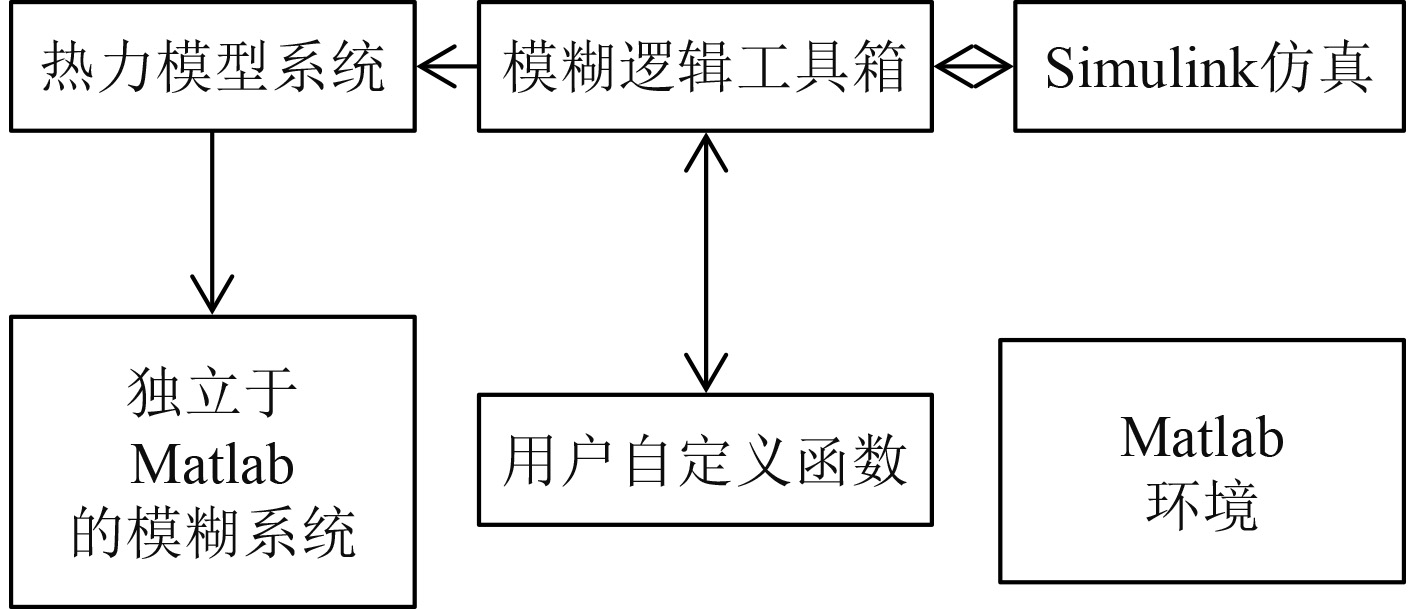
2 船舶锅炉热力仿真实验模型的建立 2.1 仿真环境的搭建在热力学仿真中结合模糊自适应PID算法,并按照如图1所示的流程搭建一个模糊自适应PID工具包,并通过Simulink工具进行数据的处理和分析。
|
图 1 模糊自适应PID逻辑工具箱及Simulink与Matlab的关系示意图 Fig. 1 Fuzzy adaptive PID logic toolbox and schematic diagram of the relationship between Simulink and Matlab |
首先建立稳定的热力学仿真环境,然后对船舶增压锅炉的燃油蒸汽参数进行控制,设定额定的进水温度为20°C,工作电压≥30 V,并将仿真模块分为前导区W01(s)和惰性区W02(s)。通过对过热器的出口处进行蒸汽温度测量,得出各部件的近似传递函数。
其中,前导区的传递函数为:
| $ {W_{01}}(s) = \frac{{{K_1}}}{{{{(1 + {T_1}s)}^{{n_1}}}}} \text{,} $ |
惰性区的传递函数为:
| $ {W_{02}}(s) = \frac{{{K_2}}}{{{{(1 + {T_2}s)}^{{n_2}}}}} 。$ |
从前导区和惰性区所含的时间常数和阶次等角度,可以依次得出各部件参数结果。
根据我国《船用辅助锅炉安全技术要求》(GB 31117–2014)相关要求规范,再结合以上各部件的参数结果,得出本研究中主回路调节器的PID参数为Kp=2,Ki=2/74,Kd=0。利用Matlab软件Simulink工具箱进行了模拟试验,建立船舶增压锅炉PID控制器。
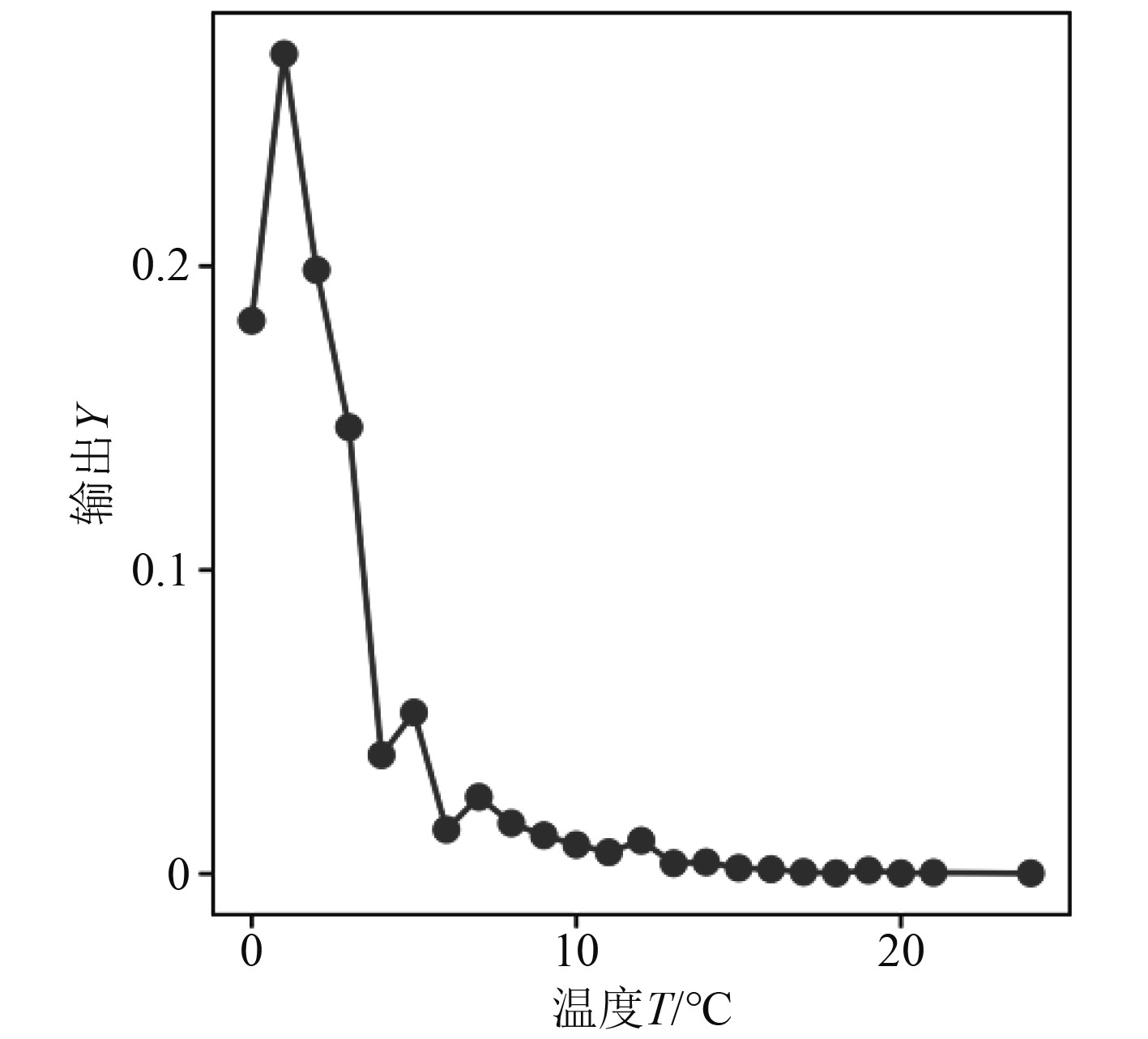
在常规PID控制系统中加入一个幅度为1的阶跃信号,得出锅炉主蒸汽温度传统PID控制输出曲线如图2所示。
|
图 2 锅炉主蒸汽温度传统PID控制输出曲线 Fig. 2 Output curve of traditional PID control for boiler main steam temperature |
可以看出,在温度为2℃时输出的PID控制参数达到最大值,然后随着温度的上升,输出量也会随之降低。常规PID的控制参数虽然可以满足船用锅炉的主蒸汽温度稳定要求,但在试验期间,其所需的调整时间比较长,因此在实际应用中并不理想。因此,采用模糊自适应PID控制算法对控制参数进行优化。
3 船舶增压锅炉热力学仿真模型构建 3.1 模糊自适应PID仿真模型船舶增压锅炉是一种比较复杂的传热装置,在工作原理上是按照一定的排列顺序进行热量传导,在控制系统中,过热器的控制目标一般分为前、后2个部分。在经过过热器时,工质会先流入过热器,在满足汽轮机工作要求的同时,对其出口蒸汽温度进行适当的调节,从而间接地控制其出口的温度。
需要注意的是,船用锅炉对应的系统在后续研究中将对其统一为混合控制模块。其中主回路要保证比例和积分的功能一致;外回路主要起到消除系统内部干扰的作用;副回路则是作为辅助配件,实现船舶增压锅炉最大限度的调节效果。
本文设置的PID控制器核心部分为参数相关的模糊自适应调节矩阵,通过该矩阵结合PID参数,实现了PID参数的模糊自适应调节矩阵,可以方便地进行PID参数的调节。
其中,核心矩阵参数的调整公式分别为:
| $ \begin{gathered} {K_p} = {{K'}_p} + \left\{ {E,EC} \right\}{K_p} = {{K'}_p} + \Delta {K_p},\\ {K_i} = {{K'}_i} + \left\{ {E,EC} \right\}{K_i} = {{K'}_{\text{i}}} + \Delta {K_i},\\ {K_d} = {{K'}_d} + \left\{ {E,EC} \right\}{K_d} = {{K'}_d} + \Delta {K_d}。\end{gathered} $ |
式中:Kp、Ki和Kd为PID控制参数;
从船用锅炉机组的工作情况来看,通过计算机测控系统可以不断地对系统的输出进行监测,并对误差的变化速率进行实时计算,对该偏差进行模糊处理。通过对模糊校正矩阵的查询,可以得到Kp、Ki和Kd三种参数的归一化结果。基于以上参数,通过对船用锅炉主蒸汽温度的模糊自适应PID控制器的参数进行优化,从模糊PID控制器的设计原理出发,建立相应的控制规则,由此得出了常规PID参数的调节规则,最终创建出了最优化的模拟系统。
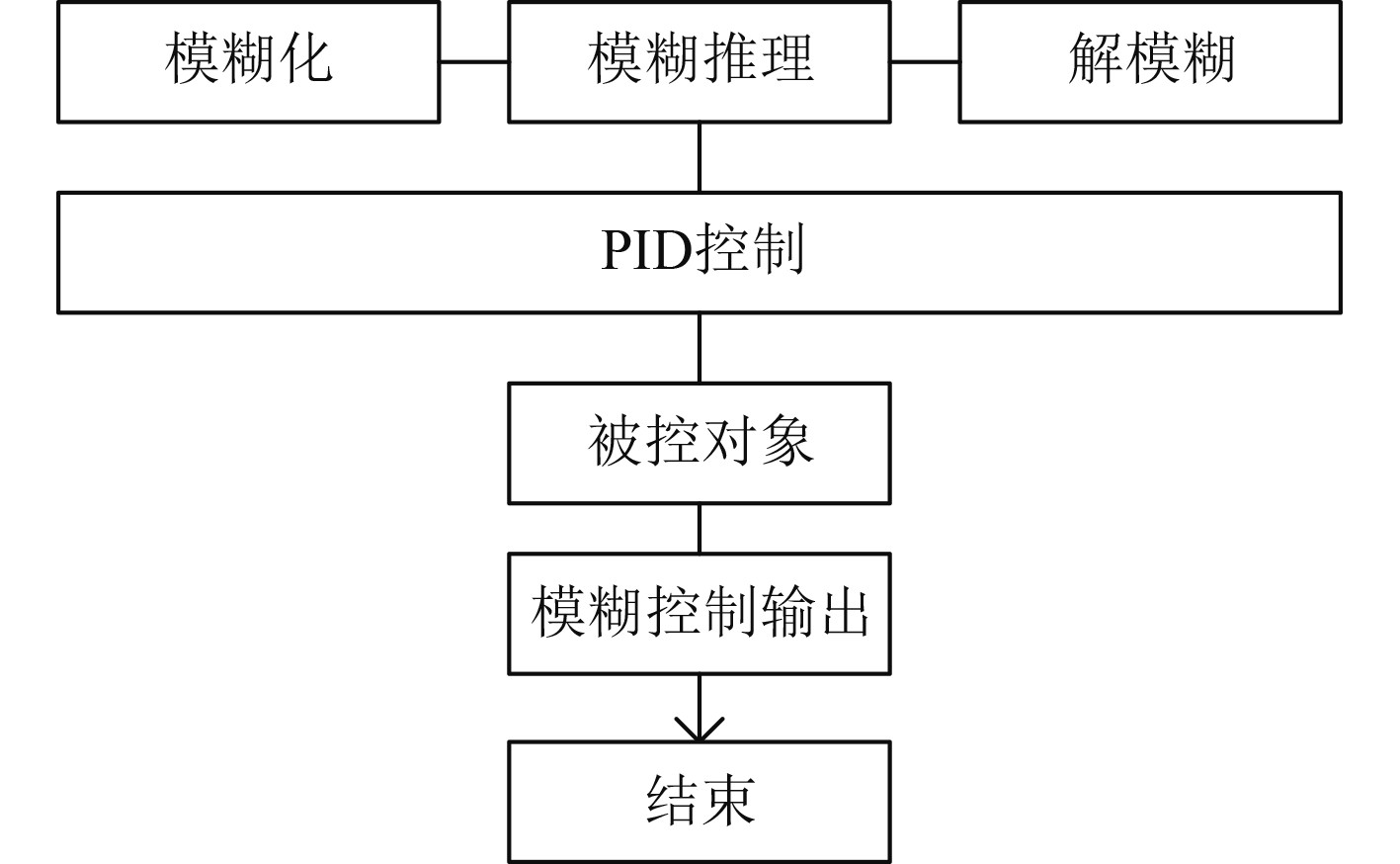
3.2 船用增压锅炉主蒸汽温度的仿真研究在实际应用中,锅炉内部煤粉的用量和空气的用量是成正比的。因此在考虑了供煤量对主汽温度的重要因素后,将模糊控制器和PID控制器有机地结合起来,通过对煤量阶跃变化的情况进行分析,构建了基于模糊PID的主蒸汽温度-给煤量优化系统,模糊自适应基础上的PID控制器主蒸汽温度-给煤优化系统示意图如图3所示。
|
图 3 模糊自适应基础上的PID控制器主蒸汽温度-给煤优化系统示意图 Fig. 3 Schematic diagram of PID controller main steam temperature coal feeding optimization systembased on fuzzy adaptive control |
模糊控制器和PID控制器在主蒸汽温度-给煤量系统中,作为内环控制器很好实现了相应的PID控制。假设内环供煤量控制器为二维的,则其输入为实测煤量与预设值的偏差e,计算该偏差的真实值。输入数据在经过模糊化等一系列处理后,最终得到3个输出PID控制器的参数,分别为:
| $ \begin{gathered} {K_{pf}} = {K_{p0}} + \Delta {K_p},\\ {K_{if}} = {K_{i0}} + \Delta {K_i},\\ {K_{df}} = {K_{d0}} + \Delta {K_d}。\\ \end{gathered}$ |
根据PID控制的基本原理,对船舶的增压锅炉进行热力学仿真进行控制。
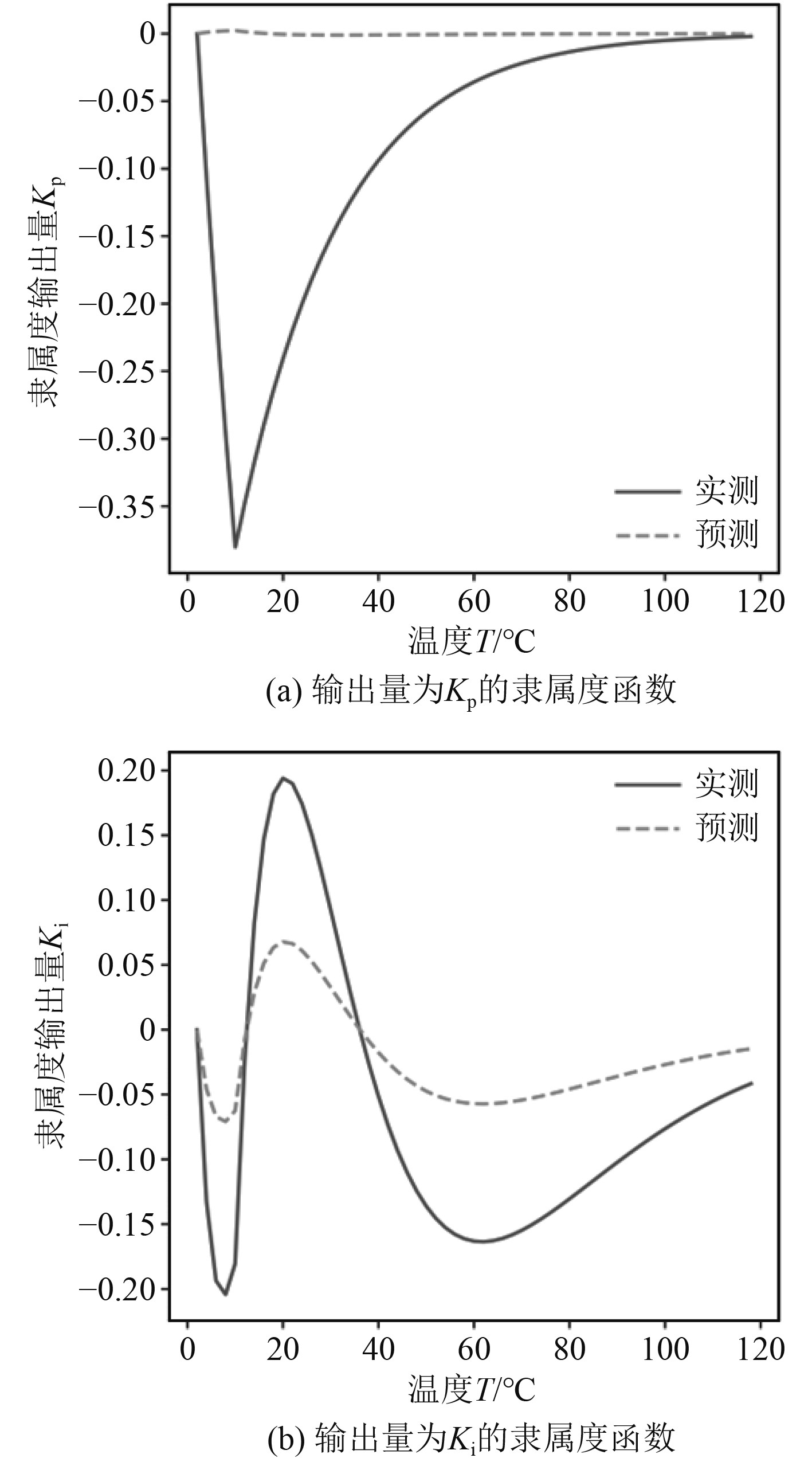
4 基于模糊自适应PID控制系统的船舶增压锅炉热力学模型设计 4.1 模糊自适应PID控制系统的结构设计为进一步论述热力学仿真控制系统的可行性,利用误差e和误差的真实变化率ec来获得输入状态变量,然后针对PID控制器中比较重要的Kp、Ki控制量进行优化。针对隶属度函数进行优化设计,得到如图4所示的相关隶属度函数图。可以看出,输出量分别为Kp和Ki的隶属度函数在温度100℃后开始稳定。
|
图 4 Kp和Ki的相关隶属度函数图 Fig. 4 Correlation membership function diagram of Kp and Ki |
模糊控制语言是由“if…then…”来表达的,在输入和输出之间用and关系来连接,参数为Kp、Ki、Kd,表1为 Kp的控制规则调整表。
|
|
表 1 Kp的控制规则调整表 Tab.1 Control rule adjustment table for Kp |
遵循If (e is NB) and ( ec is NB) then (pk is PB)(ik is NB)(dk is PS)原则,在PID模糊自适应控制系统中输入量为进煤量和设置值,这2个值会引起偏差e,得出PID控制系统的输出的3种不同变量。
为满足精确性的要求,需要对煤量偏差e和偏差改变量ec分别进行设定,将输入量的模糊划分区域按一定的规则进行划分。根据实际的船舶锅炉的运行情况,将锅炉的给煤量偏差e设定为[–10,10],而从偏离变动ec的基本论域来考虑,则设定为[–3,3]。
为了与输入量保持一致性,需要对输出量ΔKp、ΔKi、ΔKd的模糊划分数目进行确定,以字母来表示其模糊子集,并按顺序设定为{NB、NM、NS、ZE、PS、PM、PB}。从输出的数量上来看有13个级别,所以这个时候,输出量的模糊限定量可以被设定成固定值。根据PID三个不同的参数的实际变化情况,得出ΔKp的相关区域为[–5,5],ΔKi的相关区域为[–1,1],而ΔKd的相关区域为[–3,3]。
PID的控制参量可以分别进行量化和优化,所谓的量化是指对输入量进行数值化分析。通过它可以测量模糊输入量控制效果的程度,将偏离e和偏离改变ec对应的量化系数进行确定,参见下式:
| $ {K_e} = n/{x_e} \text{,} $ |
式中:xe为偏离e的基础论域的区间;n为偏离e的模糊论域的区间。量化后得出:
| $ {K_{ec}} = m/{x_{ec}} 。$ |
由以上Ke与Kec两式得出各对应的定量因数,如下式:
| $ {K_e} = 6/10 = 0.6 \text{,} $ |
| $ {K_{ec}} = 6/3 = 2 。$ |
通过对比例系数的分析,可以将输出数据的模糊性转化为更准确的数据。如果将系统输出量的模糊论域设定为[–1, 1],将基础论域设定为[–yu, yu],则输出量的标度系数见下式:
| $ {K_u} = \frac{{{y_u}}}{l} \text{,} $ |
根据Kup、Kui、Kud所计算的量化系数进行相应的调整,可以更好地描述模糊子集的从属关系。
一般而言,在模糊控制器的设计中需要特别注意输入参量的隶属度配置。根据其形态,通常将其划分为四大类:高斯隶属度、Z型隶属度、梯形隶属度、三角隶属度。考虑到控制的敏感性和稳定性,可以根据其实际工作区间的差异,采用三角隶属度和高斯隶属度函数,实现了多个区域的控制。三角隶属度函数的外形具有高度尖细的特点,适合于偏移比较少的区域。因此,在NM、NS、ZE、PS、PM等模糊子集中,利用三角隶属度函数可以保证控制的准确性,并且在NB和PB的模糊子集上,可以保证系统的稳定。由于锅炉装置进煤的数量造成的偏差e,其偏差随时间的变化而变化,因此输出量ΔKp、ΔKi、ΔKd的隶属关系也会随之自动变化。
5 结 语本文以船舶增压锅炉为例,从传统PID控制系统中的主要蒸汽温度出发,阐述了PID控制器的基本原理及相关的工程应用。同时,结合热力学仿真对模糊自适应PID控制进行了具体的数值模拟,提出了一种基于主蒸汽温度模糊自适应PID控制方案,并对其进行了仿真和比较。实验表明,与常规PID相比,模糊自适应PID控制器具有更好的控制性能。
| [1] |
吴文亚, 魏博, 李光辉, 等. 腐蚀气体与铁基化合物反应的热力学分析[J]. 新疆大学学报(自然科学版)(中英文), 2021, 38(2): 168-173. WU Wen-ya, WEI Bo, LI Guang-hui, et al. Thermodynamic analysis of the reaction between corrosive gases and iron-based compounds[J]. Journal of Xinjiang University (Natural Science Edition) (Chinese and English), 2021, 38(2): 168-173. |
| [2] |
李瑞华, 朱子琪, 王娜娜, 等. 燃煤锅炉烟气冷凝节水的热力学分析[J]. 锅炉技术, 2019, 50(6): 22. LI Rui-hua, ZHU Zi-qi, WANG Na-na, et al. Thermodynamic analysis of coal-fired boiler flue gas condensation water saving[J]. Boiler Technology, 2019, 50(6): 22. DOI:10.3969/j.issn.1672-4763.2019.06.005 |
| [3] |
陈翀, 林婵, 陈蒙, 等. 供热锅炉系统热力学分析[J]. 机电产品开发与创新, 2019, 32(2): 39-41. CHEN Chong, LIN Chan, CHEN Meng, et al. Thermodynamic analysis of heating boiler system[J]. Electromechanical Product Development and Innovation, 2019, 32(2): 39-41. DOI:10.3969/j.issn.1002-6673.2019.02.014 |
| [4] |
杨勇平, 黄圣伟, 徐钢, 等. 电站锅炉烟气余热利用系统的热力学分析和优化[J]. 华北电力大学学报(自然科学版), 2014, 41(1): 78-83. YANG Yong-ping, HUANG Sheng-wei, XU Gang, et al. Thermodynamic analysis and optimization of utility boiler flue gas waste heat utilization system[J]. Journal of North China Electric Power University (Natural Science Edition), 2014, 41(1): 78-83. |
| [5] |
黄圣伟, 徐钢, 杨勇平, 等. 电站锅炉烟气余热利用的热力学分析与优化设计原则[J]. 现代电力, 2013, 30(1): 75-80. DOI:10.3969/j.issn.1007-2322.2013.01.016 |
| [6] |
刘旭东, 盛伟, 关多娇, 等. 超临界600MW锅炉膜式水冷壁的热力学行为研究[J]. 热力发电, 2010, 39(11): 27. |
| [7] |
刘钊, 谢亚楠, 汪波. 汽车空调热力膨胀阀容量测试技术研究及应用[J]. 湖北大学学报(自然科学版), 2023, 45(4): 643-648. |
 2023, Vol. 45
2023, Vol. 45
