高速永磁电机因其高功率密度、高效率以及易于控制的特点,已广泛应用于航空航天、交通运输以及新能源发电等领域[1-3]。高功率密度的特点使得电机单元体积内的损耗较高,易产生较大温升,严重影响电机运行性能[4-5]。为了准确分析永磁电机的温升特性,电磁热耦合分析得到了广泛应用,相较于传统分析方法,耦合计算方法可有效提高电机温升的预测精度。
目前较为常用的电磁热耦合分析模型主要包括。有限元耦合模型和场-路耦合模型。有限元耦合指的是电磁场有限元模型与温度场有限元模型或者计算流体力学模型(CFD)之间的耦合,这种模型计算精度较高,且可获得电机温度场分布及热点位置[6]。VESE等[7]采用二维电磁场与三维温度场耦合的方法对永磁电机额定工况下的温度场进行分析,结果表明多物理场间的耦合分析结果可作为电机设计和性能优化的依据。JOO等[8]采用三维电磁场与三维温度场的耦合模型对永磁电机的瞬态温升特性进行了分析,并研究了轴向风冷对绕组绝缘温升和永磁体退磁的影响。但有限元耦合模型的计算速度较慢且建模复杂,不适用电机的初始设计阶段。场-路耦合指的是电磁场有限元模型与等效热网络模型间的耦合,等效热网络模型建模简单且计算效率较高。韩雪岩[9]采用场-路耦合的方法研究了水冷轴向磁通电机的温升特性,并且基于该模型分析了冷却液流速以及装配间隙对电机温升的影响,但是电磁计算采用时步有限元方法,耗时较长。LI等[10]基于场-路耦合模型分析了开关磁阻电机驱动周期内的瞬态温升特性,但是仅考虑了电磁场与温度场间的单向耦合。
针对现有场-路耦合模型的不足,本文基于二维静磁场有限元模型和等效热网络模型建立了一种高效的场-路耦合计算模型。首先,基于磁密时空变换公式,推导了永磁电机电磁损耗计算模型,并采用二维时步有限元分析进行验证;然后,基于传热学定律建立了电机的等效热网络温度场分析模型,并推导了节点稳态和瞬态温升计算的状态空间方程。最后,以一台4极48槽永磁同步电机为例,采用三维有限元耦合模型与场-路耦合模型进行对比,证明本文所建立的电磁热耦合模型的有效性。
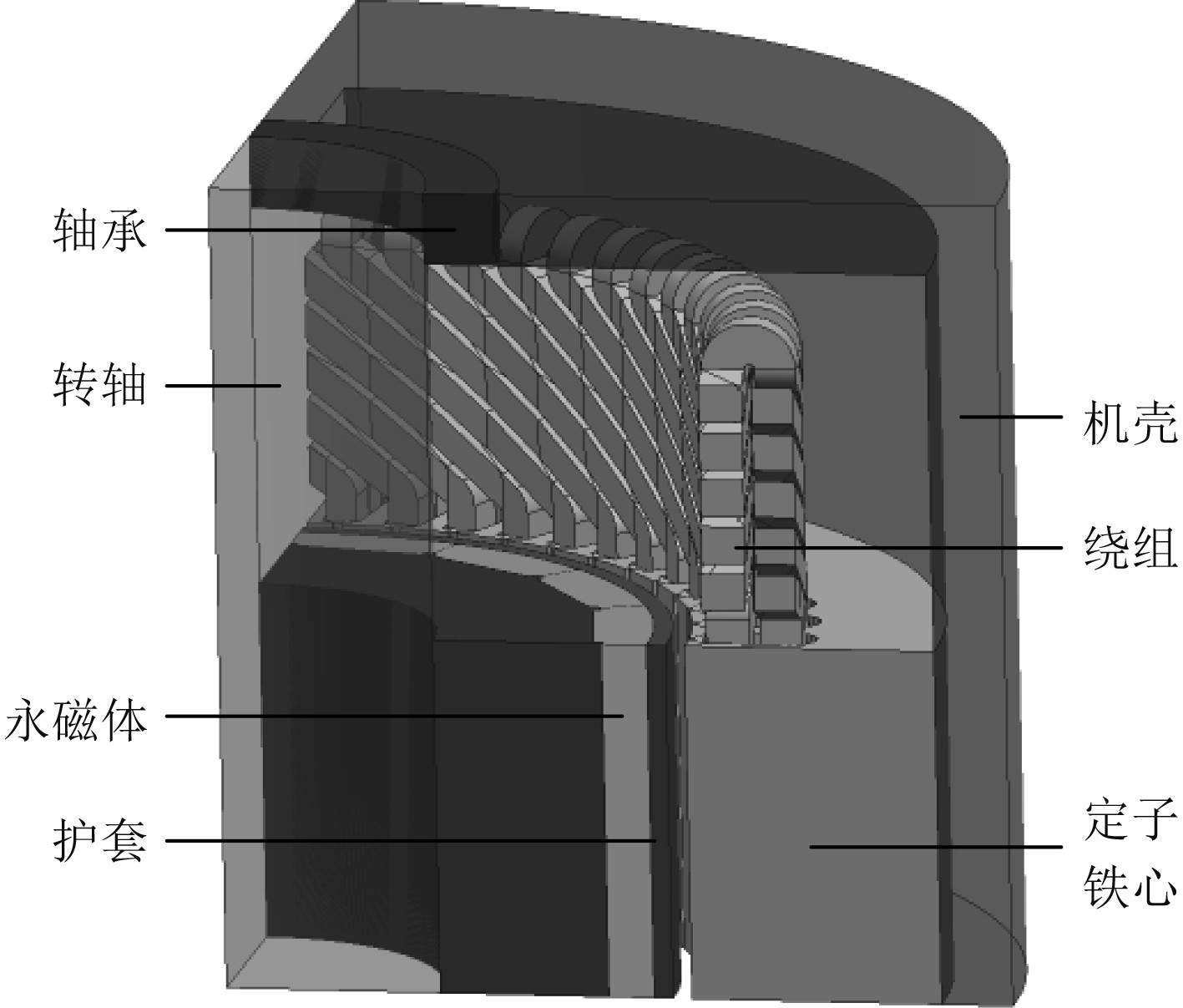
1 研究对象本文以1台4极48槽的表贴式永磁电机为例进行分析,该电机采用磁悬浮轴承作为支撑结构,电机内部密闭且保持真空状态,电机模型如图1所示,样机主要参数见表1。
|
图 1 电机模型 Fig. 1 Motor model |
|
|
表 1 电机主要参数 Tab.1 Main parameters of PMSM |
PCu为电机内的损耗主要包括绕组铜耗、PFe定子铁耗、PPM为永磁体涡流损耗,考虑到电机采用磁悬浮轴承且内部保持真空状态,可近似忽略电机转子的机械损耗和风摩损耗。
2.1 绕组铜耗本文所用分析样机最大工作频率约为667 Hz,对应的趋肤深度约为2.55 mm,电机采用多股直径为1 mm的Litz线并绕,由文献[11]可知,当导线半径小于工作频率对于的导体集肤深度时,可近似忽略由趋肤效应和邻近效应引起的铜耗。考虑铜导线电导率随温度变化,绕组铜耗可表示为:
| $ {P_{Cu}} = m\left[ {1 + {\alpha _c}(T - {T_0})} \right]{I^2}{R_{Cu}}({T_0}) 。$ | (1) |
式中:m为电机相数;
定子铁耗作为电机电磁损耗的主要组成部分,其精确计算对电磁场分析以及温度场的计算十分关键。传统的时步有限元法需要耗费大量的时间,为提高定子铁耗的计算效率,基于二维静磁场有限元分析并利用磁密的时空变换公式对定子铁耗进行求解[12]。
2.2.1 定子铁耗计算模型永磁电机中,电枢绕组和永磁体产生的旋转磁场可用傅里叶级数表示为时间t和空间机械角度θ的函数,磁密表达式如式(2)所示,式中未考虑电枢电流产生的空间谐波磁密。
| $ {B_g}(t,\theta ) = \sum\limits_{\nu = 1}^\infty {\left[ \begin{gathered} {B_{m\nu }}\sin (v\omega t + \nu p\theta ) \\ + {B_{a1}}\cos (\omega t + p\theta + {\varphi _0}) \\ \end{gathered} \right]}。$ | (2) |
式中:Bmv为永磁体产生的v次谐波磁密幅值,T;Ba1为电枢绕组产生的基波磁密幅值;ω为角频率,rad/s;p为极对数;φ0为电枢绕组磁密的初相角,rad。
时间变量t和空间变量θ可通过时空变换公式连接。
| $ p\theta = \omega t 。$ | (3) |
通过考虑定子铁心磁路的对称性,可知定子铁心磁密满足周期性条件:
| $ {B_{r,t}}(t,r,\theta ) = {B_{r,t}}(t + \frac{{pk{\theta _s}}}{\omega },r,\theta + k{\theta _s}) 。$ | (4) |
式中:θs为槽距角,rad;k为正整数。
基于上述理论基础,定子铁心中任意给定点(r,θ)处的磁密时间函数可通过固定时刻t下径向位置相同的中心对称点的磁密进行重新构建。
考虑到定子铁心内既存在交变磁化方式,又存在旋转磁化方式,故采用考虑旋转磁化影响的正交分解模型对定子铁耗进行求解[13],第i个单元考虑温升特性的铁耗表达式为:
| $ \Delta {P_i} = \Delta {m_i}\left\{ \begin{gathered} {k_h}f\sum\limits_{k = 1}^n {k(B_{kr}^2 + B_{k\theta }^2)} + \\ \frac{{{k_c}{f^2}}}{{1 + {\alpha _s}({T_1} - {T_0})}}\sum\limits_{k = 1}^n {{k^2}(B_{kr}^2 + B_{k\theta }^2)} \\ \end{gathered} \right\}。$ | (5) |
式中:Bkr,Bkθ分别为径向和切向磁密的k次谐波幅值,T;f为磁场交变频率,Hz;kh,kc分别为定子铁心磁滞,涡流损耗系数;αs为硅钢片电阻率的温度系数,1/K;
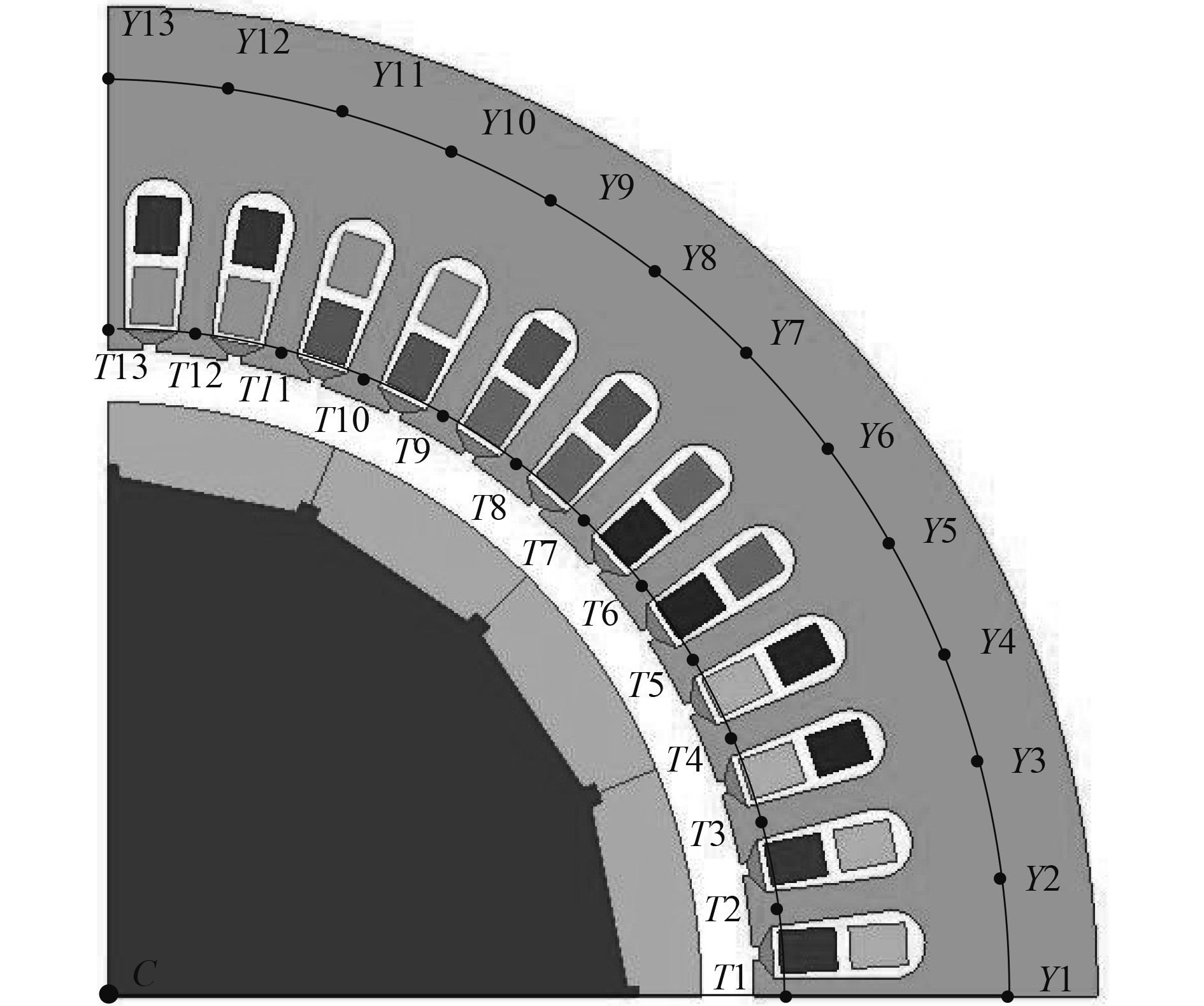
以表1所示的永磁电机为例对定子铁心损耗模型进行验证,样机二维有限元模型如图2所示。取齿部点(T1-T13,距C点104 mm)和轭部点(Y1-Y3,距C点140 mm)为样点进行时空变换,根据模型的对称边界条件,一个静磁场解可产生25个时刻的磁密信息。
|
图 2 样机有限元模型 Fig. 2 Example motor FEA model |
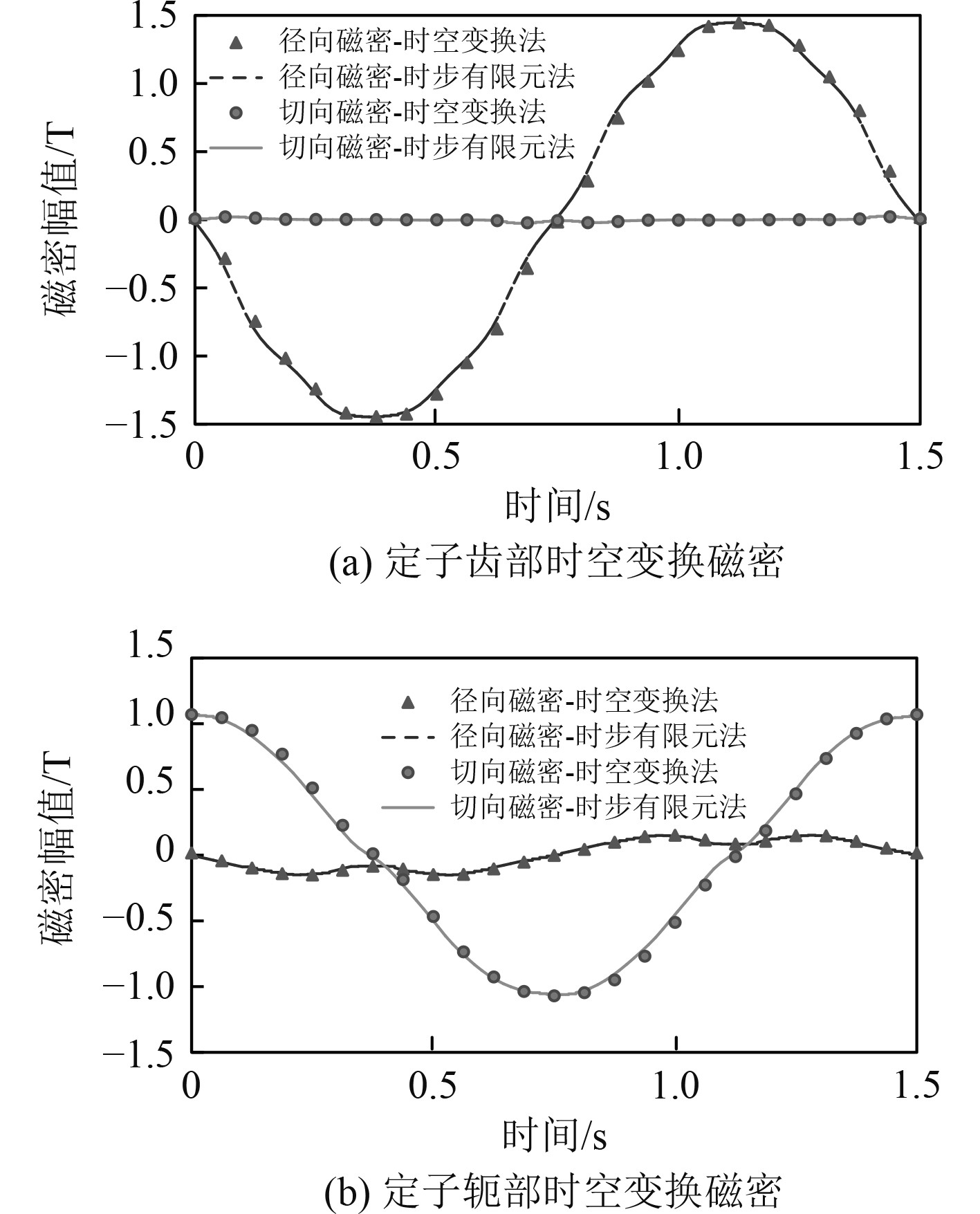
图3为由时空变换法与二维时步有限元法获得的定子齿部和轭部磁密的分析结果对比。可知,二者具有较好的一致性。
|
图 3 定子铁心时空变换磁密 Fig. 3 Stator space-time transformation flux density |
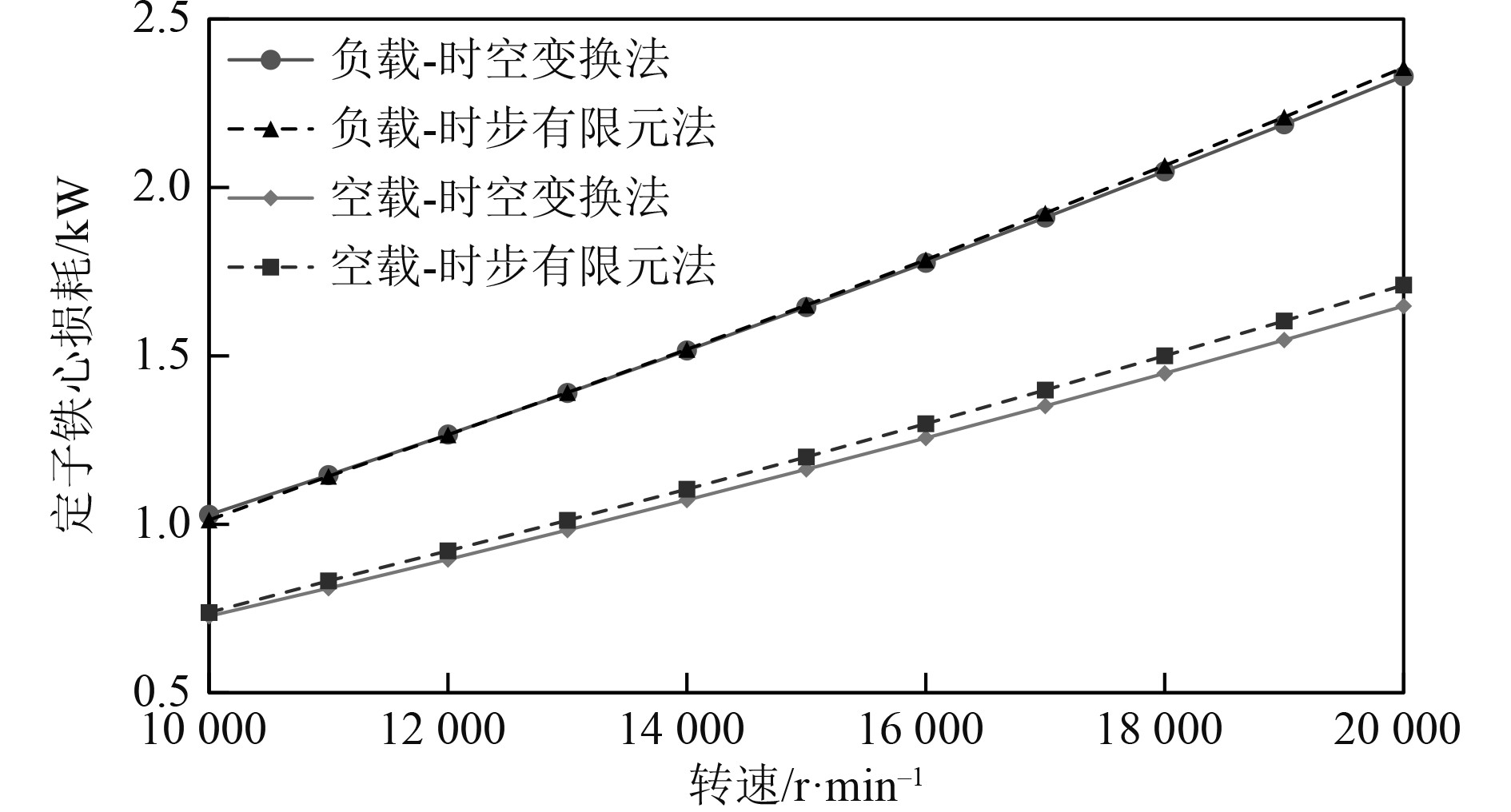
根据上述分析,可知仅需进行一次二维静磁场有限元分析即可对定子铁耗进行求解。空载及负载运行工况下的定子铁耗计算结果如图4所示。时空变换法计算结果与二维时步有限元的计算结果吻合度较好,表2给出了2种模型的参数对比及计算时间。可知2种模型虽然在网格划分上基本一致,但时空变换法的计算时间减少约79%。
|
图 4 空载与负载运行工况下的定子铁耗 Fig. 4 Core losses for the example motor of operating at unload and load, respectively |
|
|
表 2 模型参数及计算时间对比 Tab.2 Parameters and calculation time comparison |
本文研究对象虽然永磁体涡流损耗较小,但是电机内部有限的散热条件使得永磁体上会产生较大温升。通过时空变换公式获取永磁体内的磁密时间变化波形,再采用式(6)对永磁体涡流损耗进行计算[5]。
| $ {P_{eddy}} = \int\limits_V {\rho {J^2}} {\rm{d}}V,$ | (6) |
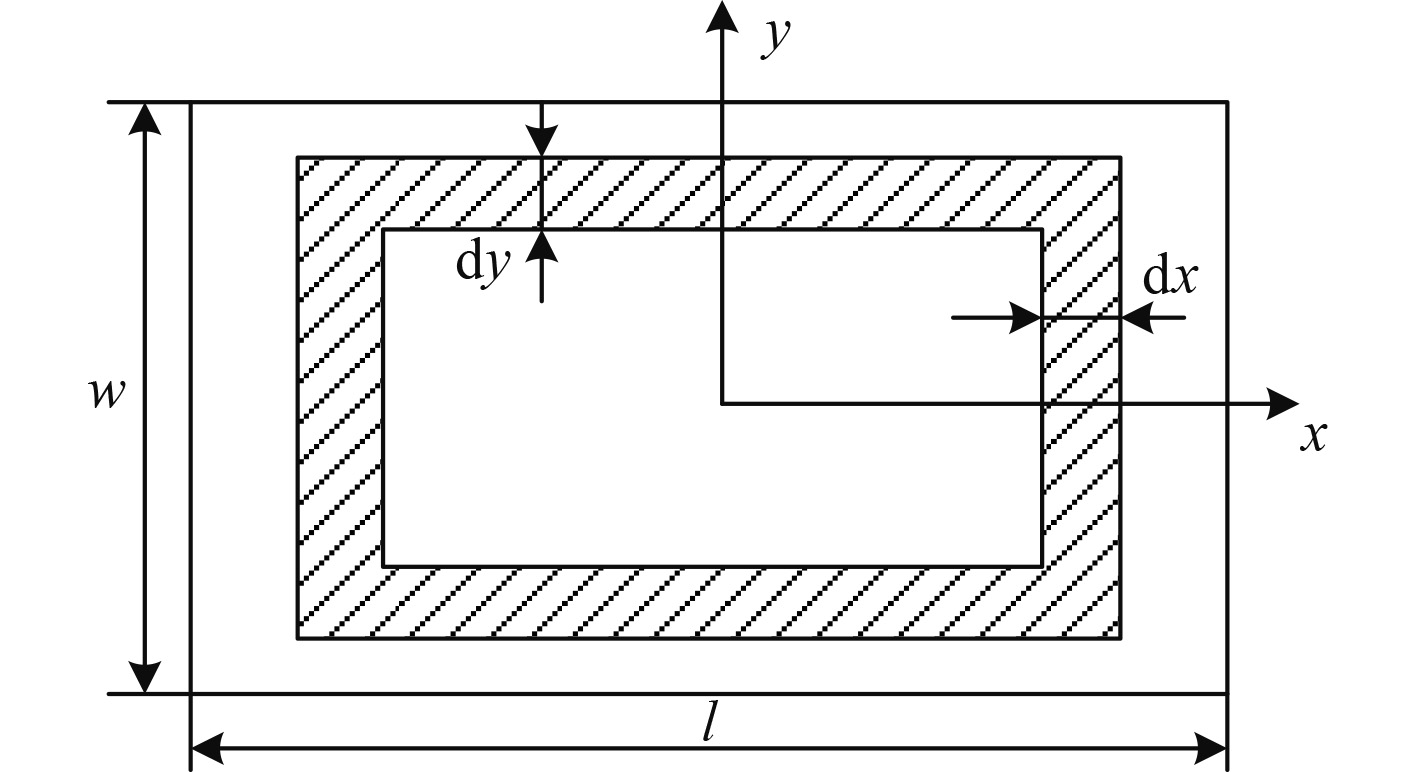
式中:ρ为永磁体的电阻率,Ω·m;J为涡流密度,A/m2。图5所示的永磁体涡流损耗计算模型,永磁体长为l,宽为w,厚度为h,涡流回路为图中阴影部分,涡流回路沿x轴和y轴方向宽度分别为dx和dy,涡流密度满足:
|
图 5 永磁体涡流损耗计算模型 Fig. 5 The calculation model of PM eddy loss |
| $ \left\{ {\begin{array}{*{20}{c}} {4x{J_x} + 4y{J_y} = - \dfrac{1}{\rho }\mathop B\limits^. xy} ,\\ {y = \dfrac{w}{l}x,{J_y} = \dfrac{w}{l}{J_x}} 。\end{array}} \right. $ | (7) |
式中:
由式(7)可得:
| $ \left\{ {\begin{array}{*{20}{c}} {{J_x} = - \dfrac{{\mathop {Bwl}\limits^. }}{{\rho ({l^2} + {w^2})}}x} ,\\ {{J_y} = - \dfrac{{\mathop {Bwl}\limits^. }}{{\rho ({l^2} + {w^2})}}y} 。\end{array}} \right. $ | (8) |
对电机温度场进行等效热网络分析和计算时,做出如下假设:
1)电机的温度场分布沿周向对称,且在周向上的冷却条件相同;
2)电机各电磁损耗均匀分布;
3)电机内部抽真空,忽略电机内部的对流散热。
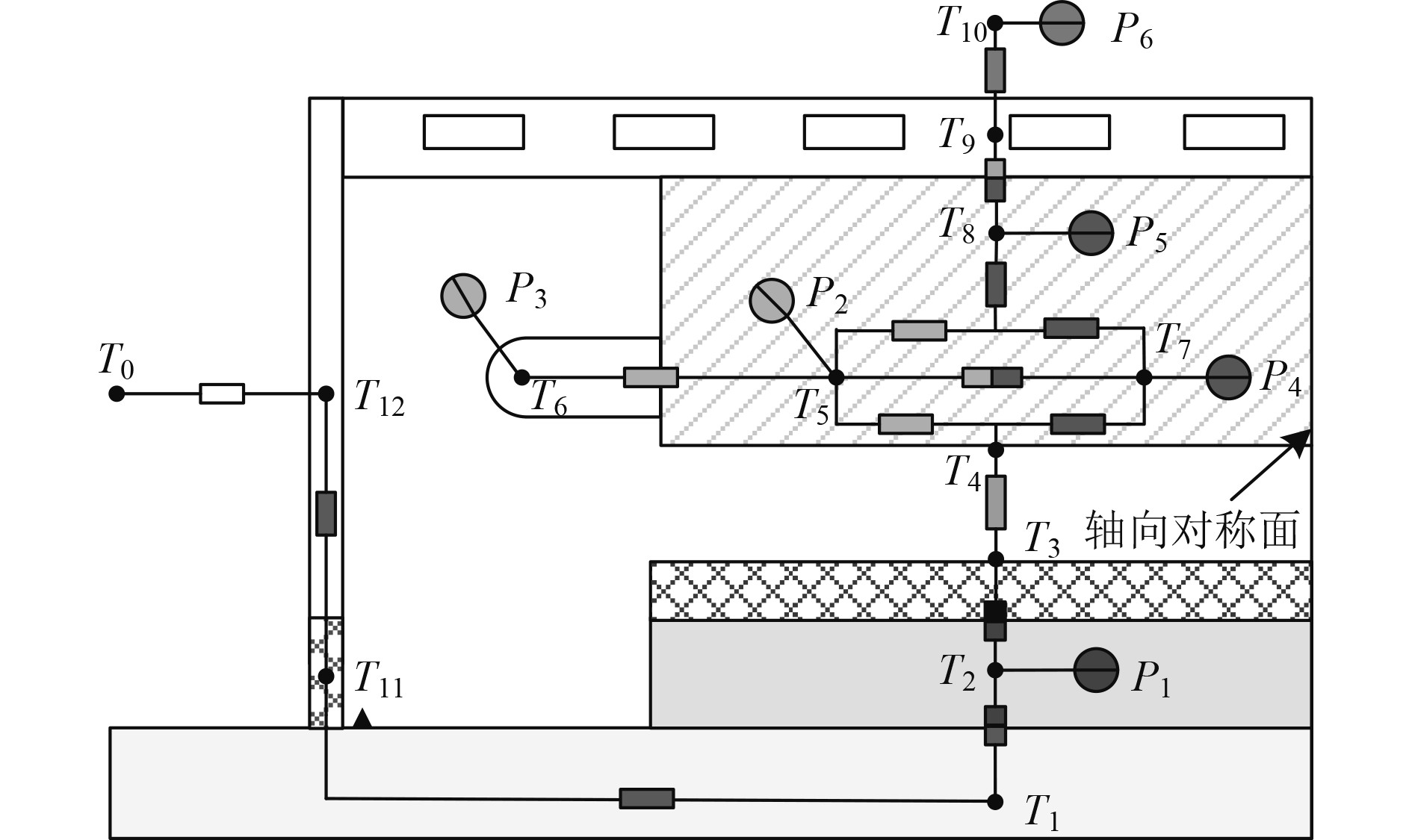
根据上述假设,可将电机内的温度场剖分成多个区域,各区域中心为温度节点,节点间用热阻联系起来,对电机沿轴向中心作对称处理,相应的等效热网络模型如图6所示。图中,T0为外部环境温度节点;T1转轴温度节点;T2为永磁体温度节点;T3、T4分别为转子外表面和定子内表面温度节点;T5,T6分别为槽内绕组和端部绕组温度节点;T7,T8分别为定子齿部和轭部温度节点;T10,T11分别为机壳和冷却液的温度节点;T12,T13分别为轴承和端盖的温度节点;P1为永磁体涡流损耗、P2,P3分别为槽内绕组和端部绕组的铜耗;P4,P5分别为定子齿部和轭部铁耗;P6为冷却液散热功率。
|
图 6 电机等效热网络模型 Fig. 6 Equivalent thermal network model of motor |
电机内的传热过程主要包括热传导和热辐射,对应的热阻为传导热阻和辐射散热热阻[14]。对于热传导,根据傅里叶定律,满足:
| $ {q_x} = - \lambda \frac{{{\rm{d}}\theta }}{{{\rm{d}}x}}。$ | (9) |
式中:qx为热传导的热流密度,W/m2;λ为材料的热导率,W/m/K;dθ/dx为温度梯度,K/m。
对于辐射散热,按辐射定律,每秒从每平方米发热体表面辐射出去的热量为:
| $ {q_r} = \sigma \varepsilon \cdot VF({T^4} - T_0^4)。$ | (10) |
式中:σ为斯蒂芬-玻尔兹曼常数,σ=5.67×10−8W/(m2·K4);ε为辐射换热面的辐射率;VF为辐射角系数;T、T0分别为发热体表面和周围介质的绝对温度,K。
根据电机热网络模型,建立节点瞬态温升状态空间方程,各节点x的温度随时间的变化如式(11)所示,当时间趋近于无穷大时即可获得节点的稳态温升。
| $ \frac{{{\rm{d}}{\theta _x}}}{{{\rm{d}}t}} = \frac{1}{{{C_x}}}\left[ { - {\theta _x}\left(\sum {\frac{1}{{{R_{x,y}}}}} \right) + \left(\sum {{\theta _y} \cdot \frac{1}{{{R_{x,y}}}}} \right)} \right] + \frac{1}{{{C_x}}}{P_x} 。$ | (11) |
式中:Rx,y为节点x和节点y之间的热阻,K/W;C为节点热容,J/K;P为节点输入损耗,W。
上式可转化为状态空间方程形式:
| $ \left\{ \begin{gathered} \mathop \theta \limits^ \cdot (t) = {\boldsymbol{A}}\theta (t) + {\boldsymbol{B}}P(t) ,\\ y(t) = \theta (t)。\\ \end{gathered} \right. $ | (12) |
其中:
| $ \begin{split} & {\boldsymbol{A}} = \left( {\begin{array}{*{20}{c}} {\dfrac{1}{{{C_1}}}} \\ \vdots \\ {\dfrac{1}{{{C_n}}}} \end{array}} \right) \cdot \left[ {\begin{array}{*{20}{c}} { - \sum\limits_{i = 1}^n {\dfrac{1}{{{R_{1,i}}}}} }&{\dfrac{1}{{{R_{1,2}}}}}& \cdots &{\dfrac{1}{{{R_{1,n}}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\dfrac{1}{{{R_{n,1}}}}}&{\dfrac{1}{{{R_{n,2}}}}}& \cdots &{ - \sum\limits_{i = 1}^n {\dfrac{1}{{{R_{n,i}}}}} } \end{array}} \right] \text{,}\\ & {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{C_1}}}}&0& \cdots &0 \\ 0& \vdots & \ddots & \vdots \\ 0&0& \cdots &{\dfrac{1}{{{C_n}}}} \end{array}} \right] 。\\[-35pt] \end{split} $ | (13) |
电机内的传导热阻主要考虑接触热阻及各部件内部的传导热阻。
接触热阻是由于接触面的缺陷或装配造成的,2个相邻固体间的接触热阻可以由下式计算:
| $ {R_{cond}} = \frac{{{l_i}}}{{{k_{air}}{A_i}}}。$ | (14) |
式中:
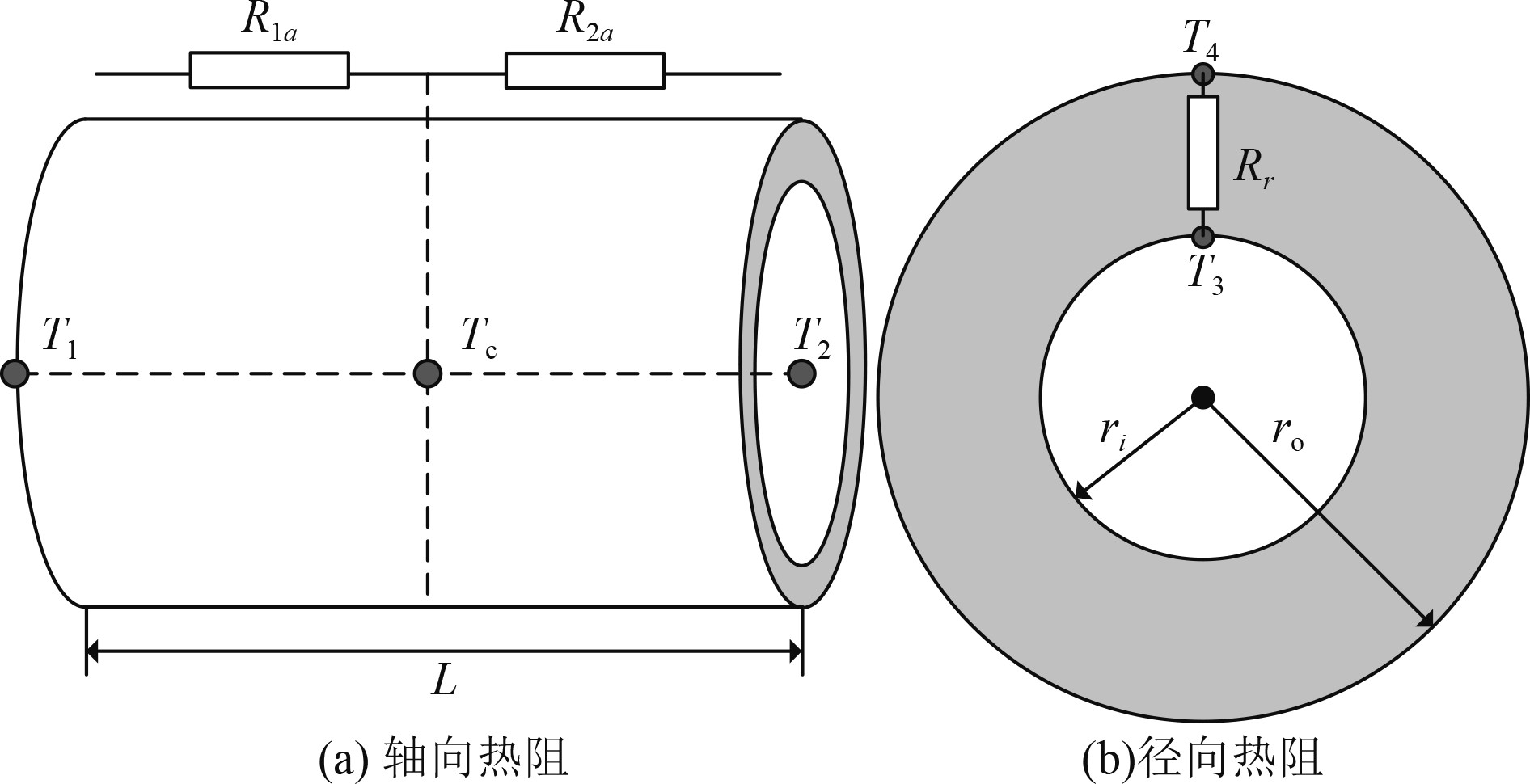
对于各部件内部的传导热阻,主要是基于文献[15]提出的圆柱形热阻模型,电机中大部分固体部件都可认为是圆柱形,圆柱形组件的轴向和径向等效热阻模型如图7所示。
|
图 7 圆柱形部件的内部传导热阻模型 Fig. 7 Heat resistance of a hollow cylinder |
轴向传导热阻可由下式计算:
| $ \left\{ \begin{aligned} & {{R_{1a}} = \frac{L}{{2\text{π} {h_{ca}}(r_o^2 - r_i^2)}}},\\ & {{R_{2a}} = \frac{L}{{2\text{π} {h_{ca}}(r_o^2 - r_i^2)}}} 。\end{aligned} \right. $ | (15) |
式中:ro、ri分别为圆柱形部件的外径和内径,m;L为轴向长度,m;hca为轴向导热系数,W/m/K。
径向传导热阻可由下式计算:
| $ {R_r} = \frac{{\ln \dfrac{{{r_o}}}{{{r_i}}}}}{{2 \text{π} {h_{cr}}L}}。$ | (16) |
式中:
电机的辐射散热主要可以分为两部分:一是电机内部的辐射散热,例如转子外表面与定子内表面间的辐射散热;二是电机外部的辐射散热,例如机壳与外部环境间的辐射散热。
表面1、表面2间的辐射热阻为:
| $ {R_{12}} = \frac{1}{{{A_1} \cdot {h_{12}}}} = {R_{21}} = \frac{1}{{{A_2} \cdot {h_{21}}}}。$ | (17) |
式中:A1、A2分别为表面1、表面2的面积,m2;h12,h21分别为表面1、表面2的辐射散热系数,W/m2/K。
对于内部辐射散热,辐射散热系数表达式为:
| $ \left\{ \begin{aligned} & {{h_{12}} = \sigma \cdot {F_{12}}\frac{{(T_1^4 - T_2^4)}}{{{T_1} - {T_2}}}},\\ & {{h_{21}} = \sigma \cdot {F_{21}}\frac{{(T_2^4 - T_1^4)}}{{{T_2} - {T_1}}}} 。\end{aligned} \right. $ | (18) |
式中:T1、T2为表面1、表面2的绝对温度,K;F12、F21为表面1、表面2的辐射散热因子,满足:
| $ \left\{ \begin{aligned} & {\frac{1}{{{F_{12}}}} = \frac{1}{{VF}} + \left(\frac{1}{{{\varepsilon _1}}} - 1\right) + \frac{{{A_1}}}{{{A_2}}}\left(\frac{1}{{{\varepsilon _2}}} - 1\right)},\\ & {{A_1}{F_{12}} = {A_2}{F_{21}}} 。\end{aligned} \right. $ | (19) |
式中:
外部辐射散热系数的计算公式为:
| $ {h_r} = \sigma {\varepsilon _r} \cdot VF\frac{{(T_n^4 - T_a^4)}}{{{T_n} - {T_a}}} 。$ | (20) |
式中:εr为机壳表面辐射率;
在电路中,电容阻碍电压的变化并且储存电能,类比到热路中,热容抑制温度的变化并且能够储存热能,热容计算表达式为:
| $ {C_h} = \rho Vc。$ | (21) |
式中:
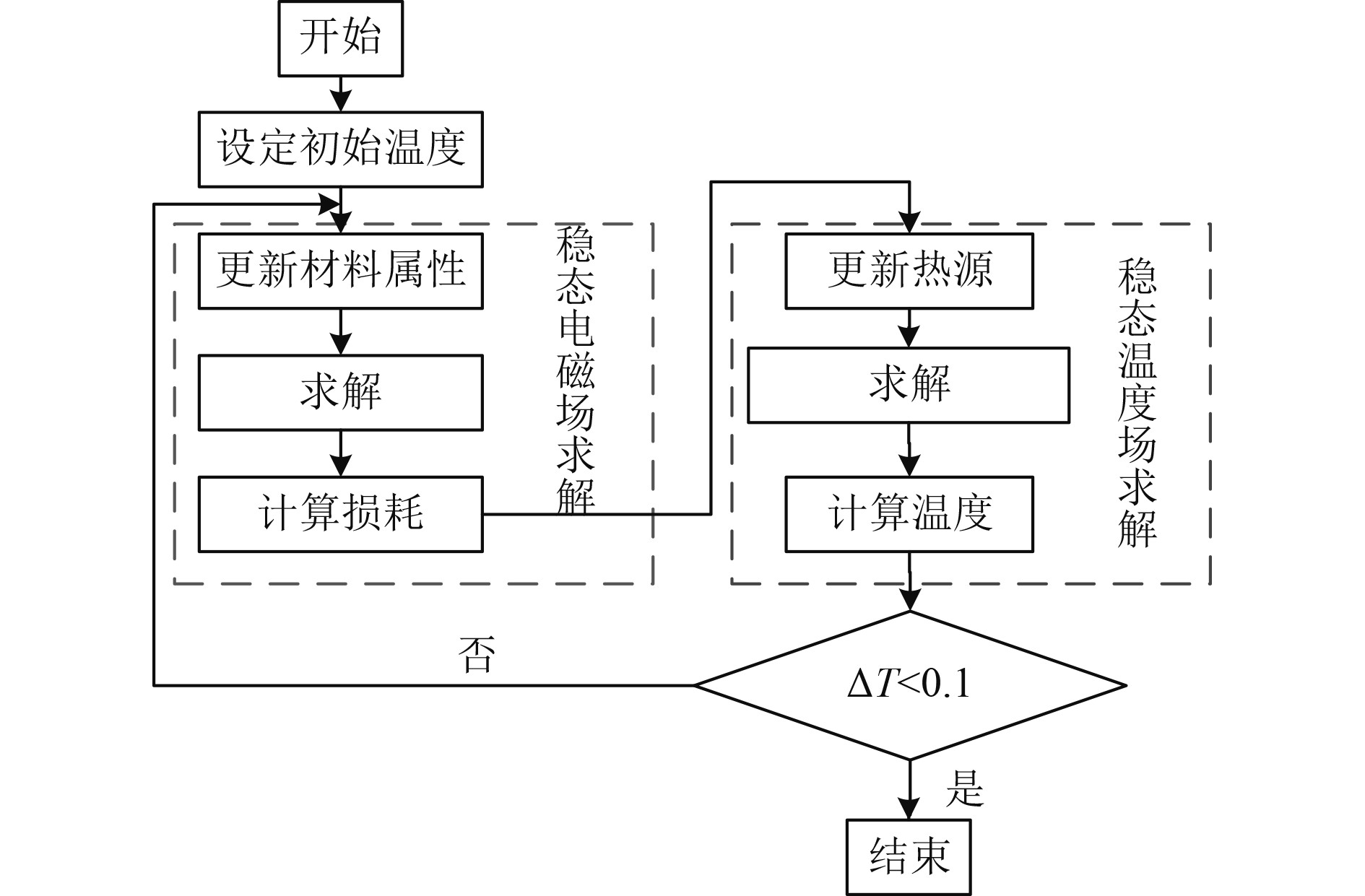
永磁电机电磁场时间常数远小于温度场,所以永磁电机电磁热耦合计算一般采用交替迭代的方式进行求解,求解流程如图8所示。根据初始温度计算电磁损耗,将电磁损耗作为热源输入热网络模型进行温度场求解。然后,根据温度更新材料属性重新进行电磁损耗计算,如此交替迭代,直至收敛。在本文中,若前后2次迭代中永磁体和绕组平均温差小于0.1 K,则认为收敛。
|
图 8 电机电磁热耦合计算流程 Fig. 8 Procedure of coupling algorithm for steady state electromagnetic-thermal analysis |
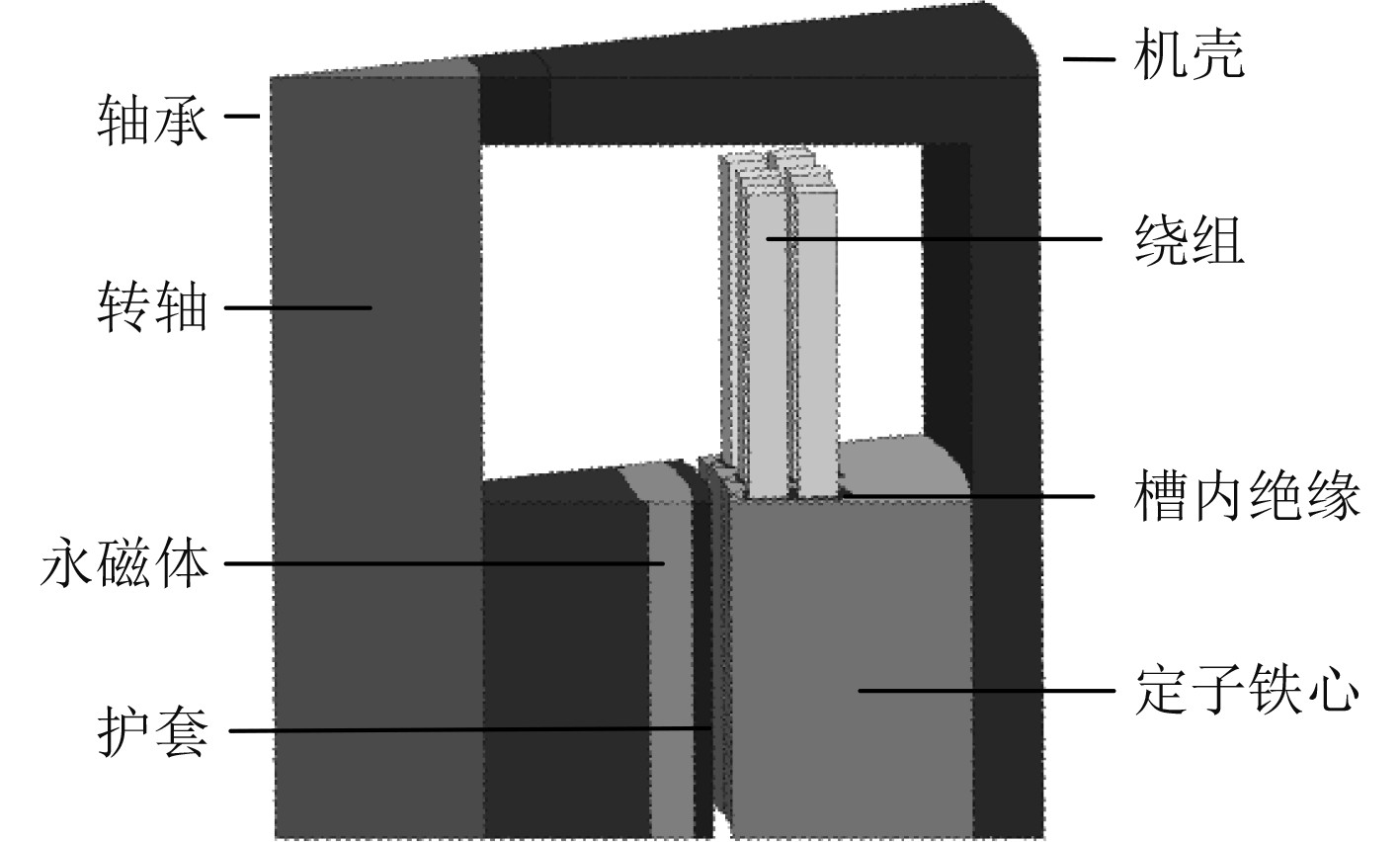
为验证本文模型的准确性以及计算效率,选取表1所示永磁电机的轴向1/2和周向1/16建立三维有限元耦合模型进行对比,模型如图9所示。绕组端部由直线等效,且假定电机各相邻部件紧密接触,为了模拟电机机壳水冷,电机机壳温度设定为恒定值40℃。
|
图 9 温度场三维有限元分析模型 Fig. 9 3D thermal FEA model |
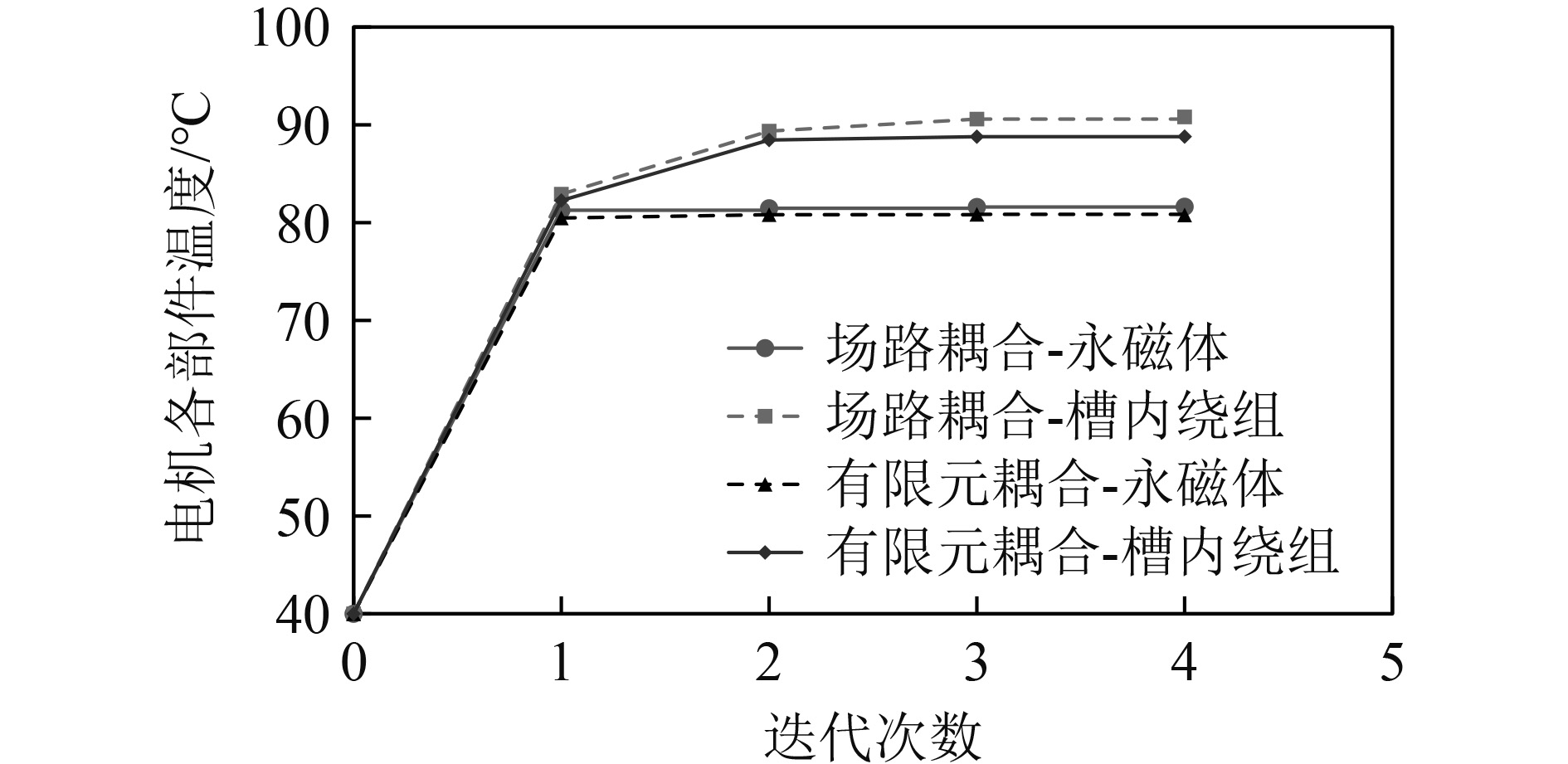
2种耦合模型计算得到永磁体与槽内绕组平均温升随迭代次数变化情况如图10所示。可知,当迭代次数为4时,耦合场计算已经收敛。
|
图 10 电机各部件温度随迭代次数的变化 Fig. 10 Variation of component temperature with iteration number |
收敛后的计算结果对比如表3所示。可知,场路耦合模型的计算时间远小于有限元耦合模型,时间缩短约95.2%,且二者计算结果具有较好的一致性,最大计算误差约为5.3 K,验证了所建立的电磁热耦合模型的有效性。
|
|
表 3 模型计算结果对比 Tab.3 Temperature result of various components |
本文基于二维静磁场有限元模型与等效热网络模型建立了永磁电机的电磁热耦合分析模型,得到的主要结论如下:
1)对时空变换法的原理进行理论分析,并以此为基础建立了永磁电机电磁损耗的计算模型,相同硬件条件下,与二维时步有限元法相比,计算时间减少约79%。
2)基于传热学定律建立了电机的等效热网络模型,并推导了节点稳态和瞬态温升计算的状态空间方程,降低了建模难度和求解时间。
3)将建立的场路耦合模型与三维有限元耦合模型进行对比,温度场计算结果最大误差为5.3 K,计算时间减少约95.2%,表明本文所建立的电磁热耦合模型可在保证计算精度的前提下提高电磁热耦合分析效率。
| [1] |
李勇, 吴佳鑫, 马鹏程, 等. 飞行器用永磁电机系统的功率密度与需求展望[J]. 电机与控制学报, 2022, 26(2): 1-9. LI Yong, WU Jia-xin, MA Peng-cheng, et al. Analysis of power density and prospects of future technology requirement of permanent magnet motors used in aircrafts[J]. Electric Machines and Control, 2022, 26(2): 1-9. |
| [2] |
王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(S1): 22-29. WANG Xiao-fei, DAI Yin, LUO Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29. |
| [3] |
付兰芳, 孙鹤旭, 王华君, 等. 基于永磁双转子电机调速的新型风力发电系统设计[J]. 电力系统自动化, 2014, 38(15): 25-29. FU Lan-fang, SUN He-xu, WANG Hua-jun, et al. Design of a novel wind power generation system based on speed regulation of permanent magnet double-rotor motor[J]. Automation of Electric Power Systems, 2014, 38(15): 25-29. |
| [4] |
鲍海静. 飞轮储能用高速永磁同步电机设计及关键技术研究 [D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [5] |
陈萍, 唐任远, 佟文明, 等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6): 1-9. CHEN Pin, TANG Ren-yuan, TONG Wen-min, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9. |
| [6] |
董剑宁, 黄允凯, 金龙, 等. 高速永磁电机设计与分析技术综述[J]. 中国电机工程报, 2014, 34(27): 4640-4653. DONG Jian-ning, HUANG Yun-kai, JIN Long, et al. Review on high speed permanent magnet machines including design and analysis technologies[J]. Proceedings of the CSEE, 2014, 34(27): 4640-4653. |
| [7] |
VESE I C, MARIGNETTI F, Radulescu M M. Multiphysics approach to numerical modeling of a permanent-magnet tubular linear motor[J]. IEEE Transactions on Industrial Electronics, 2009, 57(1): 320-326. |
| [8] |
JOO D, CHO J H, WOO K, et al. Electromagnetic field and thermal linked analysis of interior permanent-magnet synchronous motor for agricultural electric vehicle[J]. IEEE transactions on magnetics, 2011, 47(10): 4242-4245. DOI:10.1109/TMAG.2011.2149504 |
| [9] |
韩雪岩, 张华伟, 贾建国, 等. 基于等效热网络法的轴向磁通永磁电机热分析[J]. 微电机, 2016, 49(4): 6-10. HAN Xue-yan, ZHANG Hua-wei, JIA Jian-guo, et al. Thermal analysis of axial flux permanent magnet motor based on equivalent thermal network method[J]. Micromotors, 2016, 49(4): 6-10. |
| [10] |
LI G J, OJEDA J, HOANG E, et al. Comparative studies between classical and mutually coupled switched reluctance motors using thermal-electromagnetic analysis for driving cycles[J]. IEEE Transactions on magnetics, 2011, 47(4): 839-847. DOI:10.1109/TMAG.2011.2104968 |
| [11] |
GONZALEZ D A, SABAN D M. Study of the copper losses in a high-speed permanent-magnet machine with form-wound windings[J]. IEEE Transactions on Industrial Electronics, 2013, 61(6): 3038-3045. |
| [12] |
IONEL D M, POPESCU M. Ultrafast finite-element analysis of brushless PM machines based on space–time transformations[J]. IEEE Transactions on Industry Applications, 2010, 47(2): 744-753. |
| [13] |
黄允凯, 胡虔生, 朱建国. 永磁无刷直流电机铁耗计算方法[J]. 电机与控制应用, 2007(4): 6-9. HUANG Yun-kai, HU Qian-sheng, ZHU Jian-guo. Methods for calculating core losses in permanent magnet motors[J]. Electric Machines & Control Application, 2007(4): 6-9. DOI:10.3969/j.issn.1673-6540.2007.04.002 |
| [14] |
王晓远, 高鹏. 等效热网络法和有限元法在轮毂电机温度场计算中的应用[J]. 电工技术学报, 2016, 31(16): 26-33. WANG Xiao-yuan, GAO Peng. Application of equivalent thermal network method and finite element method in temperature calculation of in-wheel motor[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 26-33. |
| [15] |
MELLOR P H, ROBERTS D, TURNER D R. Lumped parameter thermal model for electrical machines of TEFC design[C]//IEE Proceedings B (Electric Power Applications). IET Digital Library, 1991, 138(5): 205–218.
|
 2023, Vol. 45
2023, Vol. 45
