船舶电力系统所获得的优势引起了人们对全电力船舶日益浓厚的兴趣[1-2]。相对于交流电力系统,直流电力系统更适合用于船舶,优势在于直流电力系统主母线不受与之连接的同步发电机频率限制,而且节省空间和重量,设备布置灵活[3-4]。作为发电原动机的微型燃气轮机具有高功率密度、高可靠性、高效率、低维护、低排放等特点,在船舶电力系统、分布式能源等领域应用非常广泛[5-6]。
船舶电力系统是一个独立的发电系统,极易受冲击载荷的影响[7]。船舶上各种大功率电气设备逐渐增加,大功率设备在投切时会引起瞬时的负载突变[8-9]。而解决冲击负载问题的理想方法是在原动机末端进行调节,这要求燃气轮机发电系统(Micro Turbine Generation System,MTGS)必须具备输出功率的快速调节能力。然而,由于燃气轮机燃烧机制缓慢,输出机械功率的响应很慢。这种较慢的响应特性使之抗冲击负载的能力较差,因此研究基于瞬时功率平衡的解决方案。
目前解决电网负载不平衡最有效的途径是在电网中增加储能装置[10-11],利用储能装置的功率特性进行快速的充放电以解决原动机输出功率响应慢的问题。目前,典型的储能装置包括飞轮储能、超级电容器储能、电池储能等[12-13]。相比于其他储能,飞轮储能系统(Flywheel Energy Storage System,FESS)具有能量密度高、工作温度范围宽、瞬态响应快、可靠性高、使用寿命长、经济效益好等显著特点[14]。飞轮储能的高功率动态响应可弥补燃气轮机低动态响应问题,平衡系统瞬态下的功率,维持直流母线电压在稳定范围内,增强MTGS对冲击性负荷的适应性。因此,FESS的应用可较好地解决船舶电力系统冲击负载的问题。
Saleh等[15]提出一种新型的微电网飞轮储能拓扑结构,将飞轮储能连接在燃料电池和光伏逆变器的同一直流母线上,而不是与单独的并网逆变器连接,研究表明FESS能够承受负荷、光伏和风力的变化,提高了微电网内部的功率因素。刘永葆等[16]将飞轮储能应用于燃气轮机发电系统,关注微型燃气轮机转速、交流电网电压和发电机功率的变化。其研究对象是交流电力系统,没有关注对直流母线电压的影响。邱子鉴等[17]以光伏微电网为基础,分析了功率波动产生的原因以及蓄电池和超级电容的充放电特性,用储能系统平抑光伏并网引起的波动以提高电能质量,最终提出了一种改进的模糊下垂控制策略,通过对下垂系数的快速调整实现对变换器输出量的动态控制。支娜等[18]以抑制直流微电网离网模式下母线电压的波动为目的,以虚拟直流电机为切入点,通过分析小信号模型得出母线电压出现稳态误差的原因,阻尼系数越大对母线的影响越严重,针对此问题提出一种储能变换器改进虚拟直流电机控制策略可消除因阻尼系数变化对母线造成的影响。梁明玉等[19]针对微电网并网与孤岛运行模式切换产生的冲击问题,提出一种改进的下垂控制策略,此策略的下垂系数会随实际输出功率的变化而做出相应调整,之后通过搭建仿真验证了该策略的可行性。
当前关于微电网储能系统与发电单元之间的控制策略优化研究,主要针对以新能源为主的交流微电网。其中储能系统一般用于平抑并网和孤岛模式切换时引起的波动以提高电能质量,而对以燃气轮机发电机组为主体的船舶直流微电网以及大功率负载投切对电力系统稳定性影响的研究较少。船舶直流微电网有其独特的性能,区别于交流微电网复杂的电能变换环节,直流微电网电能变换环节少,系统结构简单,运行效率得以提升,且直流电网不考虑交流电中含有的无功分量和频率的问题,简化了控制系统。同时,船舶直流负载的应用日益普遍,且单装备、单系统功率不断增加,大功率负载的投切会对船舶电力系统造成明显冲击。因此,研究直流微电网系统的负载冲击和稳定性能是本领域现实而迫切的问题。本文以带有FESS的MTGS直流微电网为研究对象,设计FESS的控制策略,突加、突卸大功率负载,研究直流母线电压和同步发电机转速的变化特性,分析FESS的应用对电网和燃气轮机发电机组波动的平抑效果。
为更好地研究带有FESS的MTGS在冲击负荷作用下的瞬态稳定性,本文基于实际的100
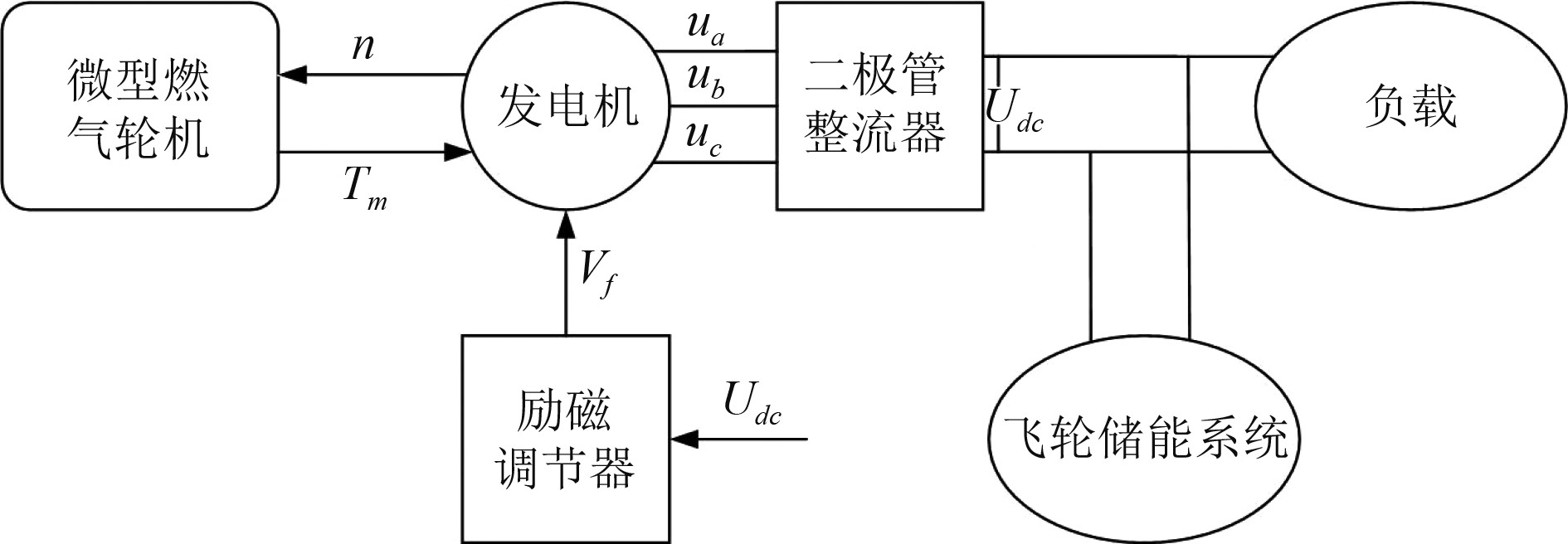
本文所建MTGS整体模型如图1所示。该系统模型由微型燃气轮机、带有励磁系统的三相同步发电机、二极管整流器、阻性负载和FESS组成。微型燃气轮机输出机械扭矩
|
图 1 微型燃气轮机发电系统整体模型 Fig. 1 Overall model of a micro gas turbine power generation system |
微型燃气轮机作为主动力装置,驱动发电机发电。本文以现有的100
1)压气机模型
压气机的特征参数有折合流量
| $ {p_{c{\rm{out}}}} = {p_{c{\rm{in}}}} \cdot {\pi _c}。$ | (1) |
式中:
利用在压气机特性图上插值的方法可求得:
| $ {G_{cnp}} = {f_1}({n_{cnp}},{\pi _c}) ,$ | (2) |
| $ {\eta _c} = {f_2}({n_{cnp}},{G_{cnp}})。$ | (3) |
进一步可计算出压气机流量
| $ {G_c} \cdot \sqrt {\frac{{{T_{c{\rm{in}}}}}}{{{T_1}}}} = {G_{cnp}} \cdot \frac{{{P_{c{\rm{in}}}}}}{{{P_1}}},$ | (4) |
| $ {T_{c{\rm{out}}}} = {T_{c{\rm{in}}}} \cdot \left(1 + \frac{{{\pi ^{\frac{{{k_a} - 1}}{{{k_a}}}}} - 1}}{{{\eta _c}}}\right),$ | (5) |
| $ N{e_c} = {h_{c{\rm{out}}}} - {h_{c{\rm{in}}}} 。$ | (6) |
式中:
2)燃烧室模型
燃烧室的数学模型可表示为:
| $ {p_{bout}} = {p_{bin}} \cdot \sigma,$ | (7) |
| $ b = \frac{{{G_f}}}{{{G_{bin}}}}\frac{{{\mu _{air}}}}{{{\mu _r}}} \times 57.57 。$ | (8) |
式中:
3)涡轮模型
涡轮的效率
| $ {\pi _t} = \frac{{{p_{tin}}}}{{{p_{tout}}}}。$ | (9) |
利用在涡轮特性图上插值的方法可求得:
| $ {G_{tnp}} = {f_1}({n_{tnp}},{\pi _t}) ,$ | (10) |
| $ {\eta _t} = {f_2}({n_{tnp}},{G_{tnp}})。$ | (11) |
进一步可计算出涡轮出口温度
| $ {T_{tout}} = {T_{tin}} \cdot \left(1 - \left(1 - {{\pi }_t^{ - \frac{{{k_b} - 1}}{{{k_b}}}}}\right) \cdot {\eta _t}\right),$ | (12) |
| $ N{e_t} = {h_{tin}} - {h_{tout}} 。$ | (13) |
式中:
4)转子模型
转子是将压气机和涡轮以及负载连接起来的装置,涡轮输出的功率用来带动压气机转动以及带动发电机运行。在不考虑机械损耗的情况下,根据动量矩定律可获得转子的数学模型。
| $ \frac{{{\rm{d}}n}}{{{\rm{d}}t}} = \frac{{900}}{{J{\text{π} ^2}n}}({N_{et}} - {N_{ec}} - {P_G}) 。$ | (14) |
式中:
同步发电机在dqo坐标系下的电压、磁链和转矩方程分别为:
| $ \left\{ \begin{gathered} {u_d} \\ {d_q} \\ {u_0} \\ {u_f} \\ {u_D}( = 0) \\ {u_Q}( = 0) \\ \end{gathered} \right\} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left\{ \begin{gathered} {\psi _d} \\ {\psi _q} \\ {\psi _0} \\ {\psi _f} \\ {\psi _D} \\ {\psi _Q} \\ \end{gathered} \right\} + \left\{ \begin{gathered} - \omega {\psi _q} \\ \omega {\psi _d} \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{gathered} \right\} + \left\{ \begin{gathered} - {r_a}{i_d} \\ - {r_a}{i_q} \\ - {r_a}{i_n} \\ {r_f}{i_f} \\ {r_D}{i_D} \\ {r_Q}{i_Q} \\ \end{gathered} \right\},$ | (15) |
| $ \left\{ \begin{gathered} {\psi _d} \\ {\psi _q} \\ {\psi _0} \\ {\psi _f} \\ {\psi _D} \\ {\psi _Q} \\ \end{gathered} \right\} = \left\{ \begin{array}{lllllllll} {X_d}& 0 &0 &{{\text{X}}_{ad}} & {{\text{X}}_{ad}} &{\text{ 0}} \\ 0 & {X_q} & 0 &0 & 0 & {{\text{X}}_{aq}} \\ 0 &{\text{ 0 }} &{X_0} & 0 & 0 &{\text{ 0}} \\ {{\text{X}}_{ad}} & 0 &0 &{{\text{X}}_f} & {{\text{X}}_{ad}} &{\text{ 0}} \\ {{\text{X}}_{ad}} & 0 &0 &{{\text{X}}_{ad}} & {{\text{X}}_D} &{\text{ 0}} \\ 0 & {{\text{X}}_{aq}} &{\text{ 0 }} &0 & 0 & {{\text{X}}_{\text{Q}}} \\ \end{array} \right\}\left\{ \begin{gathered} - {i_d} \\ - {i_q} \\ - {i_0} \\ {i_f} \\ {i_D} \\ {i_Q} \\ \end{gathered} \right\},$ | (16) |
| $ {T_e} = {\psi _d}{i_d} - {\psi _q}{i_q} 。$ | (17) |
式中:
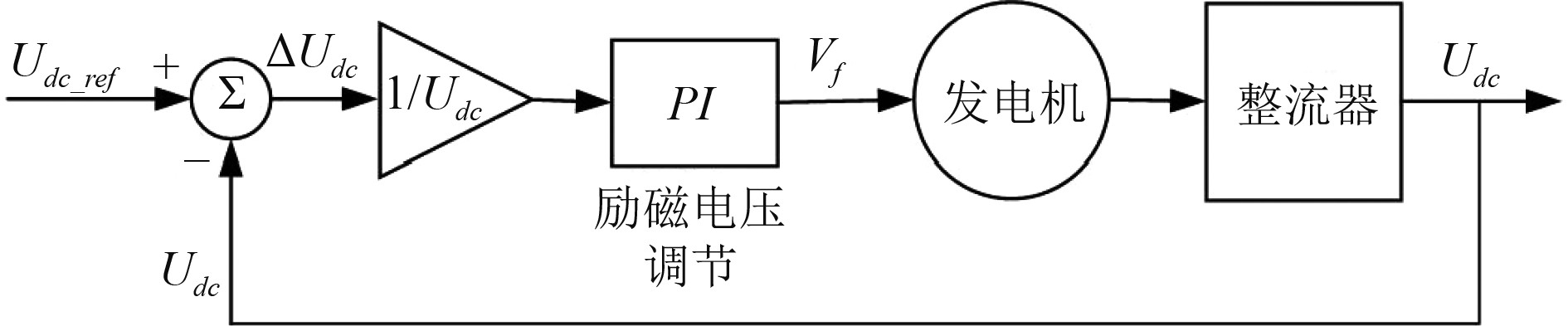
同步发电机不带直流负载时,一般将发电机交流侧电压进行反馈,用于对励磁电压的调节。带直流负载时,由于交流侧电压畸变较大,且整流器存在换向压降,即使准确地调节了交流测侧电压的大小,也不能保证对直流母线电压的准确控制。因此,采用将直流侧滤波电容电压作为反馈量对励磁电压进行调节,进而实现对发电机的端电压的调节[21]。励磁控制原理如图2所示。
|
图 2 直流励磁控制系统模型 Fig. 2 Model of the DC excitation control system |
实际的直流母线电压
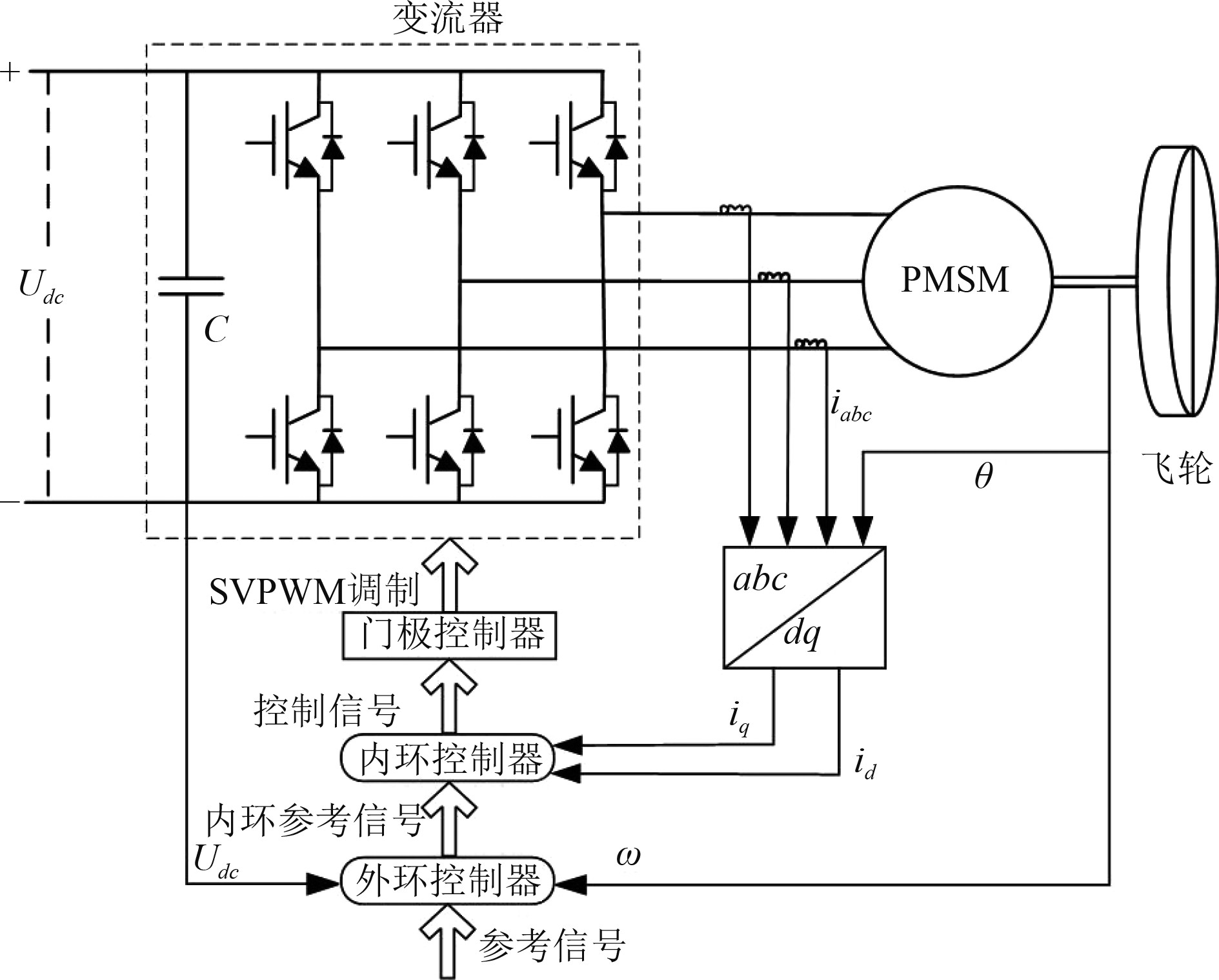
参考交流微电网FESS,搭建直流微电网FESS,如图3所示。FESS由3个主要部分组成:变流器、永磁同步电机和飞轮。
|
图 3 飞轮储能系统拓扑结构 Fig. 3 Topological structure of the flywheel energy storage system |
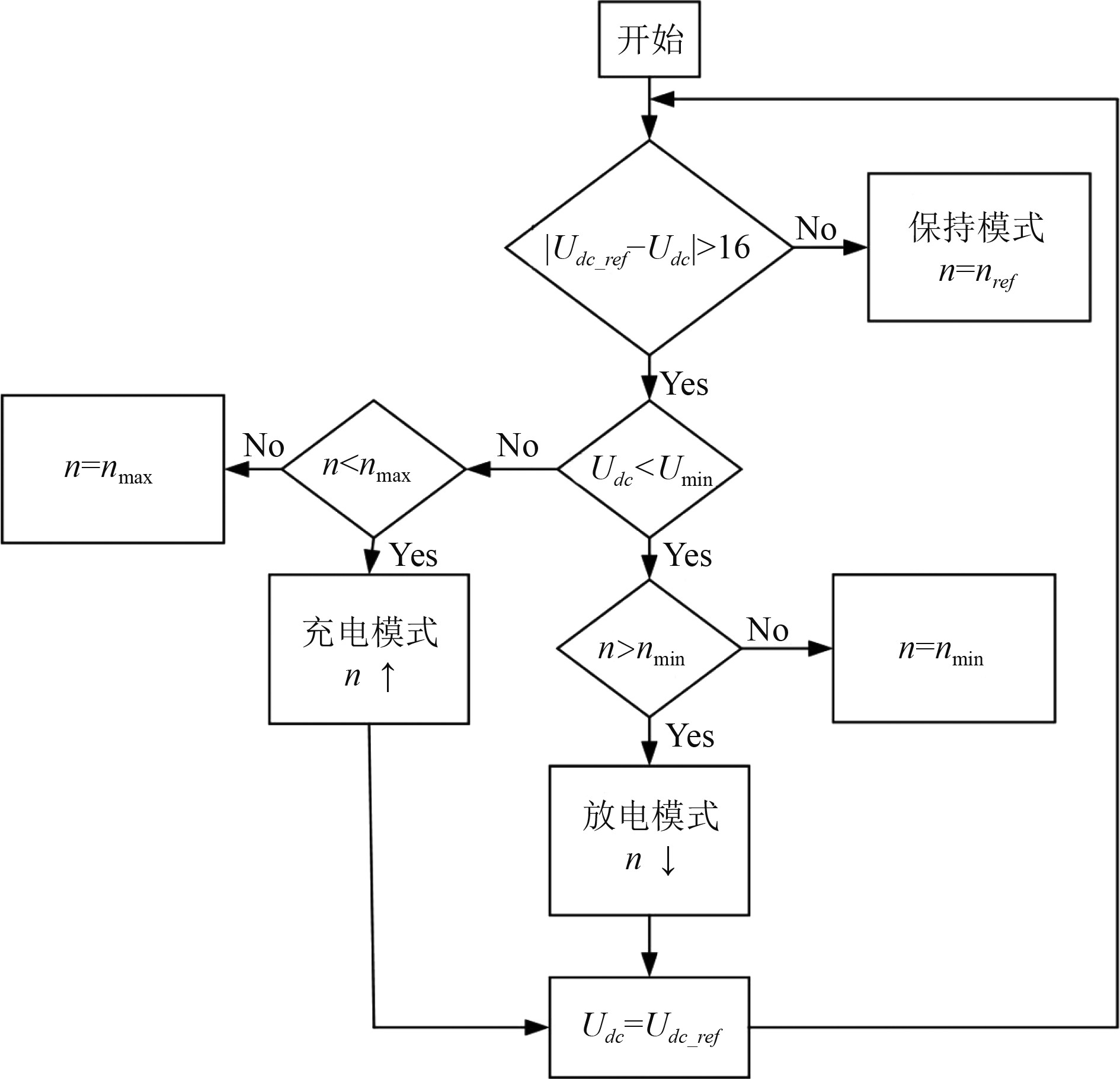
变流器必须具有控制能量双向流动的能力。在飞轮加速储能阶段,变流器当作逆变器使用,将直流母线的能量传输到飞轮。在飞轮减速释能阶段,变流器当作整流器使用,将飞轮的能量释放到直流母线上。如图5所示,一个三相全控桥拓扑结构变流器用于将飞轮电机连接到直流母线。FESS旨在快速响应系统的瞬变,因此,对于飞轮储能电机,应具有转速高、调速范围大、可输出较大的扭矩和功率、较低的空载损耗和较长的使用寿命等特点。选择永磁同步电机(PMSM)作为FESS电机,因为它功率密度大、效率高、低损耗低噪声、转速范围宽。可实现对船舶大功率负载频繁变化造成电压波动的大功率充放电补偿。
|
图 5 飞轮储能系统工作模式自动切换逻辑 Fig. 5 Automatic switching logic for the working mode of flywheel energy storage system |
在FESS中,飞轮转子与永磁同步电机连接在同一轴上,转速保持一致,通过对永磁同步电机进行控制,可实现FESS与直流微电网之间能量的双向流动。目前永磁同步电机的控制技术主要有矢量控制和直接转矩控制2种,相较于直接转矩控制,矢量控制调速范围比较宽。因此采用的是定子直轴零电流(
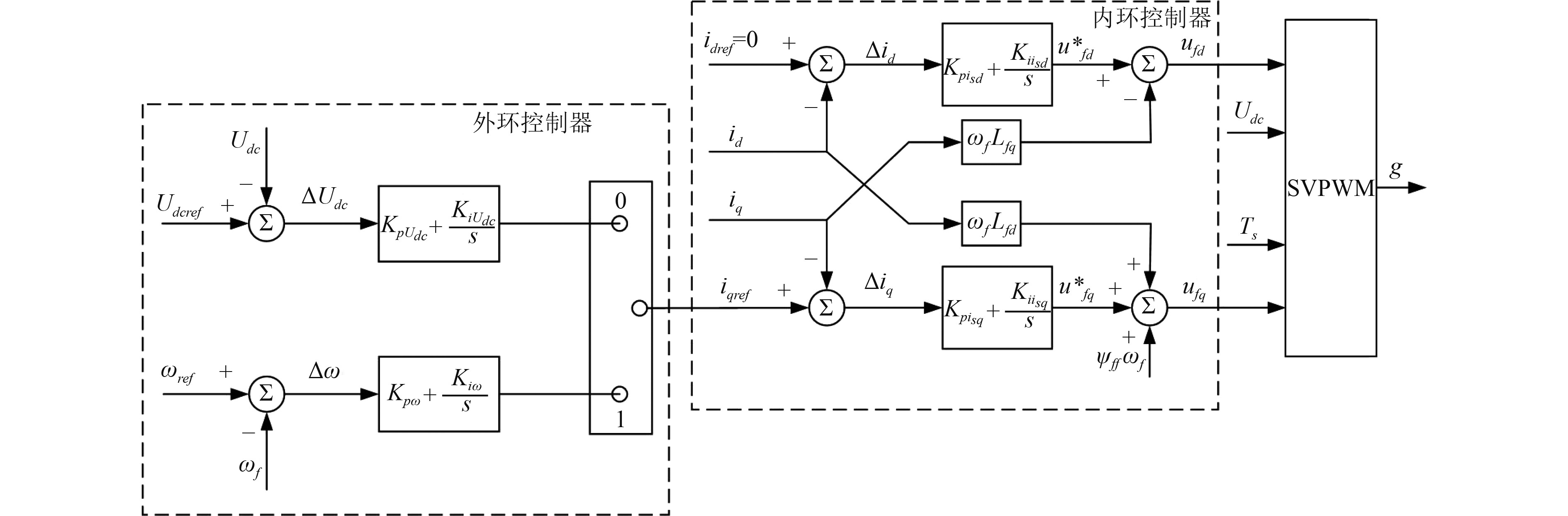
在启动阶段和保持阶段采用“转速外环+电流内环”的双环控制策略[15]。“外环控制器”控制电机转速
在调节阶段采用“电压外环+电流内环”的双环控制策略。此时,“外环控制器”改为控制直流母线侧电容电压
|
图 4 飞轮储能系统内环和外环控制器 Fig. 4 Inner and outer loop controllers of the flywheel energy storage system |
这2种控制方式的 “内环控制器”是相同的,它的结构与永磁同步电机在
假设永磁同步电机输出的三相电压为
| $ \left\{ \begin{gathered} {u_{fd}} = {R_{fs}}{i_{fd}} + \frac{{{\rm{d}}{\psi _{fd}}}}{{{\rm{d}}t}} - {\omega _f}{\psi _{fq}},\\ {u_{fq}} = {R_{fs}}{i_{fq}} + \frac{{{\rm{d}}{\psi _{fq}}}}{{{\rm{d}}t}} - {\omega _f}{\psi _{fd}}。\\ \end{gathered} \right. $ | (18) |
| $ \left\{ \begin{gathered} {\psi _{fd}} = {L_{fd}}{i_{fd}} + {\psi _f},\\ {\psi _{fq}} = {L_{fq}}{i_{fq}}。\\ \end{gathered} \right. $ | (19) |
式中:
将式(19)代入到式(18),可将电压方程进一步写成,
| $ \left\{ \begin{gathered} {u_{fd}} = {R_{fs}}{i_{fd}} + {L_{fd}}\frac{{{\rm{d}}{i_{fd}}}}{{{\rm{d}}t}} - {\omega _f}{L_{fq}}{i_{fq}} ,\\ {u_{fq}} = {R_{fs}}{i_{fq}} + {L_{fq}}\frac{{{\rm{d}}{i_{fq}}}}{{{\rm{d}}t}} + {\omega _f}{L_{fd}}{i_{fd}} + {\psi _{ff}}{\omega _f} 。\\ \end{gathered} \right. $ | (20) |
式中,
从上式可看出两电压分量仍存在耦合,不利于系统的控制,因此有必要进行定子电流前馈解耦,对式(20)中的电压进行前馈解耦补偿,采用工业成熟化的
| $ \left\{ \begin{gathered} u_{fd}^ * = {R_{fs}}{i_{fd}} + {L_{fd}}\frac{{{\rm{d}}{i_{fd}}}}{{{\rm{d}}t}} = \left( {{K_{dp}} + \frac{{{K_{di}}}}{S}} \right)\left( {i_d^ * - {i_d}} \right),\\ u_{fq}^ * = {R_{fs}}{i_{fq}} + {L_{fq}}\frac{{{\rm{d}}{i_{fq}}}}{{{\rm{d}}t}} = \left( {{K_{qp}} + \frac{{{K_{qi}}}}{S}} \right)\left( {i_q^ * - {i_q}} \right) 。\\ \end{gathered} \right. $ | (21) |
则式(20)变为:
| $ \left\{ \begin{gathered} {u_{fd}} = u_{fd}^ * - \Delta {u_{fd}} = u_{fd}^ * - {\omega _f}{L_{fq}}{i_{fq}} ,\\ {u_{fq}} = u_{fq}^ * - \Delta {u_{fq}} = u_{fq}^ * + {\omega _f}{L_{fd}}{i_{fd}} + {\psi _{ff}}{\omega _f} 。\\ \end{gathered} \right. $ | (22) |
从而可得出相对应的内环控制器如图4所示。电流内环的作用主要是对电流进行解耦。将电机输出的三相正弦电流,经过坐标变换后,即可得到实际的
对于MTGS,主电网采用直流供电,FESS通过并联的方式连接到直流母线上。FESS的自动切换逻辑设计如下:稳态情况下或者当电网电压波动不超过3%(16 V)的情况下,由同步发电机的励磁系统进行调节,FESS维持在保持模式。当系统投切大功率负载,导致电压的波动超过3%时,FESS及时响应系统的变化,切换到调节模式,与发电机励磁调节器协调工作,共同调节母线电压,防止母线电压波动过大。同时也要检测飞轮储能电机的转速,飞轮电机的转速不能超过设定的阈值。根据仿真实验,当飞轮转速降低至约1800
在MTGS中,由于微型燃气轮机发电机系统响应慢,大功率负载的投切会引起较大的电压暂降和直流母线电压过冲,造成系统的不稳定。FESS可补偿发电机和负载之间的功率不平衡,抑制电压波动,提高系统的稳定性。在Matlab/Simulink平台下搭建带有FESS的MTGS整体模型。
系统的主要参数如表1所示。
|
|
表 1 系统仿真主要参数 Tab.1 Main parameters of the simulation system |
额定的直流母线电压为513 V,如果实际电压的波动在3%以内,则认为可通过励磁系统去调节。如果超过3%,说明系统的扰动比较大,无法依靠励磁系统去调节,这时候就需将FESS切换到调节模式,以消除干扰并使直流电压回到给定的范围内。船舶直流电力系统直流母线电压波动幅值应在±10%之内[16]。为验证所提控制策略的可行性,同时对比分析了突加突卸40%(32
在此仿真模拟中,有接入FESS和不接入FESS两种模式。初始时,设定在直流母线中接入10
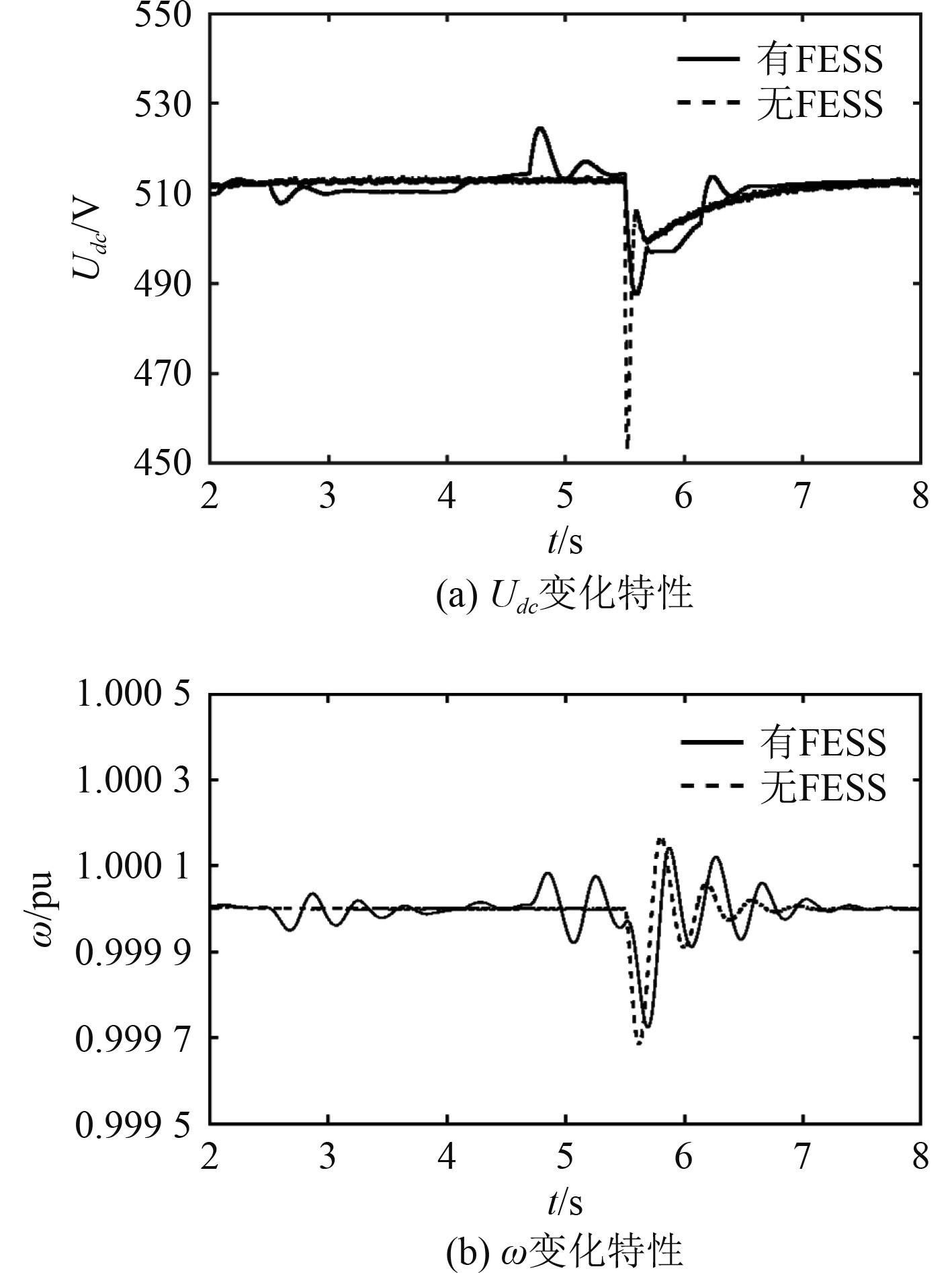
在接入FESS和不接入FESS的模式下,分别进行突加40%、60%、80%额定功率负载,母线电压
|
图 6
突加40%额定负载时
|
|
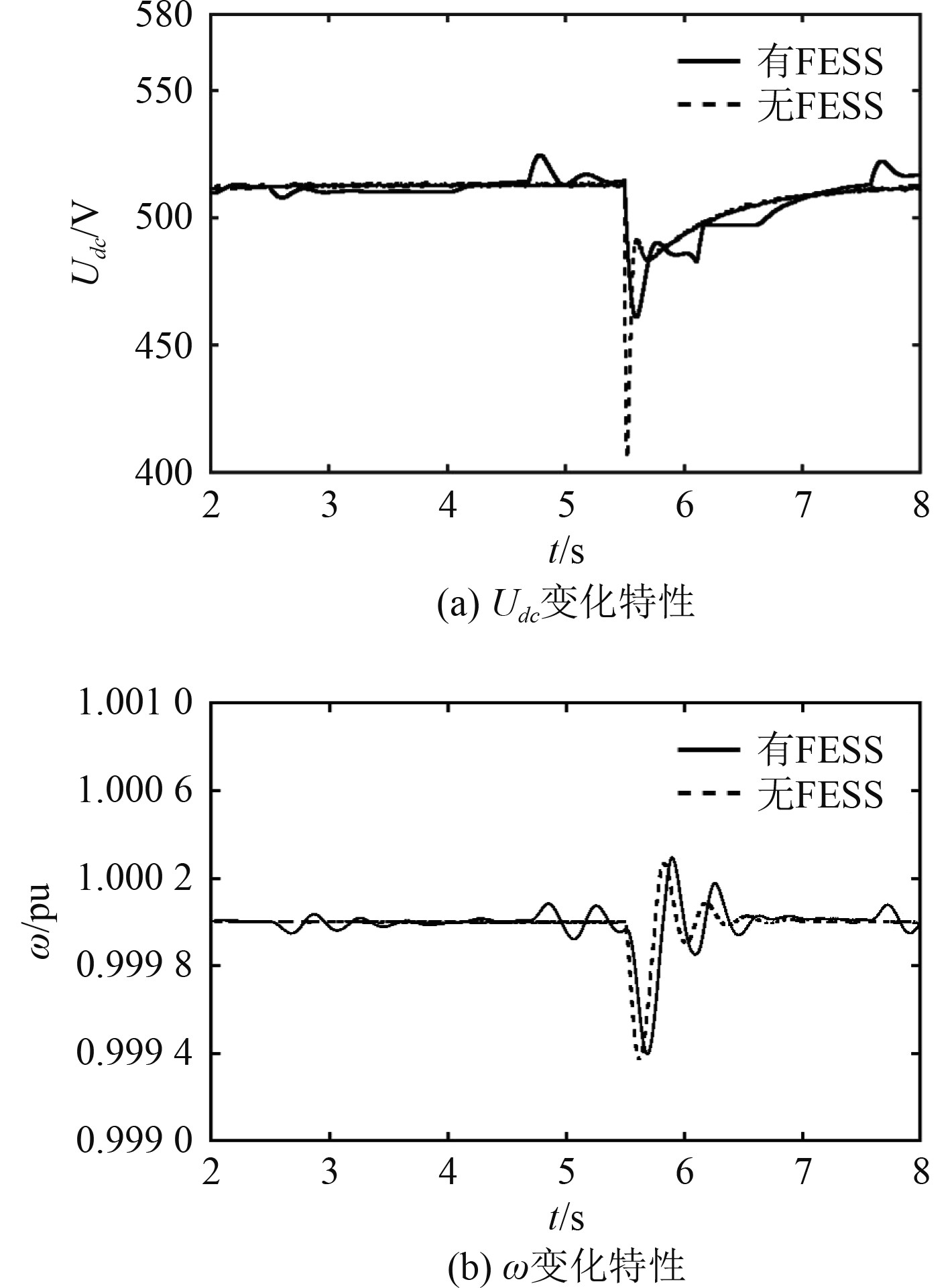
图 8
突加80%额定负载时
|
由图6可知,不接入FESS的模式下,5.5 s时突加40%额定负载,
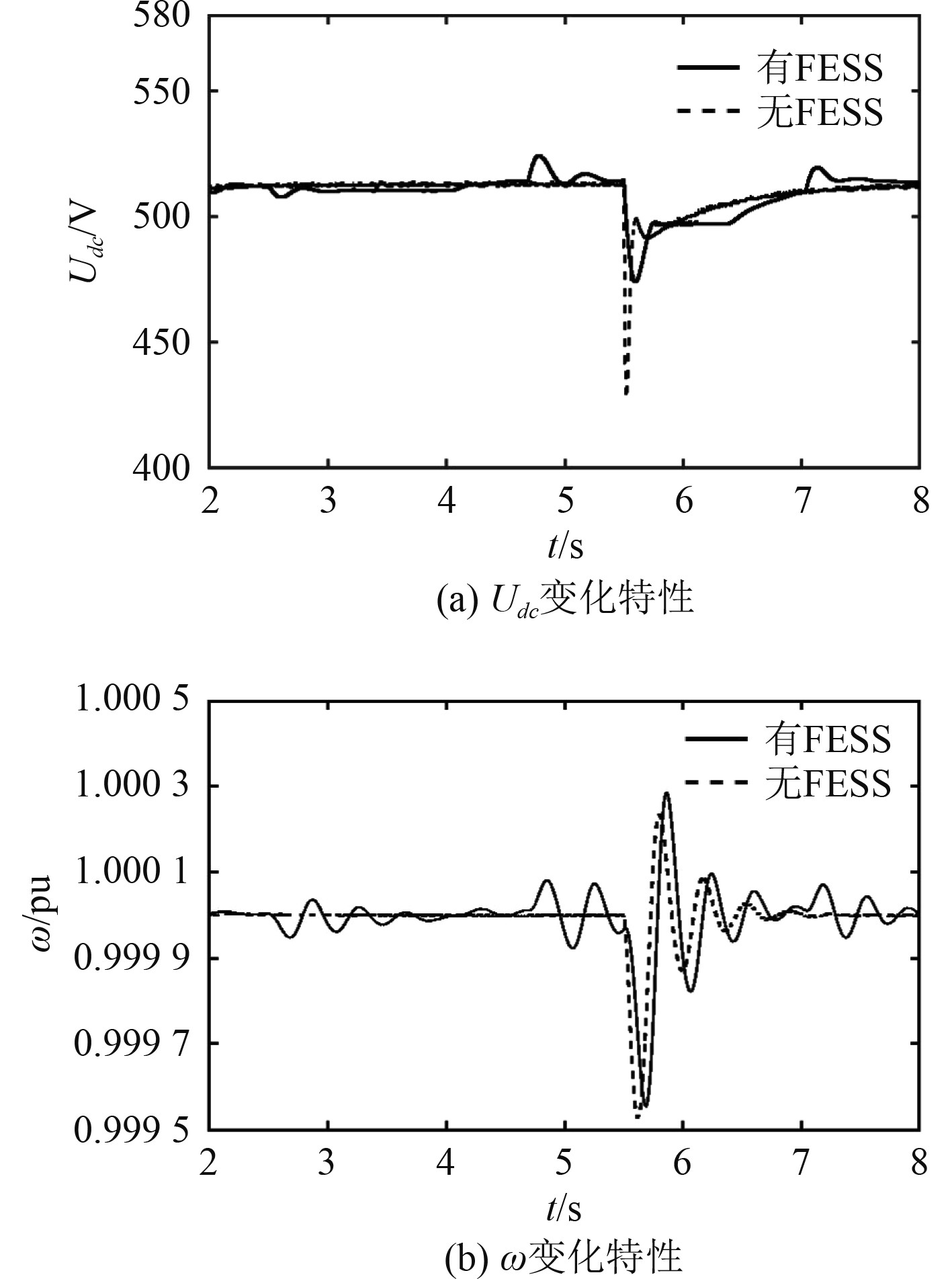
由图7可知,不接入FESS的模式下,5.5 s时突加60%额定负载,
|
图 7
突加60%额定负载时
|
由图8可知,不接入FESS的模式下,5.5 s时突加80%额定负载,
对比图6~图8可知,突增负载功率越大,造成的直流母线电压和同步发电机转速跌落越大,并且需要更多的时间恢复稳定。相比于突加40%额定负载,突加80%额定负载时,不接入FESS模式下,电压跌落量增加46.8 V,增加了9.1%,稳定时间增加了0.56 s。接入FESS模式下,电压跌落量增加25.5 V,增加了4.9%,稳定时间也多了0.47 s。甚至在不接入FESS情况下突加40%、60%和80%负载时,
|
|
表 2 突加不同功率负载时
|
|
|
表 3 突加不同功率负载时
|
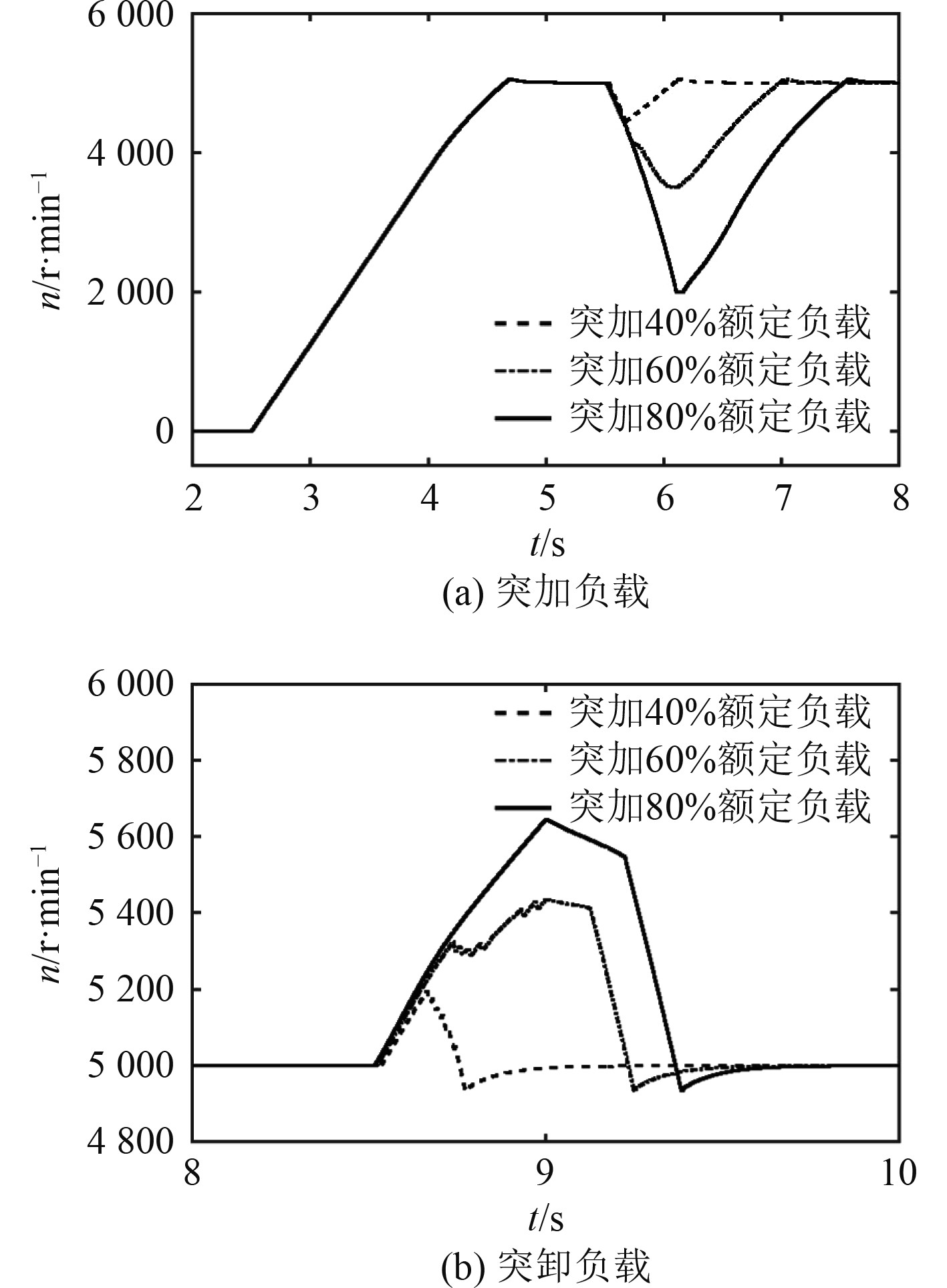
突增负载时飞轮转速变化特性见图9(a)。可知,MTGS突增负载的功率越大,FESS转速变化越大,也就是释放更多的能量来平抑母线电压的波动,突加80%负载时,飞轮转速的跌落最大,达到了飞轮的最低转速2 000
|
图 9
突加、突卸负载时飞轮转速
|
|
|
表 4 飞轮转速变化特性 Tab.4 Performance characteristics of flywheel speed |
在突加不同功率负载的基础上,进行突卸不同功率负载的仿真,母线电压
|
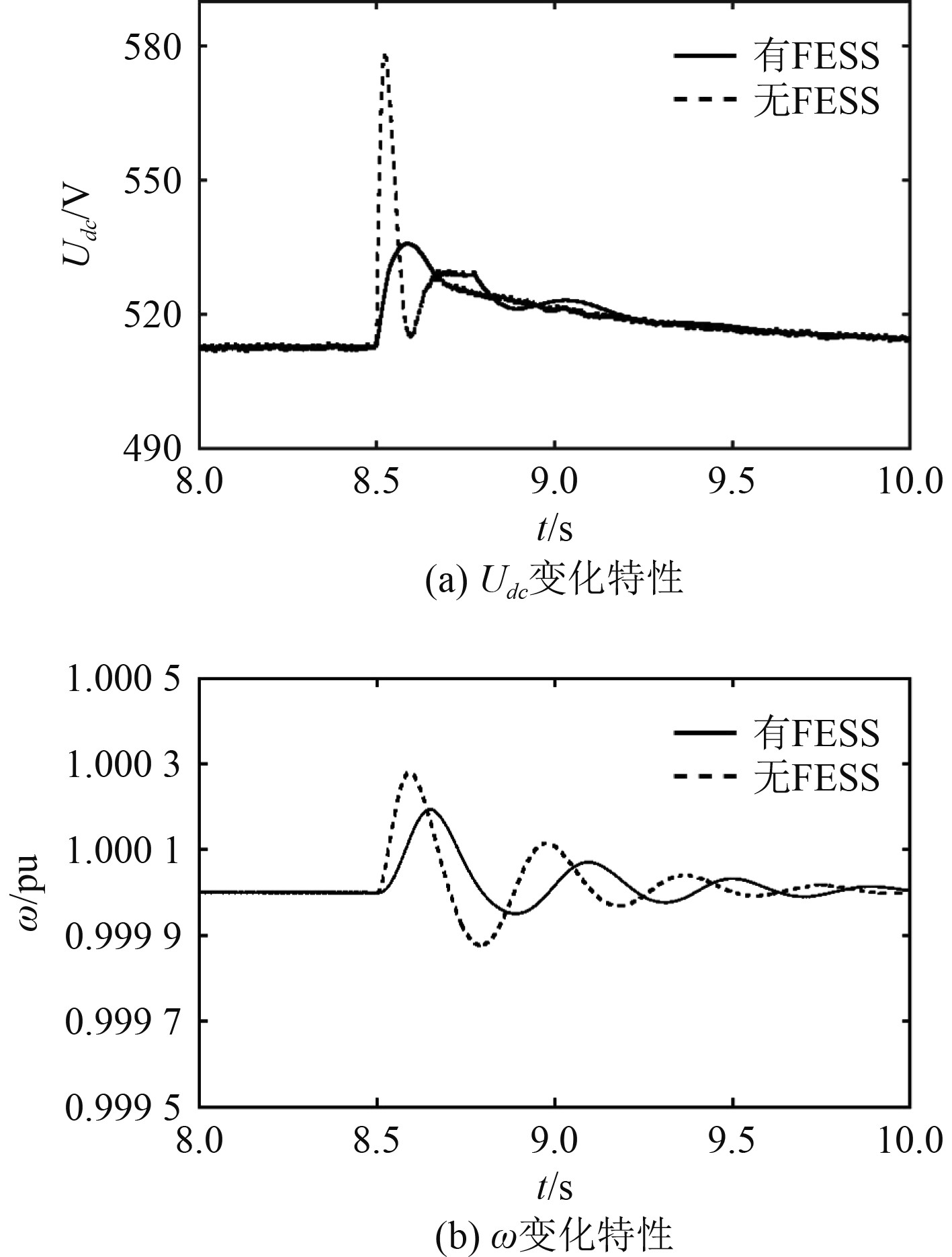
图 10
突卸40%额定负载时
|
|
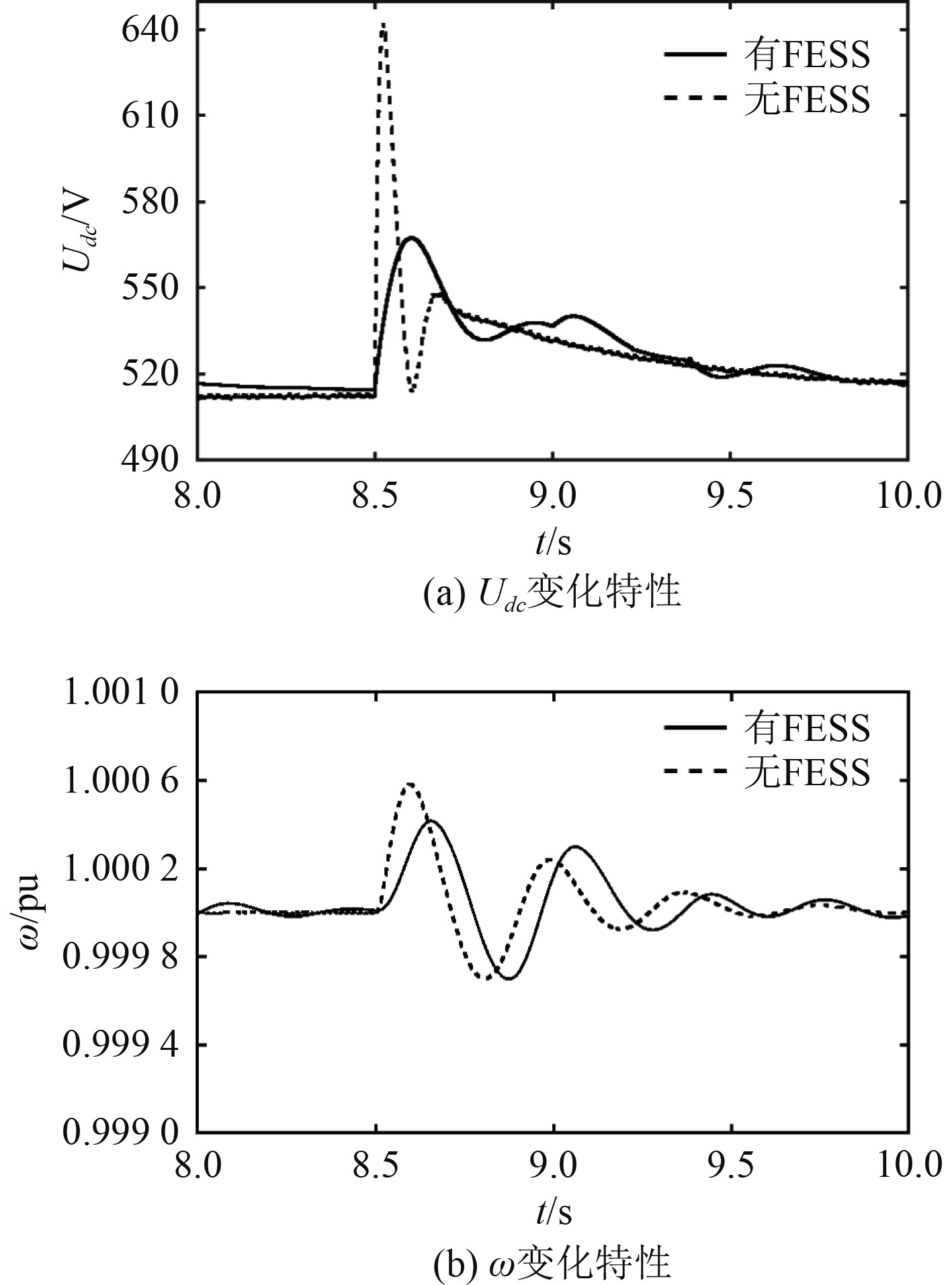
图 12
突卸80%额定负载时
|
由图10可知,不接入FESS的模式下,8.5 s时突卸40%额定负载,
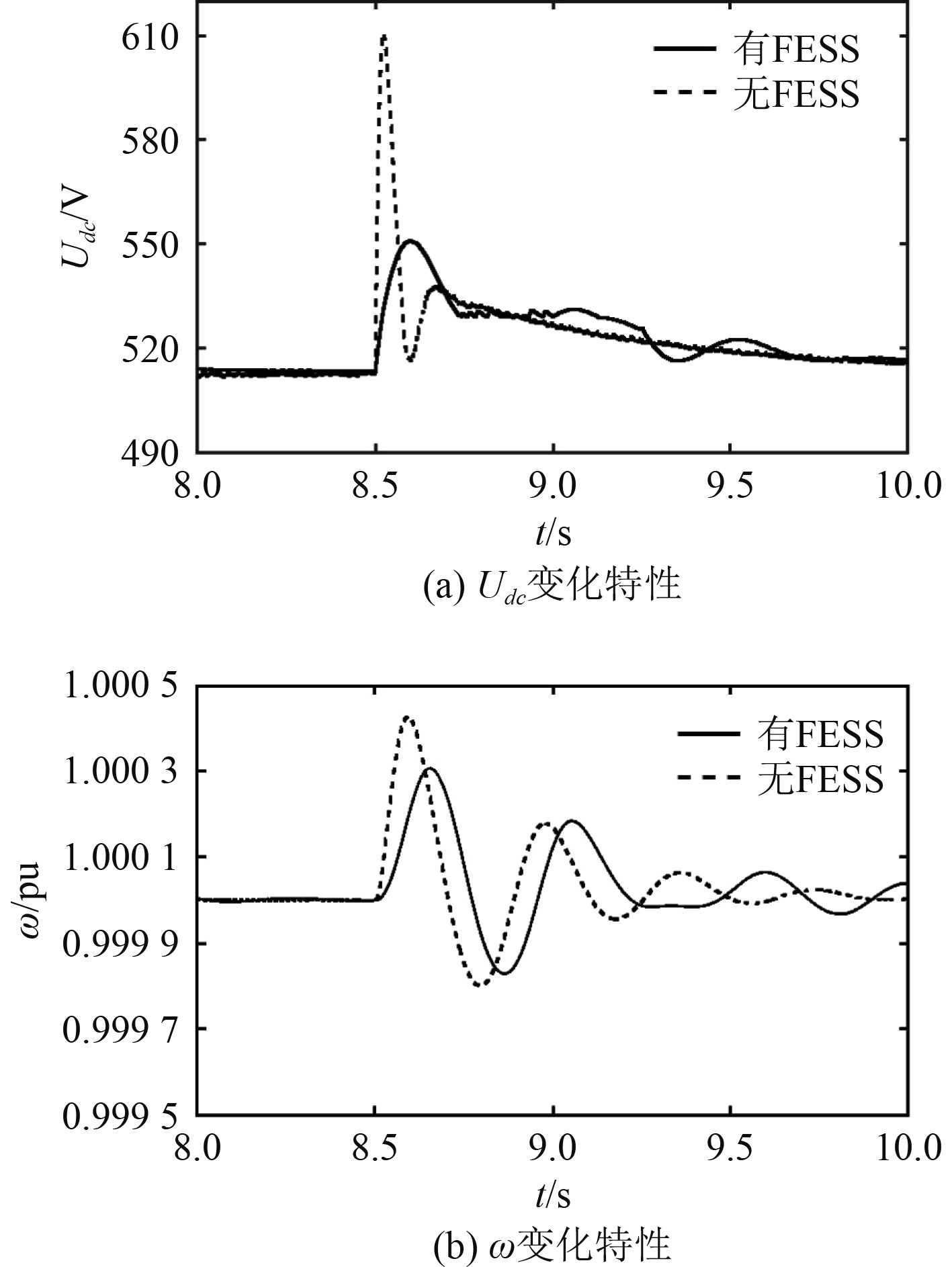
由图11可知,不接入FESS的模式下,8.5 s时突卸60%额定负载,
|
图 11
突卸60%额定负载时
|
由图12可知,不接入FESS的模式下,8.5 s时突卸80%额定负载,
对比图10~图12可知,突卸负载功率越大,造成的直流母线电压和同步发电机转速上升越大,并且需要更多的时间恢复稳定。相比于突卸40%额定负载,突卸80%额定负载时,不接入FESS模式下,电压上升量增加了64.4 V,增加12.4%,稳定时间也多了0.32 s。接入FESS模式下,电压上升量增加了31.7V,增加了6.2%,稳定时间也增加0.24 s。甚至在不接入FESS情况下突卸40%、60%和80%负载时,
|
|
表 5 突卸不同功率负载时
|
|
|
表 6 突卸不同功率负载时
|
突卸负载时飞轮转速变化特性见图9(b)。可知,MTGS突卸负载的功率越大,FESS转速变化越大,也就是吸收更多的能量来平抑母线电压的波动。飞轮转速的变化特性见表4。
4 结 语本文对微型燃气轮机、同步发电机励磁系统以及FESS进行理论分析,并建立了MTGS直流微电网完整的模型,设计了FESS的控制策略,并对突加突卸40%、60%、80%负载,不接入FESS和接入FESS两种情况下直流母线电压和同步发电机转速变化的特性进行了仿真分析。仿真结果表明,在MTGS直流母线上并联接入FESS可有效减少大功率负载的投切对直流母线电压的影响,维持母线电压在合理的范围内,提高直流微电网电能的品质。同时,可有效减少微型燃气轮机转速的瞬态变化曲率,避免产生较大的扭矩。
| [1] |
马伟明. 舰船综合电力系统中的机电能量转换技术[J]. 电气工程学报, 2015, 10(4): 3-10. DOI:10.11985/JEE.2015.04.003 |
| [2] |
FANG S, WANG Y, GOU B, et al. Toward future green maritime transportation: An overview of seaport microgrids and all-electric ships[J]. IEEE Transactions on Vehicular Technology, 2019, 69(1): 207-219. |
| [3] |
Li J, Liu F, Chen Y, et al. Resilience control of DC shipboard power systems[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6675-6685. DOI:10.1109/TPWRS.2018.2844161 |
| [4] |
Ali Z, Terriche Y, Hoang L Q N, et al. Fault management in DC microgrids: A review of challenges, countermeasures, and future research trends[J]. IEEE Access, 2021, 9(12): 128032-128054. |
| [5] |
DESSORNES O, LANDAIS S, VALLE R, et al. Advances in the development of a microturbine engine[J]. Journal of Engineering for Gas Turbines Power, 2014, 136(7): 071201. DOI:10.1115/1.4026541 |
| [6] |
SELJAK T, BUFFI M, VALERA-MEDINA A, et al. Bioliquids and their use in power generation-A technology review[J]. Renewable and Sustainable Energy Review, 2020, 129(10): 109930. |
| [7] |
DUAN J, LIU J, XIAO Q, et al. Cooperative controls of micro gas turbine and super capacitor hybrid power generation system for pulsed power load[J]. Energy, 2019, 169: 1242-1258. DOI:10.1016/j.energy.2018.12.004 |
| [8] |
HARDAN F, NORMAN R, TRICOLI P. Control and operation of a ship AC/DC microgrid under transient propulsion and manoeuvring load conditions[J]. International Journal of Electrical Power and Energy Systems, 2022, 139: 107823. DOI:10.1016/j.ijepes.2021.107823 |
| [9] |
DUAN J, FAN S, WU F, et al. Power balance control of micro gas turbine generation system based on supercapacitor energy storage[J]. Energy, 2017, 119: 442-452. DOI:10.1016/j.energy.2016.12.063 |
| [10] |
ZHOU Z, BENBOUZID M, CHARPENTIER, et al. A review of energy storage technologies for marine current energy systems[J]. Renewable and Sustainable Energy Reviews, 2013, 18: 390-400. DOI:10.1016/j.rser.2012.10.006 |
| [11] |
ARANI A A K, GHAREHPETIAN G B, ABEDI M. Review on energy storage systems control methods in microgrids[J]. International Journal of Electrical Power and Energy Systems, 2019, 107: 745-757. DOI:10.1016/j.ijepes.2018.12.040 |
| [12] |
王松岑, 来小康, 程时杰. 大规模储能技术在电力系统中的应用前景分析[J]. 电力系统自动化, 2013, 37(1): 3-8. |
| [13] |
戴兴建, 姜新建, 张剀. 飞轮储能系统技术与工程应用 [M]. 北京: 化学工业出版社, 2021.
|
| [14] |
FADDEL S, SAAD A A, HARIRI M E, et al. Coordination of hybrid energy storage for ship power systems with pulsed loads [J]. IEEE Transactions on Industry Applications, 2020, 56(2): 1136-1145.
|
| [15] |
SALEH A, AWAD A, GHANEM W. Modeling, control, and simulation of a new topology of flywheel energy storage systems in microgrids[J]. IEEE Access, 2019, 7: 160363-160376. DOI:10.1109/ACCESS.2019.2951029 |
| [16] |
刘永葆, 文强, 贺星, 等. 飞轮储能对船用燃气轮机发电系统稳定性影响的仿真研究[J]. 海军工程大学学报, 2017, 29(6): 60-66. |
| [17] |
邱子鉴, 李宝国, 郑怡璇. 光伏微电网储能平抑功率波动的控制策略研究[J]. 辽宁工业大学学报, 2021, 41(5): 312-316. |
| [18] |
支娜, 丁有国, 赵佳宝. 直流微电网改进虚拟直流电机控制策略[J]. 电力电子技术, 2020, 54(12): 93-95. |
| [19] |
梁明玉, 蔡新红, 龚立娇, 等. 基于下垂控制的微电网并网预同步控制研究[J]. 计算机仿真, 2022, 39(4): 80-86. |
| [20] |
李浩冬, 刘永葆, 贺星. 微型燃气轮机动态特性仿真[J]. 舰船科学技术, 2020, 42(21): 91-95. DOI:10.3404/j.issn.1672-7649.2020.11.018 |
| [21] |
翟小飞, 刘德志, 欧阳斌, 等. 双闭环控制的三相整流发电机数字式励磁系统[J]. 电机与控制学报, 2011, 15(3): 19-24. |
| [22] |
邵梦麟, 梁前超, 闫东, 等. 船用燃气轮机发电机组动态性能仿真[J]. 舰船科学技术, 2016, 38(7): 71-76. DOI:10.3404/j.issn.1672-7619.2016.07.016 |
 2023, Vol. 45
2023, Vol. 45

