2. 武汉理工大学 自动化学院,湖北 武汉 430000
2. Wuhan University of Technology, Wuhan 430000, China
随着“双碳”目标的提出,我国全电力推进船舶的研究发展极为迅速,其中全电力推进船舶的负荷预测成为热点问题。由于船舶水上作业的特殊性,为保证其功能运行的可靠性和经济性,全电力推进船舶负荷预测的准确性显得尤为重要。
全电力推进船舶作业时的复杂工况导致其电力系统负荷具有很强的随机性,无法找到精确的数学模型刻画[1]。目前针对电力推进船舶负荷预测多用人工神经网络方法,包括BP、RBF、Elman等[2-4],也有采用SVM模型对短期负荷进行预测[5-6]。上述研究多为一般工况下的负荷预测,而针对全电力推进船舶在复杂恶劣工况下的短期负荷预测少有涉及。
本文针对在复杂恶劣工况下的全电力推进船舶负荷特点,采取RBF神经网络算法对短期负荷情况进行预测。综合考虑水流速度、吃水深度、载重量、电力负荷4个维度,提高了短期负荷预测的准确性。
1 全电力推进船舶负荷特点分析全电力推进船舶是指采用电力推进技术,用以变频器和推进电机为核心组成的新型动力系统代替以柴油机和机械转动装置为核心的传统动力系统的船舶,船舶正常运行的全部动力都来自于船舶电力系统所提供的电力[7]。由于船舶水上作业时存在多种工况,包括巡航、加减速、倒车制动等,各种工况所对应的推进电机的功率有很大差别,导致全电力推进船舶的负荷波动很大。
按照负荷情况分类,全电力推进船舶的负荷总体上可分为2大类,一类是功率波动很小的负荷,包括日常生活所需负荷、通信负荷和照明负荷等;另一类是功率波动较大的负荷,主要是推进电机为主的动力系统负荷。此负荷特性使得船舶运行时的电力系统负荷具有连续性的特点[8]。
基于全电力推进船舶负荷的大波动性和连续性,本文选择RBF神经网络算法进行短期负荷预测。相较于BP、Elman等网络结构,RBF神经网络的结构简单、收敛速度快、预测误差小,能够逼近任何非线性函数,很大程度上避免因负荷波动过大而导致的预测网络不收敛的情况。同时,RBF网络有很好的全局逼近能力,可解决BP等网络可能出现的陷入局部最优解的问题。因此对于全电力推进船舶短期负荷预测问题,RBF神经网络结构预测结果更加可靠。
2 基于RBF神经网络预测的基本原理基于RBF神经网络预测的基本思想为:用RBF神经元构成的隐藏层空间对输入变量进行空间变换,将低维空间内非线性不可分的数据变换为高维空间内线性可分数据。所谓预测,本质上为拟合多维非线性函数求解对应函数值的过程。
图1为RBF神经元模型结构图。其中
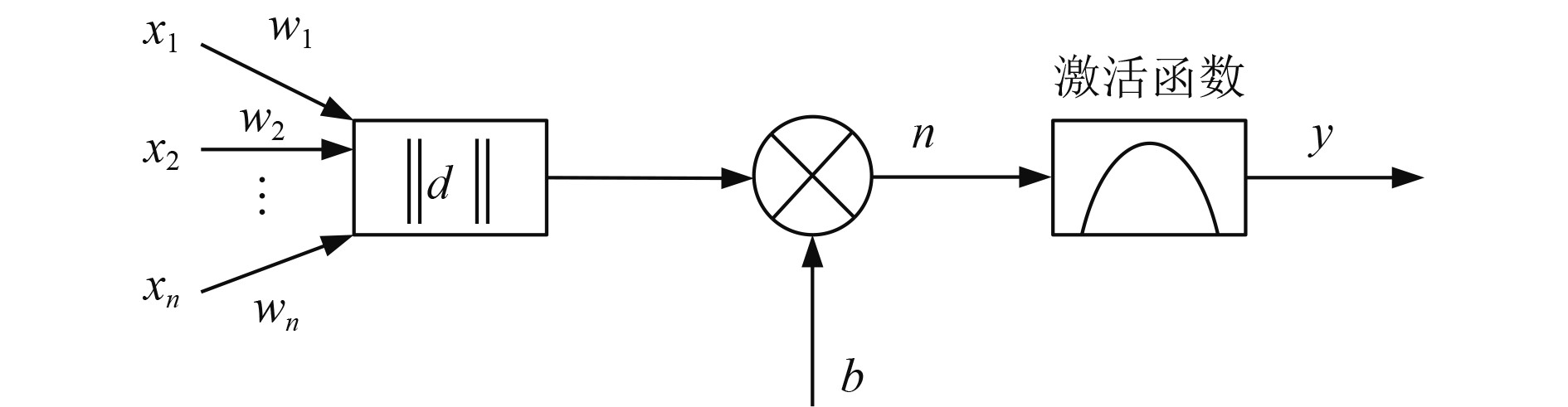
|
图 1 RBF神经元模型结构 Fig. 1 RBF Neuron model structure |
由图1可知,由输入向量
| $ F\left( {\left\| {{d}} \right\|} \right){\text{ = }}{e^{ - {n^2}}}。$ | (1) |
随着自变量
RBF神经网络是单隐层的3层静态前向网络,结构如图2所示。第1层为输入层,此层不做任何变换,仅传递输入的数据信息;第2层为隐含层,具体隐含层神经元个数根据实际预测情况而定,此层对输入的数据信息做空映射的变换,采用非线性优化策略对激活函数参数进行调整;第3层为输出层,此层对隐含层神经元输出的数据信息通过线性加权后作为整个网络的输出结果[10]。
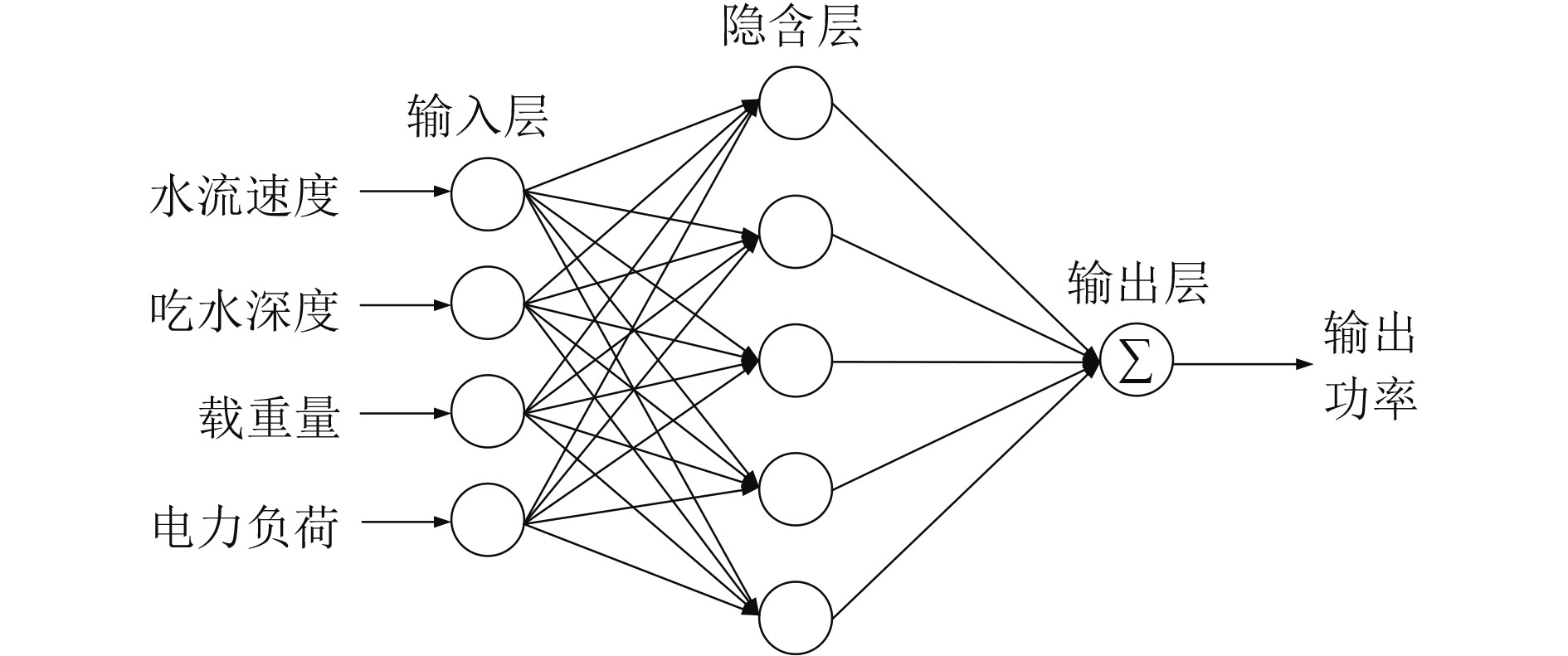
|
图 2 RBF神经网络结构 Fig. 2 Structure of RBF neural network |
全电力推进船舶的实际运行数据不能直接当作RBF神经网络的输入进行负荷预测,要对运行数据从历史数据选取和归一化两方面进行预处理,以防止收敛网络发散和神经元饱和的问题。
3.1.1 历史数据选取选取船舶实际运行的历史数据作为样本输入至RBF神经网络中训练要综合样本数量和样本大小两方面考虑。显然,大量的训练样本可以提高网络的拟合效果从而增加预测的准确性,但是如果训练样本过多会使得训练时间太长,出现网络过拟合问题;训练样本太少会导致预测网络不完善,甚至出现预测网络发散的情况。因此,本文选取训练集和测试集比例为5∶1。
由于全电力推进船舶运行时工作状态的不确定性,在某些时刻船舶的电力负荷可能出现极大或极小的情况,这会导致预测网络无法收敛,预测结果发散,此类异常数据不可加入样本集实施预测。一般来说,船舶的电力系统负荷在前后一两个时刻内不会有太大差别。因此,对此类极端情况设置最大临界值和最小临界值,即
| $ {P_{\min }} \leqslant {P_{sel}} \leqslant {P_{\max }}。$ | (2) |
式中:
当船舶实际运行时的负荷值满足式(2)时,直接可以取做预测样本;当其负荷值超过此范围时,取最大或最小临界值当做预测样本。
3.1.2 归一化处理将输入数据通过简化计算,变换到一定范围之内,此过程称为归一化。归一化处理可加快网络收敛速度,提高预测精度,关键是避免出现神经元饱和的问题。本文采用缩放法实施归一化处理,公式如下:
| $ G = \frac{{{G_0} - {G_{\min }}}}{{{G_{\max }} - {G_{\min }}}}。$ | (3) |
式中:
将船舶实际运行时的水流速度、吃水深度、载重量、电力负荷数据代入式(3)进行归一化处理再输入至RBF神经网络中,将预测数据再实施反归一化处理,得到的原始数值作为最终的预测结果。对应反归一化公式如下:
| $ {G_0} = \left( {{G_{\max }} - {G_{\min }}} \right)G + {G_{\min }} 。$ | (4) |
构建基于RBF神经网络全电力推进船舶负荷预测模型首先要确定输入输出变量维数,选择水流速度、吃水深度、载重量、电力负荷四维变量输入,对应的输出变量定义为船舶单次航程的短期负荷预测结果,其具体表达式为:
| $ y\left( t \right) = \varphi \left[ {v\left( t \right),h\left( t \right),w\left( t \right),x\left( {t - 1} \right), \cdots ,x\left( {t - \delta } \right)} \right]。$ | (5) |
式中:
预测步骤如图3所示。将所选数据输入,判断是否为异常数据;若是则返回重新选择,若不是则进行归一化处理;归一化后的四维样本输入至RBF预测模型中,模型输出结果反归一化后作为最终负荷预测结果。
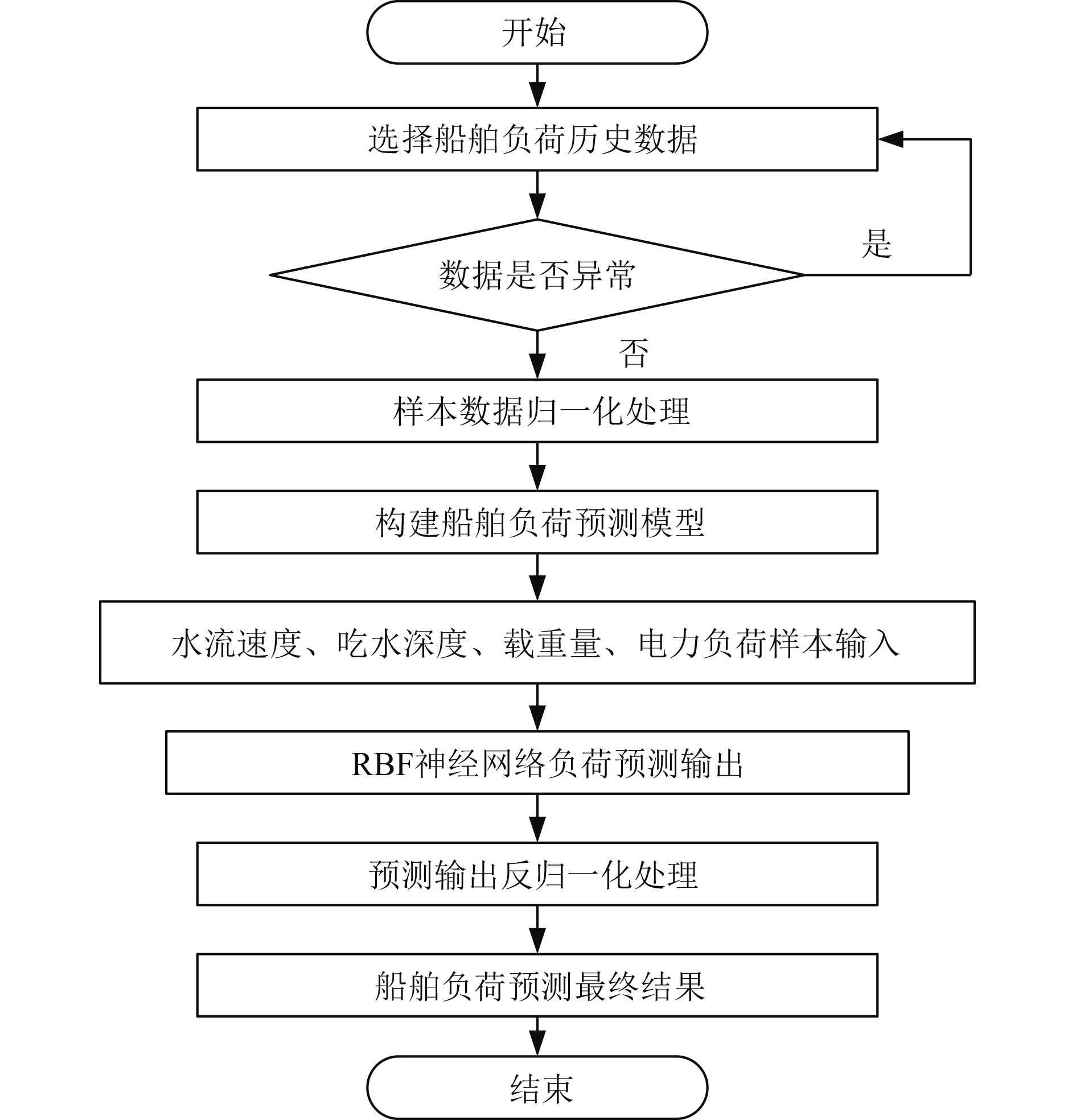
|
图 3 RBF神经网络预测流程图 Fig. 3 RBF Neural Network prediction flowchart |
确定上海某公司研发的全电力推动船舶为研究对象,对其在湍急水流的恶劣环境下复杂工况进行短期负荷预测。分别选取空载、轻载、重载和满载下船舶具有代表性的工况为预测样本,如停泊、启航、巡航、加减速、二次加速、倒车制动等。
4.1 仿真模型参数由于预测模型采用水流速度、吃水深度、载重量、电力负荷四维输入,负荷预测结果一维输出;故对应的输入层神经元数为4,输出层神经元数为1。而对于隐藏层神经元数,一般采用经验公式和试凑法相结合来确定,经验公式如下:
| $ N = \sqrt {X + Y} + M。$ | (6) |
式中:
通过该方法确定隐藏层神经元数为9,设定隐含层—输出层的权值、节点基宽、基函数中心的学习率分别为0.090、0.015、0.015,最大迭代次数为20000,误差精度要求为1E-4,其他参数均为默认值。具体参数设置如表1所示。
|
|
表 1 预测模型参数 Tab.1 Predicting model parameters |
在Matlab仿真环境中对全电力推进船舶在水流速度为2 km/h、吃水深度为2.7 m、载重量为800 t的情况下,进行单次航行的电力系统负荷预测。仿真结果与实际航行负荷值相对比表明,预测准确率达到93.4%,但出现个别时间点差异值过大问题,特别是初始值预测误差过大。
通过分析,训练样本中有一组航行数据在试航过程中存在浅水效应问题。由于试航地点京杭运河航道常年水位较浅,全年水深约3~5 m,此组训练样本试航时,水深约4.1 m,船舶吃水深度3.1 m,螺旋桨工作时距离河底小于1 m,此时浅水效应十分明显,对螺旋桨产生极大阻力,阻力值可达到长江航道等深水航道的3倍以上,极大影响船舶航行速度,导致船舶电力系统负荷出现异常值,进而使得个别时间点预测偏差过大。
对训练样本进行优化,去除异常训练样本再次进行负荷预测仿真,仿真预测效果对比如图4所示。从对比图看出,优化样本后的仿真效果明显高于优化前,预测准确率高达96.4%,基本可以完全拟合实际负荷值。
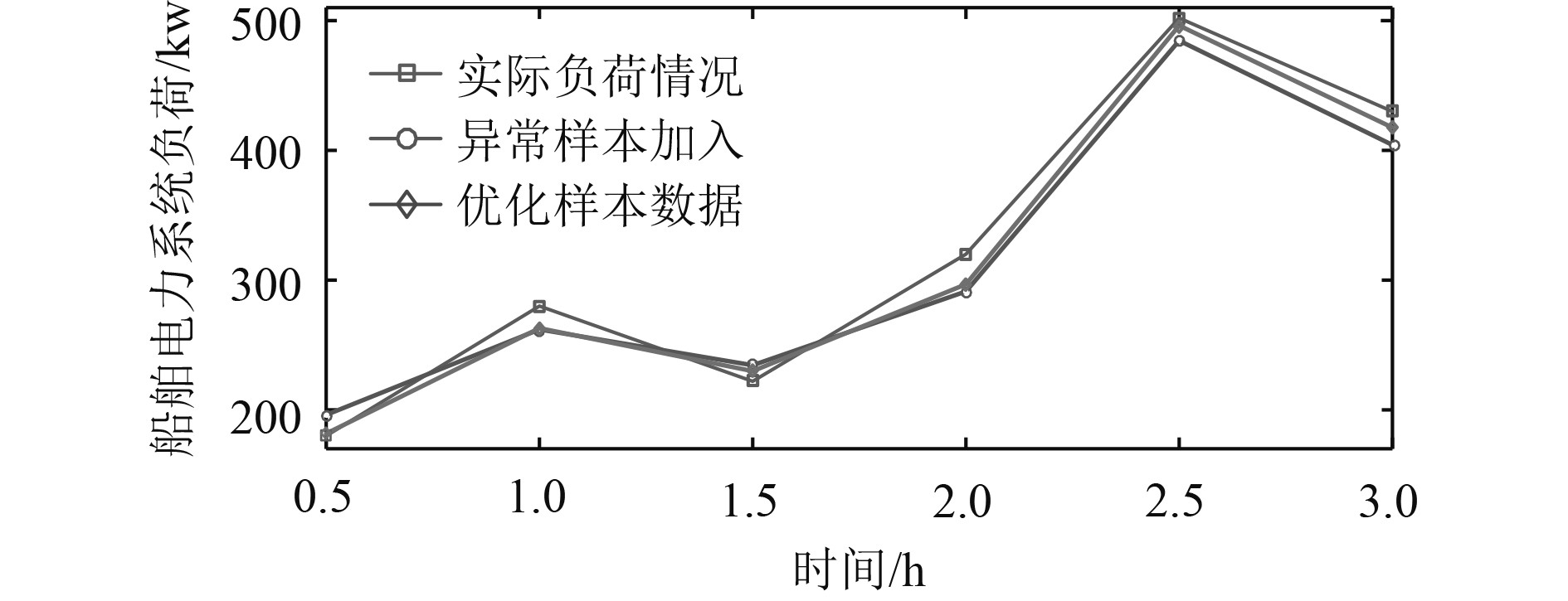
|
图 4 负荷预测效果对比 Fig. 4 Comparison of load forecasting effect |
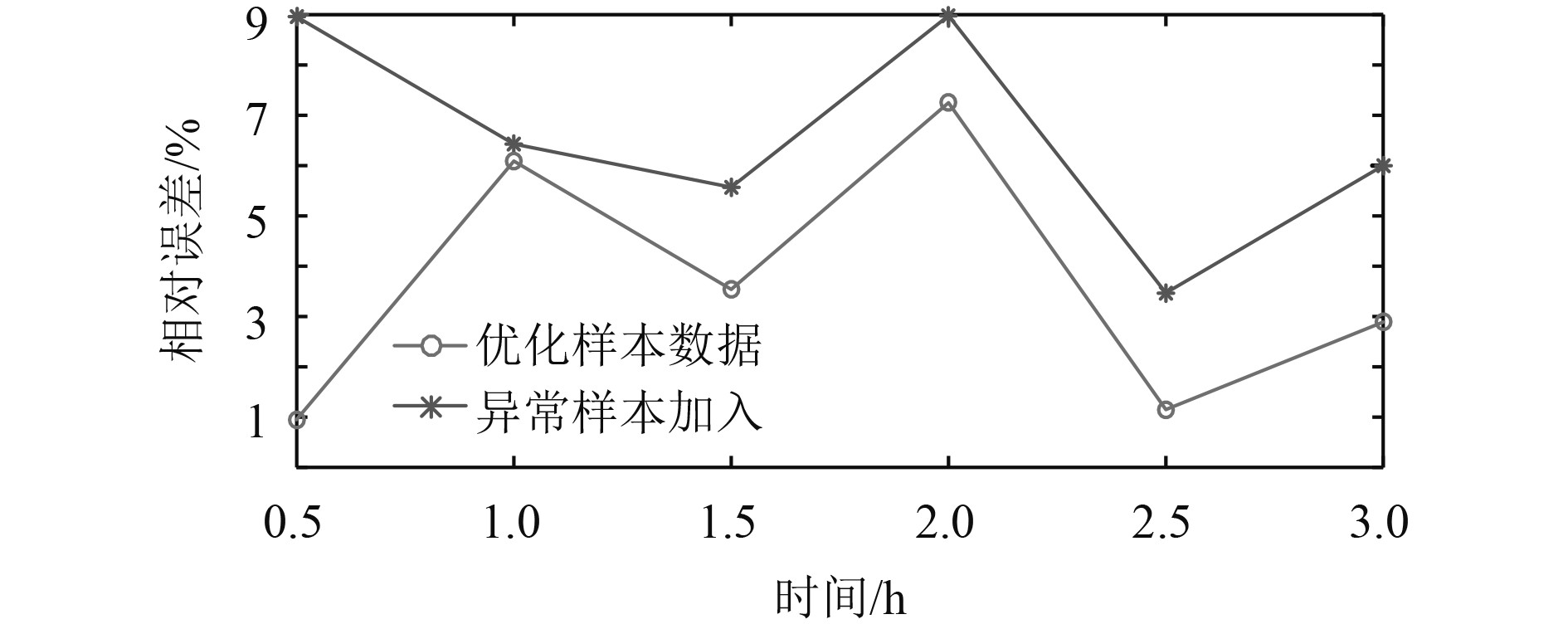
根据图4预测结果计算对应预测点的相对误差,结果如图5所示。可知,样本优化后各时间点相对误差大大减小并且初始值误差过大问题得以解决。
|
图 5 预测结果相对误差 Fig. 5 Relative error of prediction results |
对于神经网络预测来说,衡量网络预测效果一般采取3种评价指标:平均相对误差、均方根误差和决定系数。其对应公式如下:
平均相对误差
| $ {e_{MAP}} = \left( {\frac{1}{{n}}} \right) \times \sum\limits_{{{i = 1}}}^{{n}} {\left( {\frac{{\left| {{{{x}}_{{i}}} - {{{y}}_{{i}}}} \right|}}{{{{{y}}_{{i}}}}}} \right)} \times 100{\text{% }} ,$ | (7) |
均方根误差
| $ {e_{RMS}}= \sqrt {\left( {\frac{1}{{{n}}}} \right) \times \sum\limits_{{{i = 1}}}^{{n}} {{{\left( {{{{x}}_{{i}}} - {{{y}}_{{i}}}} \right)}^2}} },$ | (8) |
决定系数
| $ {R^2}{\text{ = }}\frac{{{{\displaystyle\sum\limits_{i = 1}^n {\left( {{x_i} - \overline y } \right)^2} }}}}{{{{\displaystyle\sum\limits_{i = 1}^n {\left( {{y_i} - \overline y } \right)^2} }}}} 。$ | (9) |
式中:
计算网络预测效果各评价指标如表2所示。
|
|
表 2 预测效果评价指标 Tab.2 Evaluation Index of prediction effect |
可知,优化样本数据后预测效果的各项评价指标均优于异常样本加入时的情况。优化后的决定系数高达0.945,说明模型拟合度很好,基于RBF神经网络进行负荷预测的效果显著。
5 结 语本文首先分析了复杂工况下全电力推进船舶的负荷特点,然后基于RBF神经网络的原理构建了全电力推进船舶的负荷预测模型,提出一种完整的负荷预测方法,最后在Matlab/Simulink中对船舶实际运行的负荷情况进行短期预测,预测精度高达96.4%,决定系数高达0.945,很好提高了模型拟合程度,实现了复杂工况下全电力推进船舶综合电力系统负荷的短期精准预测。
| [1] |
张宇涵, 高海波, 商蕾, 等. 基于神经网络模型的船舶电网短期电力负荷预测[J]. 应用科技, 2021, 48(5): 12-15+22. ZHANG Yuhan, GAO Haibo, SHANG Lei, et al. Short-term load forecasting for marine electric network based on neural network models[J]. Applied Science and Technology, 2021, 48(5): 12-15+22. DOI:10.11991/yykj.202101010 |
| [2] |
刘银波, 吕越. RBF神经网络在船舶电力负荷预测中的应用[J]. 舰船科学技术, 2021, 43(18): 121-123. LIU Yin-Bo, LV Yue. Application of RBF neural network in ship power load forecasting[J]. Ship Science And Techology, 2021, 43(18): 121-123. DOI:10.3404/j.issn.1672-7649.2021.9A.041 |
| [3] |
周旭, 来庭煜, 饶佳黎. 基于RBF神经网络模型的电力系统短期负荷预测[J]. 通信电源技术, 2018, 35(11): 152-154. ZHOU Xu, LAI Ting-yu, RAO Jia-li. Short term load forecasting of power system based on RBF neural network model[J]. Telecom Power Technology, 2018, 35(11): 152-154. DOI:10.19399/j.cnki.tpt.2018.11.057 |
| [4] |
宋明达. 基于改进遗传算法优化Elman神经网络的短期负荷预测[D]. 衡阳: 南华大学, 2020.
|
| [5] |
侯文君, 汪英英, 姚艺新, 等. 支持向量机的船舶短期电力负荷预测方法[J]. 舰船科学技术, 2018, 40(18): 79-81. HOU Wen-jun, WANG Ying-ying, YAO Yi-xin, et al. Short term load forecasting method based on support vector machine[J]. Ship Science and Techology, 2018, 40(18): 79-81. |
| [6] |
赵登福, 王蒙, 张讲社, 等. 基于支撑向量机方法的短期负荷预测[J]. 中国电机工程学报, 2002(4): 27-31. ZHAO Deng-fu, WANG Meng, ZHANG Jiang-she, et al. A support vector machine approach for short term load forecasting[J]. Proceedings of the CSEE, 2002(4): 27-31. DOI:10.3321/j.issn:0258-8013.2002.04.005 |
| [7] |
王嘉钰. 全电力推进船舶短期电力负荷预测研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [8] |
刘静. 最小二乘SVM在电力推进船舶电力负荷短期预测的应用[J]. 舰船科学技术, 2021, 43(24): 61-63. LIU Jing. Application of least square SVM in short-term forecasting of electric load of electric propulsion ship[J]. Ship Science and Technology, 2021, 43(24): 61-63. DOI:10.3404/j.issn.16727649.2021.12A.021 |
| [9] |
朱诗卉, 代焕利, 王飒, 等. RBF神经网络电力负荷预测模型研究[J]. 三峡大学学报(自然科学版), 2013, 35(5): 46-49. Zhu Shihui, Dai Huanli, Wang Sa, et al. Research on RBF neural network models of power load forecasting[J]. Journal of China Three Gorges Univercity (Natural Sciences), 2013, 35(5): 46-49. |
| [10] |
王成, 代祥, 刘飞, 等. 基于RBF神经网络的电力系统负荷预测[J]. 电力学报, 2018, 33(5): 399-407. WANG Cheng, DAI Xiang, LIU Fei, et al. Power system load forecasting based on RBF neural network[J]. Journal of Electric Power, 2018, 33(5): 399-407. DOI:10.13357/j.cnki.jep.002747 |
 2023, Vol. 45
2023, Vol. 45
