2. 河南工业大学 电气工程学院,河南 郑州 450001;
3. 中国科学技术大学 信息科学技术学院,安徽 合肥 230026
2. College of Electrical Engineering,Henan University of Technology, Zhengzhou 450001, China;
3. School of Information Science and Technology,University of Science and Technology of China, Hefei 230026, China
在传统船用动力系统的改造设计中,民用船舶多是从柴油机动力装置入手,按照船舶的航行速度可分为低速、中速及高速3种。而军用舰船,则多是从蒸汽动力装置及核动力装置进行设计,并且在检测系统上也存在一定的复杂性[1 – 3]。随着科学技术的发展,船用电控二冲程柴油机在节能、环保、自动化水准等方面取得了长足的进步,同时结构及零部件的复杂多样性,也让其动力系统的可靠性检测成为了当前一个亟需深入探讨的课题。船舶电控二冲程柴油机在工作原理上,由于船舶电控二冲程柴油机系统的复杂性及其在机械、电子、液压等领域的广泛应用,使得船用电控二冲程柴油机的故障诊断非常困难。目前的故障检修技术仅限于柴油机部件或子系统,难以在实践中快速、无误地判断故障的源头。
而小波神经网络模型在20世纪80年代逐渐得到应用,并且在运用上实现了迅速发展,其原理是通过人为模拟出数量众多的简单神经元,以某种方式联系起来,这是人工智能算法在STLF上的一个重要应用。目前,随着船舶行业正如火如荼的进行产业升级,也开始将小波神经网络引入船舶领域,其中包括硬件改造、软件升级、数字监控、模型预测等方向,并很好地提升了船舶系统的相关使用效率及性能[4 – 6]。
WNN模型结构如图1所示,其中的小波基函数就是一种基于小波分析理论的数学模型。
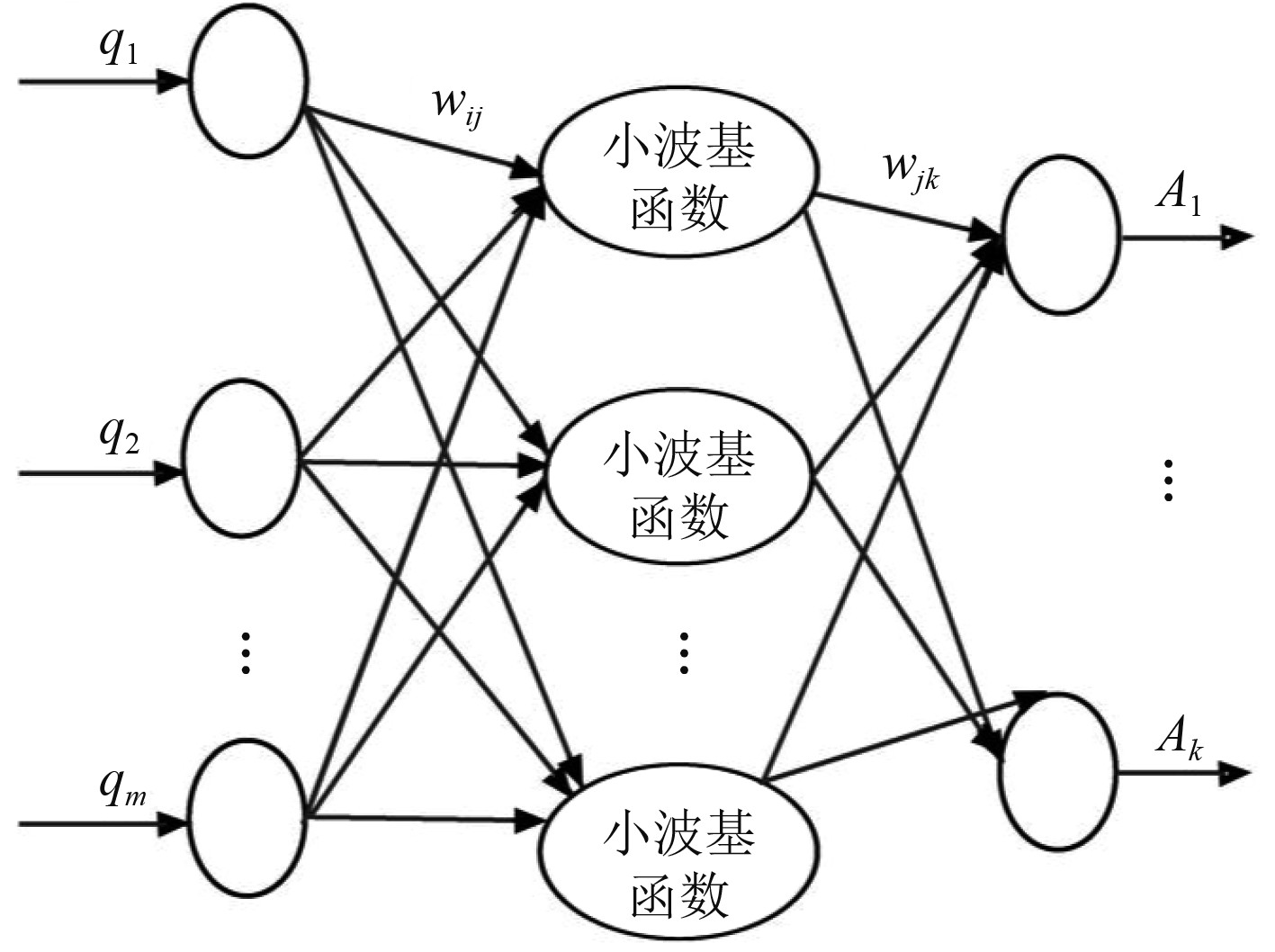
|
图 1 WNN模型结构 Fig. 1 WNN model structure |
WNN在设计结构上能够对目标函数进行快速的学习和功能进化,在整个交织网络的重要系数上进行由上至下的优化,展示出了一种分层的、多分辨率的小波神经网络模型,由此弥补了BP神经网络结构复杂的问题,可以很好地描述船用电控二冲程柴油机动力系统内部各部分间存在的联系。同时,该模型结构通过多层次的网络算法对信号进行小波变换处理,在功能上很好地替代了早期信号表达中的非线性sigmoid函数。
然而,目前关于动力系统可靠性预测模型的理论成果较少,未能成体系解决船用电控二冲程柴油机动力系统的排故问题。因此,适时对WNN在船用动力系统中的应用研究十分必要。WNN基于船用电控二冲程柴油机动力系统的相关参数进行自主学习,在船舶领域适应性强,在电力系统短期负荷预测方面也显示出了很大的优越性,具有较好的误差特性。本文以某远洋船舶为例,基于WNN对船用电控二冲程柴油机动力系统的可靠性进行模型构建,并验证其预测的可行性。
1 船用动力系统的辨识与测量 1.1 无功测量现代船用动力系统很多负载都具有非线性特征,会产生很大的谐波,影响电能质量。随着电力电子技术的发展,非线性负载不断增长,使电网产生了更多的不稳定因素。这些负载变化快,同时会给供电网络带来干扰,一般情况下也会引起电网电压波动,导致同一网络中的其他负载闪变[3]。同时,由于船用动力系统在不同时间内出现了新的负荷点或负荷值,使得系统中的功率因数发生改变,从而使整个供电系统产生不对称的畸变电流,引起电压升高,甚至导致变压器损坏。为应对这种瞬息万变的无功功率,一般都需安装无功补偿装置,以便对其动力系统输入信号进行捕捉。隐含层的输出信号hj公式如下:
| $ {h_j} = h\left( {\dfrac{{\displaystyle\sum\nolimits_{i = 1}^{i = m} {{w_{ij}}{x_i} - {b_j}} }}{{{a_j}}}} \right) \text{,} $ |
| $ j=1,2,\cdots m 。$ |
其中:bj为WNN的平移因子;h为WNN的无功测量函数;aj为WNN的伸缩因子。
然而在实际情况下,由于系统运行方式的改变或负载性质的不同而引起的无功功率波动是不可避免的,所以要想保证供电系统的安全经济运行就必须考虑无功功率的问题。
1.2 电压与电流波形实时识别无论是保护还是控制,都需要实时估算电流电压波形。为此,提出多种数值计算方法,如傅里叶级数、卡尔曼滤波技术等。其中,在船用动力系统暂态稳定分析方面使用较多的是时域分析法和频域分析法。但是这几种算法存在一定的局限性,在计算速度方面有较大限制,难以应用于船舶动力系统的保护和控制。
因此有学者开始对并行程序的设计进行研究,如用简单模拟处理器紧密地连接在一起,来求解优化问题与信号处理。在此基础上,WNN模型的出现,为信号恢复等许多信号处理问题开辟了新的前景。WNN一般采用连续时间优化算法,通过此算法可以大大提高系统的预测精度。
1.3 船用动力系统谐波源的监控与辨识谐波源实际上是一个非线性负载,这使得电压波形的畸变是不可接受的。就船用动力系统谐波分析而言,谐波源可通过状态估计方法识别。对于含有多个谐波源且不对称运行的系统,可以通过状态估计得到其各次谐波分量。但是这就要求船用动力系统必须安装大量的谐波测量装置,进而对船用动力系统谐波进行连续测量。本文研究的某远洋船舶的动力系统承受的谐波电压,就可以将其进行折算:
| $ {U_{ea}} = \sqrt {\sum\nolimits_{h = 1}^\infty {{{\left( {\frac{{{U_h}}}{{{h^m}}}} \right)}^2}} } 。$ |
其中:Uh为等价基波负序电压;Uea为第h次谐波电压;m为系数,且m≤1。
假设存在特征函数
| $ h(n) = {h_d}(n){w_R}(n) \text{,} $ |
| $ {w_R}(n) = \left\{ \begin{array}{ll} 1& 0 \leqslant n \leqslant N - 1,\\ 0& {\rm{others}}。\end{array} \right. $ |
为了获得足够的观测信息,必须对每个状态进行迭代求解。通常情况下,具有m个状态的网络需要至少m次复数测量才能计算出未知量,然后利用m+1次测量,对未知状态估计值进行改进。同时,为了提高系统的安全性和经济性,利用WNN对能源系统中非线性负荷的谐波源进行预估,在较少的点上连续测量谐波电流。
由于WNN具有学习能力和容错性能,因此其在运行中可以自动从大量输入数据中提取出有用信息,然后把这些估计值应用到状态估计器中,方便操作人员找到其他未知谐波源。
2 WNN在船用动力系统中的应用 2.1 应用思路采用WNN神经网络,将特高频传感器阵列得到的局部放电时延值用作输入矢量,其中时延误差修正的WNN模型如图2所示,采用有限标定点时延误差对WNN神经网络进行训练,以便模拟系统定位误差分布特征。
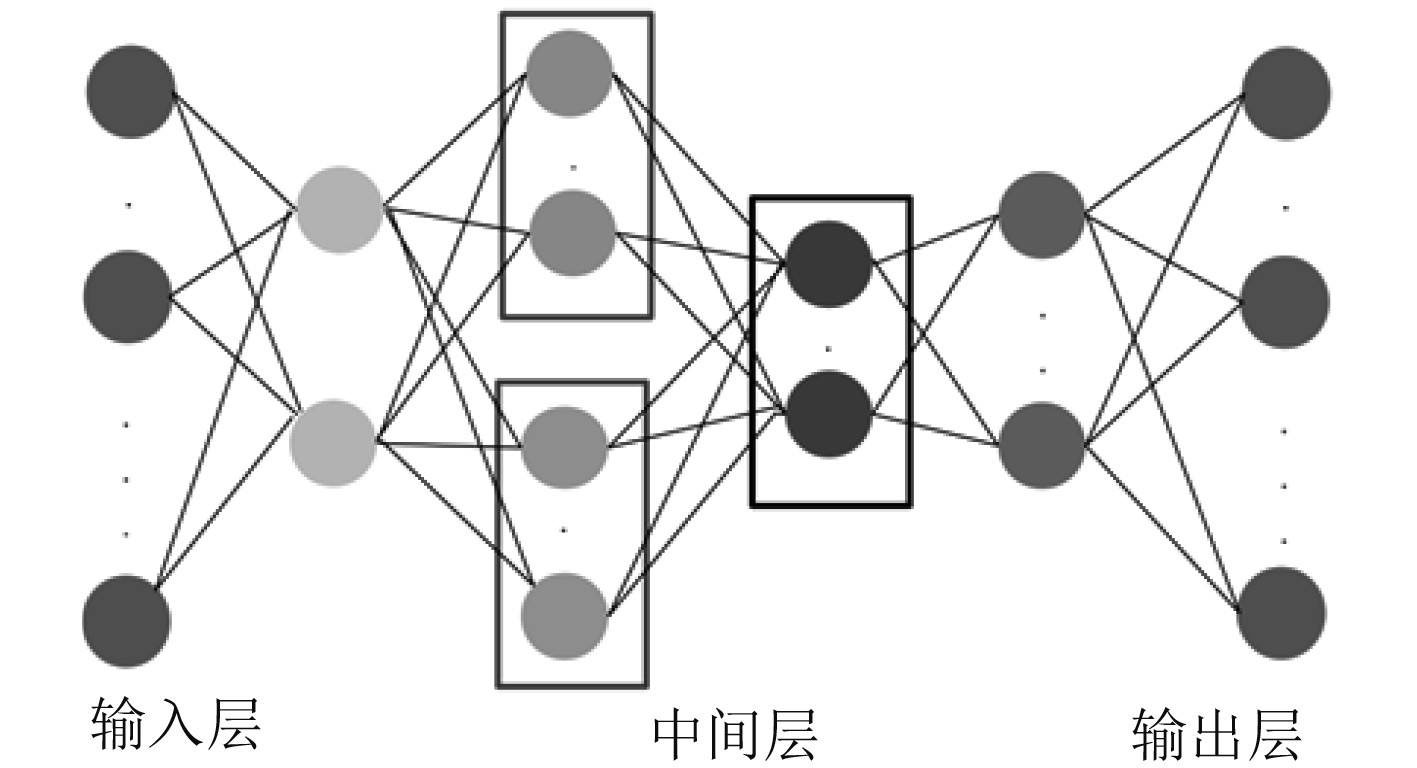
|
图 2 时延误差修正的WNN模型 Fig. 2 WNN neural network model for time delay error correction |
基于图2模型,在该远洋船舶动力系统的极径上设置如下3个区间:
| $ \begin{array}{l}{r}_{1}\in \left[2\;{\rm{m}}\text{,}6\;{\rm{m}}\right],\\ {r}_{2}\in \left[6\;{\rm{m}}\text{,}12\;{\rm{m}}\right],\\ {r}_{3}\in \left[12\;{\rm{m}}\text{,}18\;{\rm{m}}\right]。\end{array} $ |
在以上3个区间内分别建立WNN神经网络,校正实际定位结果,最终得出如图3所示修正模型。
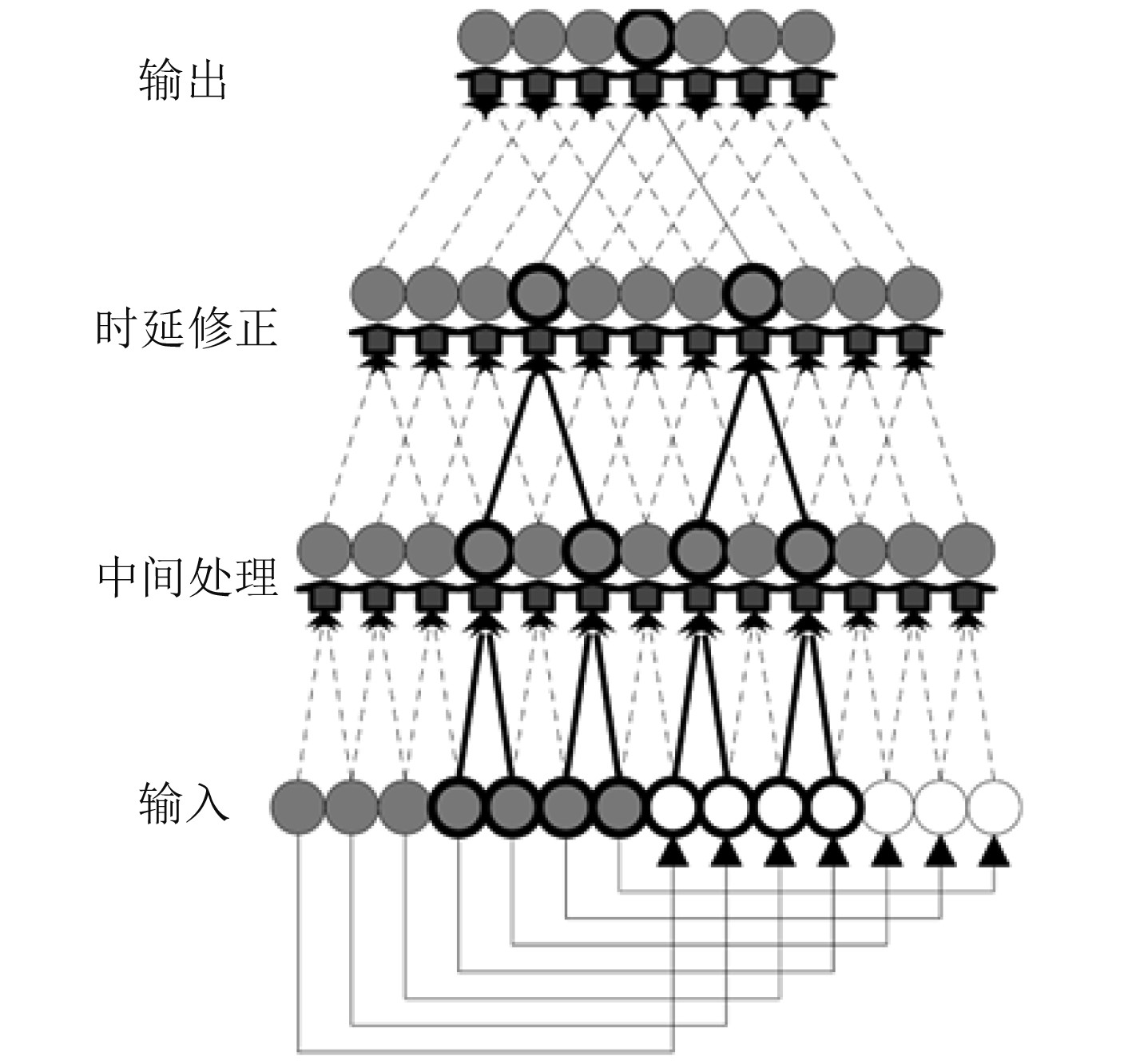
|
图 3 基于多WNN的局部放电时延误差修正模型 Fig. 3 Delay correction model for partial dischargebased on multiple WNNs |
未修正的局部放电定位试验结果见表1,利用WNN修正后的局部放电定位结果见表2。
|
|
表 1 未修正的局部放电定位结果 Tab.1 Uncorrected partial discharge location results |
|
|
表 2 利用WNN修正后的局部放电定位结果 Tab.2 Partial discharge localization results after WNN correction |
对比表1与表2的修正结果可知,利用WNN修正后的局部放电定位结果其距离误差和角度误差都明显更小。基于距离误差、角度误差以及修正前后的参数可知,采用多WNN校正时延误差,其定位精度有所提高,距离误差可控制在−1.05 m以内,角度测量误差可控制在0.58°以内,从而在一定程度上提升了船用动力系统装置电力稳定性,进而降低了该电控柴油机的误差范围。
3 WNN在船用动力系统中的应用测试对该远洋船舶的动力系统可靠性构建训练模型,通过搭建测试集来验证其预测的可行性。
模型整体预测图如图4所示,基于WNN的船用动力系统可靠性测试的上半部分,展示了该预测模型对全体数据集的总体预测效果以及预测具体数值。其中,部分是数据集上观测的原始数据,最后线条是该模型所预测的数据。在最终的结果呈现上依旧是原来一个完整的数据集。
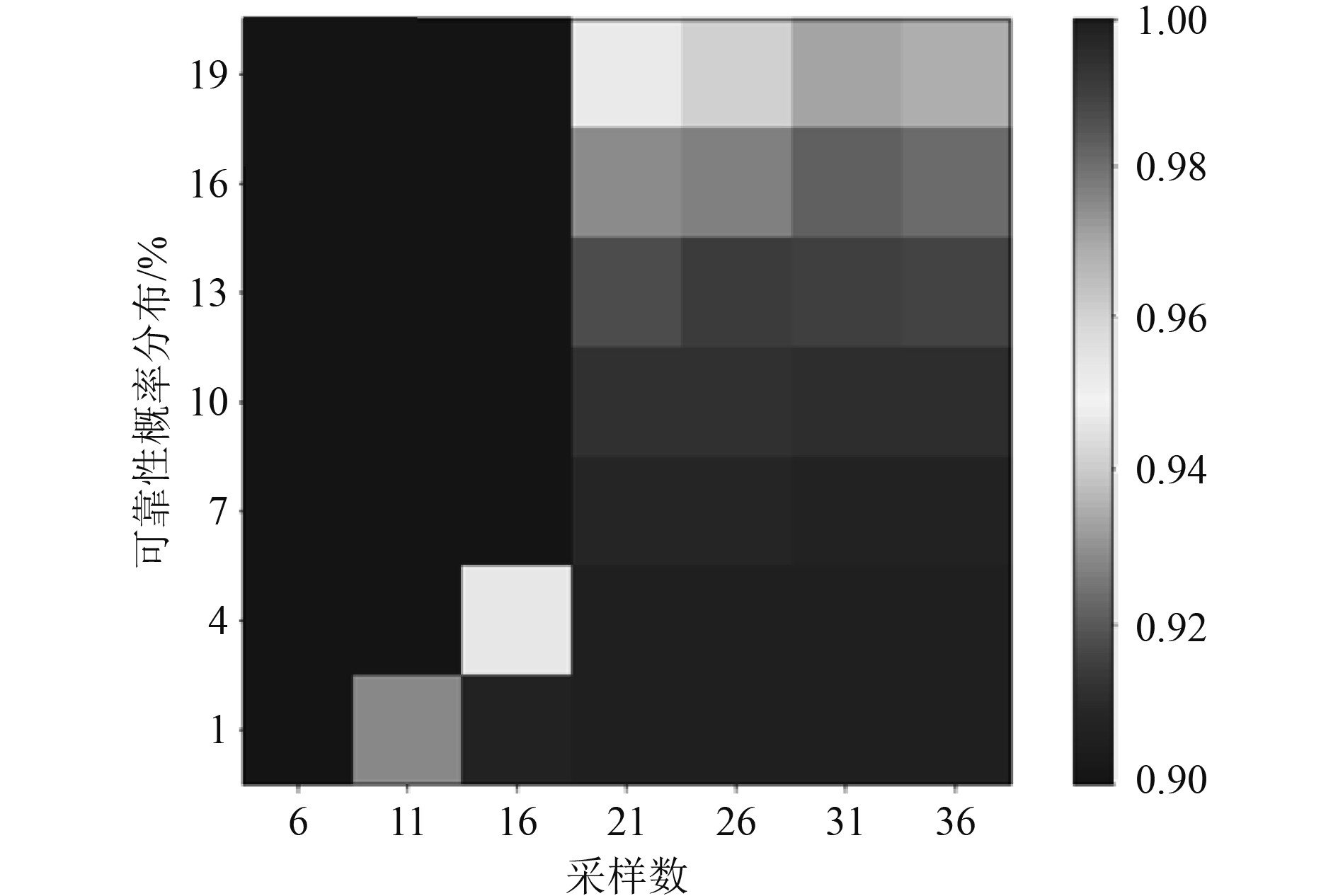
|
图 4 模型整体预测图 Fig. 4 Overall prediction diagram of the model |
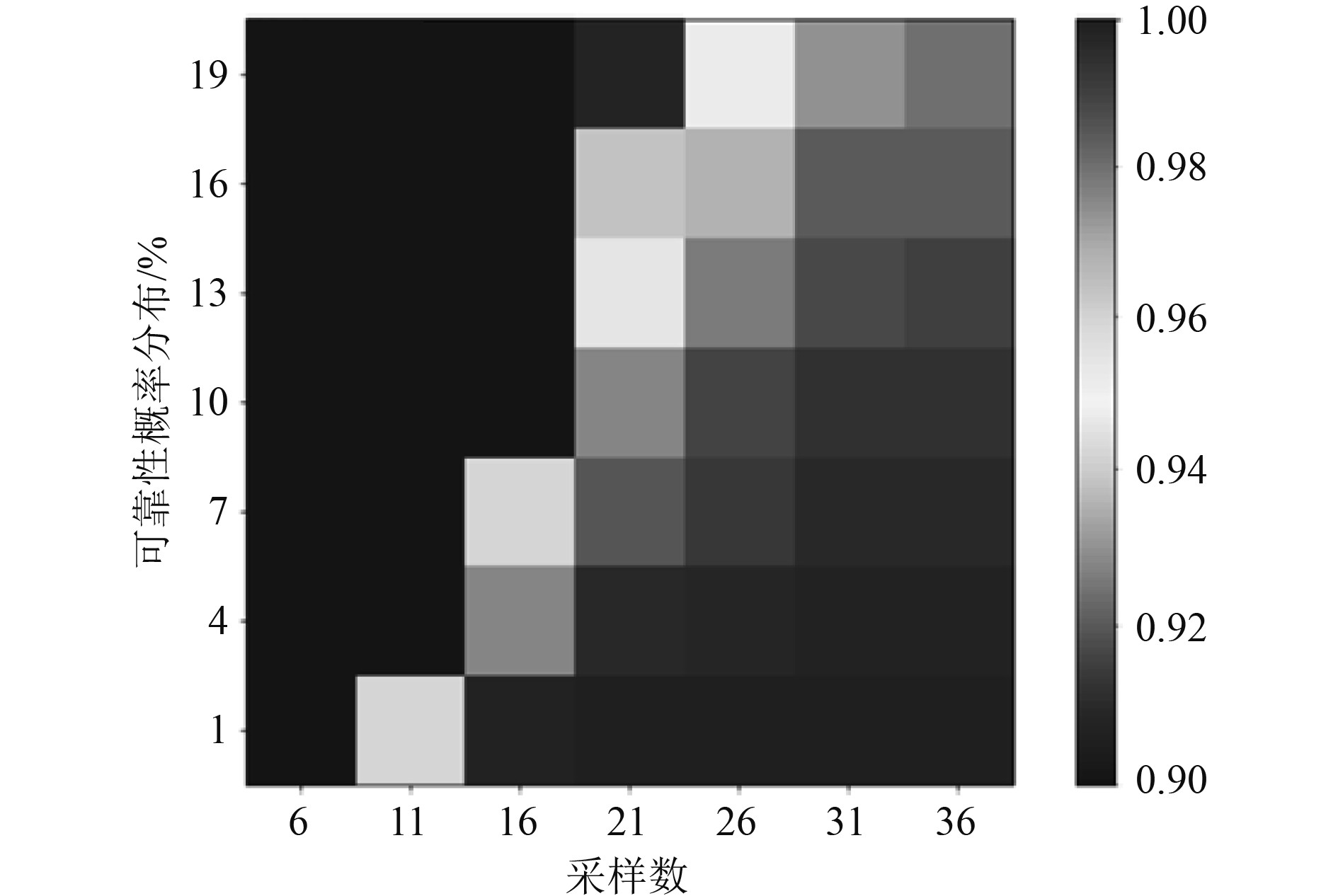
此外,图4中白色区域为模糊区域,该区域的状态受到采样数量的影响。左右两部分的观察结果为预测总体结果,通过分析预测数据和原始数据,其总体变化表现为趋近于一个较为规律的变化波形,随着采样数量的增多,可靠性结果的概率分布也逐渐趋近于1。并且该成果符合基于WNN预测船舶动力系统故障的预测特征,说明本研究在最终的结果呈现上具有一定的科学性。
图5为该模型所预测数据和原始数据的差异。可以看出,该模型不管是从预测趋势,还是最终的仿真数据值看几乎是一致的。
|
图 5 模型局部预测图 Fig. 5 Local prediction diagram of the model |
通过归纳和总结,尽管预测数据和原始数据间存在着误差,但是依然可以利用小波算法对原始数据进行有效的处理,从而进一步提高预测的精度。
由此得出,采取WNN进行船用动力系统的可靠性预测,其误差能控制在预估范围内,且该结果可接受。
综上所述,基于WNN的船舶动力控制系统能够很好地对船舶的可靠性进行预测和诊断,并且这种智能控制可以对电控柴油机动力系统在运行过程中起到继电保护的作用,不仅相比传统的计算方式更加便捷,而且还具备负荷预测等功能。
4 结 语本文以某远洋船舶为例,基于小波变换理论,将其与WNN模型相结合,用于船舶动力系统的电控柴油机观察及预测。该方法可以自动适应时频信号分析要求,专注于信号的每一个细节,解决复杂的傅里叶变换问题。
| [1] |
杨超, 张霖, 申峻. 基于小波神经网络的变压器油温预测[J]. 电气开关, 2022, 60(6): 58-62. YANG Chao, ZHANG Lin, SHEN Jun. Transformer oil temperature prediction based on wavelet neural network[J]. Electrical Switch, 2022, 60(6): 58-62. DOI:10.3969/j.issn.1004-289X.2022.06.014 |
| [2] |
彭峰, 王林. 耦合自相关理论与小波神经网络的地下水模拟预测模型[J]. 红水河, 2021, 40(2): 96-100. PENG Feng, WANG Lin. Groundwater simulation and prediction model coupled with autocorrelation theory and wavelet neural network[J]. Hongshui River, 2021, 40(2): 96-100. |
| [3] |
黄欢, 李文雄, 李俞谕, 等. 非平稳随机激励下线性结构动力响应的小波多尺度分析[J]. 地震工程与工程振动, 2023, 43(1): 177-188. HUANG Huan, LI Wen-xiong, LI Yu-yu, et al. Wavelet multiscale analysis of dynamic response of linear structures under non-stationary random excitation[J]. Earthquake Engineering and Engineering Vibration, 2023, 43(1): 177-188. |
| [4] |
林华钊, 王迪, 鲁国阳. 基于改进Laplace小波和改进卷积神经网络的压裂车动力端轴承故障识别[J]. 机电工程, 2023, 40(5): 691-698. LIN Hua-zhao, WANG Di, LU Guo-yang. Fault identification of power end bearing of fracturing vehicle based on improved Laplace wavelet and improved convolutional neural network[J]. Electromechanical Engineering, 2023, 40(5): 691-698. DOI:10.3969/j.issn.1001-4551.2023.05.007 |
| [5] |
孙文, 梁庆国, 乔向进, 等. 不同失稳形态黄土边坡的动力响应研究[J]. 铁道学报, 2022, 44(6): 123-130. SUN Wen, LIANG Qing-guo, QIAO Xiang-jin, et al. Research on Dynamic Response of Loess Slopes with Different Instability Forms[J]. Journal of Railway Science, 2022, 44(6): 123-130. DOI:10.3969/j.issn.1001-8360.2022.06.015 |
| [6] |
王延仓, 李笑芳, 李莉婕, 等. 基于离散小波-微分变换算法定量反演火龙果茎枝叶绿素含量的研究[J]. 光谱学与光谱分析, 2023, 43(2): 549-556. WANG Yan-cang, LI Xiao-fang, LI Li-jie, et al. Quantitative inversion of chlorophyll content in pitaya stems and branches based on discrete wavelet-differential transform algorithm[J]. Spectroscopy and Spectral Analysis, 2023, 43(2): 549-556. |
 2023, Vol. 45
2023, Vol. 45
