2. 中国人民解放军91550部队,辽宁 大连 116021
2. No. 91550 Unit of PLA, Dalian 116021, China
近年来,世界各主要军事强国高度重视水下无人装备的发展,无人潜航器在水文探测、监视与侦察、反水雷、反潜等任务方面发挥着重要作用,是未来水下作战体系中不可或缺的无人作战力量[1]。为有效提升无人潜航器在执行任务中的作战效能,有必要对其规划航迹进行评价。
航迹评价是指在航迹规划完成后,根据具体的任务要求,利用评价算法对一组航迹或几组航迹进行评价,从中选择出一条或者一组最优航迹。航迹规划中自身性能、战略和战术等约束条件的存在,使得潜航器航路评价也将是一个复杂的多属性决策问题[2-3]。当前的航迹评价领域中,常用的多属性评价方法有简单加权法(SAW)[4]、层次分析法(AHP)[5-6]、逼近理想排序方法(TOPSIS)[7-8]和ELECTRE方法[9-10]等。上述方法都将判断矩阵的构建作为核心,决策者对于最终的评价结果影响非常大,缺点明显。如何减少主观因素对无人潜航器航迹评价的影响,并开展科学准确的航迹评价方法研究十分必要。
本文首先对基于TOPSIS的评价体系方法及流程进行分析,构建了航迹评价指标模型;其次结合主观赋权法和客观赋权法特点[11-13],提出主客观均衡赋权的航迹评价方法。最后,给出了航迹综合评价仿真验证结果。结果表明,所提方法可提高无人潜航器航迹评价结果的准确性及合理性。
1 基于TOPSIS的评价体系 1.1 评价体系构建本文将众多约束条件进行综合,概括为无人潜航器的性能约束、环境威胁约束、敌方威胁区约束,根据上述约束条件构建航迹评价指标体系。
建立的航迹评价指标体系,充分考虑了影响航迹优劣的各种约束条件,为后续各项指标的约束建模奠定基础。
1.2 航迹评价流程1)构建标准化决策矩阵
设有
| $ {a_{ij}} = \frac{{{x_{ij}}}}{{\sqrt {\displaystyle\sum\nolimits_{i = 1}^n {x_{ij}^2} } }}。$ | (1) |
得到归一化处理后的决策矩阵为:
| ${\boldsymbol{ A }}= \left[ \begin{gathered} {a_{11}}{\text{ }}{a_{12}}{\text{ }} \cdots {\text{ }}{a_{1m}} \\ {a_{21}}{\text{ }}{a_{22}}{\text{ }} \cdots {\text{ }}{a_{2m}} \\ \ldots {\text{ }} \ldots {\text{ }} \ldots {\text{ }} \ldots {\text{ }} \\ {a_{n1}}{\text{ }}{a_{n2}}{\text{ }} \cdots {\text{ }}{a_{nm}} \\ \end{gathered} \right] 。$ | (2) |
2)确定正负理想解
正理想解是指最优方案的各个属性值都达到最好的值,而负理想解是指设想的最劣解,即各个属性值都为最劣值,具体如下:
正理想解:
负理想解:
3)计算各方案到正负理想解的距离
设
| $ D_i^ + = \sqrt {\sum\nolimits_{j = 1}^m {{\omega _j}{{\left( {a_i^ + - {a_{ij}}} \right)}^2}} },$ | (3) |
| $ D_i^ - = \sqrt {\sum\nolimits_{j = 1}^m {{\omega _j}{{\left( {a_i^ - - {a_{ij}}} \right)}^2}} } 。$ | (4) |
式中,
4)计算各待评价方案与最优方案的接近程度
设
| $ {C_i} = \frac{{D_i^ - }}{{D_i^ + + D_i^ - }}。$ | (5) |
其中:
根据图1所示的综合指标体系进行约束建模。
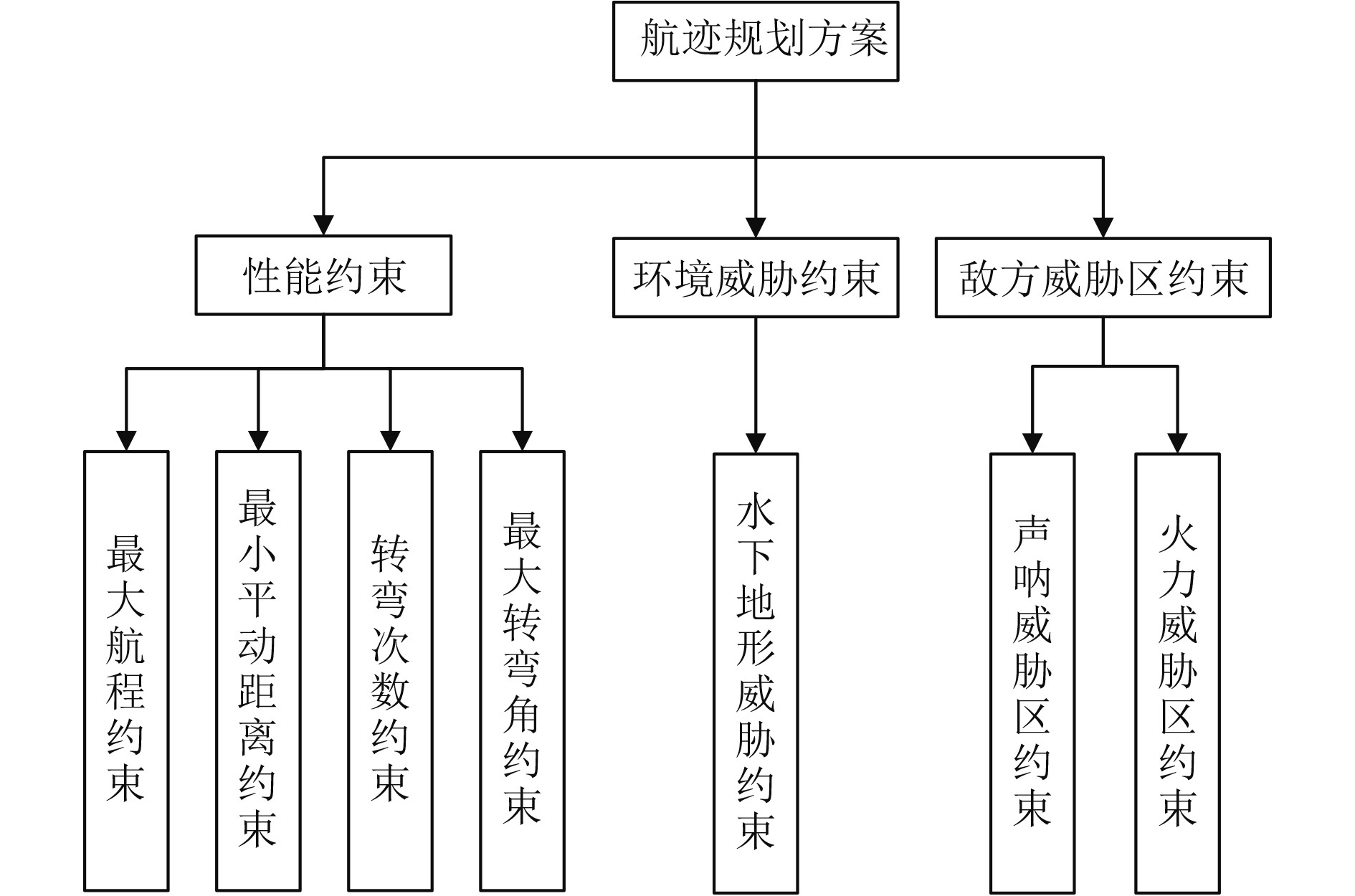
|
图 1 潜航器航迹综合评价指标体系 Fig. 1 Comprehensive evaluation index system for submarine trajectory |
1)最大航程约束指标
由于潜航器自身燃料及任务时长的限制,规划航迹总长超出最大航程范围将会导致任务失败,因此将最大航程约束作为评价的指标之一。如图2所示,A、B点为起始和目标点,某子航段

|
图 2 潜航器航迹规划示意图 Fig. 2 Schematic diagram of submarine trajectory planning |
| $ \left\{ \begin{gathered} {l_i} = \bar v \cdot {t_i}{\text{ }}(0 < {t_i} \leqslant T) ,\\ \mathop \sum \nolimits_{i = 1}^n {l_i} \leqslant {l_{max}}{\text{ }}(0 < i \leqslant {\text{n}}) 。\\ \end{gathered} \right. $ | (6) |
2)最短平动距离约束指标
潜航器执行任务的过程中,需做一些机动动作来避开威胁区域,在完成上一次机动后,必须直行一段距离进行姿态调整。设2次机动间的最短距离为
| $ {l_i} \geqslant {l_{\min }}{\text{,}}{i = 1,2, \ldots ,n} 。$ | (7) |

|
图 3 两机动位置间最短平动距离示意图 Fig. 3 Schematic diagram of the shortest translational distance between two maneuvering positions |
3)转弯次数约束指标
潜航器进行机动转弯时,自身状态会随姿态发生变化,如果转弯次数过多,其稳定性将会降低,因此转弯次数有上限值。设无人潜航器沿预规划航迹运动时转弯次数为
| $ N \leqslant {N_{\max }} 。$ | (8) |
4)最大转弯角约束指标
最大转弯角示意图如图4所示。

|
图 4 最大转弯角示意图 Fig. 4 Schematic diagram of maximum turning angle |
潜航器进行机动转弯时的转弯角如果超过最大转弯角,则会使其脱离预规划航迹,那么在航点处的转弯角
| $ \Delta \theta = \left| {{\theta _i} - {\theta _{\max }}} \right|,{i = 1,2, \ldots ,n} 。$ | (9) |
式中,
5)水下地形威胁约束指标
潜航器在水下工作时需要与水下山体等威胁保持安全距离。以山体为例建模,设单个山峰的高度为Z,则
| $ Z = z \cdot \exp \left[ { - {{\left( {\frac{{x - {x_1}}}{a}} \right)}^2} - {{\left( {\frac{{y - {y_1}}}{a}} \right)}^2}} \right] + {z_0} 。$ | (10) |
式中:
当潜航器在某一高度

|
图 5 水下地形威胁区示意图 Fig. 5 Schematic diagram of underwater terrain threat zone |
设某点处潜航器的位置坐标为
| $ \sqrt {{{\left( {{x_i} - {x_1}} \right)}^2} - {{\left( {{y_i} - {y_1}} \right)}^2}} - \alpha \geqslant {d_1}。$ | (11) |
6)声呐探测威胁区约束指标
潜航器在执行任务过程中,需避开敌方水下探测区域并保持一定距离,以降低我方被敌方目标发现的几率。水下常用声呐装置进行目标探测,声呐可发射超声声波脉冲,超声波在水中能量衰减小,传播速度快,当遇到有密度变化的物体会发生反射作用。根据声呐探测目标的基本原理,可得距离为:
| $ {d_2} = \frac{1}{2}\left( {\Delta t \times c} \right) 。$ | (12) |
式中:
设我方潜航器被声呐发现的概率为
| $ P \propto \frac{1}{{{d_2}}}。$ | (13) |
7)火力威胁约束指标
为保证潜航器能够安全到达目标区域,不仅要避开敌方探测区域,还应尽量避免穿越敌方火力打击区域。敌方的水下武器一般包括鱼雷、水雷和深水炸弹,此类武器在水下爆炸时,会产生高压球形气团的脉动循环破坏作用,对所打击目标造成严重毁伤,使潜航器失去执行任务的能力。设最大毁伤半径为
| $ \sqrt {{{\left( {{x_i} - {x_2}} \right)}^2} - {{\left( {{y_i} - {y_2}} \right)}^2}} - {R'_{\max }} \geqslant {d_3} 。$ | (14) |
根据航迹指标约束建模,在TOPSIS算法流程的基础上,采用混合主观和客观的评价方法,对综合权重进行优化,得到最终的权重值。

|
图 6 AHP-EWM的权重确定 Fig. 6 Weight determination of AHP-EWM |
利用层次分析法计算得到的各指标主观权重值和熵权法计算得出的客观熵权值,通过均衡策略赋予两者的影响因子都为0.5,得到各评价指标的综合权重值为:
| $ {\omega _i} = \frac{1}{2}{\omega '_i} + \frac{1}{2}{\omega ''_i} 。$ | (15) |
最终,评价指标的综合权重集为:
利用层次分析法(Analytic Hierarchy Process,AHP)法求取各评价指标主观权重的计算过程如下:
1) 构造判断矩阵
根据建立的静态航迹评价指标体系,确定上层指标所属下层指标对其影响所占比重,构建的判断矩阵为:
| $ {\boldsymbol{A }}= \left[ \begin{gathered} {a_{11}}{\text{ }} \cdots {\text{ }}{a_{1n}} \\ {\text{ }} \vdots {\text{ }} \vdots \\ {a_{n1}}{\text{ }} \cdots {\text{ }}{a_{nn}} \\ \end{gathered} \right]。$ | (16) |
其中,
|
|
表 1 评价指标相对重要程度标度表 Tab.1 Scale of relative importance of evaluation indicators |
因此,将自身性能约束
2) 层次单排序
计算各指标权重,进行层次单排序,包括:对判断矩阵的每一列进行归一化处理;将归一化后的判断矩阵按列求和,并归一化处理;计算判断矩阵的最大特征根。
| $ \lambda = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{{{\left( {Aw} \right)}_i}}}{{{w_i}}}} 。$ | (17) |
3) 判断矩阵的一致性检验
对一级指标和二级指标中所求权重进行一致性检验。
| $ CR = \frac{{{\lambda _{\max }} - n}}{{RI\left( {n - 1} \right)}} 。$ | (18) |
式中:
求得各级指标单层权重后,将二级指标的权重向量乘以相应的一级指标的权重,求得指标层各指标在整个评价体系中的总权重,则航迹评价指标的总主观权重集为:
| $ \omega ' = \left\{ {{{\omega '}_1},{{\omega '}_2}, \ldots ,{{\omega '}_7}} \right\} 。$ | (19) |
利用熵权法(Entropy Weight Method,EWM)求取各评价指标客观权重的计算过程如下:
1) 指标层数据标准化
设待评价航迹有
| $ {\boldsymbol{X}} = \left[\begin{array}{ccccccccc} {X_{11}}&{X_{12}}& \cdots &{X_{17}} \\ {X_{21}}&{X_{22}}& \cdots &{X_{27}} \\ \vdots & \vdots & {\boldsymbol{}}&\vdots \\ {X_{m1}}&{X_{m2}}& \cdots&{X_{m7}} \\ \end{array} \right] 。$ | (20) |
2) 原始数据矩阵归一化处理
由于航迹规划方案所涉及的7个指标的量纲各不相同,而且数值差异也较大。为使各指标具备可比性,必须对各指标的数据进行归一化处理。
对于越大越优型指标,如声呐威胁区约束指标等评价指标,进行归一化处理:
| $ {V_{ij}} = \frac{{{x_{ij}} - \min ({x_j})}}{{\max ({x_j}) - \min ({x_j})}} 。$ | (21) |
其中,
而对于越小越优型指标,如最大航程约束指标、转弯次数约束指标等评价指标,利用式(22)进行归一化处理:
| $ {V_{ij}} = \frac{{\max ({x_j}) - {x_{ij}}}}{{\max ({x_j}) - \min ({x_j})}} 。$ | (22) |
其中,
3) 各评价对象的特征比重计算
设第
| $ {P_{ij}} = \frac{{{V_{ij}}}}{{\sum\nolimits_{i = 1}^m {{V_{ij}}} }}。$ | (23) |
式中,
4) 第
设第
| $ {e_j} = - \frac{1}{{\ln m}}\sum\limits_{i = 1}^m {{P_{ij}} \cdot \ln {P_{ij}}} ,$ | (24) |
| $ {D_j} = 1 - {e_j} 。$ | (25) |
5) 计算各评价指标的权重
设第
| $ {{{\boldsymbol{\omega}} }^{″}}_{j}=\frac{{D}_{j}}{{\displaystyle {\sum }_{j=1}^{7}{D}_{j}}} 。$ | (26) |
因此,可得航迹评价指标的客观权重集为:
设定评价指标的初始数据,如表2所示。
|
|
表 2 航迹初始化参数设置表 Tab.2 Track initialization parameter setting table |
设定潜航器的规划航迹有5条,各航迹的具体指标数据如表3所示。其中,水下地形威胁区、声呐探测区和敌方火力威胁区均被视作不可穿越区,此可将无人潜航器与各类威胁区的距离简化为至威胁区的最短距离。
|
|
表 3 规划航迹评价指标值 Tab.3 Evaluation index value of planned flight path |
解算得指标综合权重集为:
| $ \begin{split} {\boldsymbol{\omega}} & =\left\{{\omega }_{1},{\omega }_{2},\dots ,{\omega }_{5}\right\}=\\ & \left\{0.1301,0.1311,0.1576,0.1227,0.1625\right\}。\end{split} $ |
由图7可知,各航迹规划方案的评分为:79、82、93、85、87。对上述航迹进行优劣排序为:航迹3、航迹5、航迹4、航迹2、航迹1。因此,上述航迹规划方案中标号为3的航迹为潜航器的最优航迹。
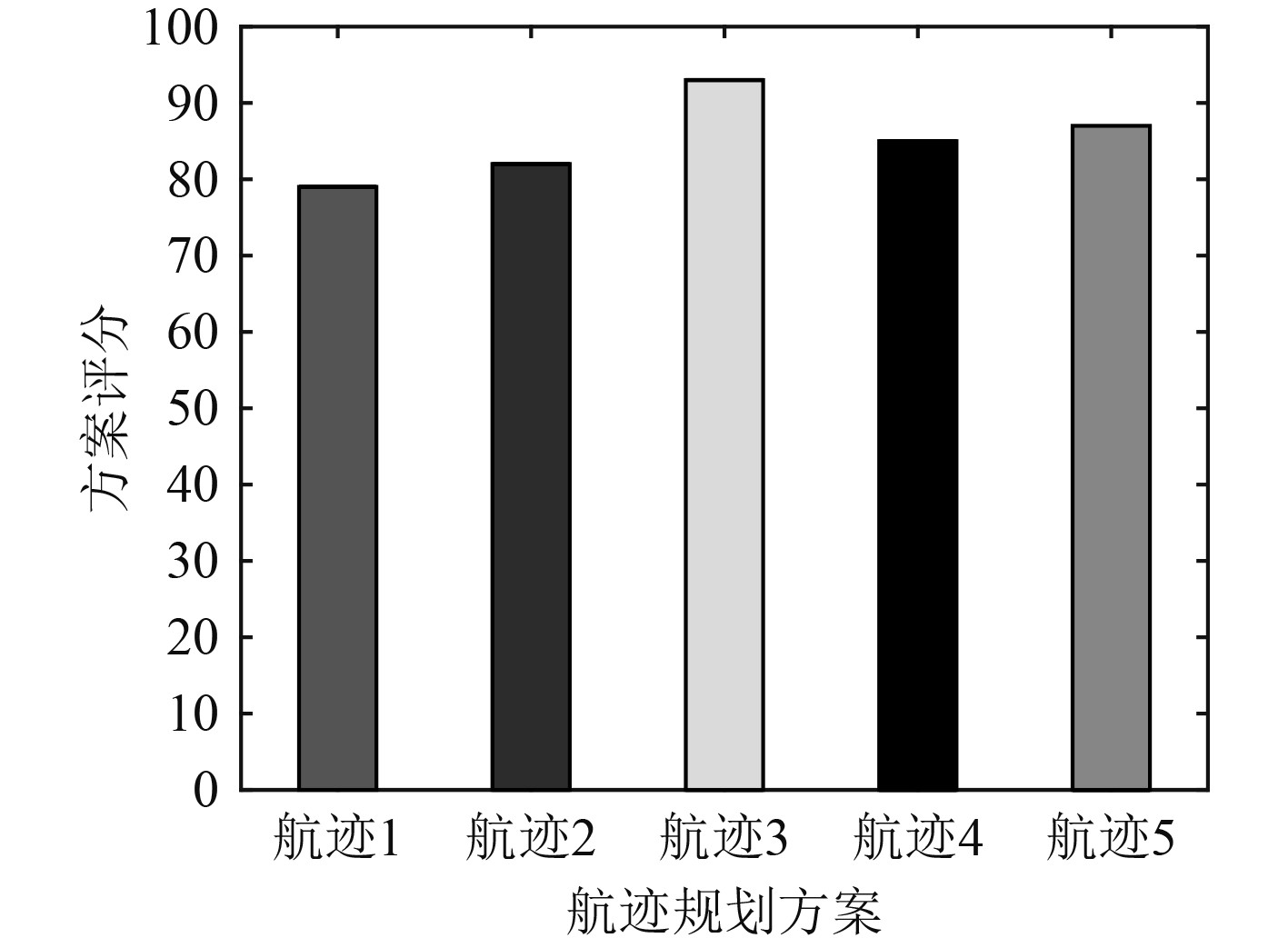
|
图 7 航迹方案评价结果示意图 Fig. 7 Schematic diagram of the evaluation results of the trajectory plan |
通过仿真分析,将综合权重与主观权结果、客观权重结果对比可知,本文的综合权重计算方法整体考虑了各指标的主观权重与客观权重,最大程度上削减主观权重与客观权重在某些指标权重分配差异过大对最终评估结果的影响,提高评价结果的科学性及合理性。
5 结 语本文面向无人潜航器最优航迹评价中权重的合理分配问题,基于TOPSIS算法,构建了规划航迹的多层级评价指标模型,采用主观和客观结合的均衡策略,提出了AHP-EWM均衡赋权法。针对随机5条规划航迹进行了评价方法的试验验证,得到了该潜航器的最优航迹。该方法避免了决策者对评价过程的过度干预,综合衡量主观权重与客观权重的比重,从而使最终的航迹评价结果更加准确、可信。未来研究中可建立不同潜航器的仿真模型,通过大量的原始数据仿真,建立起各类型潜航器的拟合关系库,扩大该航迹评价方法的适用范围。
| [1] |
冯景祥, 姚尧, 潘峰, 等. 国外水下无人装备研究现状及发展趋势[J]. 舰船科学技术, 2021, 43(12): 1-8. |
| [2] |
ZHANG D Q, ZHAO J F, WANG M H, et al. Grey evaluation and optimization of UAV’s path planning method [C]//A//2010 2nd International Conference on Electronic Computer Technology(ICECT 2010): 85–88.
|
| [3] |
SWARTZENTRUBER L, JUNG LENG, ELIOT H Winer. Multi-Objective UAV path planning with refind reconnaissance and threat formulations [C]// AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference<BR>18th12-15 April 2010, AIAA 2010–2758.
|
| [4] |
李维. 基于多属性决策方法的评价及灵敏度分析 [D]. 上海: 东华大学, 2007.
|
| [5] |
朴春华. 层次分析的研究与应用 [D]. 北京: 华北电力大学, 2008.
|
| [6] |
李枭扬, 周德云, 邹奥. 基于AHP-TOPSIS算法的多航迹评价 [J]. 第四届中国航空兵器大会论文集, 2015: 1–4.
|
| [7] |
龚剑, 胡乃联, 崔翔, 等. 基于AHP-TOPSIS评判模型的岩爆倾向型预测[J]. 岩石力学与工程学报, 2014, 33(7): 1442-1448. |
| [8] |
YU Y, LIANG L, JIANG Y J, et al. A new modified approach of TOPSIS based on fuzzy preference[J]. Systems Engineering, 2004, 8(22): 87-90. |
| [9] |
左军. 多目标决策分析 [M]. 浙江: 浙江大学出版社, 1991.
|
| [10] |
HWANG C L, MASUD A. Multiple objective decision making methods and applications [M]. Springer Verlag, N. Y. , 1979.
|
| [11] |
朱振强. 飞行器航路规划与评价研究 [D]. 西安: 西安电子科技大学, 2014.
|
| [12] |
张淘沙, 鲁艺. 基于BP神经网络的UCAV航迹综合评价[J]. 火力与指挥控制, 2017, 42(7): 153-160. |
| [13] |
张瑞玲. 基于多目标的航迹评价方法[J]. 黑龙江科技信息, 2013, 27: 51-52. |
 2023, Vol. 45
2023, Vol. 45
