2. 驻马店职业技术学院,河南 驻马店 463000
2. Zhumadian Vocational and Technical College, Zhumadian 463000, China
破冰船作为一种在冰冻水域开辟航道的特殊用船,最早源于16世纪的俄国,并以简易的雪橇形状出现。一开始该船型仅适用于薄冰区,到了19世纪末,德国造船工程师参照布利聂夫的图纸设计出了可用于港口附近和近海领域的破冰船,成为了当代破冰船的雏形[1-3]。目前较为常见的破冰船,具有以下几个典型特征:1)破冰船的长宽比与一般海船相比差别较大,比如我国用E级钢板制作的“雪龙”号,其船首外壳处至少要用5 cm厚的钢板制成,而瑞典破冰船ODEN号,其钢材最厚处更是达到了6 cm;2)破冰船的内部结构,与其他船舶相比其抗冰性能需要更强,并需预留较大的空间,方便破冰船配备直升机用于冰区勘测和导航;3)破冰船在操纵性方面,为更好地适应极地区域行驶,破冰船在外部结构上需要采用大功率旋转推进器,由此提升破冰船在开阔水域的机动性。
有限元分析软件是在建立的3D模型基础上对其建立数学模型,然后再对其进行分析模拟评估,一般的有限元分析都可以分析各式各样的工程、零件强度检验等问题,且有限元分析大概可包括静力学分析、流体力学分析、热力传输分析和抗疲劳分析检验等[4--6]。
1 破冰船模型构建 1.1 破冰船三维模型本文以某破冰船为研究对象,经实际测量后得到破冰船具体参数如表1所示。
|
|
表 1 某破冰船基本参数 Tab.1 Basic parameters of a Icebreaker |
基于以上参数,利用Solid Works2018软件对破冰船的船体结构进行建模,通过建立各部分零件图,再将其进行装配。构建三维模型过程如下:
1)首先测量破冰船船体的结构参数,再对三维实体进行圆角、抽壳和镜像,获得整个破冰船船体结构。
2)通过对破冰船圆孔进行二维处理,绘制相应的圆弧,拉伸得到加强圈,然后在后盖面绘制圆孔并切除。
3)半轴套管为上下对称结构,建立其对应的立体模型,然后再旋转得到虚拟模型。
4)侧边轮廓为左右对称结构,旋转拉伸得到三维立体模型。
5)最后打开Solid Works新建装配图,导入上述步骤获得的各零件参数,设置相应的环境界面后就完成所有的几何建模工作。
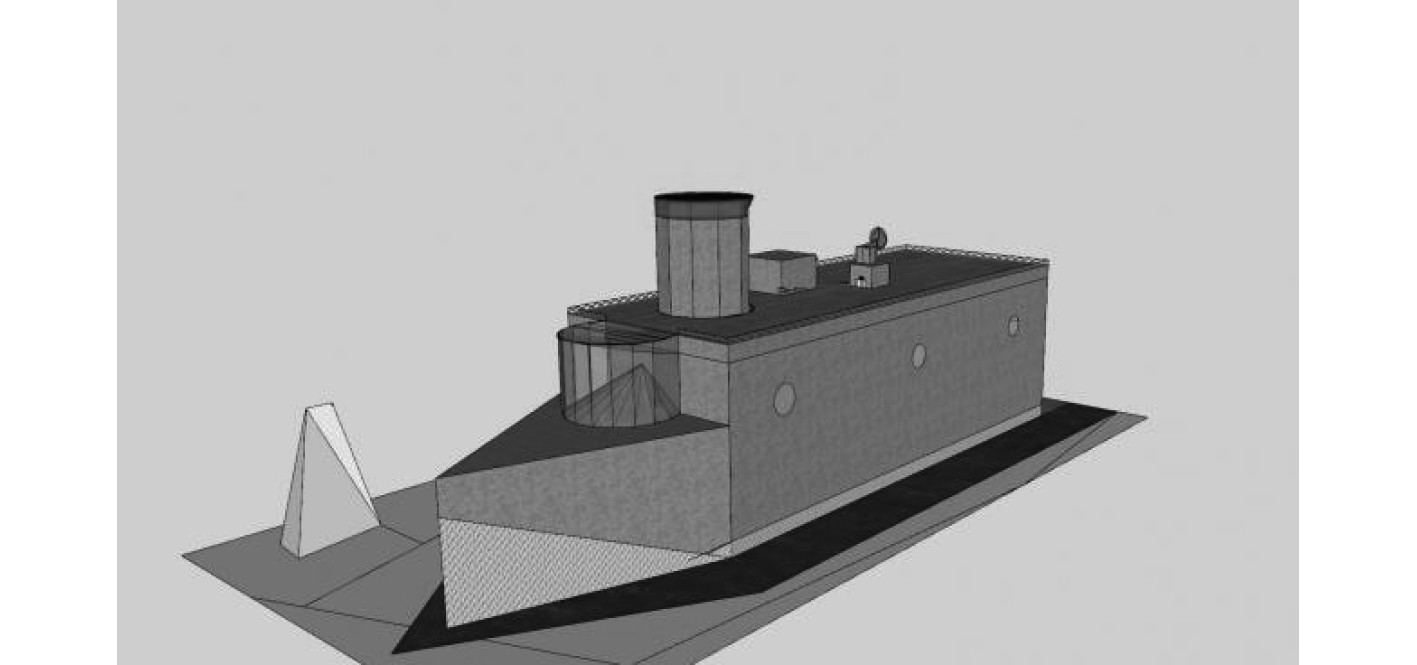
破冰船三维建模及结构装配体完成后,得出破冰船三维模型构建如图1所示。
|
图 1 破冰船三维模型构建 Fig. 1 3D model construction of Icebreaker |
本次物理建模使用的3D绘图软件是Solid Works,在选择有限元软件时,直接选择Solid Works中自带的有限元分析插件,一方面有效解决了建模软件与分析插件的适配问题,提高了设计的效率和准确性;另一方面,在使用配套插件Simulation时,也可以对破冰船在不同工况条件下的功能进行分析,且操作较为简单。步骤如下:
步骤1 找到simulation插件并打开;
步骤2 点击新算例,新建有限元分析算例,在此使用的是静应力分析;
步骤3 点击网格,对物理模型生成网格;
步骤4 点击夹具顾问,选择固定方式;
步骤5 打开应用材料,选择设计物体所需要的材料,本设计选择铸造钢;
步骤6 添加外部载荷,选择物体所要承受的外部载荷受力;
步骤7 运行算例,生成结果,分析模型是否达到要求。
2 基于有限元的破冰船静力学计算力学强度的理论计算,较为常用的有以下几种:1)拉断力计算时可以采用强度理论进行分析,从而判断破冰船在材料属性的脆性程度;2)屈服强度可采用屈服强度理论进行分析,从而判断破冰船在材料属性的塑性程度。本文根据破冰船的双重材料属性再结合破冰船工作状况,对选取的材料和结构进行强度分析。
屈服强度理论函数如下:
| $ \sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _1} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2}} \right]} \leqslant \left[ \sigma \right] 。$ |
式中,σ1为x方向的主应力,σ2为y方向的主应力,σ3为z方向的主应力。通过有限元法分析结构所受到的最大应力,并与材料的强度进行对比,从而进行结构的优化。
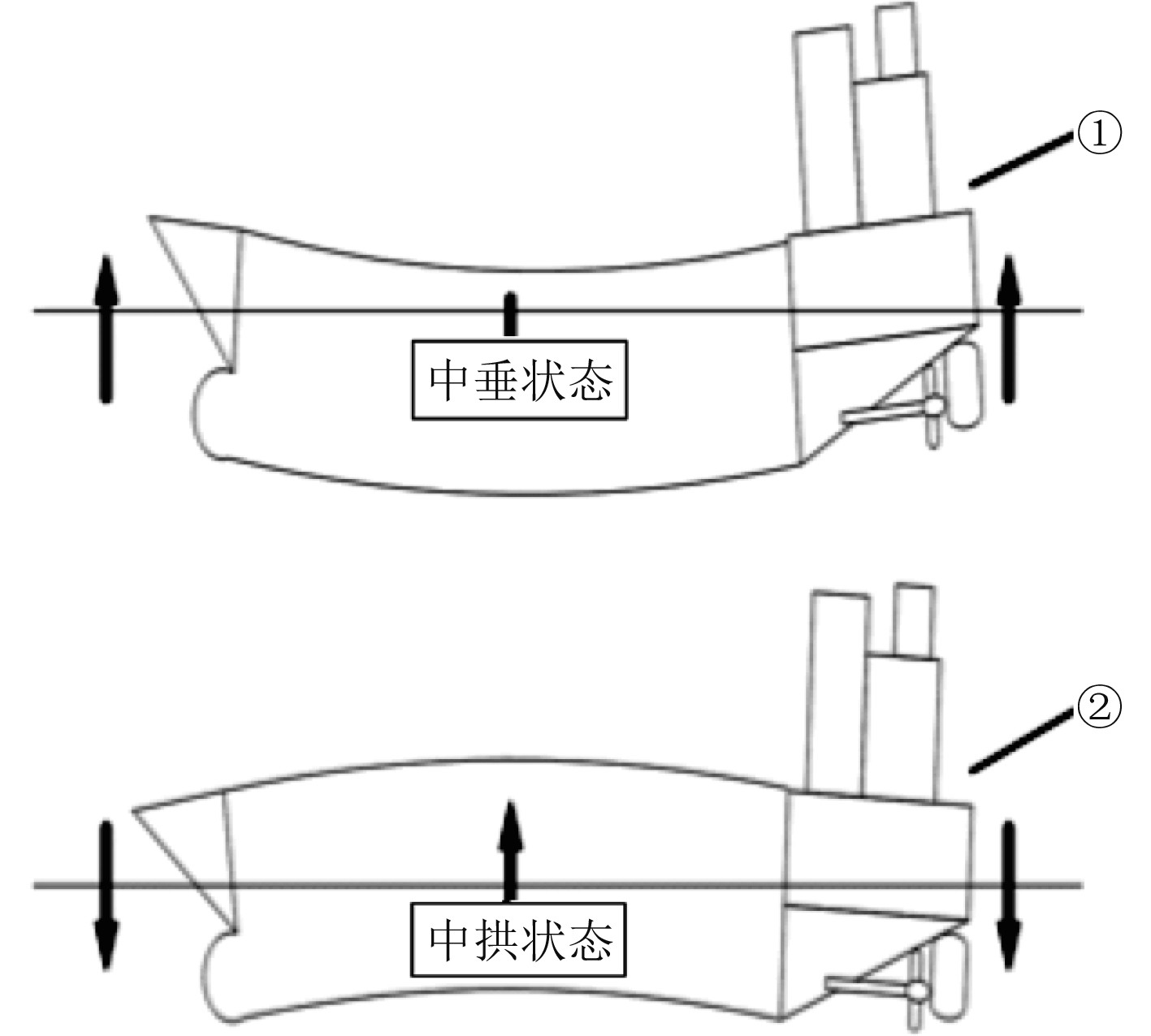
使用Solid Works2018软件建立有限元模型,弹出窗口选择OptiSruct模块,在其左侧菜单中点击OptiSruct创建分析文件,然后进行求解计算,求解结束在弹出窗口中点击results,弹出软件界面,得到4种工况应力和位移分布图,破冰船最大垂向力的工况如图2所示。
|
图 2 破冰船最大垂向力工况 Fig. 2 Maximum vertical force working condition of icebreaker |
本文基于强度理论,经计算后,得出其中中垂状态的最大垂向应力为168 MPa,应力集中在破冰船两侧处,工程中对破冰船分析时通常取安全系数为1.5,对应轮毂轴管处的许用应力为180 MPa,最大垂向力的工况下破冰船的最大应力小于该处材料的许用应力,强度合格。最大垂向力工况的最大变形量为2.230 mm,轮距变形量为1.42 mm/m,满足国家标准的小于1.5 mm/m,刚度合格。
3 破冰船强度模态计算 3.1 模态分析原理根据结构动力学,模态参数可以对振动特性进行描述,前提就是得到对应结构的固有频率和固有振型。在对该破冰船进行各项动力学分析之前,都会先进行模态分析。其目的是为破冰船的设计和改良提供强有力的数据支撑。
模态分析从原理上,一般都会对线性定常系统微分方程组设置一个物理坐标系,只要将其模态坐标进行归一化后,结构方程就具有可解耦性,这样就可以建立一组以模态坐标、模态参数作为描述对象的独立方程。由此,按照以上研究思路可以获得该系统的模态参数。
对于一个具有N自由度的线性系统,可描述其运动方程为:
| $ {\boldsymbol{M}}X+{\boldsymbol{C}}X+{\boldsymbol{K}}X=F(t)。$ |
式中:M、C、K分别为系统的质量矩阵、阻尼矩阵以及刚度矩阵;{X}为系统加速度响应;{F(t)}为系统的外部受力向量。
而无论是实对称矩阵还是非对称矩阵,在本研究中都可视为同类型的解耦方程。同时,将物理坐标相对应的模态坐标进行替代,并解耦微分方程,将其转化成一个独立的微分方程,最后进行模态分析。如果出现对角化这种特殊情况,就需要在系统的阻尼矩阵之中进行简化,得到简化后的方程为:
| $ {\boldsymbol{M}}{\ddot u} + {\boldsymbol{K}} u = {F\left( t \right)} \text{,} $ |
当系统不受到外力作用时,即上式的右端为零,如果对系统再次进行简化,阻尼为零的多自由度状态下,可以将振动方程进行如下表示:
| $ \tilde y = {\alpha _0} + \sum\limits_{j = 1}^n {{\alpha _j}{x_j}} + \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\alpha _{jj}}{x_i}{x_j}} }。$ |
假设破冰船强度受到外界振动的干扰,其振动函数为:
| $ K - {w^2} M \left\{ \Phi \right\} = 0 。$ |
最终,得到破冰船的结构刚度矩阵K,以及结构的质量矩阵M,2个矩阵都为n阶方阵,因此上式存在n个解,可知结构的n阶固有频率为:
| $ {w_1} \leqslant {w_2} \ldots \leqslant {w_n} \text{,} $ |
对于该结构的任意一阶固有频率,都可以利用以上推导流程求得其特征向量为:
| $ \left\{ \varPhi \right\} = {\left[ {{\varPhi _1}{\varPhi _2} \ldots {\varPhi _n}} \right]^{\rm{T}}} 。$ |
而以上所推导出来的结果,在破冰船强度计算流程上可以称为结构的固有振型。
3.2 破冰船的模态计算与分析使用OptiSruct求解器,分析频率范围内的固有频率,可设置默认的频率阶数为9阶,因为第1阶到第6阶为刚体模态,因此从第7阶开始进行研究。经整理后,得出各阶模态的频率值如图3所示。

|
图 3 各阶模态分析 Fig. 3 Modal analysis of each order |
根据图3可知,7阶到9阶段频率数据逐渐增加,因此固有频率将随着模态解析序列的增加而增加。其中,8阶、9阶的破冰船振型是与实际撞击冰层相对应的。当破冰船撞击的激振频率等于模态分析得到的固有频率时,就形成了相应的模态。
4 破冰船疲劳计算 4.1 疲劳分析的理论基础除了自身的重量外,破冰船在循环和交替负载下运行,也会导致其零件发生疲劳损坏。因此对破冰船进行疲劳分析,除了需要考虑外部的冰层因素外,对破冰船内部的零部件进行分析也非常重要。从以下4个部分对其展开分析:
1)对材料的S-N曲线进行确定。关于破冰船的疲劳设计,多是基于试验Wohler曲线或Manson-Coffin曲线展开分析。
2)疲劳载荷谱数据的处理与编制。破冰船在日常破冰过程中承受总载荷,这些载荷共同导致疲劳载荷。当负载水平发生变化时,驱动轴的负载水平发生变化,称为负载循环。考虑破冰船钢性材料的柔韧性非常重要,故而本文研究提出的应力-迟滞回环方程可以代表循环期间的整个塑性变形。
3)累计损伤理论。破冰船在破冰的过程中,会影响实际运行条件下的交流幅值周期,计算难度很大。如果使用Miner线性累积损伤理论,可以解决变幅周期中破冰船的疲劳寿命问题。
4)疲劳分析方法。该试验方法又可分为2种,第1种是高周疲劳分析法,第2种是低周疲劳试验。其中的高周疲劳又称应力疲劳,通常发生在低载荷和高频载荷下,并会因为零部件的老化和弹性变形而导致破冰船的强度受损。而低周疲劳或拉伸疲劳则往往是由于高载荷和低频载荷所致,并会对破冰船的使用寿命和塑性造成破坏。
4.2 疲劳仿真计算使用Solid Works2018软件进行疲劳仿真分析,该软件可在多种分析结果基础上进行疲劳分析。此外,Solid Works2018软件还具有全面的疲劳分析能力,可以对所有的疲劳仿真分析按照“输入-前处理-求解-后处理”的基本操作建立关联,由此完成相关计算。基于此,对其按照以下步骤进行计算分析:
定义时间载荷序列,载荷施加位置为破冰船的船头压水舱,载荷的施加形式为正弦波状态,载荷最大值为破冰船满载荷的2.5倍,得出:
| $ {F_{MAX}} = F = 2.5 \times \frac{G}{2} 。$ |
式中:FMAX为正弦波载荷的峰值;F为破冰船满载时要承受的垂直载荷。
已知破冰船的撞击强度为550 MPa,屈服强度为440 MPa,弹性模量为206000 MPa,泊松比为0.3。输入材料属性,得到破冰船材料特性S-N曲线,如图4所示。可以看出,负荷量随着额定电压的增长而线性增长。
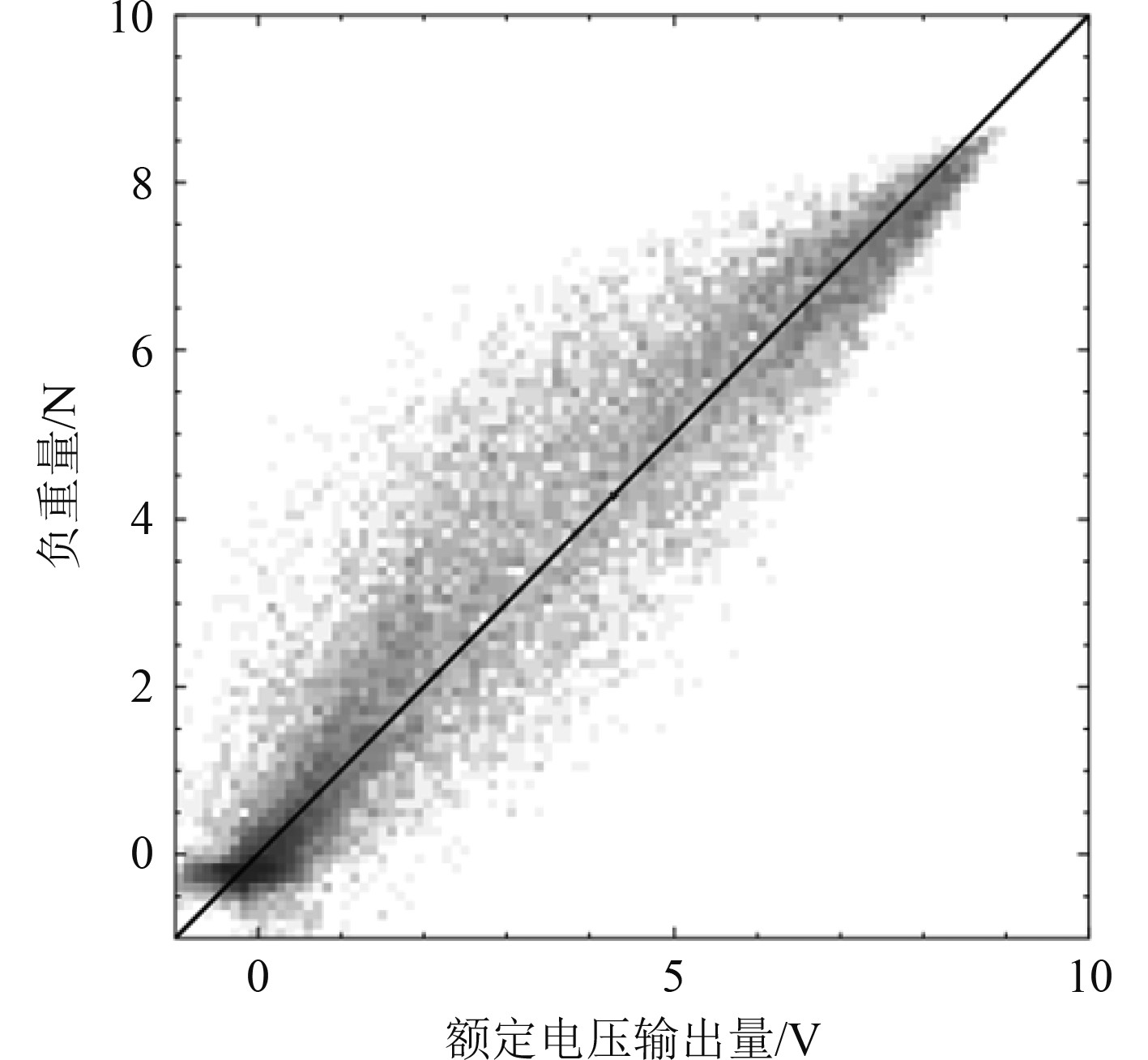
|
图 4 材料特性S-N曲线 Fig. 4 Material property S-N curve |
基于破冰船钢质材料曲线,结合材料特性S-N曲线后,按额定电压法进行分析,得到疲劳寿命最小值为破冰船撞击1.5 m厚冰层时,其平均疲劳寿命为7千次,安全系数最小值为1.2117,结果说明破冰船的疲劳寿命满足标准。
5 结 语本文基于有限元法展开的破冰船强度计算,选取破冰船的结构材质为特级钢,然后采用有限元模态分析法对船舶的抗疲劳强度进行了建模和仿真分析,从仿真结果看,为了满足足够的强度,需要重点提高材料的抗疲劳水平,使得最小的安全系数大于1,这样才能保证船舶的行驶安全性。
| [1] |
刘振冲, 潘传飞, 王丽芸, 等. 破冰船首部与侧部接触加载工况下海冰弯曲破碎过程[J]. 船舶, 2023, 34(3): 107-114. LIU Zhen-chong, PAN Chuan-fei, WANG Li-yun, et al. Bending and crushing process of sea ice under icebreaker bow and side contact loading[J]. Ships, 2023, 34(3): 107-114. |
| [2] |
赵伟栋, 冯国庆, 陈占阳, 等. 基于断裂力学的破冰船结构疲劳损伤评估方法[J]. 中国造船, 2023, 64(3): 56-67. |
| [3] |
杨薛航, 王燕舞, 李鹏飞, 等. 冰载荷作用下舷侧骨架典型节点有限元分析[J]. 中国舰船研究, 2021, 16(5): 71-77. YANG Xue-hang, WANG Yan-wu, LI Peng-fei, et al. Finite element analysis of typical joints of side frame under ice load[J]. China Ship Research, 2021, 16(5): 71-77. |
| [4] |
董一洋, 刘俊, 吴刚, 等. 破冰船冲撞式破冰模拟及结构损伤分析[J]. 船舶工程, 2020, 42(4): 26-31+136. DONG Yi-yang, LIU Jun, WU Gang, etc. Icebreaker Impact Ice Breaking Simulation and Structural Damage Analysis[J]. Ship Engineering, 2020, 42(4): 26-31+136. |
| [5] |
任奕舟, 邹早建. 破冰船在冰层中连续破冰时的冰阻力预报[J]. 上海交通大学学报, 2016, 50(8): 1152-1157. REN Yi-zhou, ZOU Zao-jian. Ice Resistance Prediction of Icebreaker Continuously Breaking Ice[J]. Journal of Shanghai Jiaotong University, 2016, 50(8): 1152-1157. |
| [6] |
程海涛, 郝用兴, 杨松伟, 等. 基于切槽与船体施压破冰的模拟分析[J]. 华北水利水电学院学报, 2013, 34(2): 107-110. |
 2023, Vol. 45
2023, Vol. 45
