概念设计阶段的船型优化论证是一个复杂的非线性全局优化问题,设计变量众多,衡准指标各异,因此优化论证过程中遇到的问题较多。长期以来国内外专家在此领域做了大量研究工作。金雁等[1]改进蚁群算法进行船舶主尺度优化论证;陈雅菊[2]将NSGA-II算法用于船型方案的求解,采用主成分分析方法对这些解进行综合评价,给出解集个体的排序;骆义等[3]运用阈值法对指标标准化,构建库区过闸适应性船型主尺度论证综合评价指标体系;卓宏明等[4]均匀设计与正交设计联用,提出均匀正交萤火虫算法求解多目标主尺度优化数学模型。
从研究的过程看,船型优化论证涉及到评价指标时,大量学者都采用了确定性参数参与计算。然而船舶实际营运过程中,涉及指标的参数存在诸多不确定性,这些不确定因素对评价指标的变化趋势和幅值会产生影响,优化计算选优的结果容易与实际情况产生偏差,进而可能导致最优决策方案的变化。
本文针对船型优化论证计算以及选择问题建立多目标优化模型,对计算模型进行拆解,梳理不确定性因素,通过对收集到的往年数据进行统计分析和概率模型拟合。对1艘600TEU绿色集装箱船分别采用基于NSGA-II的确定性优化方法和基于蒙特卡罗模拟的不确定性优化方法,对绿色技术应用下不确定因素对船型优化论证最优方案的影响进行研究。
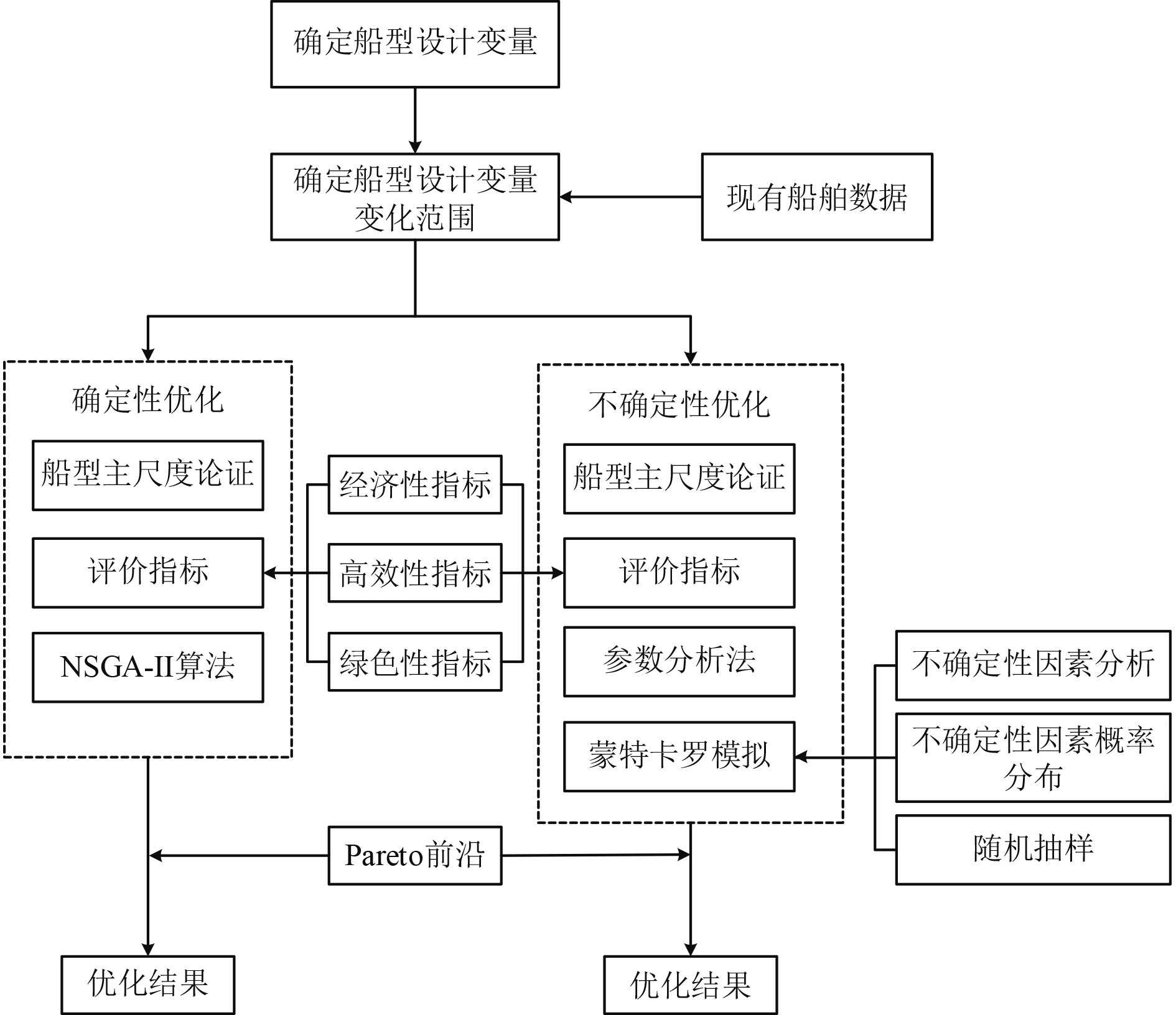
1 理论分析本文的研究思路(见图1)是将NSGA-II用于确定性优化设计,将蒙特卡罗模拟用于不确定性优化设计,对船型方案进行优化求解,通过比较2组优化结果探讨不确定性因素对船型主尺度论证的影响。
|
图 1 优化论证设计框架 Fig. 1 Optimization demonstration design framework |
假定多目标优化问题有n个优化变量,m个优化目标,则该多目标优化问题可描述为:
| $ \mathrm{min}F(x)=\left[f1(x)\text{,}f2(x)\text{,}\cdot \cdot \cdot \text{,}fm(x)\right] ,$ | (1) |
| $ {\rm{s.t.}}\{\begin{array}{c}a < x < b,\\ \begin{array}{cc}hi(x)=0& i=1\text{,}2\text{,}\cdot \cdot \cdot \text{,}I,\end{array}\\ \begin{array}{cc}gj(x)\leqslant 0& j=1\text{,}2\text{,}\cdot \cdot \cdot \text{,}J。\end{array}\end{array} $ | (2) |
式中:
对于多目标优化问题,所有满足式(2)约束的解为可行解,假定可行解集合为X。若存在解xa∈X的所有优化目标值皆优于其他可行解,则xa为最优解。然而实际情况中最优解通常不存在,因此引入Pareto解。假设存在解xb,xc∈X,解xb的所有优化目标值皆优于解xc对应的目标值,则称解xb支配xc,若X中不存在任何解支配xb,则称xb为该问题的Pareto解。
1.3 卡方检验卡方检验是一种常用的假设检验方法,其根本思想在于比较理论频数和实际频数的吻合程度或拟合优度问题[5]。具体到本文中的应用:对于收集到的不确定性因素的历史数据,假设这些数据可能服从某些概率分布,利用卡方检验法得到各种分布的拟合优度统计值,以此判断数据更接近于哪种分布。卡方检验的基本公式为:
| $ {x^2} = \sum\limits_{i = 1}^k {\frac{{{{\left( {{f_{oi}} - {f_{ei}}} \right)}^2}}}{{{f_{ei}}}}} 。$ | (3) |
式中:k为组数;
蒙特卡罗模拟是一种基于随机数的使用和概率统计问题的计算方法。在蒙特卡罗模拟中,模型参数被假定是以概率密度函数为代表的随机变量,由此产生的模型解也是随机变量;随机解的概率分布由随机参数的相互作用决定,并通过控制方程的数值实现[6]。
2 多目标优化设计数学模型 2.1 设计变量船型多目标优化论证主要确定主尺度数据,因此选取设计方案的船长L、船宽B、设计吃水T、方形系数Cb为设计变量。即
| $ x={\left\{L\text{,}B\text{,}T\text{,}{C}_{b}\right\}}^{{\rm{T}}}。$ | (4) |
从高效、经济、绿色等方面考虑,采用载重量系数、载货量/载箱量、必要运费率和能效设计指数作为优化目标函数:载重量系数最大、载货量/载箱量最大、必要运费率最小、能效设计指数最小。
2.3 约束条件除设计变量的约束外,在进行船型主尺度论证时,尺度比等需满足相关法规、规范,因此提出如下约束条件:
| $ \left\{ \begin{array}{l}L/D\leqslant 25\text{,}B/D\leqslant4,\\ 0.50\leqslant T/D\leqslant 0.85\text{,}B/T\leqslant4 。\end{array}\right. $ | (5) |
式中,D为型深。
2.4 设计模型1)目标函数1——载重量系数ηDW
| $ {\eta _{DW}} = \frac{{\Delta - LW}}{\Delta } ,$ | (6) |
式中:Δ为满载排水量;LW为空船重量。
2)目标函数2——载货量WC/载箱量CTEU:
| $\begin{split} & {W_c} = \Delta - LW - \sum {{W_i}},\\ & {C_{{\rm{TEU}}}} = [(0.8 \cdot L - {L_1} - {L_2} \cdot 2 + {L_3})/({L_{{\rm{TEU}}}} + {L_3})] \times\\ &\qquad\quad\;\; [0.8 \cdot B - {L_2} \cdot 2 + {L_3})/({B_{{\rm{TEU}}}} + {L_3})] \times 6 + {C_1} 。\end{split} $ | (7) |
式中:L1为机舱长度;L2为箱与侧壁间隙;L3为箱与箱间隙;LTEU为TEU标准箱长度;BTEU为TEU标准箱宽度;C1为非货舱区域载箱量。
3)目标函数3——必要运费率RFR
| $ RFR = \frac{{\left( {P - L} \right) \cdot \left( {A/P,i,n} \right) - L \cdot i + Y}}{Q} 。$ | (8) |
式中:L为船舶残值;(A/P,i,n)为资金回收因数;i为贷款利率;n为船舶营运年限;Q为年运输总量;Y为年营运费用;P为船舶投资。
4)目标函数4——EEDI[8]
如果不考虑锅炉的排放和使用创新能效技术减少的碳排放部分,则有:
| $ \begin{split} &EEDI = {f_j} \cdot \displaystyle\sum\limits_{i = 1}^{{n_{ME}}} {P_{ME\left( i \right)}} \times \\& \frac {\left( {S F {C_{ME\left( {{i_O}} \right)}} \cdot {C_{FME\left( {{i_O}} \right)}} \cdot \left( {1 - a} \right) + SF{C_{ME\left( {{i_O}} \right)}} \cdot R \cdot {C_{FME\left( {{i_L}} \right)}} \cdot a} \right) }{{{f_i} \cdot {f_c} \cdot Capacity \cdot {V_{ref}}}} +\\& \frac {\displaystyle\sum\limits_{i = 1}^{{n_{AE}}} {\left( {{P_{AE}} \cdot SF{C_{AE}} \cdot {C_{FAE}}} \right)} }{{{f_i} \cdot {f_c} \cdot Capacity \cdot {V_{ref}}}} 。\end{split} $ | (9) |
式中:下标为O的项为主机以柴油为燃料产生的二氧化碳的排放量,下标为L的项为主机以LNG为主燃料燃烧产生的二氧化碳的排放量;下标为ME的项表示主机,下标为AE的项表示辅机;fj为主推进装置功率修正系数;n为主(辅)机数量;P为发动机功率;SFC为燃料消耗率;CF为燃料的CO2转换系数;
通常,在进行优化时各参数均为固定值,实际上这些参数都是在一定范围内变动的。因此在进行不确定性优化时,需将参数变为不确定性参数。作为绿色船舶,采用LNG作为燃料可有效减少二氧化碳、氮氧化物的排放,使用尽可能高比例的LNG可更好发挥其绿色性,故将柴油替代率列为不确定性因素之一;在满足船舶强度、性能情况下进行结构轻量化设计,以及采用轻型高强度复合材料替代钢料,可减轻空船重量提高货船载货量,故将空船重量系数列为不确定性因素之一。在船舶全生命周期过程中,相关产品价格不仅受国家政策国际形势的影响,还受供需关系等影响,具有较大的不确定性,船价方面,将单位载重吨(载箱量)船价和绿色动力装备购置成本列为不确定性因素;燃料价格方面,将LNG价格、柴油价格列为不确定性因素。将不确定性因素加入目标函数公式进行补充,如下式:
| $ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} LW = \beta \cdot {L^{1.5}} \cdot B \cdot {D^{0.5}} \cdot \left( {1 + 0.5 \cdot {C_b}} \right),\\ P = DW \cdot {P_D} + {P_I},\\ P = {C_{TEU}} \cdot {P_D} + {P_I} ,\\ \end{gathered} \\ {Y = B \cdot a \cdot R \cdot {P_L} + B \cdot (1 - a) \cdot {P_O} + Z} 。\end{array}} \right. $ | (10) |
式中:β为空船重量系数;D为型深;DW为载重量;PD为单位载重吨(载箱量)船价;PI为绿色动力装备购置成本;B为纯柴油动力模式年耗油量;
绿色动力装备购置成本和替代率分别服从均匀分布U(50,400)(万元)和U(0.4,0.9),空船重量系数服从均匀分布U(β1-0.05,β1)(β1为根据经验公式所得值)。对于单位载重吨(载箱量)船价、油价、LNG价格,收集并分析往年数据,采用卡方检验使用多种概率分布与历史数据来做拟合,挑出拟合效果最佳的分布。
以LNG价格为例,选取国家统计局公布的2016−2021年LNG市场价格作为历史数据,历史数据拟合各种概率分布模型的拟合优度情况如表1所示。
|
|
表 1 卡方检验拟合优度值 Tab.1 Chi-square test goodness-of-fit values |
由表1可得,LNG价格与对数正态分布的拟合度相对较好,且P>0.05,可以认为LNG价格服从对数正态分布,其概率密度函数为:
| $ \left\{ \begin{array}{ll}\dfrac{1}{0.26x\sqrt{2\text{π} }}{e}^{-\frac{{\left(\mathrm{ln}x-8.21\right)}^{2}}{0.13}},& 若x > 0,\\ 0,& {\rm{others}}。\end{array}\right. $ | (11) |
采用相同方法对柴油价格、单位载重吨(载箱量)船价历史数据进行拟合,得到合适的概率分布。
3.3 基于蒙特卡罗模拟的船型论证采用参数分析法,在设计变量变化范围内构建出多个船型主尺度方案。利用Crystal Ball软件,输入目标函数模型和概率分布模型。模拟时,软件根据不确定性因素的概率分布产生一组随机数,代入目标函数模型,求得目标函数的一组子样,重复上述过程5000次。对模拟得到的一批结果进行统计分析,选用各目标函数的期望值作为该船型方案的目标函数值。对所有船型方案逐一进行蒙特卡罗模拟后求解目标函数两两之间的Pareto解。
4 实例计算 4.1 基本数据本文以1艘600TEU集装箱船的船型论证作为算例。船舶动力模式采用柴油/LNG混合动力,最大持续功率MCR=2 000 kW,柴油替代率取50%
根据长江干线集装箱船相关型船资料,考虑长江干线限制性航道条件,得到设计变量变化范围如表2所示。
|
|
表 2 设计变量范围 Tab.2 Range of design variable |
为满足600TEU集装箱船的装载要求,应对载箱量CTEU进行约束,如下式:
| $ 500 \leqslant {C_{{\rm{TEU}}}} \leqslant 700。$ | (12) |
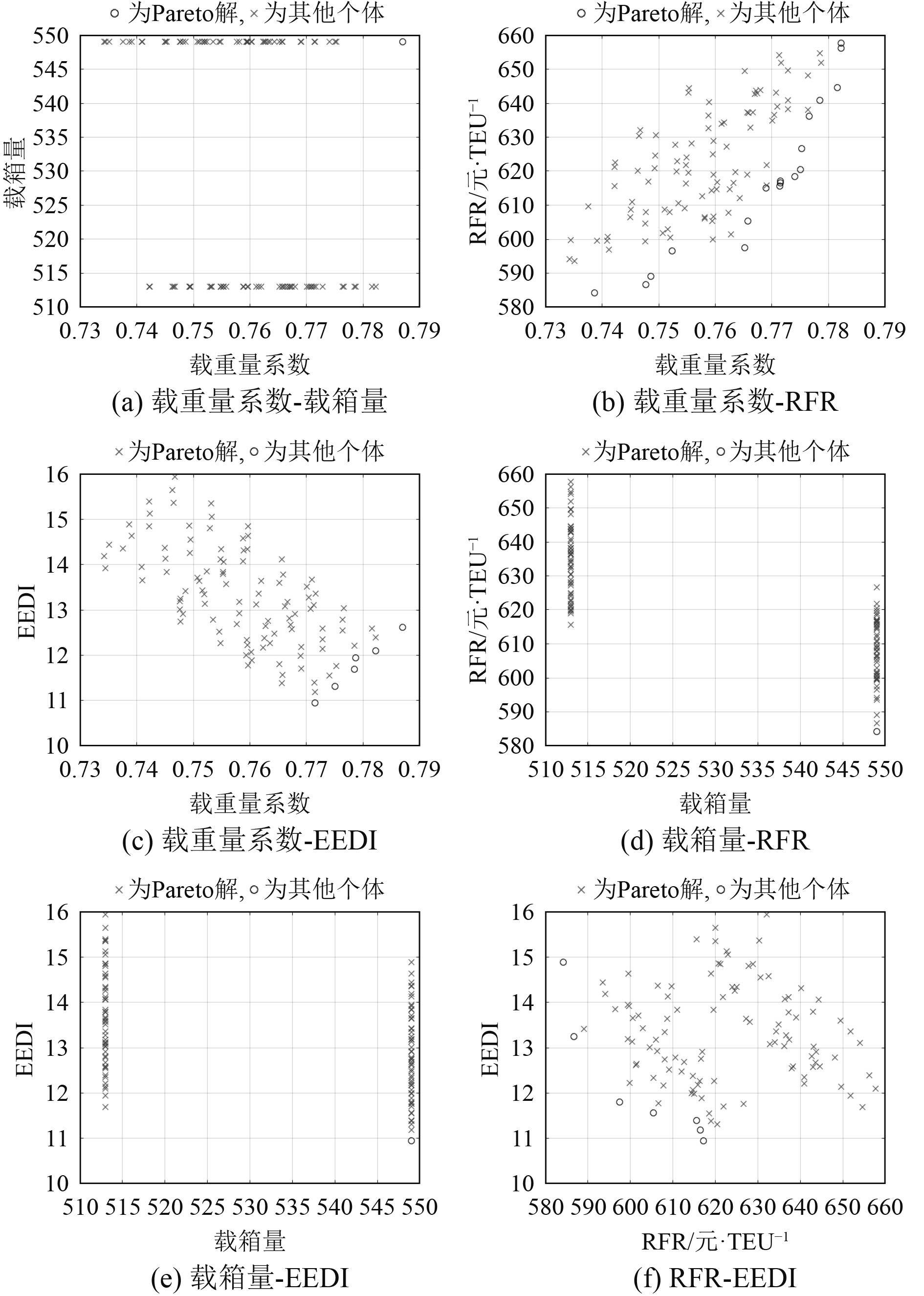
在表2变化范围内,采用参数分析法构建出多个计算船型方案。对所有船型方案进行蒙特卡罗模拟。将目标函数两两组合进行非劣解排序,得到各目标函数组合的Pareto解集如图2所示。
|
图 2 目标函数散点图及Pareto解集 Fig. 2 Objective function scatter plots and Pareto solution set |
由于TEU标准箱的布置问题,不同船型方案的载箱量可能相同,根据Pareto解集对应的设计变量值和目标函数值,各目标函数组合的Pareto解集结果中只有513TEU和549TEU两种情况。从提高集装箱船装载能力的角度出发,剔除513TEU对应的解,得到各目标函数组合的较优船型方案结果如表3所示。
|
|
表 3 各组合的不确定性优化较优船型方案 Tab.3 Optimal Solutions for Uncertainty Optimization of Each Combination |
对比目标函数组合的较优船型方案,可知:
1)各目标函数组合的较优船型方案的船长主要为变化范围中的较大值,基本都包含129 m对应船型方案。除个别方案外设计吃水基本都为5.5 m;
2)各方形系数皆有对应的较优船型方案,有研究表明,在装箱量相同的情况下,方形系数较大的船型的总油耗和单箱油耗更小[9],且有利于稳性和重箱数量的提高,故选定方形系数为0.86;
3)各船宽皆有对应的较优船型方案,相同129 m船长、5.5 m设计吃水、0.86方形系数条件下,18.7 m船宽船舶的EEDI比19.2 m船宽船舶高2.2%左右,19.6 m船宽船舶的EEDI比19.2 m船宽船舶低1.8%左右,19.2 m船宽船舶的RFR最低,三者的载重量系数和载箱量相同,19.2 m船宽船舶综合表现最优,选定船宽为19.2 m。
不确定性优化最终优化结果如表4所示。
|
|
表 4 不确定性优化最终优化结果 Tab.4 Final Result of Uncertainty Optimization |
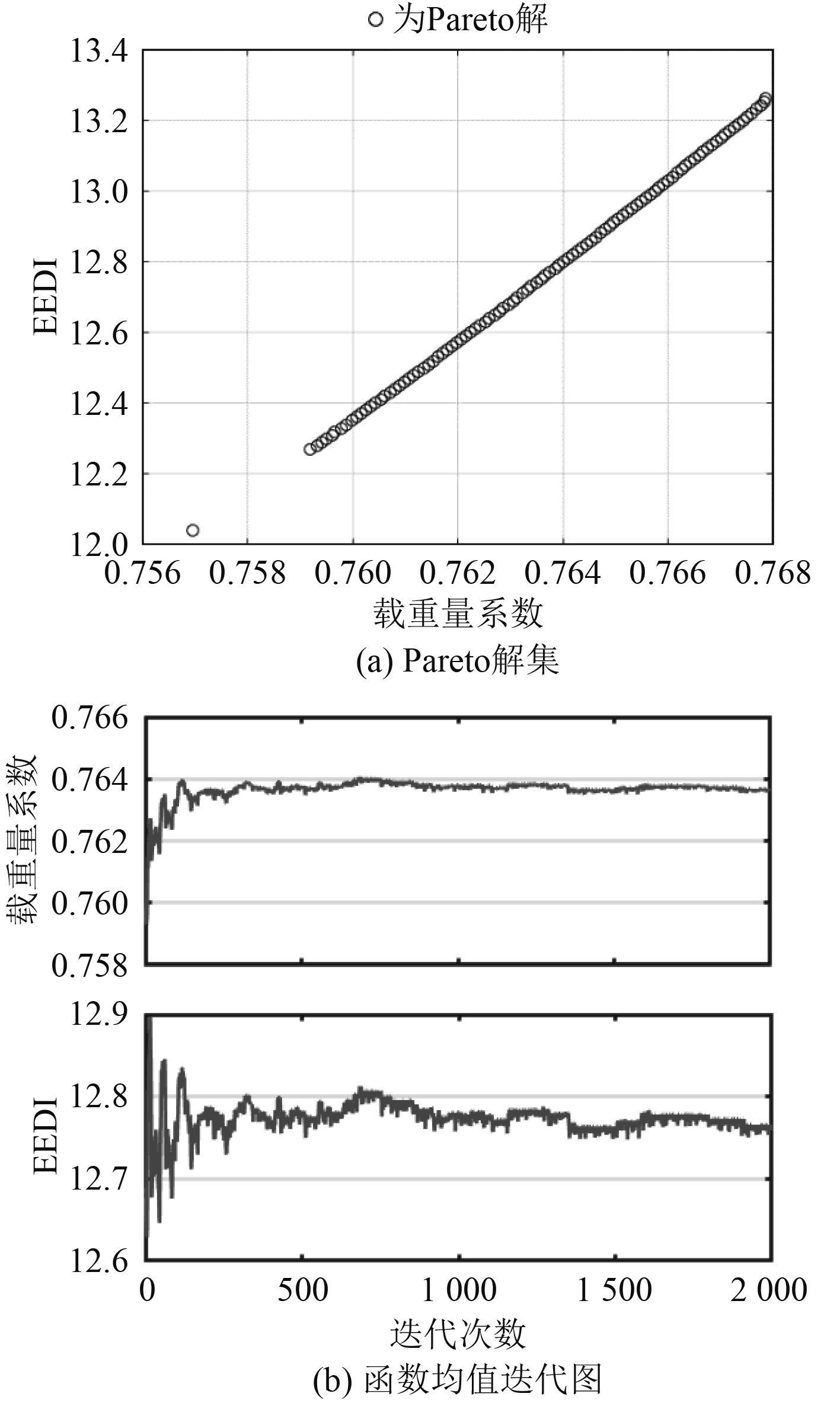
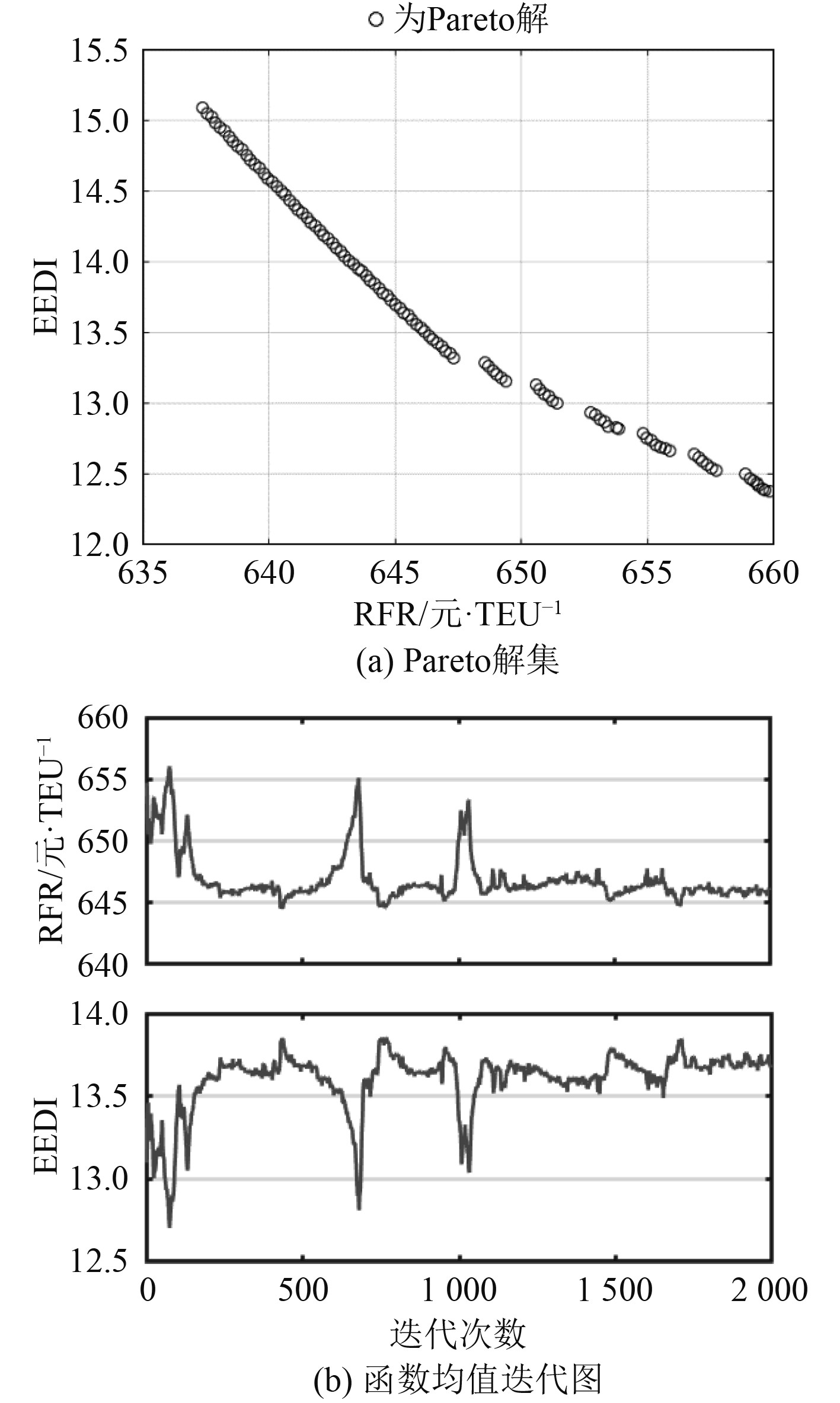
针对多目标优化模型和算例数据,利用Matlab软件实现采用NSGA-II算法的确定性优化。输入设计变量变化范围,设置算法优化参数:种群数量为100,进化代数为2000,变异概率0.2,交叉概率0.8。目标函数两两组合,在满足迭代条件后,得到排序后的最终代种群,通过平台优化计算输出各组合Pareto解集和各代Pareto解集的函数均值收敛曲线。载箱量-RFR和载箱量-EEDI组合具有最优解,故未放置输出结果图。其他组合输出结果如图3~图6所示。

|
图 3 载重量系数-载箱量 Fig. 3 Load coefficient -container capacity |

|
图 4 载重量系数-RFR Fig. 4 Load coefficient -RFR |
|
图 5 载重量系数-EEDI Fig. 5 Load coefficient -EEDI |
|
图 6 RFR-EEDI Fig. 6 RFR-EEDI |
由于TEU标准箱的布置问题,不同船型方案的载箱量可能相同,根据Pareto解集对应的设计变量值和目标函数值,各目标函数组合的Pareto解集结果中只有513TEU和549TEU两种情况。从提高集装箱船装载能力的角度出发,剔除513TEU对应的解,得到各目标函数组合的较优船型方案结果如表5所示。
|
|
表 5 各组合的确定性优化较优船型方案 Tab.5 Optimal Solutions for deterministic optimization of each combination |
对比目标函数组合的较优船型方案,可知:
1)载箱量-RFR较优船型方案的EEDI值较其他方案至少高10%,且接近船舶能效设计指数基线值RLV,排除此方案;
2)设计吃水基本相同,各目标函数组合的较优船型方案基本都包含方形系数0.86对应船型方案;
3)各较优船型方案的船长主要为变化范围中的较大值。相同船宽、设计吃水、方形系数条件下,126~133 m船长范围内,船长越大,EEDI和RFR越小,载箱量不变,载重量系数基本不变,故选定船长为较优范围内最大值133 m;
4)各较优船型方案的船宽主要分布在18.7 m和19.6 m附近。相同133 m船长、5.5 m设计吃水、0.86方形系数条件下,19.6 m船宽船舶的EEDI比18.7 m船宽船舶低3.4%左右,19.6 m船宽船舶的RFR比18.7 m船宽船舶高1.4%左右,载重量系数和载箱量相同。可从两数值中间取值以平衡各项性能,集装箱船代表船型尺度特征值[10]中19.2 m符合此要求,选定船宽为19.2 m。
确定性优化最终优化结果如表6所示。
|
|
表 6 确定性优化最终优化结果 Tab.6 Final Result of Deterministic Optimization |
针对算例中的600TEU级绿色集装箱船,本文采用了确定性和不确定性分析进行船型论证,结果对比如表7所示。
|
|
表 7 确定性优化和不确定性优化结果对比 Tab.7 Comparison of Deterministic and uncertain optimization results |
对比分析表7中各项数值,可得如下结论:
1)不确定性优化考虑了不确定性因素后,船型论证选优收敛得到的全局最优点与确定性优化论证结果相差不大,仅船长存在些微区别。说明考虑这些不确定性因素不影响船型方案的理论优化结果。
2)考虑了不确定性因素后载重量系数增加了2%左右,必要运费率降低了7%左右,EEDI降低了6%左右,表明传统的确定性论证方法低估了该船型的载重能力、盈利空间和能效水平。原因一是考虑船舶轻量化后,空船重量降低,排水量不变的前提下载重量提高;原因二是引入了不确定性分析后,各项价格由较高的价格变为一个区间范围内的波动;原因三是LNG对环境更为友好,采用了更高比例的LNG燃料后产生的柴油和LNG之间的CO2排放差值以及市场采购差价。
3)两组数据方案的EEDI情况均达到能效设计-2等级,但确定性优化的EEDI值与能效设计-2要求值仅相差0.37,若载重量发生变化极有可能降为能效设计-1等级,另外未来的碳税机制可能对EEDI值有更严格的要求。若采用确定性优化方法,航运企业可能因EEDI未达到相关要求而放弃该主尺度方案甚至放弃该吨级船型;若采用不确定性优化方法,航运企业将有较大概率选择这一优化结果。此时不确定性优化方法对船型方案选优造成影响。同理,当市场运价仅能满足不确定性优化计算得到的RFR值而不能达到确定性优化的RFR值时,不确定性优化方法对船型方案选优造成影响。
综上所述,船型论证考虑不确定性因素后,虽然不影响船型主尺度方案的理论优化结果,但不确定性优化结果的高效性、经济性和绿色性方面的目标函数值较确定性优化结果的目标函数值更优,也更贴近实际情况,可更好地为企业准确做出投资决策提供支撑。
| [1] |
金雁, 赵耀. 基于改进蚁群算法的船舶主尺度优化[J]. 华中科技大学学报(自然科学版), 2008, 11: 99-102. JIN Y, ZHAO Y. Optimization of ship principal parameters with improved ant colony algorithm[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2008, 11: 99-102. |
| [2] |
陈雅菊. 基于多目标粒子群优化和主成分聚类分析的船舶主尺度分析[J]. 舰船科学技术, 2015, 37(8): 45-51. CHEN Y J. Application of multiobjective particle swarm optimization and principle component clustering analysis in ship main dimensions analysis[J]. Ship Science and Technology, 2015, 37(8): 45-51. DOI:10.3404/j.issn.1672-7649.2015.08.010 |
| [3] |
骆义, 高惠君, 魏洪斌. 三峡库区过闸适应性船型主尺度论证[C]//中国造船工程学会. 第十二届全国内河船舶与航运学术会议论文集. 北京: 中国造船工程学会, 2012: 125–131.
|
| [4] |
卓宏明, 陈倩清. 基于均匀正交萤火虫算法的采矿船主尺度优化[J]. 船海工程, 2020, 49(5): 76-80. DOI:10.3963/j.issn.1671-7953.2020.05.018 |
| [5] |
杨朝辉. 基于卡方检验的SAR图像道路检测算法[J]. 计算机工程与设计, 2012, 33(5): 1923-1927. DOI:10.3969/j.issn.1000-7024.2012.05.050 |
| [6] |
Rubinstein R Y, Kroese D P. Simulation and the Monte Carlo method (2nd ed. )[M]. New York: John Wiley & Sons, 2007.
|
| [7] |
刘光明. 内河柴油/LNG双燃料船舶能效提升方法研究[D]. 武汉: 武汉理工大学, 2019.
|
| [8] |
中国船级社. 内河绿色船舶规范[S]. 北京: 人民交通出版社, 2020.
|
| [9] |
谷宇, 包岩, 邓强. 超大型集装箱船方形系数及载箱量优选研究[J]. 船舶工程, 2017, 39(8): 21-24+68. |
| [10] |
JTS180-4-2020, 长江干线通航标准[S]. 北京: 人民交通出版社, 2020.
|
| [11] |
张仁颐. 船舶工程经济学[M]. 上海: 上海交通大学出版社, 2001: 205–208.
|
| [12] |
HOU Y H, Kang K, Xiong Y P, et al. Uncertainty optimisation design of USV based on the Six Sigma method[J]. Ocean Engineering, 2020, 200: 107045. DOI:10.1016/j.oceaneng.2020.107045 |
| [13] |
苏绍娟, 介推, 刘波. 基于阻力和EEDI的船舶主尺度要素多学科设计优化[J]. 上海海事大学学报, 2018, 39(1): 25-30. SU S J, JIE T, LIU B. Multidisciplinary optimization design on ship principal dimensions based on resistance and EEDI[J]. Journal of Shanghai Maritime University, 2018, 39(1): 25-30. |
 2023, Vol. 45
2023, Vol. 45
