0 引　言

大型水面舰艇是执行海上军事任务的主力军，是海上国防力量建设最重要的组成部分；出色的制海、制空及对岸攻击能力使水面舰艇成为重要的作战装备，具有良好的战略威慑作用。然而，水面舰艇的目标庞大，是敌方首要攻击的目标，舰艇面临着越来越严酷的爆炸与冲击环境威胁。为保证舰船具有足够的安全性和战斗力，舰船的结构要具有一定的水下抗爆抗冲击能力。

近年来，国内外越来越多的学者对水下爆炸结构毁伤力学机理进行了一系列的系统研究^[1-2]，但主要针对舰船结构在爆炸载荷作用下的能量分布规律及能量耗散机理研究却很少。目前对船舶结构能量分布及耗散机理在船舶碰撞领域有少量的研究成果。

邱晓清等^[3]运用数值和试验的方法针对冲击波和破片联合对结构的抗侵彻能力和破坏模式进行了研究。李樱等^[4]采用任意拉格朗日—欧拉法研究水下近场与接触爆炸船体舱段的毁伤特性，研究该方法的可靠性及破口大小与结构的毁伤模式。赵松涛等^[5]基于普通拉格朗日—欧拉法建立了近自由面水下爆炸流固耦合计算模型，对舰船结构及燃气轮机冲击损伤特性进行了评估分析。姚琪等^[6]使用数值仿真软件LS-DYNA研究了船底结构搁浅变形能和船舶结构的抗搁浅能力。福萍^[7]总结了目前海洋平台的碰撞分析方法，重点研究了两端固支薄壁钢管在侧向载荷作用下的损伤变形特征和吸能特性。陈美霞等^[8]、伍星星等^[9]分别研究了偏心加筋板中弯曲波的传递特征及水下近距离爆炸对舷侧毁伤的试验，分析了爆炸对水上舰船的损坏效应。

以上能量传播与耗散研究主要集中在船舶碰撞与搁浅领域以及简单的板架结构能量传递原理，针对水下近场爆炸载荷作用下船底分段的能量传播及耗散机理国内研究较少。本文基于CEL耦合法研究水下近距离不同炸药量下，舰船底部分段结构的能量分布及能量耗散，给出了水下近距离爆炸载荷作用下船底分段结构的数值计算方法。

1 数值计算方法 1.1 方法介绍

由于双重渐进法程序(DAA) ^[11]一般被用来求解远场爆炸的结构响应，计算流体动力学程序(CFD) ^[10]在计算结构响应方面基本不具有优势。因此本文使用爆炸流体动力学程序(HYDROCODES)^[12]中普通拉格朗日欧拉(CEL)格式对水下爆炸进行数值模拟计算，采用一般耦合方法模拟水下爆炸与多物质接触面问题。

在研究爆炸力学时控制方程一般使用能够守恒型，因此得到的方程差分形式具有守恒性。假设方程的介质在直角坐标系中是连续的、均匀的、各向同性的。可以推导出3大基本方程的守恒形式，其通用形式为^[12]：

$ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} + \frac{{\partial H}}{{\partial z}} = J 。$

(1)

其中， $ U $ 、 $ F $ 、 $ {G} $ 、 $ H $ 及 $ J $ 为列向量。

$ \begin{split} &U = \left\{ \begin{gathered} \rho \\ \rho u \\ \rho v \\ \rho w \\ e \\ \end{gathered} \right.,\;\;\;F = \left\{ \begin{gathered} \rho u \\ \rho {u^2} + p \\ \rho vu \\ \rho wu \\ (e + p)u \\ \end{gathered} \right.,\;\;\;G = \left\{ \begin{gathered} \rho v \\ \rho uv \\ \rho {v^2} + p \\ \rho wv \\ (e + p)v \\ \end{gathered} \right. ，\\ & H = \left\{ \begin{gathered} \rho w \\ \rho uw \\ \rho vw \\ \rho {w^2} + p \\ (e + p)w \\ \end{gathered} \right.,\;\;\;J = \left\{ \begin{gathered} 0 \\ \rho {f_x} \\ \rho {f_y} \\ \rho {f_z} \\ \rho (u{f_x} + v{f_y} + w{f_z}) \\ \end{gathered} \right. \end{split} $

(2)

式中：t为时间；ρ为密度； $ (x,y,z) $ 为3个方向的坐标；p为压力； $ (u,v,w) $ 为 $ (x,y,z) $ 方向的速度； $ e $ 为单位体积总能量。

方程数为5个，未知物理量为6个： $ \rho ,u,v,w,p $ 及e。对此动力学问题的求解需补充给出 $ p $ 和 $ \rho $ ， $ e $ 之间关系的状态方程。在模拟近距离爆炸的过程中，对所涉及的材料选取恰当的状态方程，确保模拟结果的准确度。

1) 炸药状态方程

采用TNT炸药，并模拟因炸药爆炸产生空气压力对模型冲击的过程，对炸药采用JWL状态方程：

$ p = A(1 - \frac{\omega }{{{R_1}\bar V}}){e^{ - {R_1}\bar V}} + B(1 - \frac{\omega }{{{R_2}\bar V}}){e^{ - {R_2}\bar V}} + \frac{{\omega E}}{{\bar V}}。$

(3)

式中： $ p $ 为压力， $ E $ 为初始内能； $ \overline V $ 为比容； $ A $ =3.7375×10⁸ kPa， $ B $ =3.7471×10⁶ kPa， $ {R_1} $ =4.151， $ {R_2} $ =0.91， $ \omega $ =0.352， $ {E_0} $ =6.01×10⁶ kJ/m³， $ {\overline V _0}{\text{ = 1}}{\text{.0}} $ 。当炸药膨胀到一定的体积时，状态方程右端的前两项可忽略，此时可用理想气体的状态方程模拟炸药的行为： $p = \rho (\gamma - 1)e$ ，其中 $ \gamma = \omega + 1 $ 。

2) 水的状态方程

水的多项式状态方程由下式给出：

$ \left\{ \begin{gathered} p = {a_1}\mu + {a_2}{\mu ^2} + {a_3}{\mu ^3} + ({b_0} + {b_1}\mu + {b_2}{\mu ^2}){\rho _0}e，\;\;\;\;\;\mu > 0 ，\\ p = {a_1}\mu + ({b_0} + {b_1}\mu ){\rho _0}e，\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu < 0。\\ \end{gathered} \right. $

(4)

式中： $ {a_1},{a_2},{a_3},{b_1},{b_2},{b_3} $ 是物态方程经验系数； $ \mu $ ， $ e $ 与前面相同。而Gruneisen系数表示为，

$ {\gamma _G}{\text{ = (}}{b_0} + {b_1}\mu + {b_2}{\mu ^2}{\text{)/(}}\mu + 1{\text{)}}，$

(5)

$ {c^2} = \frac{1}{{{\rho _0}}}[{a_1} + 2{a_2}\mu + 3{a_3}{\mu ^2} + ({b_1} + 2{b_2}\mu ){\rho _0}e] + \frac{{p(\mu ,{\rho _0}e)}}{{{\rho _0}(\mu + 1)}}{\gamma _G}(\mu ) 。$

(6)

3) 空气的状态方程

计算需对空气进行模拟，空气采用理想气体状态方程为：

$ p = \rho (\gamma - 1)e。$

(7)

其中： $ \rho $ =1.2351×10⁻³g/cm³；比内能 $ e $ =2.067752×10⁵kJ/kg；绝热指数 $ \gamma $ =1.4。

4) 金属材料本构模型

金属材料采用J-C本构模型，其具体的表现形式为：

$ {\sigma _Y}{\text{ = (}}A{\text{ + }}B\varepsilon _p^* )\left[1 + C{\text{ln}}\left(\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}\right)\right](1 - {T^{*m}}{\text{)}} ，$

(8)

$ {T^*}{\text{ = (}}T{{ - }}{T_r}{\text{)/(}}{T_m}{{ - }}{T_r}{\text{)}}。$

(9)

式中： $ {\sigma _Y} $ 为动态屈服应力； $ A $ 为静态屈服应力； $ B $ 为硬化参数； $ \varepsilon _p^* $ 为有效塑性应变； $ n $ 为硬化指数； $ C $ 为应变率参数； $ \dot \varepsilon $ 为有效塑性应变率； $ {\dot \varepsilon _0} $ 为参考应变率，一般取 ${\dot \varepsilon _0}{\text{ = }}1\;{{\text{s}}^{{{ - 1}}}}$ ； $ T $ 为温度； $ {T_r} $ 为室温； $ {T_m} $ 为融化温度； $ m $ 为温度指数。

1.2 数值模拟结果分析

使用LS-DYNA模拟104.32 kg炸药在边长为8 m的立方体空气域中心爆炸所产生的冲击波对模型的冲击情况，如图1(a)所示。因为本次计算模型具有对称性，所以使用1/8模型计算结果模拟整个模型，使用正六面体实体单元SOLID164对模型进行网格划分。为确保计算的精度，靠近炸药附近的网格划分较细，远离炸药部分的网格则相对粗一点，并在有限元模型上设置对称的边界条件，具体如图1(b)所示。

炸药爆炸产生的冲击波在无限空气域中传播，对模型产生的冲击压力云图如图2所示。使用映射技术可从1/8模型的压力分布反映出整个模型的冲击压力云图。

模型中某单元在不同爆炸距离下的单元应力随时间变化历程图如图3所示。可以看出，爆炸产生的空气压力幅值随爆炸距离的增大而逐渐变小，且减小的幅度逐渐变小；空气压力在无限远处趋近于大气压强，爆炸距离越远，空气压力达到峰值所需的时间越长。

经过数值模拟计算得到相同炸药质量在不同爆炸距离下产生的冲击压力结果与经验公式计算结果进行对比，如表1所示。本次数值模拟结果取自爆炸冲击压力峰值时模型中某一单元的平均压力值，不是精确到爆炸距离的准确压力结果，具有一定的误差性，误差与单元的尺寸大小成正比关系。对比分析表1可知，在爆炸距离为1.40 m时数值结果与经验公式结果较为吻合，相对误差较小。但随着爆炸距离增大或者减小，两者之间的相对误差则明显增大，由此可知数值模拟与经验公式计算的结果存在一定的局限性，对爆炸距离比较敏感。

将经验公式计算所得到的结果与数值模拟不同爆距相同炸药质量产生的冲击波压力结果进行对比分析，如表1所示。

本次模拟的钢板与爆炸载荷均具有对称性，因此只建立模型的1/4，使用SOLID164单元划分模型，钢板的材料参数如表2所示。

数值模型中设置长、宽为70 mm、高为200 mm的计算域，炸药包共有3个不同的爆炸位置，钢板、炸药及空气域的结构如图4所示。模拟1.3 m、1.4 m和1.5 m等爆距下炸药爆炸对钢板产生的变形结果，并将数值模拟结果与试验结果进行对比，如图5所示，自上而下的钢板爆距依次为1.3 m、1.4 m和1.5 m。经过对比2种计算结果具有高度的一致性，验证本次数值模拟方法是正确的，结果可靠。

2 船底板架结构能量及应力分析 2.1 船底板架结构能量分析

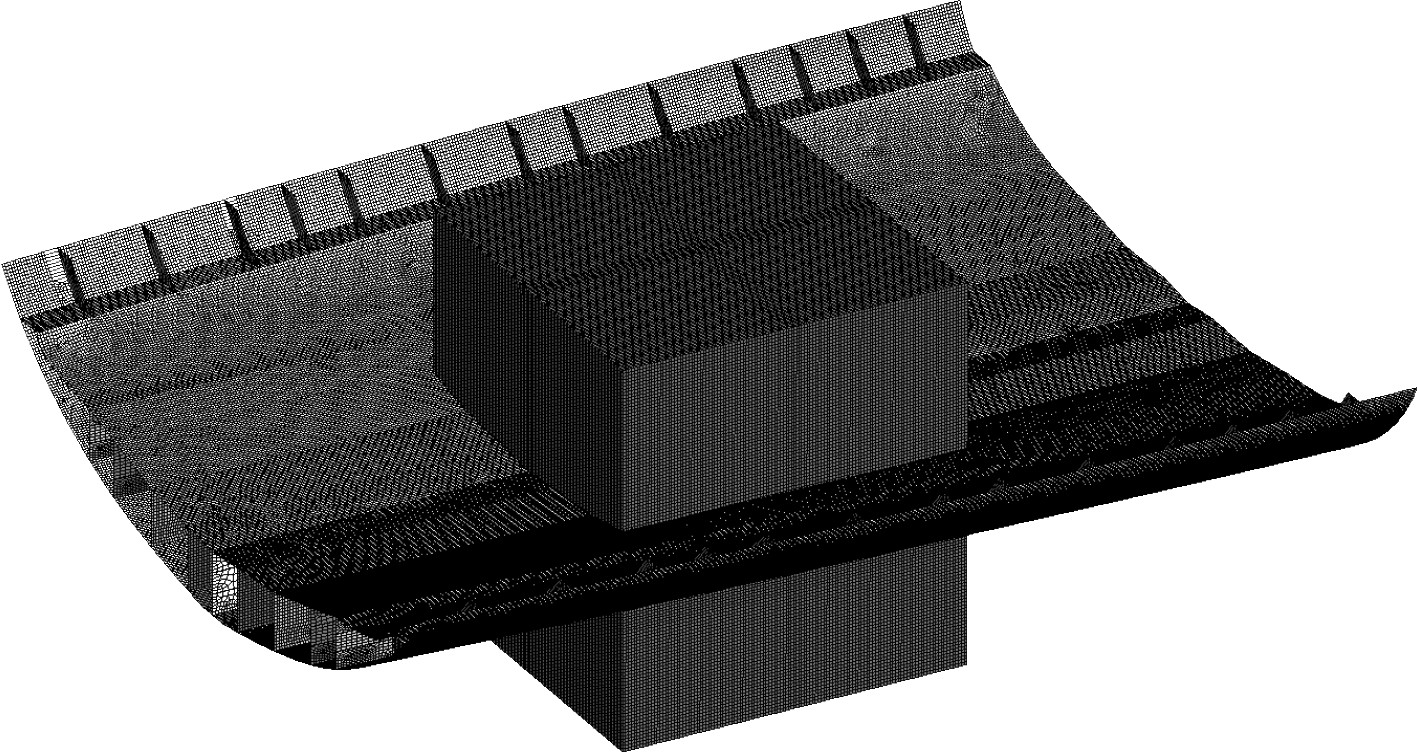
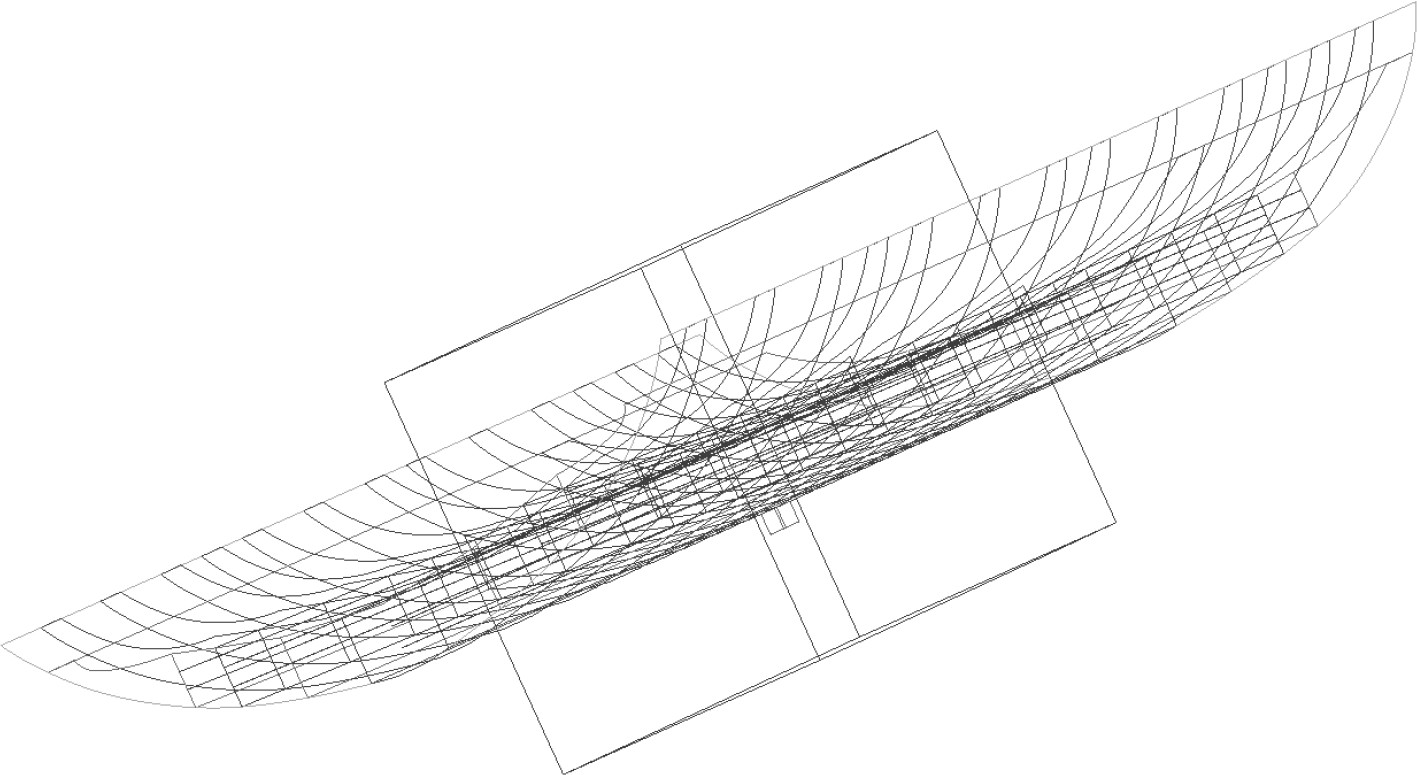
船底部分段有限元模型及欧拉域的有限元模型分别如图6所示。为控制边界条件对计算结果的影响，将边界压力值设置为大气压力，边界条件设置为自由流入且无反射流边界。同时将欧拉体网格划分为质量较好的六面体网格，TNT的装药形状设置为立方体，TNT药包与底部舱段的位置如图7所示。药包分别设置为500 kg、1000 kg、1500 kg和200 kg等不同的质量，并将其放在底部分段的中心位置。

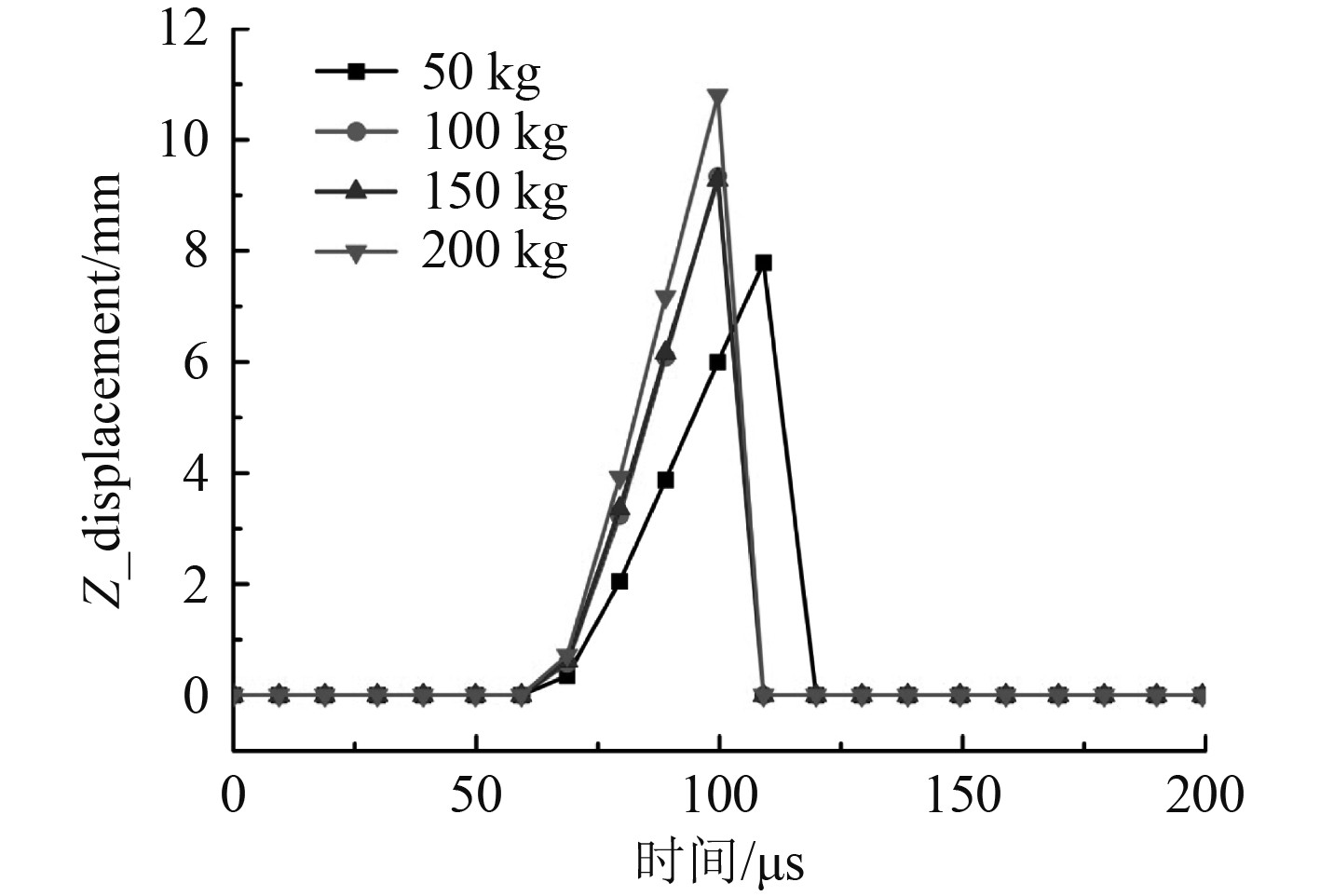
不同炸药爆炸产生的冲击波对船底板中心点的冲击变形程度如图8所示。可以看出，在炸药位置相同情况下，随着炸药量逐渐变大，结构的塑性变形程度也随之增大；100 kg、150 kg和200 kg 3种工况下船底分段中部结构失效的时间点基本一致，均在100 μs附近，而50 kg炸药量工况时失效时间点稍稍偏后，在110 μs附近。主要原因是50 kg时炸药量小，冲击波的压力小，导致失效时间偏后。

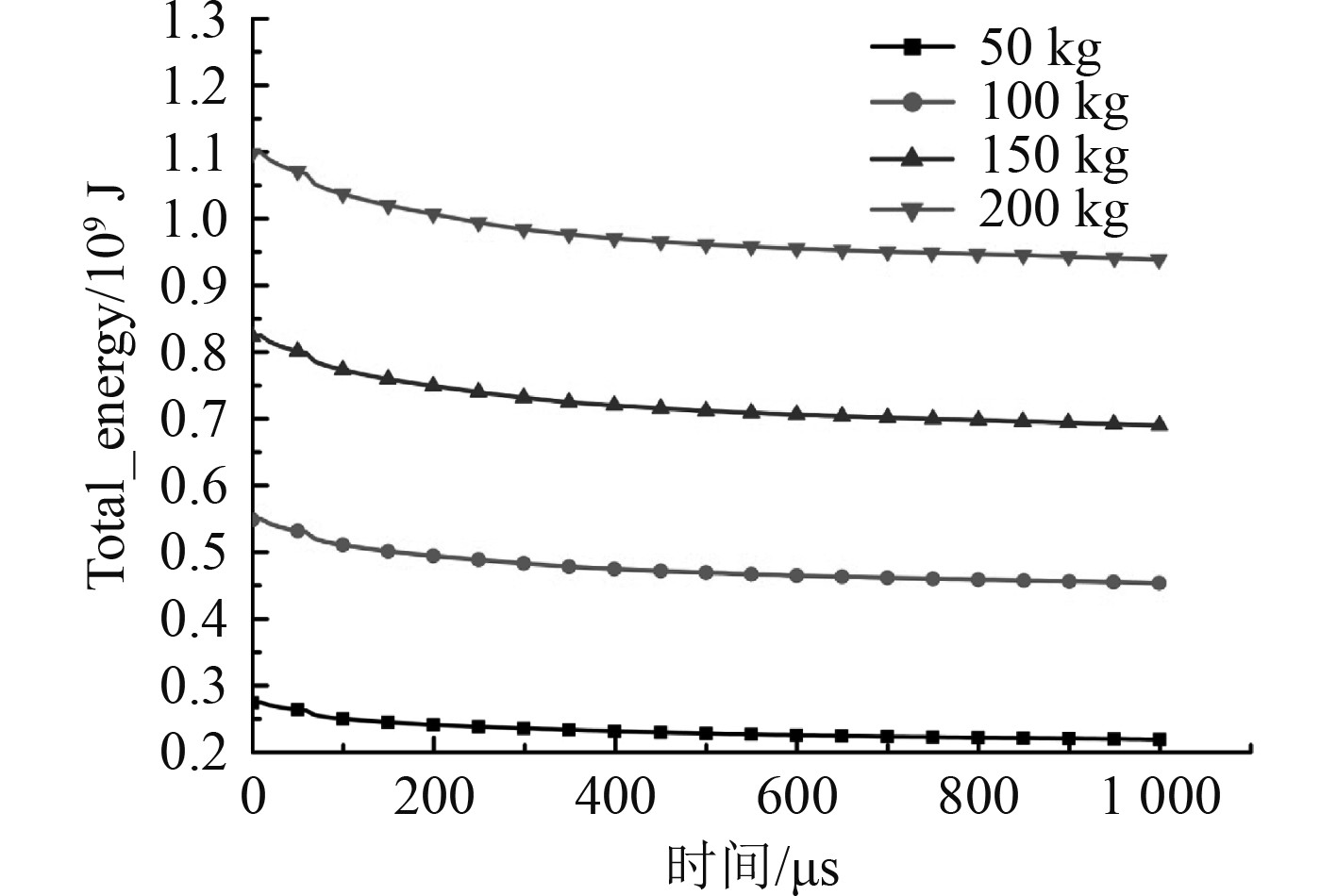
4种炸药量作用下船底分段结构和炸药的总能量历程如图9所示。可知，初始阶段船底分段结构能量为0，主要是炸药储存的能量，随着爆炸的进行，炸药的能量一部分传递给船底分段结构，一部分通过热量或其他形式耗散掉了。炸药的能量与炸药的质量是成正比的，随着时间的增加4种工况下炸药耗散的能量基本相同，因此作用到船底分段结构的能量与炸药量呈正比的关系。

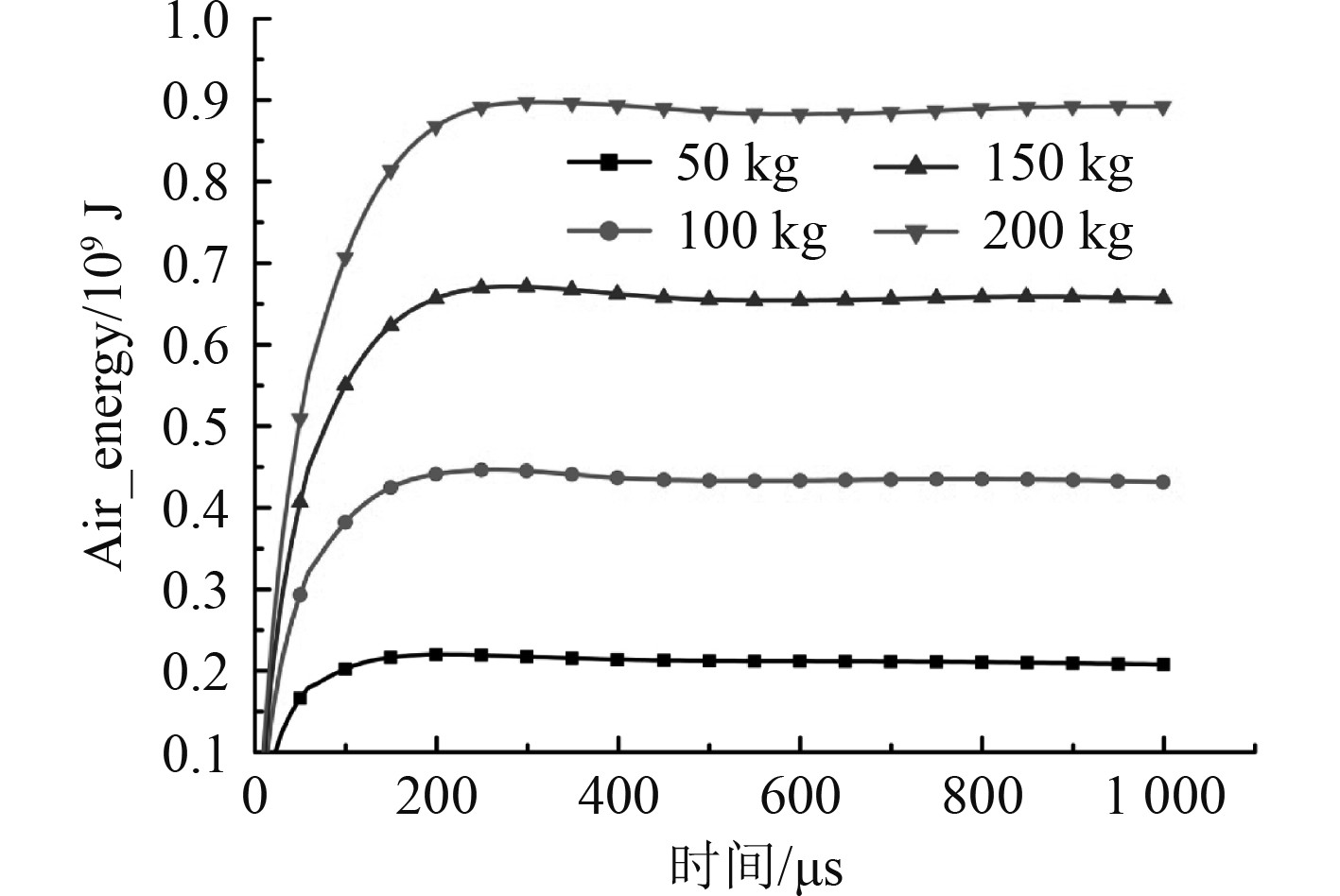
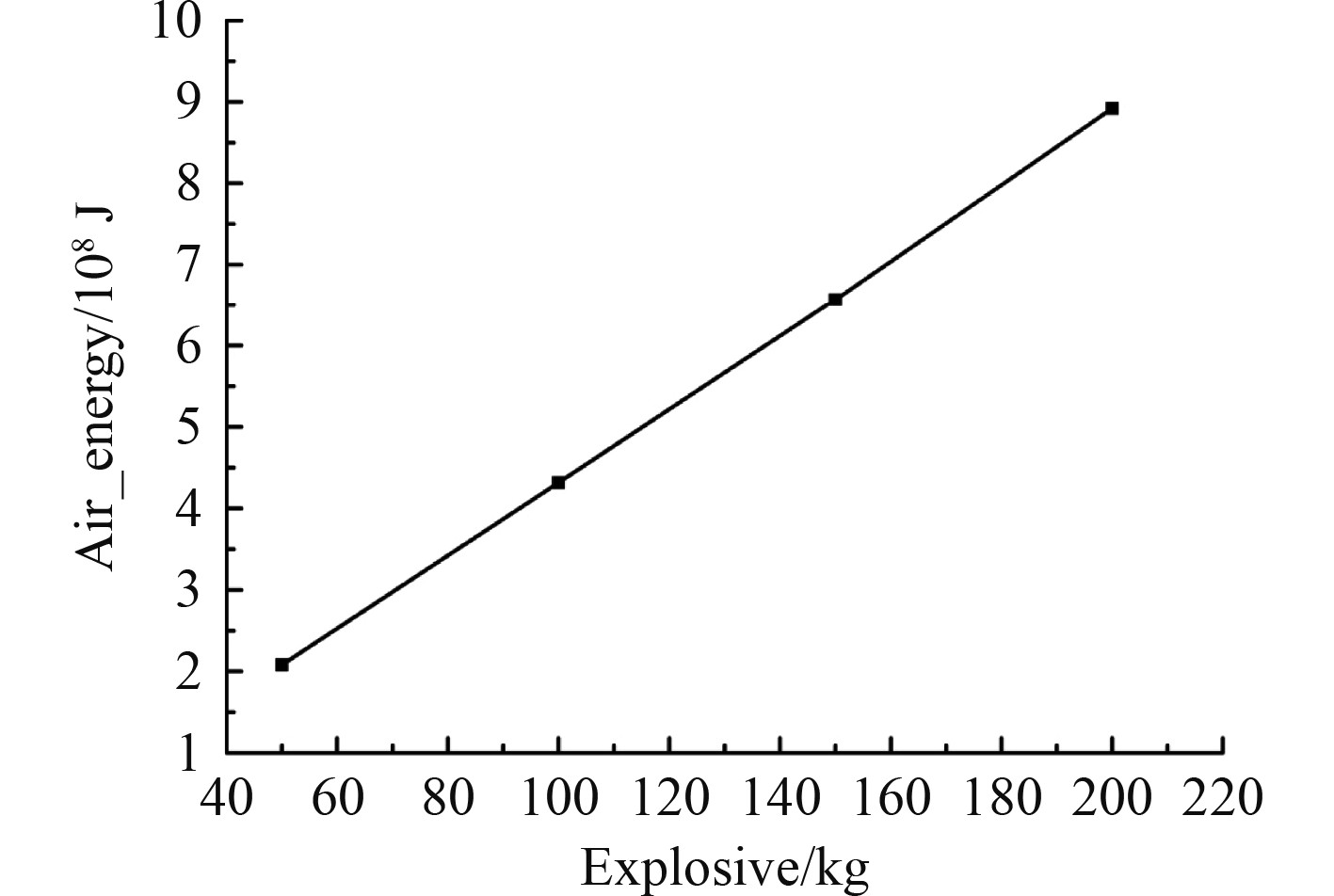
4种炸药量下耗散到空气中的能量如图10所示。可知，4种炸药量下耗散到空气中的能量分别为2.079×108 J、4.317×108 J、6.568×108 J和8.921×108 J，呈严格的线性关系，如图11所示。因此可得出结论：在被爆结构相同，炸药形状大致一致时，耗散到空气中的能量与炸药的质量是严格呈线性关系。

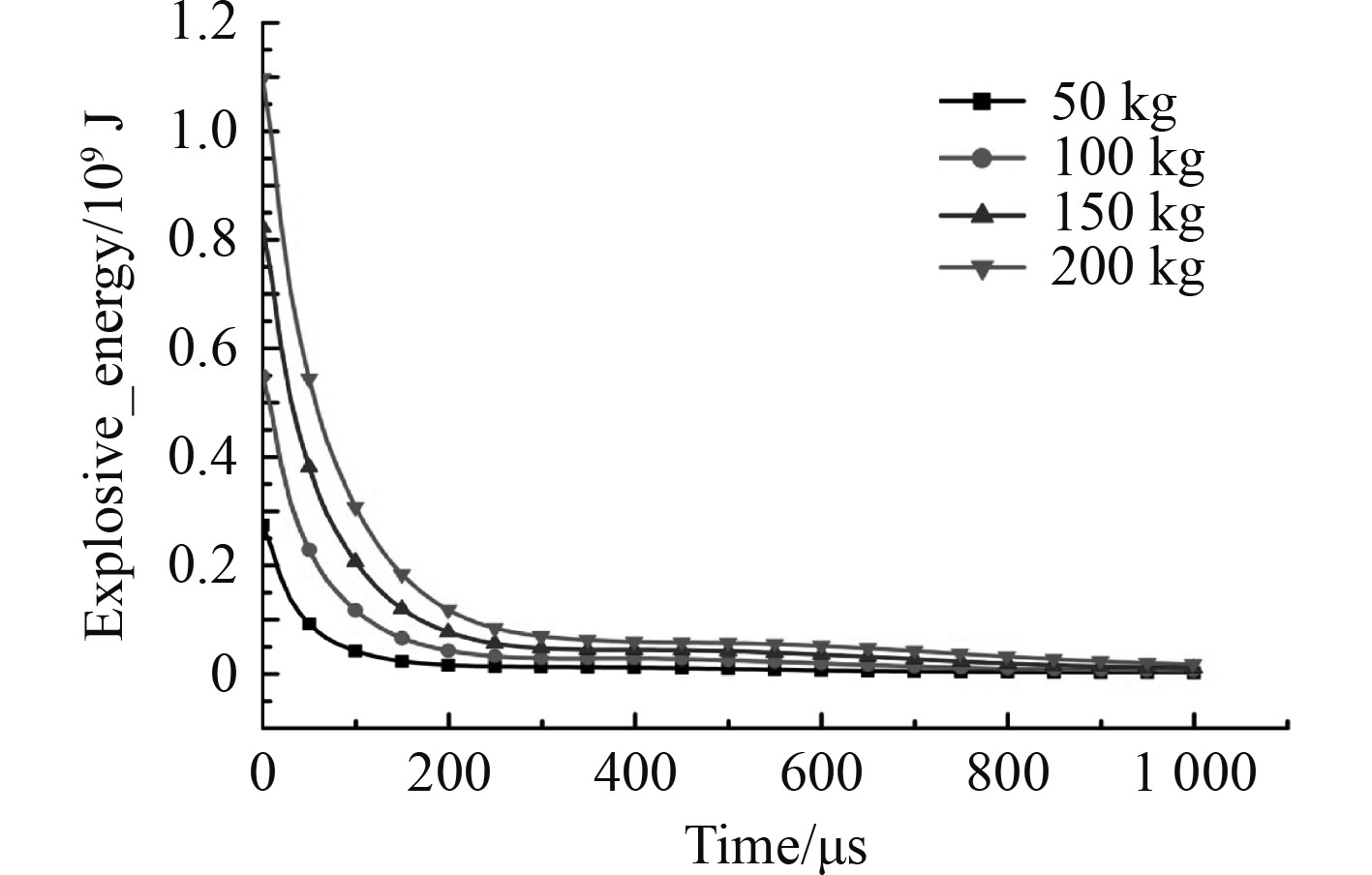
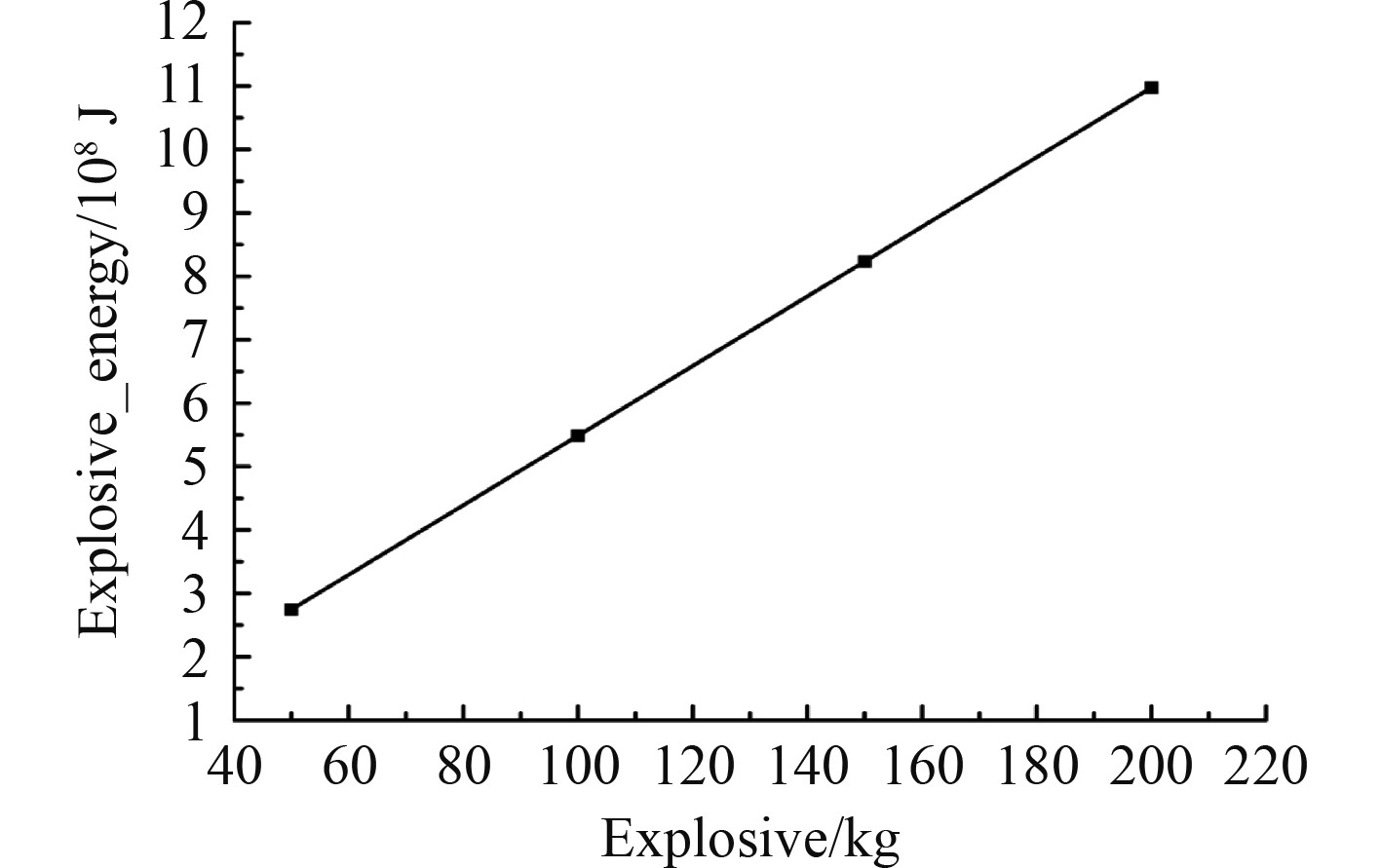
4种不同质量的药包爆炸产生的总能量及能量随时间变化的历程曲线如图12所示。可知，炸药释放能量的速度随时间的增加而逐渐递减，并且在300 μs时能量基本释放完毕。4种炸药包初始能量分别为2.744×108 J、5.488×108 J、8.234×108 J和1.098×108 J，炸药质量与炸药能量关系如图13所示。可知，炸药质量和炸药能量是严格线性关系。

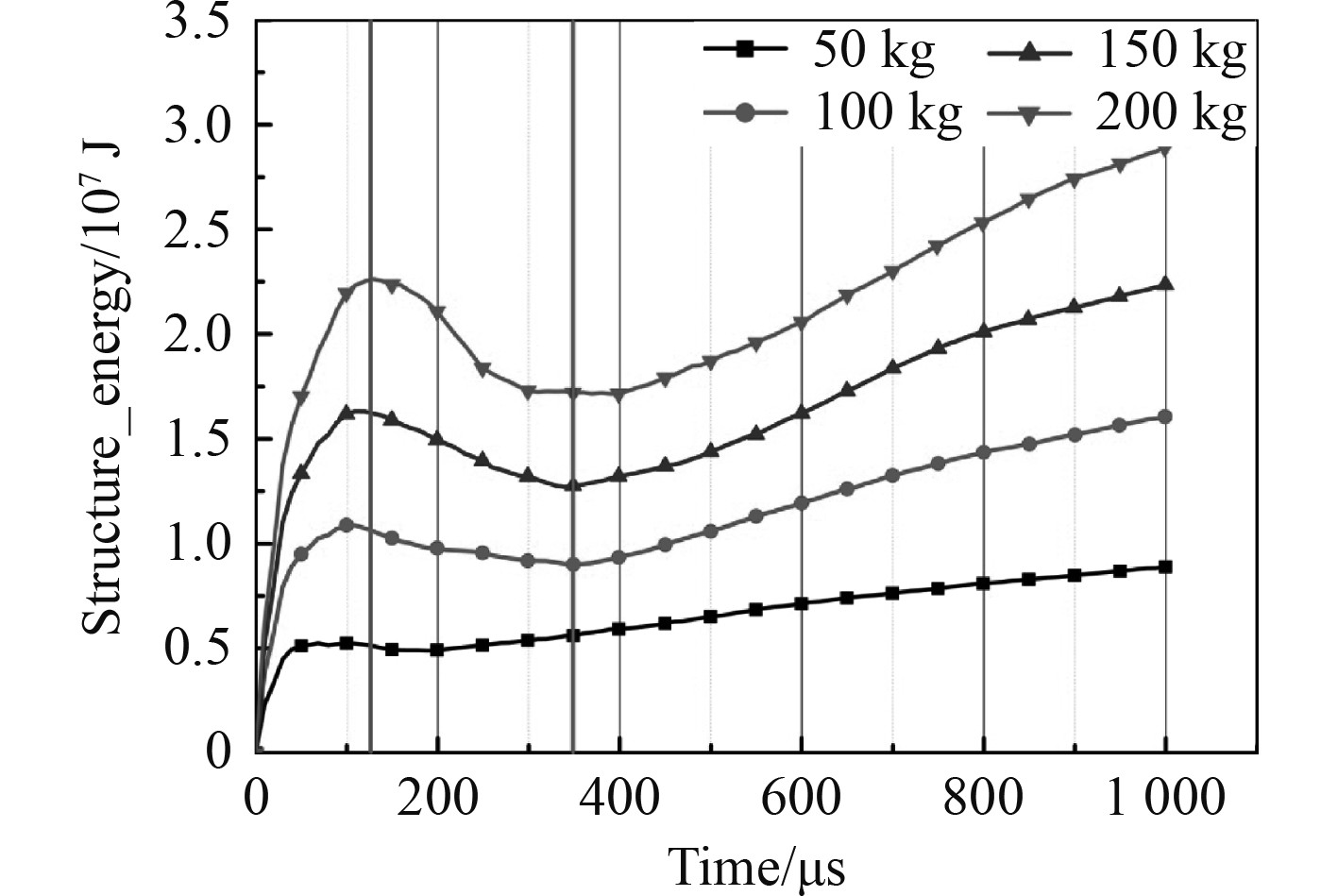
由图14可知，药包质量越大船底结构所获得的能量越大，不同时间内结构吸收的能量是不同的，在0～125 μs间，船底结构获得的能量不断增加，但当超过125 μs后船底分段结构又释放出了一部分能量，然后能量逐步增加。主要原因是当爆炸冲击波传播到船底分段结构时，结构开始获得动能和变形能。在125 μs时达到峰值，随后由于边界条件的影响，能量慢慢耗散，且耗散量大于变性吸收的能量，因此结构的总能量出现下降。随着速度的进一步减小，耗散的能量减少，变形吸收的能量增加，在350 μs时两者几乎相等，随后变形吸收的能量大于耗散的能量，结构的总能量开始缓慢增加。任一时刻结构的能量和炸药的质量呈完全线性关系，具体如图15所示。

3 结　语

本文研究得出结论：

1）初始阶段船底分段结构能量为0，主要是炸药储的化学能量。随着爆炸的进行，炸药的能量一部分传递给船底分段结构，一部分通过热量或其他形式耗散掉了。炸药的能量与炸药的质量成正比，随着时间的增加4种工况下炸药耗散的能量基本相同，因此作用到船底分段结构的能量与炸药量呈正比关系。

2）在被爆结构相同，炸药形状大致一致时，耗散到空气中的能量与炸药的质量呈严格线性关系；船体底部分段各单元受到的最大冲击波压力与药包质量呈非线性关系。