2. 中国船舶科学研究中心 上海分部,上海 200011
2. Shanghai Branch, China Ship Scientific Research Center, Shanghai 200011, China
船型性能的评估是船型设计的重要基础,目前,主要通过经验公式、CFD计算以及模型试验等方法对船舶快速性开展评估,对船型性能进行预报需要经历多个流程,消耗大量的计算资源和时间。随着绿色船型的不断发展,国际海事组织对船舶能效的要求日益提高,水动力节能、主辅机节能、创新节能等节能减排技术的实船应用逐渐成为常态,适应多种节能技术的船型设计和性能快速评估方法也将作为支撑绿色船型研发的重要技术手段。
船型性能的快速评估通常以理论公式、经验公式等显示模型为基础,结合系列化试验建立线性、多项式等线性化层度较高的数学模型,提高船型性能的评估速度[1]。早在20世纪中期,各国学者以扩展的泰勒(Taylor)系列、60系列、BSRA系列、SSPA系列和长江船系列等系列化船型为对象,通过水池试验发展了图谱及回归公式,获得了广泛的工程应用[2]。在船型性能的精确数值预报中,计算流体力学理论、数值仿真技术结合的CFD方法占据着主导地位。
随着数据科学的发展,神经网络、支持向量机、决策树等非线性程度较高的模型在曲面和超曲面拟合方面获得了广泛应用[3],多输入、多输出的黑箱模型在复杂映射关系的辨识中发挥了重要作用,为船型性能评估提供了新的技术手段。数据挖掘是从海量、有噪声的、模糊的数据中发现隐含在其中有价值的信息和知识的过程。21世纪初,Haddara[4]、Hess[5]、Chiu[6]、Besnard[7]等应用神经网络、支持向量机、加权回归和多目标优化等算法,开展了基础模型的船舶性能预报与优化。近年来,张恒等[8]基于径向基神经网络利用回归分析法,开展了船型主尺度参数对阻力性能的敏感度研究;肖振业等[9]将支持向量机用于船舶阻力的性能预报。
本文在船体型线特征参数表达与提取、船型快速性评估方法的基础上,融合数据挖掘技术,研究船型特征参数与快速性能之间的映射关系和相关性。为满足数据挖掘对样本数量要求,本文主要以超大型油船的粘势耦和计算结果为性能指标,将超大型油船历史设计船型作为样本集,研究船型参数与CFD计算获得的剩余阻力系数Cr、伴流分数w、兴波阻力系数CWTW、粘压阻力系数Cpv之间的映射关系及相关性,分析各船型参数对各性能参数的影响。
1 超大型油船型特征参数及样本分布本文以超大型油船为研究目标,收集超大型油船历史设计船型作为样本集,通过CFD方法计算获得对应的剩余阻力系数Cr、伴流分数w、兴波阻力系数CWTW、粘压阻力系数Cpv,形成分析所需要的数据集。船型参数化表达是以船体几何测量量、微分量、积分量等数值描述整个船型几何特点的方法,本文采用的船体型线特征参数化方法是参考现有的经典船舶参数、船体几何全参数表达等方法整合得到的船体型线多层次特征参数表达方法。该方法将船型参数分为船体全局参数、局部和细部参数,本文共计使用了133个参数。船型特征参数分类方法如表1所示。
|
|
表 1 船型特征参数分类 Tab.1 Classification of ship type characteristic parameters |
超大型油船数据集样本部分参数分布如表2所示。
|
|
表 2 超大型油船数据集样本主尺度分布 Tab.2 Sample principal scale distribution of VLCC data set |
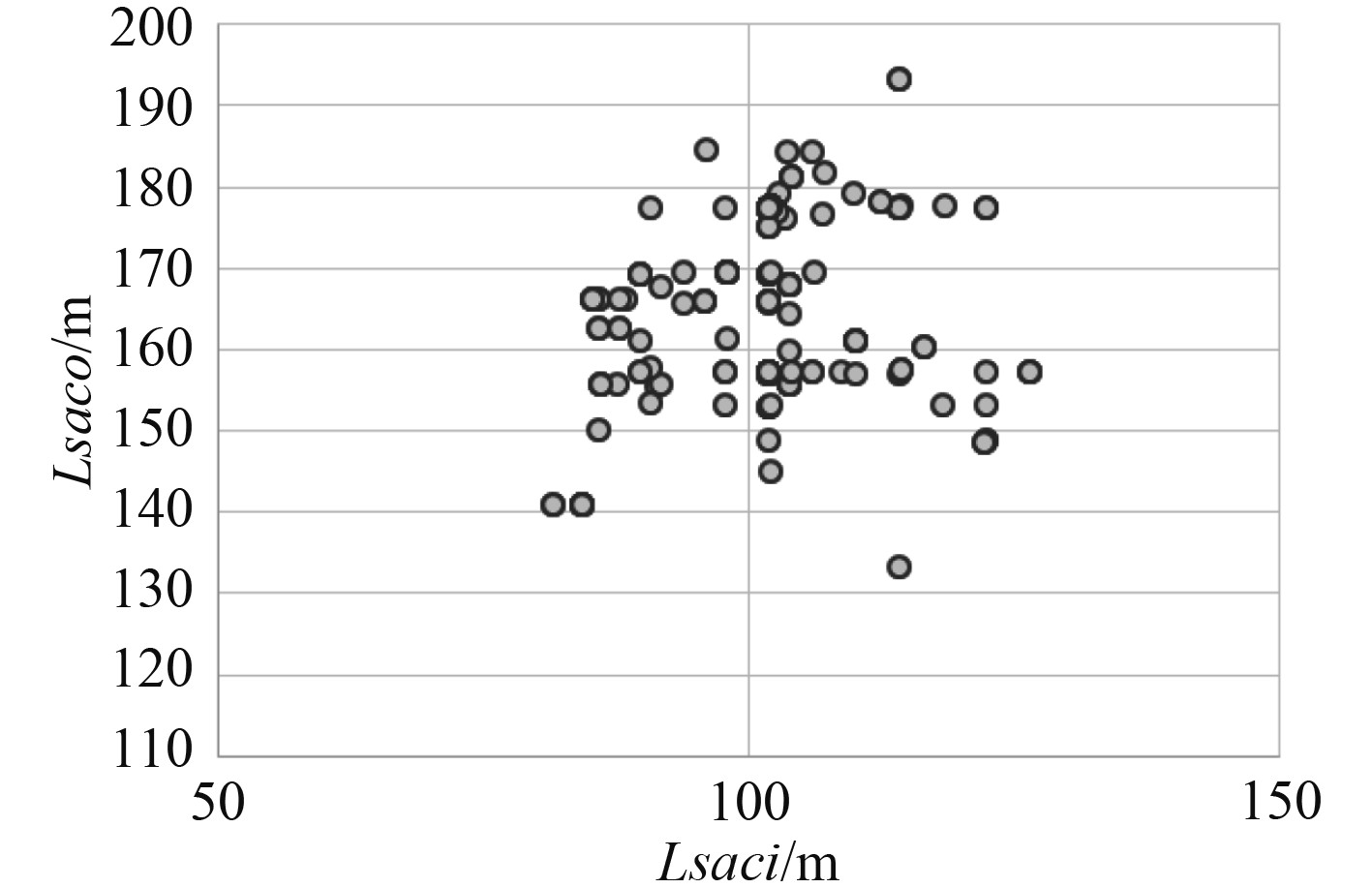
由于该样本中的船型为设计过程中同一母型船变形得到,因此船型主尺度相近,局部线型相差较大。图1为样本集垂线间长Lpp和方形系数分布Cb的分布情况,可见该样本集合船型主参数比较接近。图2为样本集首分段长度lsaci和方形系数分布,可见该样本集合局部线型差异比较大。因此,该样本集适用于对局部参数和细部参数的分析。

|
图 1 样本集垂线间长Lpp和方形系数分布Cb Fig. 1 Distribution of length between vertical lines Lpp and square coefficient Cb of data set |
|
图 2 样本集首分段长度lsaci和尾分段长度lsaco分布 Fig. 2 Distribution of bow section length lsaci and stern section length lsaco of data set |
本文使用的数据集以历史船型为主,船型特征参数分布不均匀,可能存在少数优化过程中产生的中间船型,这些船型与其余样本差距较大。因此,需要在开展分析之前对数据进行处理,去除样本中的数据孤点或者异常点。采用人工处理的方法难度较大、无法遍历全参数。中心点距离判据是一种应用广泛的数据簇划分方法,它是k临近算法、k均值算法等以距离作为判定条件的算法的核心。其中心思想是通过设定、求解数据集的中心(也称为质心),计算各个样本到中心的距离,对样本进行分簇。本文通过计算各个样本到中心点的距离,去除距离中心点较远的样本点,清除数据孤点。
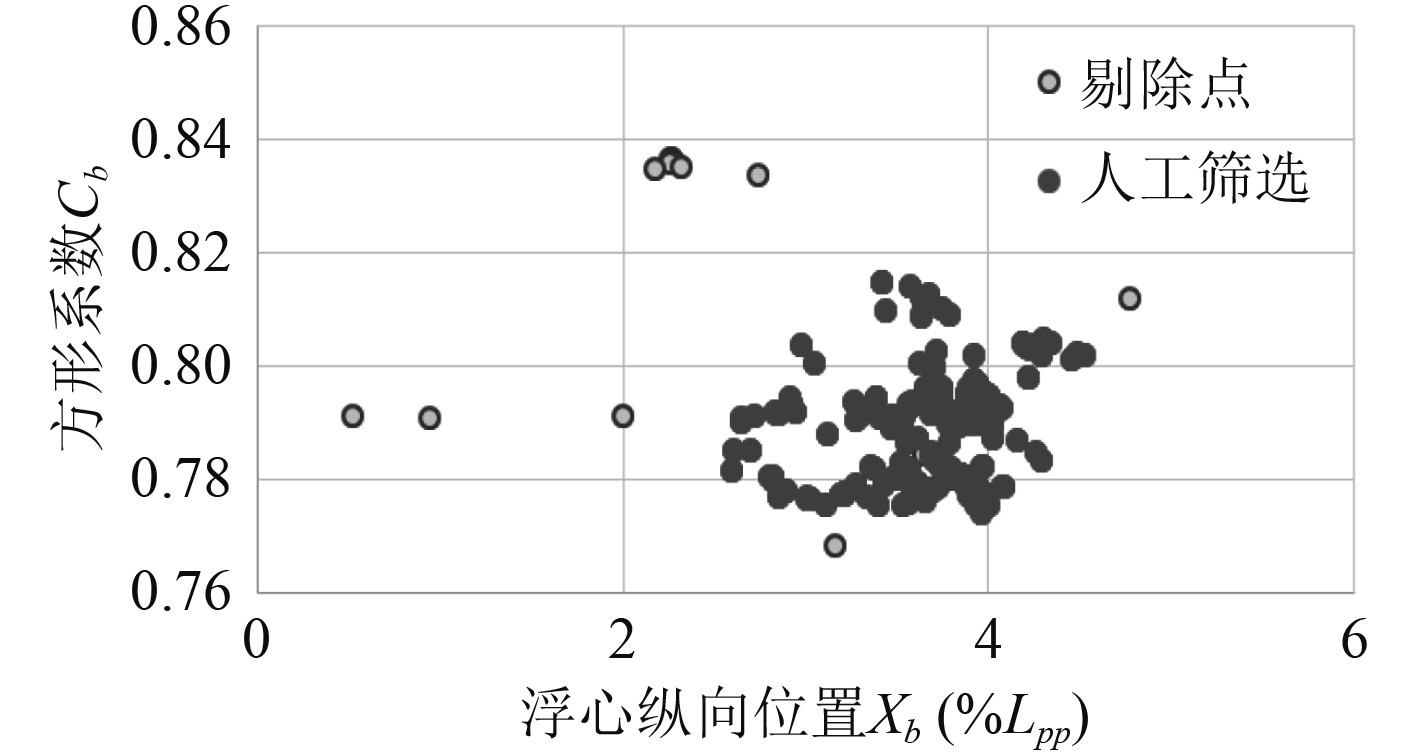
采用人工筛选和基于中心点距离的方法对数据集进行处理,其中基于中心点距离的方法分别选择方形系数Cb&浮心位置Xb、全参数2种组合作为输入。筛选结果如图6~图9所示。
|
图 3 经人工筛选后的参数分布 Fig. 3 Parameter distribution after manual screening |
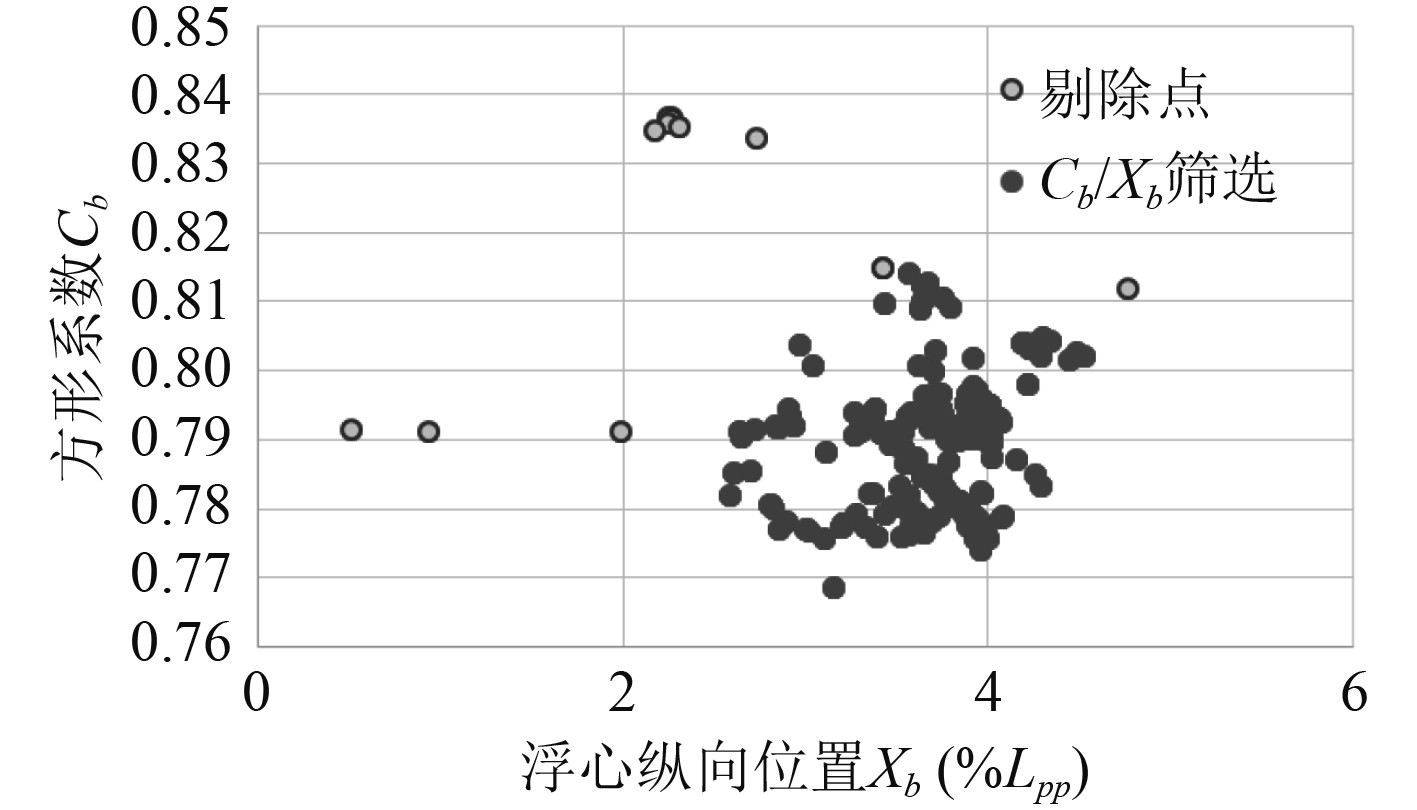
|
图 5 经Cb&Xb筛选后的参数分布 Fig. 5 Parameter distribution after Cb&Xb screening |

|
图 6 Mean-E%随惩罚系数C影响 Fig. 6 Variation of Mean-E% with penalty coefficient C |

|
图 8 Mean-E%随惩罚阈值tol影响 Fig. 8 Variation of Mean-E% with penalty threshold tol |
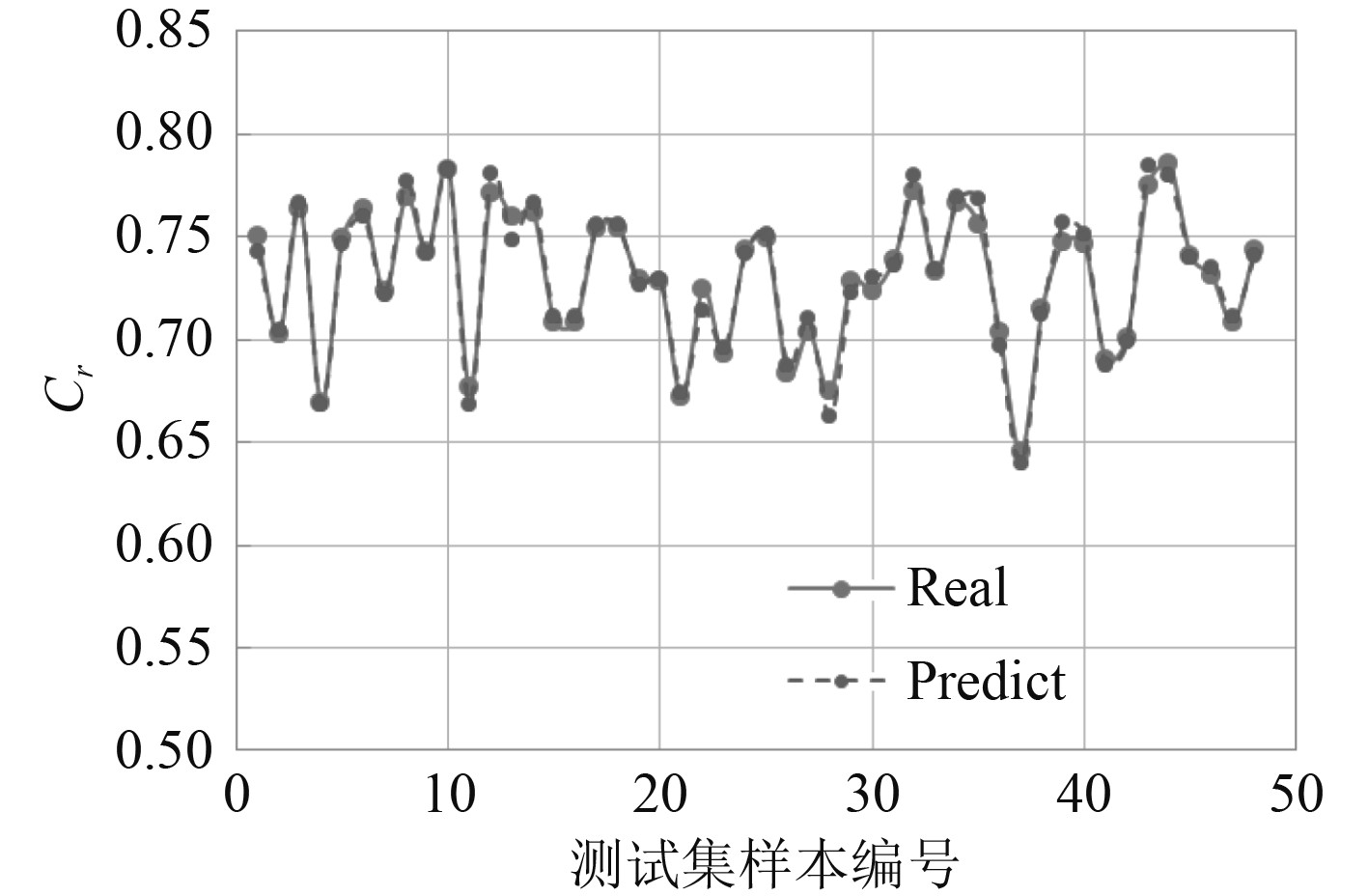
|
图 9 剩余阻力系数Cr模型预报结果 Fig. 9 Prediction results of residual resistance coefficient Cr model |
通过对比可发现,以人工筛选(人为经验性选择)为参考,经Cb&Xb筛选后的数据集与人工筛选结果最为接近,经全参数筛选后数据集部分孤立数据点未被剔除。因此,本文采用Cb&Xb筛选方法对数据进行处理。
2 支持向量机支持向量机(Support Vector Machine,SVM)这种分类器的特点是其能够同时最小化经验误差与最大化几何边缘区。针对线性可分情况,采用线性回归函数进行拟合:
| $ f\left(x\right)=\omega x+b,$ | (1) |
对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能。
| $ f\left(x\right)={\sum }_{i=1}^{n}{\omega }_{i}K(x,x{'})+b 。$ | (2) |
本文采用SVM方法作为模型,将90%的样本作为训练集,10%的样本作为测试集。通过对比测试集预报结果与真实值得相对误差,计算该误差的均值Mean-E%,评估模型的预报效果。回归前先开展数据归一化,归一化方法如下:
| $ {P}_{i,j}^{{'}}=\frac{{P}_{i,j}^{{'}}-\underset{j\in [0,n]}{min}\left({P}_{i,j}^{{'}}\right)}{\underset{j\in [0,n]}{max}\left({P}_{i,j}^{{'}}\right)-\underset{j\in [0,n]}{min}\left({P}_{i,j}^{{'}}\right)}。$ | (3) |
其中:i为船型参数序号;n为样本船型总数;P为船型参数;j为样本编号。本文以使用RBF函数作为SVM的核函数,对SVM的惩罚系数C、归一化之后的惩罚半径epsilon、惩罚阈值tol对模型预报精度的影响进行研究。通过对比测试集预报结果与真实值得相对误差,计算该误差的均值Mean-E%,评估模型的预报效果。Mean-E%的计算公式如下:
| $ Mean - E\% = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right|} \times 100\% 。$ | (4) |
其中:N为测试样本数量;y为样本真实值;
SVM的惩罚系数C取为3000~3500左右可兼顾预报精度与鲁棒性,惩罚半径epsilon小于0.01时预报精度较高且相对稳定,惩罚阈值tol小于0.0001时预报精度较高且相对稳定。剩余阻力系数Cr、伴流分数w、兴波阻力系数CWTW、粘压阻力系数Cpv的SVM模型在测试集上的预报模型如图4~图7所示。

|
图 4 经全参数筛选后的参数分布 Fig. 4 Parameter distribution after full parameter screening |

|
图 7 Mean-E%随惩罚半径epsilon影响 Fig. 7 Variation of Mean-E% with penalty radius epsilon |
|
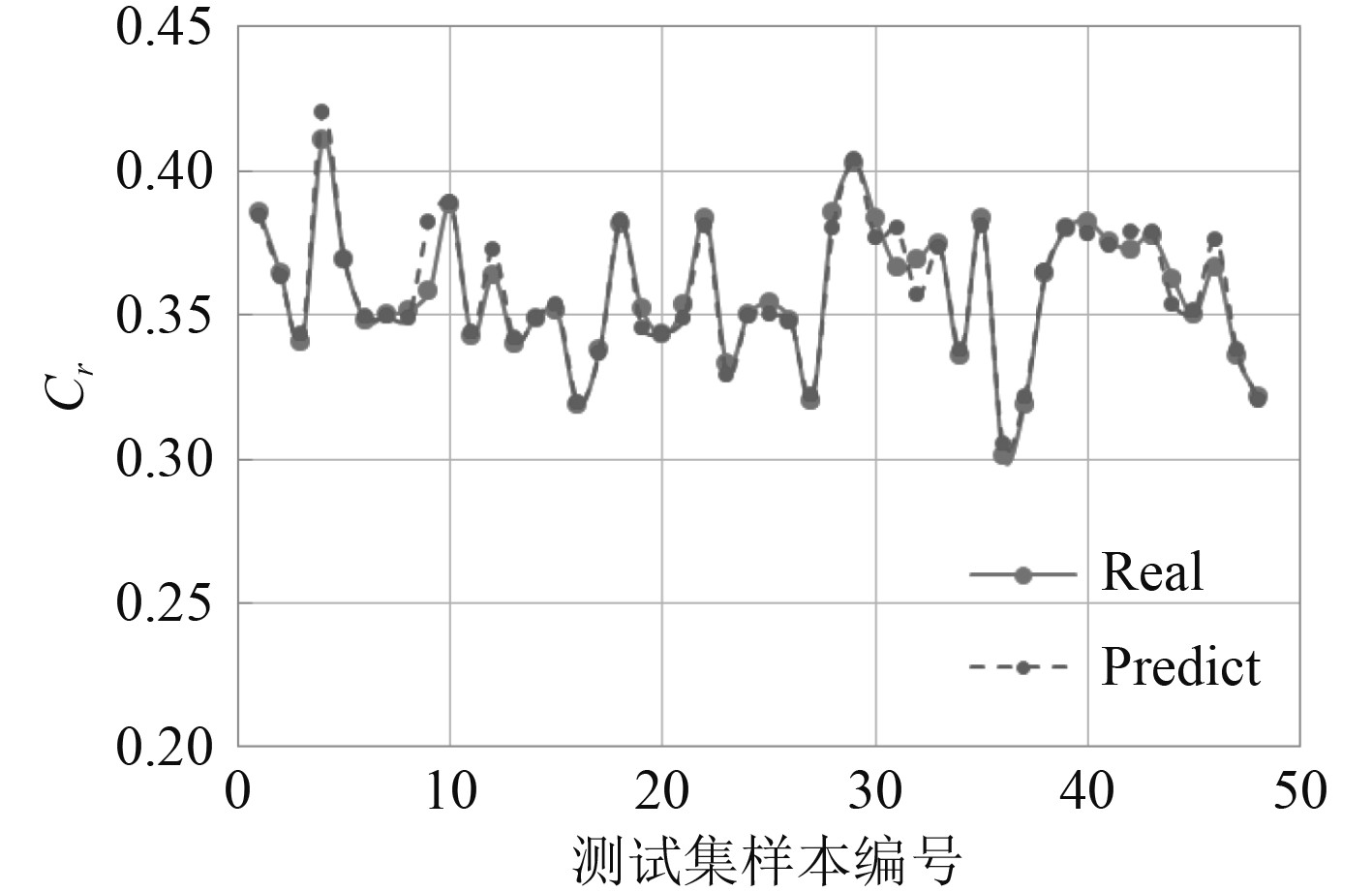
图 10 伴流分数w模型预报结果 Fig. 10 Prediction results of wake fraction w model |

|
图 11 兴波阻力系数CWTW模型预报结果 Fig. 11 Prediction results of wave making resistance coefficient CWTW model |

|
图 12 粘压阻力系数Cpv模型预报结果 Fig. 12 Prediction results of viscous pressure resistance coefficient Cpv model |
计算剩余阻力系数Cr、伴流分数w、兴波阻力系数CWTW、粘压阻力系数Cpv的SVM模型样本空间以及预报误差的均值和标准差如表3所示。
|
|
表 3 模型预测误差统计 Tab.3 Model prediction error statistics |
从结果上看,SVM模型对兴波阻力系数CWTW和伴流分数w的预报结果相对误差较高,主要原因是CWTW和w的均值相对较小,而且CWTW和w的变化范围相比于Cr与Cpv更大。因此,模型对CWTW和w的预报结果相对误差较高,而Cr实际预报结果的绝对误差的均值为0.0045,w实际预报结果的绝对误差的均值为0.0037,CWTW实际预报结果的绝对误差的均值为0.000086,Cpv实际预报结果的绝对误差的均值为−0.00014。
3 参数敏感性分析敏感性分析指在一个数学模型中根据输入变量的变化观测输出变量的变化,确定灵敏度大小的方法。本文选用的敏感性分析方法为:LH-OAT方法和Sobol方法。
OAT方法是筛选法中最简单的一种方法,这种方法的特点是每次只能分析一个因素对输出的影响[10]。OAT敏感性分析法在Monte Carlo抽样方法的基础上进行重复试验,每次对其中一个参数进行微小的扰动,保持其他参数不变,代入敏感性公式,即可得到每个参数的敏感度,具有较高的精确性。但Monte Carlo抽样法在参数取值范围内随机抽样,会产生大量的样本,使OAT敏感性分析方法的运算量变大。LH-OAT全局敏感性分析方法则是在OAT敏感性分析法的基础上采用Latin-Hypercube抽样代替Monte Carlo抽样,减少了采样频次,能提高敏感性分析的效率。
Sobol方法是Sobieski在1990年提出的一种基于Monte Carlo积分灵敏度分析方法,是一种基于方差分解(Analysis of Variance,ANOVA)的方法[11]。
本文应用LH-OAT方法和Sobol方法对剩余阻力系数Cr、伴流分数w、兴波阻力系数CWTW、粘压阻力系数Cpv进行敏感性分析,将不同模型计算获得的敏感性指标绝对值最高的前10个参数进行对比分析,结果如表4所示。
|
|
表 4 敏感性指标对比 Tab.4 Comparison of sensitivity indexes |
其中l2d为2站下反曲点至尾轴中心距离;Cwi为进流段水线面系数;Cwo为去流段水线面系数;Cpa为尾部棱形系数;b2d为2站下反曲点半宽;Cba为尾部方形系数;b1_5 m 为1.5站中反曲点半宽;lpp_B为长宽比;b1u为1站上反曲点半宽;tetw1为1站纵向夹角;Xb为浮心纵向位置;Cpv为垂向棱形系数;zclear为尾轮廓反曲点高度;B4为4站半宽;D为型深;l1_5s 为1.5站中反曲点到尾轴中心线距离;l1t为1站中反曲点到切线距离;b1m 为1站中反曲点半宽;x1_5为1.5站UV度特征值;b1_5d 为1.5站下反曲点半宽;b2m为2站中反曲点半宽;Cb为方形系数;l1d为1站下反曲点至尾轴中心距离;xfdb为首轮廓起点位置;B16为16站半宽;h1_5m为1.5站中反曲点高度;l1s为1站中反曲点到尾轴中心线距离;h1m 为1站中反曲点高度;l2s为2站中反曲点到尾轴中心线距离;l1_5d为1.5站下反曲点至尾轴中心距离;c2为2站处横剖面系数;h2d为2站下反曲点高度; lsaci为首分段长度;Lwlm为中体长度;B16为16站半宽;lsaco为尾分段长度;x19_5为19.5站UV度特征值;B17为17站半宽;afc为直首侧投影面积;lcfobi为首分段包络面形心纵向位置;Lcf为漂心纵向位置。
4 结 语本文以超大型油船历史数据为基础,采用SVM方法建立船体性能预报模型,联合敏感性分析方法,研究超大型油船型特征参数对快速性能影响研究,形成的结论如下:
1)支持向量机(SVM)方法对兴波阻力系数CWTW的预报结果相对误差均值0.959%,标准差为10.10%,对伴流分数w的预报结果相对误差均值0.151%,标准差为1.556%,对剩余阻力系数Cr的预报结果相对误差均值0.027%,标准差为0.766%,对粘压阻力系数Cpv的预报结果相对误差均值0.003%,标准差为1.050%;
2)依据本文的分析结果,Cpa尾部棱形系数、Cba尾部方形系数、zclear尾轮廓反曲点高度、Cpv为垂向棱形系数、1~2站局部线型特征对剩余阻力系数Cr和伴流分数w的影响较大;
3)依据本文的分析结果,1~2站反曲点半宽、高度、UV度特征值等局部线型特征对粘压阻力系数Cpv的影响较大;
4)依据本文的分析结果,1~2站局部线型特征、16~17站局部线型特征、首尾分段长度、包络面形心纵向位置对兴波阻力系数CWTW的影响结果。
| [1] |
曾帅. 典型海况下的船舶阻力预报研究[D]. 大连: 大连海事大学, 2020.
|
| [2] |
黄超. 肥大型船舶阻力快速预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [3] |
何清, 李宁, 罗文娟, 等. 大数据下的机器学习算法综述[J]. 模式识别与人工智能, 2014, 27(4): 327-336. DOI:10.3969/j.issn.1003-6059.2014.04.007 |
| [4] |
HADDARA M. R, WANG Y. Parametric identification of manoeuvering models for ships[J]. International Shipbuilding Progress, 1999, 46(445): 5-27. |
| [5] |
HESS D. FALLER W. Simulation of ship maneuvers using recursive neural networks[C]. 23th Symposium on Naval Hydrodynamics, Washington D. C. (USA): National Academies Press, 2000: 223–242.
|
| [6] |
CHUI F C, CHANG T L, et al. A recursive neural networks model for ship maneuverability prediction[C]//Proceeding Oceans MTS/IEEE Techno-Ocean, Kobe(Japan): EEEE, 2004: 1211–1218.
|
| [7] |
BESNARD E, SCHMITZ A, HEFAZI H, SHINDE R. Constructive neural networks and their application to ship multi-disciplinary design optimization[J]. Journal of Ship Research, 2007.
|
| [8] |
张恒, 詹成胜, 刘祖源, 等. 基于船舶阻力性能的船型主尺度参数敏感度分析[J]. 船舶工程, 2015(6): 11-14. DOI:10.13788/j.cnki.cbgc.2015.06.011 |
| [9] |
肖振业, 冯佰威, 刘祖源, 等. 基于支撑向量机的船舶阻力近似模型[J]. 计算机辅助工程, 2015, 24(4): 20-23. |
| [10] |
夏露, 杨梅花, 李朗, 等. 基于全局灵敏度分析方法的气动设计研究[J]. 西北工业大学学报, 2018, 36(1): 49-56. DOI:10.3969/j.issn.1000-2758.2018.01.008 |
| [11] |
孙毅. 基于LH-OAT的推理公式法参数敏感性分析[J]. 水利发电, 2017, 43(9): 23-25. |
 2023, Vol. 45
2023, Vol. 45
