0 引　言

在舰船航行过程中，舰船路径规划是否合理直接关系到舰船航行任务能否得以有效完成。因此，舰船路径规划方法设计是当前的重要研究课题^[1]。

国内外诸多学者对舰船路径规划优化方法进行了大量研究，张兰勇等^[2]针对传统RRT*舰船路径规划方法进行改进，在舰船路径规划过程中，把偏置函数加入其中，使用Dubins曲线对采样点实施平滑性连接；杨兵等^[3]利用激光雷达图像对栅格化舰船航行环境信息执行合理生成操作，并通过维诺场算法将危险势场添加给各栅格，构建舰船航行边界以及与舰船航行边界相关的危险度函数，改进A*算法中的评价函数完成舰船路径规划与优化工作。对于复杂海洋航行环境中，以上的舰船路径规划与优化效果不太理想^[4]。

粒子群算法具有路径寻优速度快、精度高等优势，为了更为理想的舰船路径规划与优化效果，设计了改进粒子群算法的舰船路径优化方法，并对性能进行测试与分析。

1 舰船路径优化 1.1 舰船航行海面路线图构建

将概率图法应用于舰船路径优化，对舰船航行路线图执行有效构建操作。在较为复杂的海面空间中，确定了舰船的出发点以及目的点后，可在剩余区域挑选1个点，利用碰撞检测的方式对该点执行合理分析操作。若该点隶属自由空间，便将其当作舰船航行路径节点，放入路线图存储；若该点隶属威胁空间，则将其清除。把确定的新节点与路线图中已经存在的路径节点连接起来，并不断循环执行此操作，便可完成相应的舰船航行路线图构建操作，具体过程可归结为：

1）在舰船航行海洋区域，对舰船航行路径网络实施合理构建，并将构建出的路径网络标记为U，满足

$ {U=}（N,E） 。$

(1)

式中：N为随机性质路径节点所组成的集合；E为任意2个航行路径节点之间可能会存在的航行路径。

2）对路径节点实施随机设定，并将设定完成的舰船航行路径节点放入 $ N $ 内。设定的路径点必须在自由空间内，并且节点不会与障碍物出现碰撞。

3）用b标记新产生的舰船航行路径节点，在 $ N $ 中挑选出一些与之相邻的节点p，并利用局部路径规划装置对局部路径进行合理规划。

4）经上述操作后，可将舰船航行所产生路径的边界标记为(b,p)，将(b,p)放入 $ E $ 实施合理存储，与此同时清除掉不具有可行性的舰船航行路径。

1.2 舰船航行路径优化模型构建

按舰船在航行性能方面的评价指标，通过执行有效的规划操作，得到舰船航行路线图中的最优航行路径，即获得一条从舰船出发点U_s到舰船航行目的地U_G，并满足一系列约束的舰船航行路径，该路径可描述为：

$ \varGamma = \left\{ {{U_S},{U_1},{U_2},\cdots ,{U_{n - 1}},{U_n},{U_G}} \right\} 。$

(2)

式中： $\varGamma$ 为舰船航行路径； $ {U_i} $ 为路径节点， $ i $ 为1~n的整数； $ n $ 为路径节点数量。

在复杂舰船航行海面环境状况下，构建出的舰船航行路径优化模型为：

$ \mathop {\min }\limits_\gamma G = YSL\rho {v^2} \div 2Q。$

(3)

式中： $ G $ 为舰船在航行性能方面的评价指标； $ Y $ 、 $ \gamma $ 分别为水动力性系数以及根据舰船航行状况设置的约束条件； $ \rho $ 为海水密度； $ v $ 为舰船在海域航行的速度值； $ S $ 和 $ L $ 分别为舰船的横截面面积以及舰船航行时路径的长度；Q为舰船的机械效率。具体的约束条件有：

$ \left\{ \begin{gathered} \forall \left( {x,y} \right) \notin {H_f},f\left( {x,y} \right) = 0 ，\\ {L_{\max }} > L_g^{} + {\delta _g}，\\ \varphi \geqslant {\phi _i}，\\ {S_k} = \sum\limits_{i = 1}^{m - 2} {\frac{{{e^\partial }\left( {R - {r_i}} \right)}}{L}} \leqslant {S_{\max }}。\\ \end{gathered} \right. $

(4)

式中：H_f为经膨胀化处理操作后获得的舰船不能航行区域集合；f(x,y)=0为规划出的用于表示舰船最优航行路径的曲线，(x,y)为路径上任意一个点所拥有的坐标； $ \forall \left( {x,y} \right) $ 为船舶实际航行路线；L_g为规划出最优舰船航行路径的长度；L_max为舰船拥有能源能够完成航程的最高限值； $ {\delta _g} $ 为舰船航行时实际以及规划出路径之间存在的偏差； $ {\phi _i} $ 为舰船航行转弯角； $ \varphi $ 为转弯角最高限值；S_k、 $ \partial $ 分别为第 $ k $ 条舰船航行规划路径所累计的转弯角度以及离散性系数； $ R $ 、r_i分别为舰船航行路径所拥有的转弯角度最高值、所规划舰船航行路径上编号为 $ i $ 的转向点所拥有的转弯角度用标记；S_max为舰船航行路径能够达到的平滑度最高值； $ m $ 为舰船航行路径点的总体数量； $ e $ 为一个常指数。

1.3 粒子群优化算法舰船航行路径优化模型求解 1.3.1 改进粒子群算法

粒子群优化算法利用各粒子间的信息共享以及协作能力搜寻最优解^[5]。鉴于其强大的寻优性能，将其应用于舰船路径优化，使用改进粒子群算法对构建的舰船航行路径优化模型执行合理求解操作。改进粒子群算法、基本粒子群算法，在舰船航行路径优化模型求解工作中的不同之处主要有：

1）执行随机性质权重设置操作。在利用基本粒子群算法对舰船航行路径优化模型求解时，通常在整个求解过程中，只是采用一个不变的常数值当作惯性权重。如果该常数的值很小，那么在模型求解前期对全局搜索会产生非常不利的影响；如果该常数的值非常大，那么在模型求解后期，又会对局部搜索操作产生非常不利的影响，这无疑会在很大程度上降低模型的收敛速度。为此，通过设置具有随机特性的权重，避免上述问题发生。设置的随机性质权重可描述为：

$ w = {w_{\min }} + \left( { - {w_{\min }} + {w_{\max }}} \right) \cdot {\rm{rand}}() + z \cdot {\rm{rand}}n() 。$

(5)

式中： $ w $ 、w_max与w_min分别为随机性质惯性权重以及其最大、最小值；rand()为在0～1中间以相对均匀特征分布的各随机数；randn()为呈现正态分布特征的随机值； $ z $ 为满足正态分布特征的随机性质扰动项所拥有的标准性偏差。

2）为扰动性粒子增添有效的更新机制。在利用基本粒子群算法解决舰船最优路径规划问题时，各粒子除按经验搜寻较优越的速度以及位置以外，互相之间只是能够对种群中拥有的最优粒子所携带的信息进行合理共享。如此显然会降低获得最优解的概率。不仅如此，若各粒子本身历史性最优方位与粒子种群所拥有最优方位所产生的方向性夹角过于小，那么还会使算法陷入到局部最优的困境。为此，在基本粒子群算法基础之上，增添扰动粒子，并为扰动性粒子增添有效的更新机制，用来增强粒子寻优能力。如此操作后，粒子的速度以及位置更新过程可描述为：

$ \left\{ \begin{split} {v_{i,j}}\left( {t + 1} \right) =& w{v_{i,j}}\left( t \right) + {c_1}{r_1}\left[ {{q_{i,j}}\left( t \right) - {x_{i,j}}\left( t \right)} \right] + \\ & {c_2}{r_2}\left[ {{q_{g,j}}\left( t \right) - {x_{i,j}}\left( t \right)} \right] + {c_3}{r_3}\left[ {{q_{d,j}}\left( t \right) - {x_{i,j}}\left( t \right)} \right] ，\\ {x_{i,j}}\left( {t + 1} \right) =& {x_{i,j}}\left( t \right) + {v_{i,j}}\left( {t + 1} \right) 。\end{split} \right. $

(6)

式中：c₁为自我认知性因子；c₂为社会认知性因子；c₃为扰动性因子；r₁、r₂为在0～1范围内呈现均匀分布状态的随机数；r₃为在−1～1范围内呈现均匀分布状态的随机数；v_i,j(t)、v_i,j(t+1)分别为粒子更新前后的运动速度；x_i,j(t)、x_i,j(t+1)分别为粒子更新前后的位置信息；q_i,j(t)为粒子的个体极值点位置；q_g,j(t)为粒子群体的全局性极值点位置；q_d,j(t)为扰动粒子的个体极值点位置； $ {c_3} \cdot {r_3} \cdot \left[ {{q_{d,j}}\left( t \right) - {x_{i,j}}\left( t \right)} \right] $ 为增加的粒子速度扰动项。

1.3.2 改进粒子群算法舰船航行路径优化模型求解

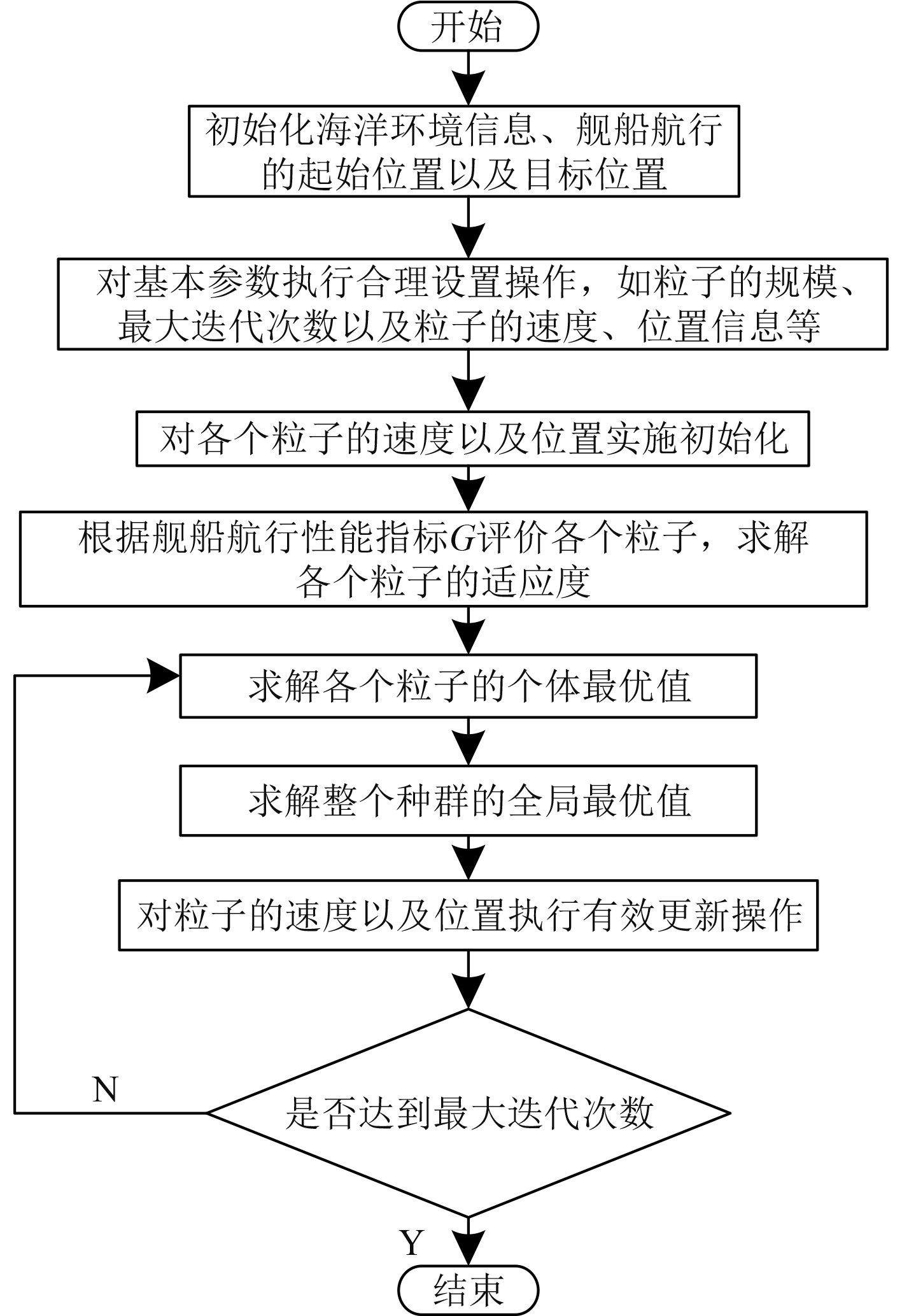
针对舰船在复杂海洋环境下的最优航行路径求解问题，本文应用改进粒子群算法对构建的舰船航行路径优化模型实施合理求解，求解流程如图1所示。利用改进粒子群算法求解舰船航行路径优化模型的最终目的是在构建的舰船航行线路图中找到一条满足最优标准的合理解向量。在改进粒子群算法路径寻优过程中，不同粒子的位置可理解成舰船航行线路图中的任意航行路径，在经过各参数初始化、粒子评价以及适应度求解等操作后，经过无数次的迭代操作，便可收获具有全局性质最优舰船航行性能指标的粒子所表示的舰船航行路径。

1.3.3 舰船最优路径平滑优化

通过改进粒子群算法求得的舰船航行最优路径，尽管在路径平滑度以及耗能方面，比其他舰船航行路线具有非常显著的优势，但由于其通常还是由若干路径点构成的折线，因而舰船在完成实际航行任务时，转弯次数可能仍然会较多，并且当所获舰船航行最优路径的某些航段具有非常短的距离时，可能在转向点位置处，还会出现转弯角太大的情况，这显然会对舰船的安全航行造成非常不利的影响。为此，在利用改进粒子群算法获取到舰船航行初始最优路径后，将路径平滑处理操作引入其中，显著降低舰船航行时的转弯次数，使获得的舰船最优航行路径更具实用性。

对舰船最优航行路径实施平滑处理的实质是最大限度地进行截弯取直，使用直线对各路径点实施有效连接，降低舰船在转弯时的角度，与此同时，让舰船在各个航段航行时的距离保持合理的长度。对于经改进粒子群算法求得的舰船航行最优路径序列而言，平滑优化的步骤可简单归结为：按所获舰船最优航行路径中所显示的序列顺序，以首个路径点为起点，和最末尾的路径点连接。如果获得的线段没有穿过障碍物，那么可将该段路径放入路径序列内，当作舰船全局航行路径中的子路径段，反之将其与前方路径点连接。如此操作，经过无数次循环，一直到倒数第二的路径点方可停止。这样便可获得更为理想的舰船航行最优路径。

2 实验分析

以某艘运输船为实验对象，应用Matlab软件模拟本文方法对其实施路径优化过程。该船长在450 m左右，宽在70 m左右，单次货物运载能力可达13200 TEU，其承担的主要职责是向东南亚某国客户运输货物以及装备，航行所经海域环境较为复杂。实验中粒子群优化算法各项参数的设定情况如表1所示。

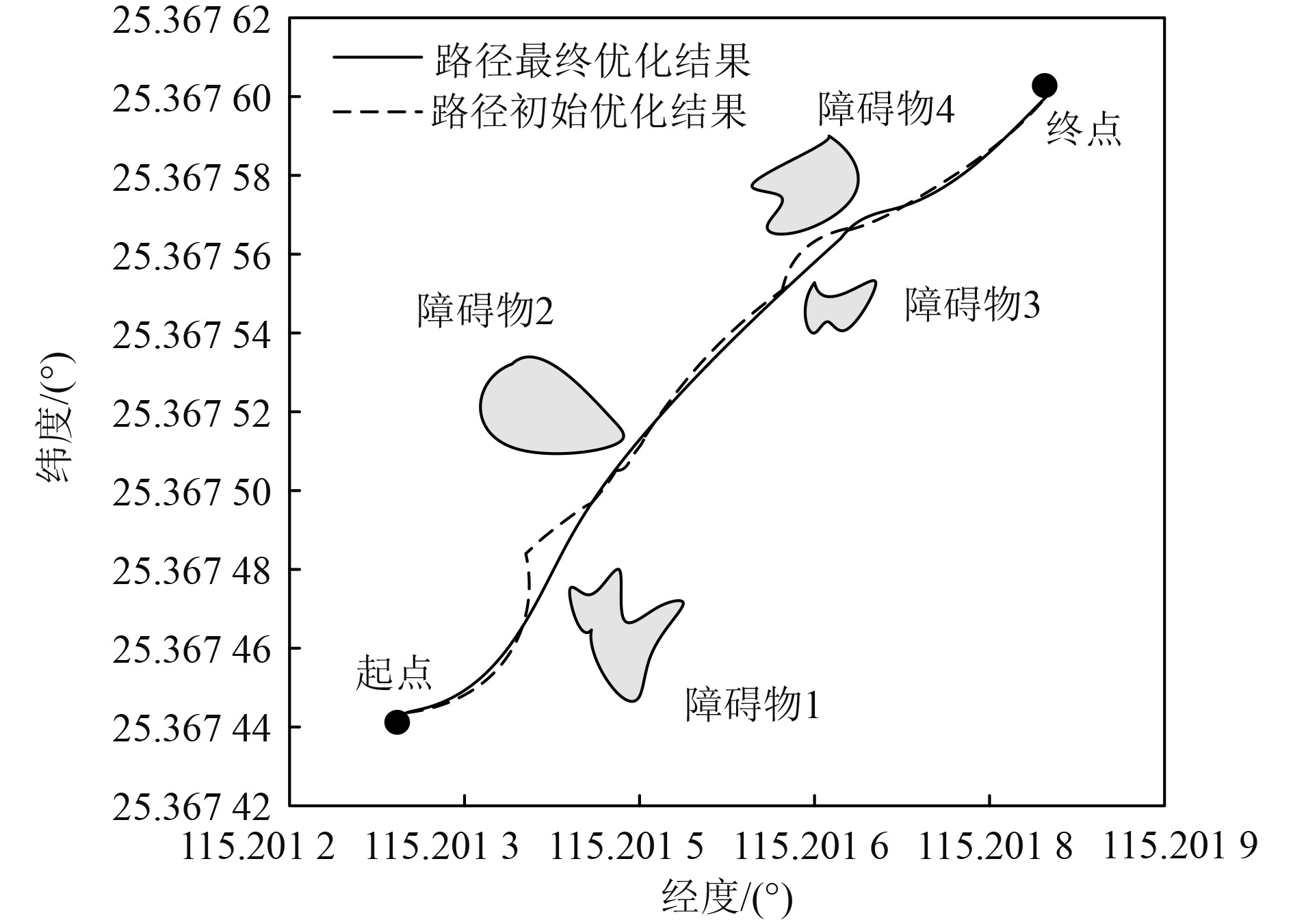
应用本文优化仿真方法对舰船航行路径实施合理优化，获得的舰船路径优化结果如图2所示。可知，应用本文方法可以实现舰船路径优化，更好满足实际需要，为舰船续航能力的显著提高提供可靠保障。

为进一步验证本文方法在舰船路径优化方面的有效性，在实验中设置9个舰船航行任务，并分别应用基本粒子群算法、改进粒子群算法，对各个舰船航行任务所对应的舰船路径优化模型实施合理求解，获得的舰船路径优化效果对比如表2所示。可知，应用改进粒子群算法对舰船路径优化模型实施合理求解后，所获舰船最优路径的长度要更短，转弯点数量要更少，并且最大转弯角的角度也更小。表明，本文方法在舰船路径优化中优势显著，可收获效果理想。

3 结　语

本文方法能够有效优化舰船路径，优化后的舰船航行路径长度更短、转弯点数量更少、最大转弯角的角度值也更低。在实际应用中，舰船可更快、更为准确地完成航行任务。