随着海洋运输在国际商品交换中所占比重越来越大,船舶航线优化被提到了重要的地位。该领域研究的问题是在考虑风浪环境条件的情况下,寻找给定航行的最优路径和航速,目标通常考虑最小航行时间、燃油消耗或通行风险[1]。
近年来,多目标航线优化得到了较多关注,它可以同时针对多个目标进行优化,进而产生大量的权衡解,决策者可根据当前的需要确定最终的航行方案。目前,进化算法在解决该问题上取得了广泛应用[2-3],主要包括经典算法SPEA2[4]、NSGA-Ⅱ[5]以及一些改进的算法NMOEA[6]、SPEA2+[7]。然而,由于规划过程中存在庞大的样本量和优化空间,收敛效率慢成为普遍现象。特别是随着迭代步长的增加,搜索样本量的限制还可能导致算法陷入局部最优。
本文针对SPEA2在解决多目标航线优化问题中存在的收敛速度慢和易陷入局部最优的现象进行改进。通过Dijkstra算法搜索的可行解加入到初始种群中作为引导以加快算法寻优的效率;采用更精细化的选择过程保证精英个体可继续参与进化;提出新的交叉和变异策略,有效提升了种群质量。
1 SPEA2算法改进 1.1 SPEA2的基本思想Zitzler[4]提出的强度Pareto进化算法(SPEA2)是一种多目标进化算法,具有良好的搜索性能,它包含一些重要的操作,例如在适应度分配策略中,同时考虑了种群中的显性个体和隐性个体,提高了全局搜索能力;计算最近相邻个体的密度提高搜索精度;采用新的存档截断方法,保证边界解得以保留。
1.2 改进工作的动机大多数优化算法无法找到更高质量的解,主要因为它们工作效率较低。例如,当种群中的大多数解处于非支配阶段时,粗糙的选择方法将剥夺优势精英继续参与进化的机会,导致优化结果停滞或更差。同时,交叉机制作为进化算法中生成新个体和扩展解空间的一种有效方法,还尚未被有效探索。尤其当种群中个体间差异较小时,算法易进入停滞状态,这时应增大变异概率,通过改变种群内个体的部分基因形成新的个体,以跳出局部最优。
1.3 SPEA2方法的改进在种群更新阶段,改进后的算法只允许非支配个体加入到外部归档集
在交叉和变异阶段,事先给出比较值
| $ \left\{ \begin{gathered} K = \frac{{\sum\limits_{t = 2}^{N - 1} {U\left( {I{D_1}\left( t \right),I{D_2}\left( t \right),...,I{D_n}\left( t \right)} \right)} }}{{n \times \left( {N - 2} \right)}} 。\\ 1 \leqslant U\left( {I{D_1}\left( t \right),I{D_2}\left( t \right),...,I{D_n}\left( t \right)} \right) \leqslant n 。\end{gathered} \right. $ | (1) |
式中:
| $ \left\{ \begin{gathered} r = \frac{{\sum\limits_{t = 2}^{N - 1} {I{D_1}\left( t \right) - I{D_2}\left( t \right)} }}{{N - 2}},\\ I{D_1}\left( t \right) - I{D_2}\left( t \right) = 0,1 。\\ \end{gathered} \right. $ | (2) |
若2个个体的基因值在
本文采用大圆航线作为网格系统的参考路径扩展航路点,从出发点开始,在大圆航线上每隔距离
目标函数是反映航线质量的性能指标,是优化的最终目的。本文以船舶航行时间
| $ {\rm{min}}T = \sum\limits_{i = 1}^{n - 1} {\frac{{{S_i}}}{{{v_i}}}},$ | (3) |
| ${\rm{ min}}F = \sum\limits_{i = 1}^{n - 1} {{{\left( {{T_e}} \right)}_i}} \times {S_i}。$ | (4) |
式中:
初始种群
种群中个体质量的好坏通过适应度函数评定。SPEA2采用细粒度的适应度分配策略,在计算种群
| $ S\left( i \right) = |\{ j|j \in {P_T} + {A_T} \wedge i > j\} | ,$ | (5) |
| $ R\left( {\text{i}} \right) = \sum\limits_{j \in {P_t} + {A_t},j > i} {S(j)} 。$ | (6) |
当外部归档集
交叉通过随机选择2个个体共同经过的航路点
随着迭代步数的增加,与最大迭代次数进行比较。如果超过最大迭代次数,则终止算法,否则返回种群更新继续完成种群进化。
3 仿真实验与分析仿真实验设定的航线起点为横滨附近(35.25N,141.75E),终点为旧金山附近(37N,122W),分别在3个月份下进行多目标航线优化实验,航行环境比较结果如表1所示。
|
|
表 1 不同月份下航行环境的比较 Tab.1 Comparison of sailing conditions in different months |
船舶出发时间设定为每月6号上午11:00,选择3500 TEU的集装箱船进行仿真,其标准排水量为47202.48 t。为验证算法的性能,将本文算法与Dijkstra、NMOEA和SPEA2进行比较,其中针对3种进化算法,设定初始种群容量为34,外部种群容量6,交叉概率0.8,变异概率0.2,最大迭代次数100,求解出的Pareto前沿面如图1~图3所示。
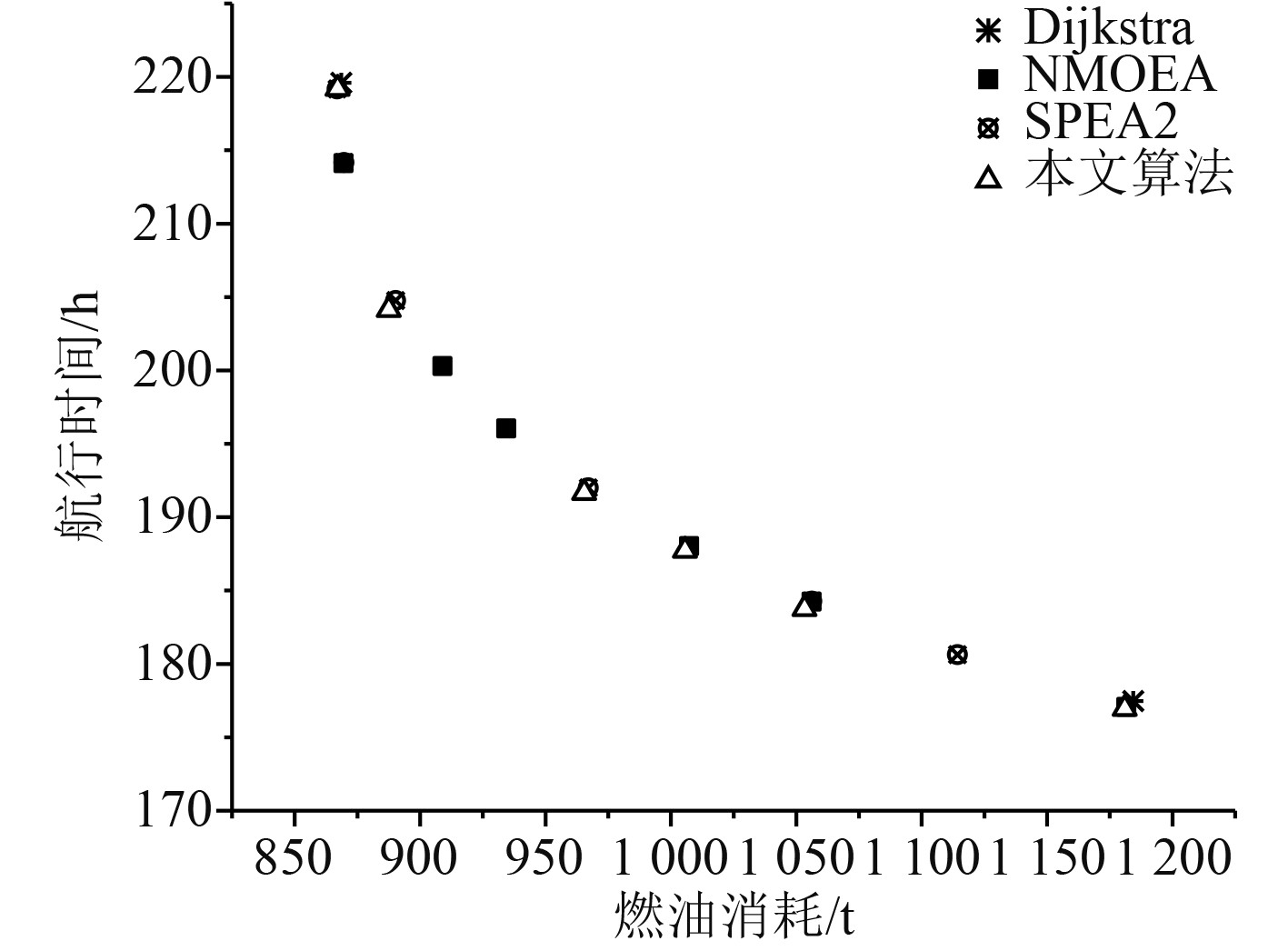
|
图 1 2018年7月的Pareto前沿面 Fig. 1 Pareto frontier in July 2018 |
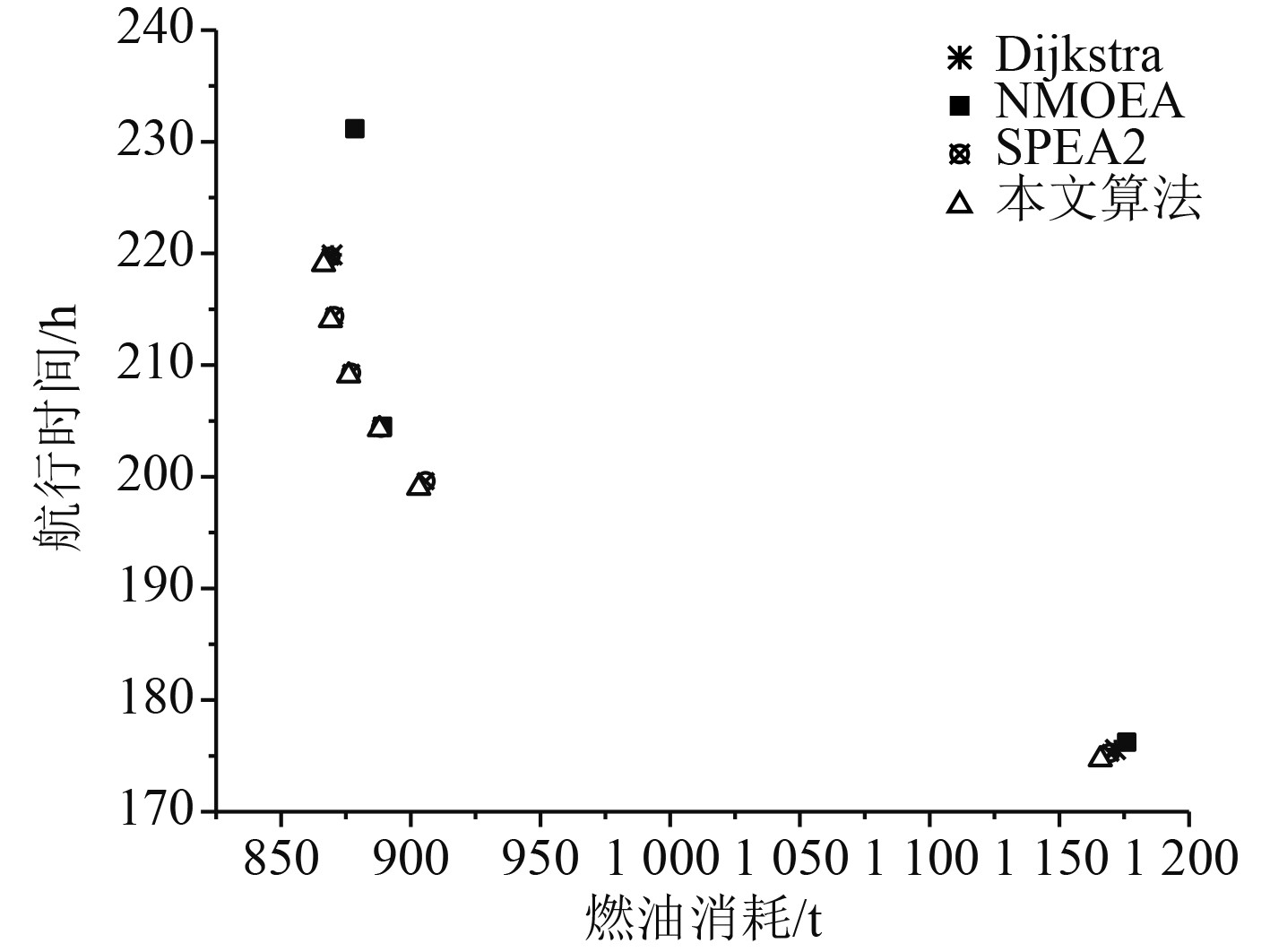
|
图 2 2018年4月的Pareto前沿面 Fig. 2 Pareto frontier in April 2018 |
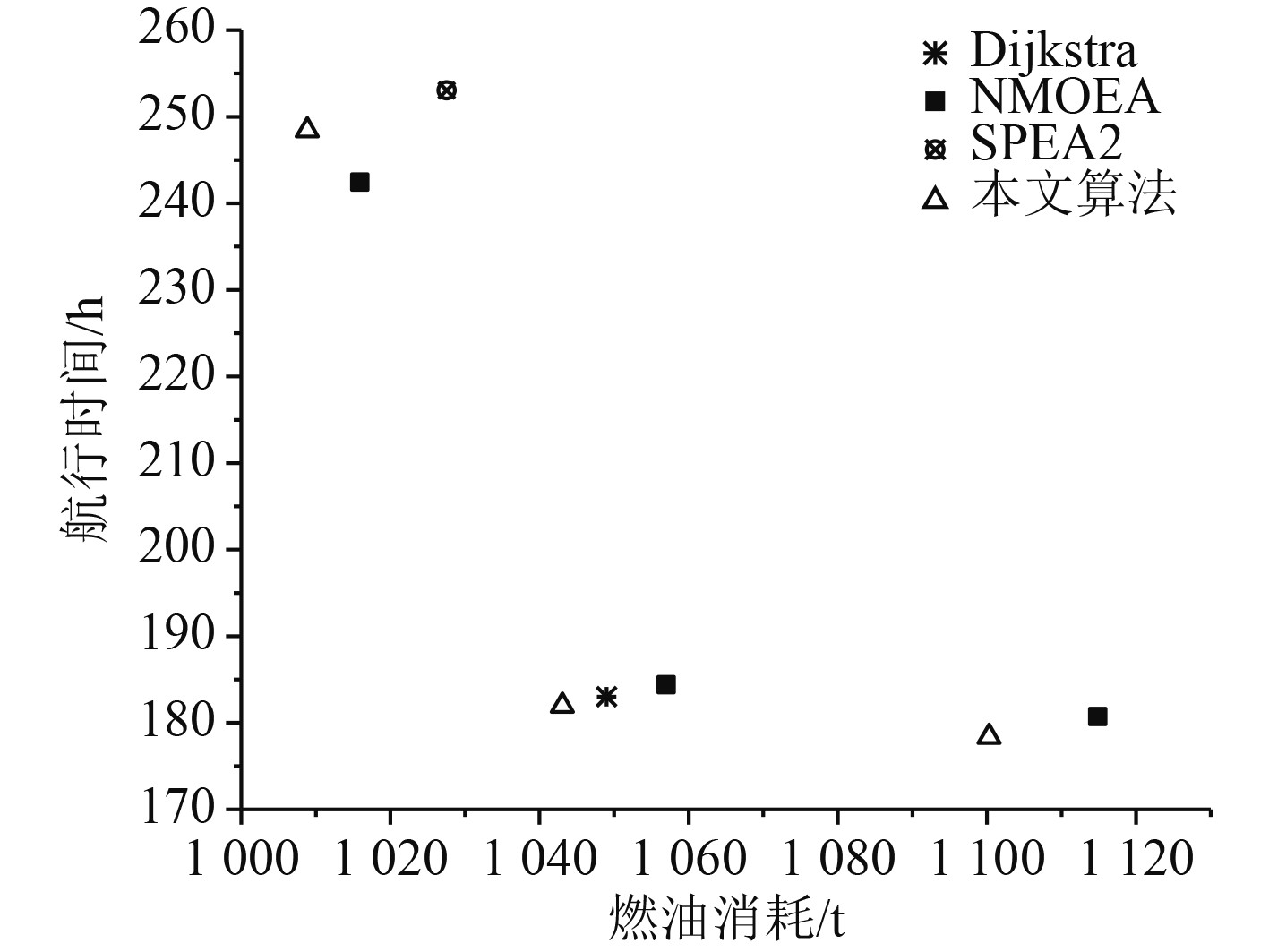
|
图 3 2018年1月的Pareto前沿面 Fig. 3 Pareto frontier in January 2018 |
实验结果显示,进化算法求得的解在时间和油耗上均优于Dijkstra算法得到的结果。另一方面,本文提出的算法在收敛性上优于NMOEA和SPEA2,且随着气象的变差,优势表现越明显。从多目标进化算法性能评价指标-超体积(HV)[9]的角度对结果进行数学分析。表2比较了3种进化算法求得解的HV值,HV值越高,群体中个体的综合表现越好。将(1120,260)作为参考点进行HV的计算,结果显示本文提出的算法综合性能最高,其次SPEA2,最差的是NMOEA。
|
|
表 2 进化算法的HV结果比较 Tab.2 Comparison of HV results of evolutionary algorithms |
图4~图6分别展示了3个月份下的Pareto航线集,对于海况较好的7月和4月,该月份下的航线集主要是以Dijkstra求得的航线为基础并对其优化。优化部分主要集中在航线的后半段,但在海况较差的1月份,它的Pareto航线集不仅包含Dijkstra的结果,还包括随机路线,这些路线光滑度较低,但在省油和省时方面仍优于Dijkstra结果。
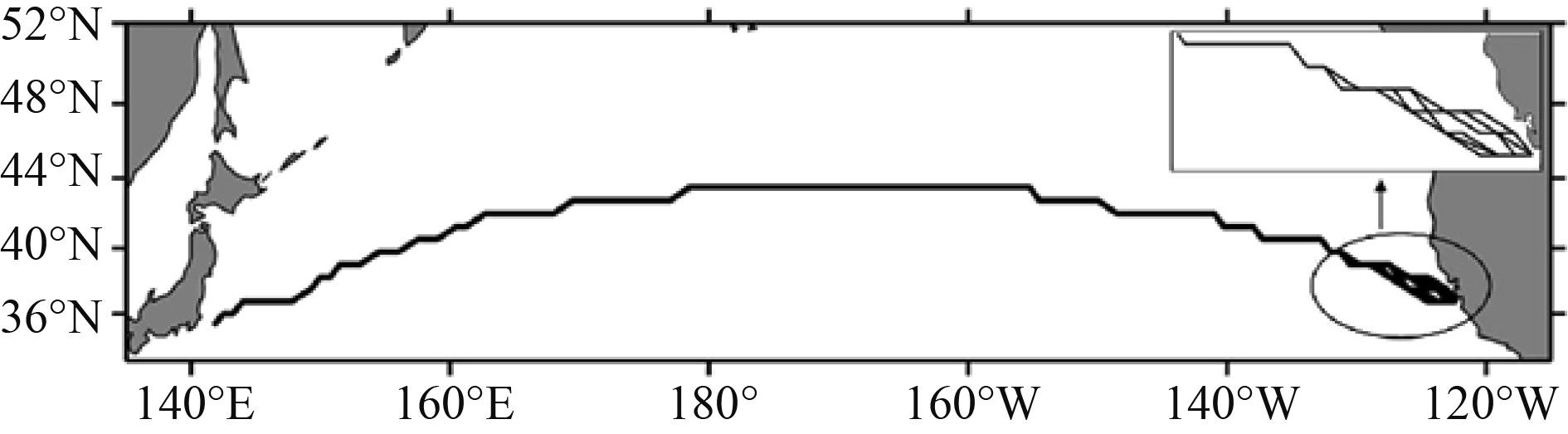
|
图 4 2018年7月的Pareto航线集 Fig. 4 Pareto route set in July 2018 |

|
图 6 2018年1月的Pareto航线集 Fig. 6 Pareto route set in January 2018 |

|
图 5 2018年4月的Pareto航线集 Fig. 5 Pareto route set in April 2018 |
针对多目标航线优化问题,本文构建了燃油成本和航行时间最小的双目标优化模型,并设计了基于SPEA2的引导性多目标进化算法。通过在初始种群中加入Dijkstra算法得到的单目标优化结果,以此作为引导,并在种群更新阶段进行改进,保证了具有代表性的精英个体继续参与进化。为避免种群优良基因的破坏以及陷入局部最优,对交叉和变异机制进行改进。最后以太平洋航线为例,在不同海况条件下进行仿真实验,验证了算法的高效性。与NMOEA和SPEA2 多目标进化算法的求解结果进行对比,证明本文算法具有较好的收敛性和全局寻优能力。
| [1] |
WALTHER L, RIZVANOLLI A, WENDEBOURG M, et al. Modeling and optimization algorithms in ship weather routing[J]. International Journal of e-Navigation and Maritime Economy, 2016, 4: 31-45. DOI:10.1016/j.enavi.2016.06.004 |
| [2] |
蒋美芝, 吕靖. 基于 Pareto 蚁群算法的船舶风险规避路径优化[J]. 交通运输系统工程与信息, 2019, 19(1): 192–199.
|
| [3] |
李鹏飞. 多目标船舶气象航线优化算法的研究与仿真[D]. 吉林: 吉林大学, 2019.
|
| [4] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: Improving the strength Pareto evolutionary algorithm[J]. TIK-report, 2001, 103.
|
| [5] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [6] |
李密青, 郑金华, 罗彪, 等. 一种基于邻域的多目标进化算法[J]. 计算机应用, 2008(6): 1570−1574.
|
| [7] |
KIM M, HIROYASU T, MIKI M, et al. SPEA2+: improving the performance of the strength pareto evolutionary algorithm 2[C]//International Conference on Parallel Problem Solving from Nature, 2004: 742–751.
|
| [8] |
LI X, WANG H, WU Q. Multi-objective optimization in ship weather routing[C]//2017 Constructive Nonsmooth Analysis and Related Topics (dedicated to the memory of VF Demyanov)(CNSA), IEEE, 2017: 1–4.
|
| [9] |
ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI:10.1109/4235.797969 |
| [10] |
VENETI A , KONSTANTOPOULOS C , PANTZIOU G.. Evolutionary computation for the ship routing problem in: Modeling[J]. Computing and Data Handling Methodologies for Maritime Transportation, 2018, 95-115. |
 2023, Vol. 45
2023, Vol. 45
