2. 海军工程大学 军用电气科学与技术研究所,湖北 武汉 430072
2. Institute of Military Electrical Science and Technology, Naval University of Engineering, Wuhan 430033, China
海战场对抗环境下水下航行器的隐身性,特别是声隐身性是其最基本和最重要的技术性能[1-3]。评估水下航行器的隐身安全性,一种常用的方法是依靠航行器壳体表面安装的振、声传感器测量得到。然而在航行器的振、声传感器数量确定之后,如何能利用有限的传感器得到更多信息,从而更精确地评估水下航行器的隐身安全性呢?这就需要进行水下航行器的传感器优化配置研究。
对于航行器壳体传感器,通常最主要且数量最多的传感器是壳体加速度传感器[4]。对于大量的加速度传感器,如何能够合理地将其布置在航行器壳体上,最大程度地采集航行器的振动信息,从而更加精确地进行声隐身安全性评估,需要认真探索。本文利用声辐射模态理论,对航行器壳体加速度传感器优化配置进行研究。
1 传感器优化配置方法及步骤近年来,国内外学者提出了声辐射模态理论[5-8]。声辐射模态及其辐射效率类似于振动问题中的主振形和固有频率。声辐射模态是矢量空间中一组相互正交的基,每组基代表一种可能的辐射形式。每一声辐射模态对应一个独立的辐射效率。声辐射模态的形状由辐射体的几何形状和振动频率决定[9]。在中、低频时,声辐射模态的辐射效率随着阶数的增加而快速降低,所以仅利用前几阶声辐射模态就能近似计算出总声功率。每一阶声辐射模态的声功率是相互独立的。利用声辐射模态理论研究声辐射问题的优势在于消除了结构模态中复杂的耦合项,使研究更简单[10-11,16-18]。
若仅针对水下航行器辐射噪声预报问题进行传感器优化配置,其目标是寻找对于辐射声功率最大的前若干阶声辐射模态进行监测,从而进行传感器位置的优化布置。然而对于水下航行器声隐身状态评估而言,并不是辐射噪声能量越大的声辐射模态,对水下航行器声隐身状态贡献也越大。因为水下航行器声隐身状态还取决于对抗方声呐的探测性能和海洋声传播损失[12]。所以,对于面向水下航行器声隐身状态评估的传感器优化配置,除了考虑声辐射模态的辐射效率外,还需考虑传播损失以及对抗方声呐在不同频率上的不同特性。基于水下航行器声隐身状态评估的艇载传感器优化配置可按照以下步骤进行:
1)确认水下航行器频谱中对声隐身状态影响最大的频率成分
进行航行器水下航行实验时,测量其辐射噪声,并针对航行器声隐身状态中最敏感的频率成分,与声呐测量和水下声传播相结合,锁定最敏感频率成分。
令航行器水下辐射噪声的线谱成分分别为
| $ st({f_i}) = \frac{{sl({f_i}) \times ds({f_i})}}{{tl({f_i}) }} i = 1,2, \cdots ,n。$ | (1) |
可表示航行器声隐身状态的安全程度,则频率
| $ {f_{st}} = \arg \max \left\{ {st\left( {{f_1}} \right),st\left( {{f_2}} \right), \cdots ,st\left( {{f_n}} \right)} \right\} 。$ | (2) |
2)将该频率按照声辐射模态进行分解,得到对声隐身状态贡献最大的前若干阶声辐射模态
在进行传感器优化配置之前,可先将传感器均匀地布置在壳体上,作为传感器初步配置方案。这样将航行器振动表面划分成若干面积相等的单元,在某频率成分各单元上的法向速度构成的向量为
| $ {{{\boldsymbol{p}}}} = {{{\boldsymbol{Zv}}}} 。$ | (3) |
其中,
| $ W = \frac{1}{2}\Delta S{{\rm{Re}}} ({{{{\boldsymbol{v}}}}^{\rm{H}}}{{\boldsymbol{p}}}) = \frac{1}{2}\Delta S{{\rm{Re}}} ({{{{\boldsymbol{v}}}}^{\rm{H}}}{{{\boldsymbol{Zv}}}}) = {{{{\boldsymbol{v}}}}^{\rm{H}}}{{{\boldsymbol{Rv}}}}。$ | (4) |
式中:
| $ W = {({{{{\boldsymbol{Q}}}}^{\rm{T}}}{{{\boldsymbol{v}}}})^{\rm{H}}}{{{{\boldsymbol{\varLambda }}}}}{{{{{\boldsymbol{Q}}}}}^{\rm{T}}}{{{{\boldsymbol{v}}}}} = {{{\boldsymbol{y}}}^{\rm{H}}}{{\boldsymbol{\varLambda y}}} = \sum\limits_{i = 1}^c {{\lambda _i}{{\left| {{y_i}} \right|}^2}} = \sum\limits_{i = 1}^c {{W_i}} 。$ | (5) |
式中,
评估共研究前
由于既考虑了声辐射功率,又考虑了海洋传播损失和对抗方声呐的探测能力,所以对于频率
3)结合传感器数量限制,针对前若干阶声辐射模态型进行传感器布置,最有效地监测这些声辐射模态
当算出前若干阶对航行器声隐身状态贡献较大的声辐射模态后,针对这些声辐射模态进行传感器优化布置。传感器优化配置时,只需将传感器按照其数量要求,来监测前若干个对航行器声隐身状态贡献较大声辐射模态。
对于这种模态已知情况下的传感器优化配置问题,国内外已经研究得较为成熟。其中常用的方法包括有效独立法、Guyan模型缩减法等。有效独立法利用Fisher信息阵使关心的模态向量尽可能线性无关,从而采集到最大的模态反应信息[13];Guyan模型缩减法通过刚度或质量子矩阵构成的转换矩阵,把那些对模态反应起主要作用的自由度保留下来作为测点的位置[14];Thomas 等[15]认为选择的测点位置应使所有模态向量的内积具有较小的余弦值。这些优化方法都能起到使测点远离各振型节点的作用,从而利用较少的传感器监测关心的模态。
利用声辐射模态理论进行面向航行器声隐身状态评估的传感器优化配置,最主要的优点在于消除了结构模态中复杂的耦合项,且在中、低频时的辐射效率随声辐射模态阶数的增加而迅速降低,少数的前几阶声辐射模态对航行器的声隐身状态有很大的贡献[16]。而本方法的难点是需事先计算出航行器的声阻抗矩阵,这是实船应用中最主要的问题。
2 仿真验证取类似水下航行器的椭球壳体结构作为研究对象,椭球模型长轴为5 m,两短轴均为1 m;结构材料密度
假设结构的激励同航行器类似存在若干种固定的激励模式,即存在有限个工况。并假定在5种常用工况下,对声隐身状态影响最大的5个频率的辐射噪声分别为:10 Hz(
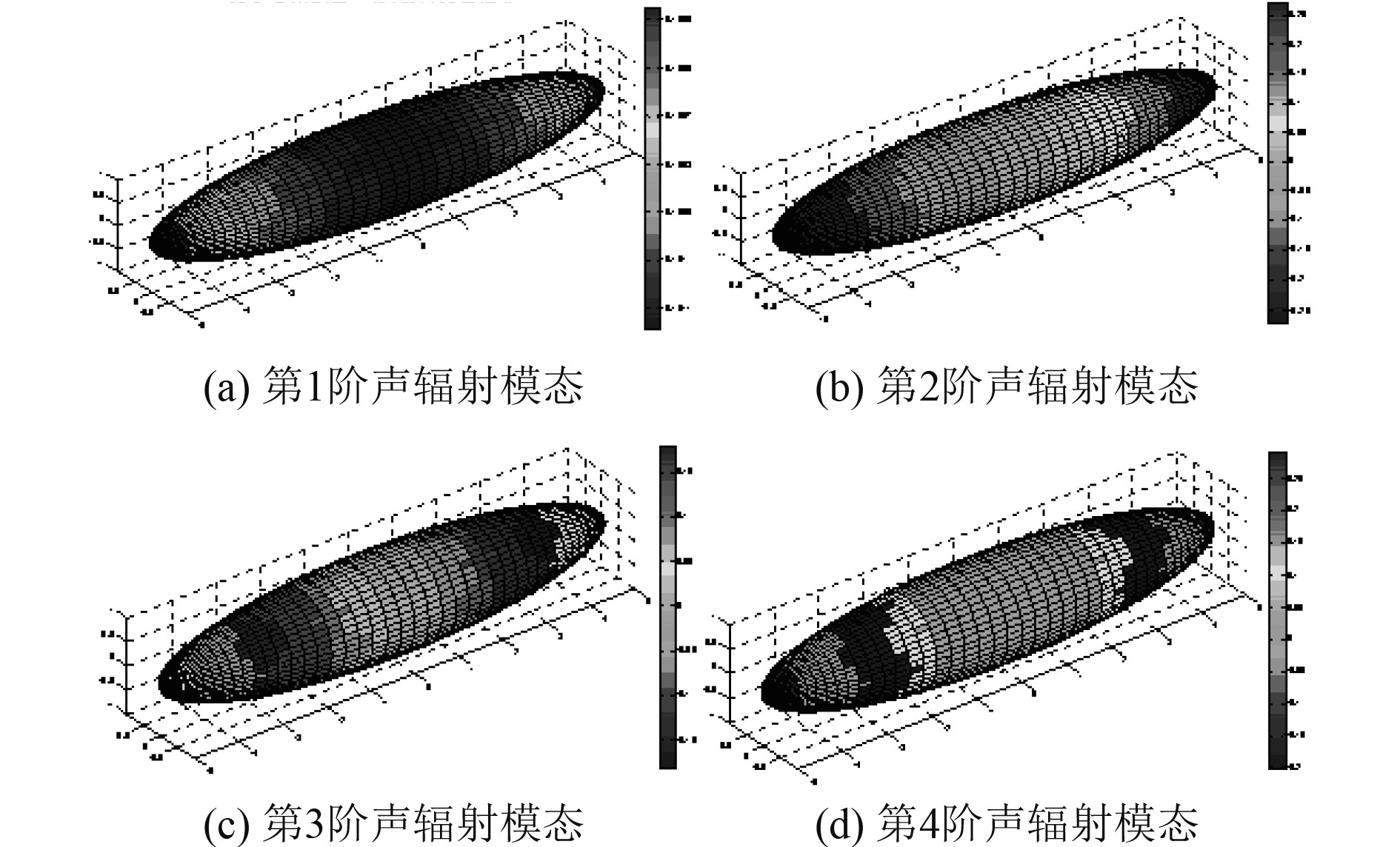
|
图 1 10 Hz时结构的前4阶声辐射模态 Fig. 1 The first 4 acoustic radiation modes of the structure in 10 Hz |
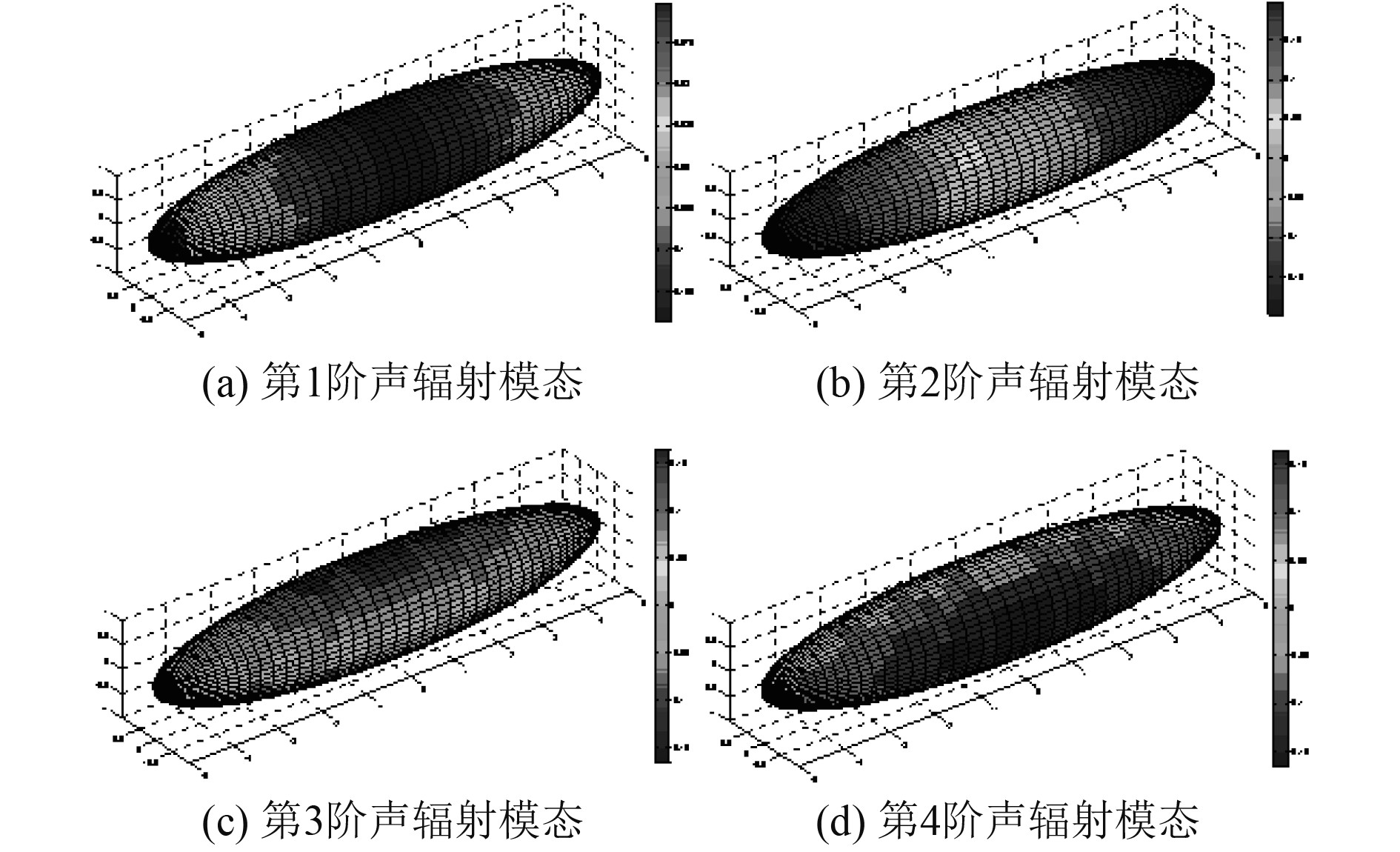
|
图 2 80 Hz时结构的前4阶声辐射模态 Fig. 2 The first 4 acoustic radiation modes of the structure in 80 Hz |

|
图 3 100 Hz时结构的前4阶声辐射模态 Fig. 3 The first 4 acoustic radiation modes of the structure in 100 Hz |

|
图 4 125 Hz时结构的前4阶声辐射模态 Fig. 4 The first 4 acoustic radiation modes of the structure in 125 Hz |
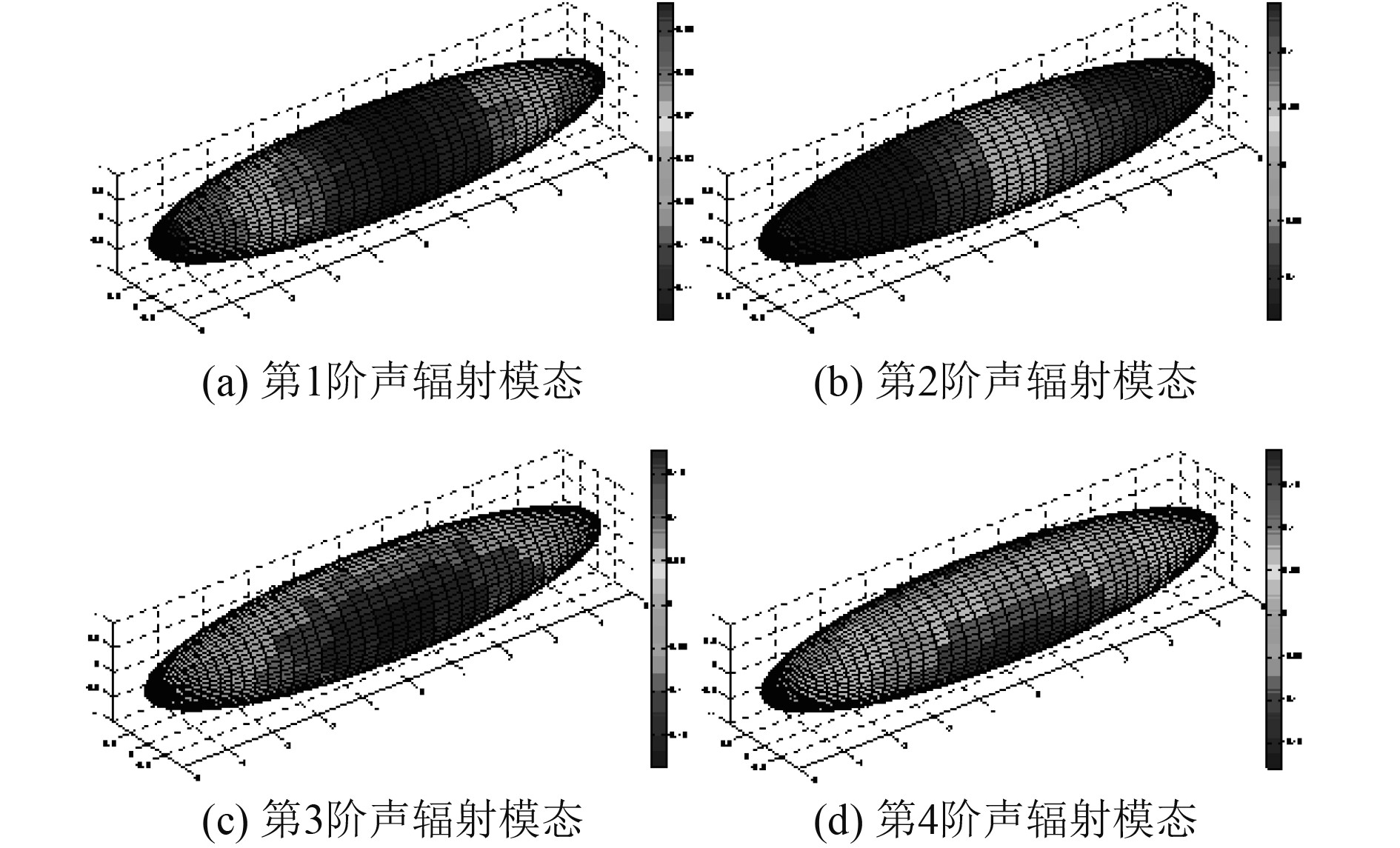
|
图 5 160 Hz时结构的前4阶声辐射模态 Fig. 5 The first 4 acoustic radiation modes of the structure in 160 Hz |
|
|
表 1 不同频率各阶声辐射模态对应的特征值 Tab.1 Eigenvalues corresponding to each acoustic radiation modes in different frequency |
可以看出,在低频(
本文针对在水下航行器壳体振动传感器数量确定的情况下,如何更好地对传感器的位置进行优化配置,以提高水下航行器声隐身状态评估准确度问题展开研究,提出了基于声辐射模态理论的传感器优化配置方法,给出了初步的优化配置方案,并通过算例分析证明了方法的实用性。
由于实际水下航行器的数据难以获取,本文算例以类似水下航行器的椭球壳体结构为研究对象,说明方法的可行性。虽然实际水下航行器结构比算例中所研究的规则椭球体结构要复杂得多,然而在低频时,可类似一个椭球壳体。本方法用于实际航行器传感器优化配置的一个主要难点在于计算航行器的声阻抗矩阵。在实际应用中,可利用有限元边界元方法进行实船建模计算,算出声阻抗矩阵后再利用本方法进行传感器优化布置,以取得更准确的航行器声隐身状态评估结果。
| [1] |
FENG X, YAN L, CHUN W. Review on vibration isolation technology[J]. Journal of Physics: Conference Series, 2021, 1820: 1-5. |
| [2] |
苏强, 王桂波, 朱鹏飞, 等. 国外潜艇声隐身前沿发展综述[J]. 舰船科学技术, 2014, 36(1): 1-9. SU Qiang, WANG Guibo, ZHU Pengfei, et al. A review of the frontier development of submarine acoustic stealth abroad[J]. Ship Science and Technology, 2014, 36(1): 1-9. DOI:10.3404/j.issn.1672-7649.2014.01.001 |
| [3] |
何琳. 潜艇隐身技术进展[J]. 舰船科学技术, 2006, 28(S2): 9-17. HE Lin. Progress in submarine stealth technology[J]. Ship Science and Technology, 2006, 28(S2): 9-17. |
| [4] |
汤智胤, 金广文, 何琳. 潜艇声隐身状态快速评估研究[J]. 振动与冲击, 2008, 27(7): 113-117. TANG Zhiyin, JIN Guangwen, HE Lin. Research on rapid evaluation of submarine acoustic stealth status[J]. Vibration and Shock, 2008, 27(7): 113-117. |
| [5] |
CURNFARE K A. The radiation modes of baffled finite plate[J]. Journal Acoustical Society of America, 1995, 98(3): 1570-1580. DOI:10.1121/1.413423 |
| [6] |
GUO Liang, ZHU Hai-chao, MAO Rong-fu, et al. Sound field separation technique based on acoustic radiation modes[J]. Journal of Ship Mechanics, 2017, 21(6): 779-790. |
| [7] |
苏俊博, 朱海潮, 毛荣富, 等. 基于声辐射模态的声场重建中的测点优化方法[J]. 振动与冲击, 2017, 36(3): 145-150. SU Junbo, ZHU Haichao, MAO Rongfu, et al. Optimization method of measurement points in sound field reconstruction based on acoustic radiation mode[J]. Vibration and Shock, 2017, 36(3): 145-150. |
| [8] |
聂永发, 朱海潮. 利用源强密度声辐射模态重建声场[J]. 物理学报, 2014(10): 256-267. |
| [9] |
聂永发, 朱海潮. 复杂结构声辐射模态的计算[J]. 应用声学, 2014, 33(6): 534-540. |
| [10] |
鱼海涛, 王英民, 王奇. 利用声辐射模态重构任意目标的散射声场[J]. 应用声学, 2017, 36(3): 264-275. DOI:10.11684/j.issn.1000-310X.2017.03.011 |
| [11] |
吴锦武, 原海朋, 毛崎波. 层合板结构声辐射模态传感器分析与测量[J]. 振动与冲击, 2016, 35(13): 26-30. |
| [12] |
汤智胤, 姜荣俊, 何琳. 潜艇声隐身态势评估方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2007, 31(1): 17-20. |
| [13] |
KAMMER D C. Sensor placements for on-orbit modal identification of large space structures[J]. Journal of Guidance, Control, and Dynamics, 1991, 14(2): 252-259. |
| [14] |
GUYAN R I. Reduction of stiffness and mass matrics[J]. AIAA Journal, 1995, 3(2): 380. |
| [15] |
THOMAS G C, CLARK R D. A modal test design strategy for modal correlation[C]//In: Proc 13th International Modal Analysis Conference. New York, 1995: 927–933.
|
| [16] |
毛崎波, 姜哲. 通过声辐射模态研究结构噪声的有源控制[J]. 江苏理工大学学报(自然科学版), 2000(4): 1-6. |
| [17] |
石炜. 矩形薄板的振动与声辐射研究及其控制[D]. 成都: 西南交通大学, 2010.
|
| [18] |
毛崎波, 姜哲. 通过声辐射模态研究结构声辐射的有源控制[J]. 声学学报, 2001(3): 277-281. MAO Qibo, JIANG Zhe. Research on active control of structural acoustic radiation through acoustic radiation modal[J]. Journal of Acoustics, 2001(3): 277-281. DOI:10.3321/j.issn:0371-0025.2001.03.015 |
 2023, Vol. 45
2023, Vol. 45
