2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063
2. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China
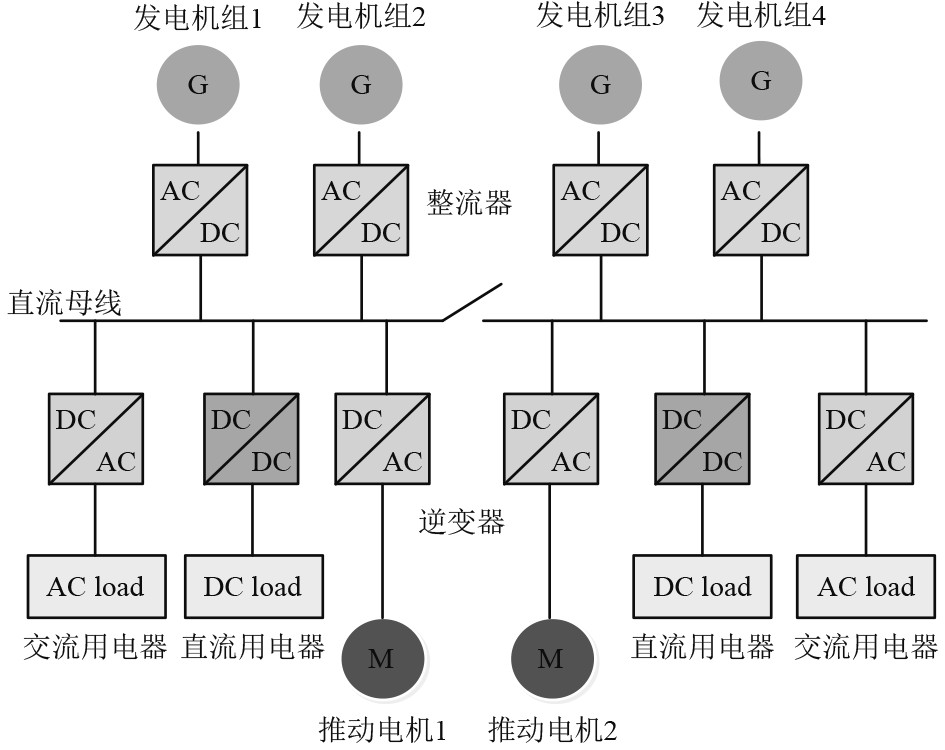
目前的船舶电力系统中,大多采用的是交流供电,该系统在能量传输过程中,存在着大量的转化级,使得变压器和滤波装置的需求也随之增大,这增加了系统功率的损耗[1]。此外,交流船舶电力系统中存在发电机并联困难、线路压降大等问题。而在中压直流电力系统中,这些问题得到了解决。船舶直流电网的典型结构如图1所示,主要由中压发电机、换流器、输电线路及负载组成。该系统不仅可以为舰船负载提供电源平台,而且能简化舰船动力系统结构、提高舰船系统效率、降低舰船噪声能级、减少舰船全寿命周期费[2]。
|
图 1 船舶直流电网的典型结构图 Fig. 1 Typical structure diagram of ship DC power grid |
从船舶直流电力系统结构图中可以看出,换流器是系统中的一个重要组成部分。目前船舶电力系统中整流器主要采用基于晶闸管结构组成,逆变器主要采用基于IGBT的全桥逆变电路组成。但随着现在船舶的电压等级不断提高,传统的换流器出现了很多新的挑战。例如,受IGBT的耐压限制,传统换流器无法用于中高压电力系统,因此,可采用MMC代替传统换流器。要使MMC在系统中稳定运行,其参数设计是一个关键问题,包括子模块个数、子模块电容及桥臂电感值,而这些参数受多种因素影响。王姗姗等[3]从系统中MMC的稳态能量交换过程,系统动态响应特性2个方面进行子模块电容值的计算,再通过系统暂态时的能量交换过程以及抑制直流双极短路故障2个方面对其进行校验。刘普等[4]通过推导桥臂电流与系统传输能量及系统运行状态之间的关系,得出流过子模块电容的电流表达式,从子模块最高电压工作限制及避免系统谐振方面考虑,对子模块电容进行设计计算。周月宾等[5]通过额定储能值的标幺化计算模型,在MMC额定储能值随调制比和功率输出范围变化规律的基础上对子模块电容量进行计算。杨立敏等[6]通过分析全桥型MMC中子模块电压呈负电平时,需要满足约束关系,推导出最优效率的交流测和直流侧的电压以及单个桥臂子模块数量的表达式。以上文献都是针对高压直流输电系统,在子模块电容的取值上主要考虑系统内部能量脉动,桥臂电感取值主要考虑避免谐振发生,但是忽略了各参数之间的相互影响。
本文针对直流母线电压为6 000 V的中压直流船舶电力系统进行研究,综合考虑各参数的限制因素,从IGBT承压等级考虑,确定子模块个数,从子模块电容电压波动率、系统有功功率响应时间、抑制系统谐振和抑制系统内部环流4个方面对子模块电容和桥臂电感值进行选取。最后通过仿真验证,确定其合理性。
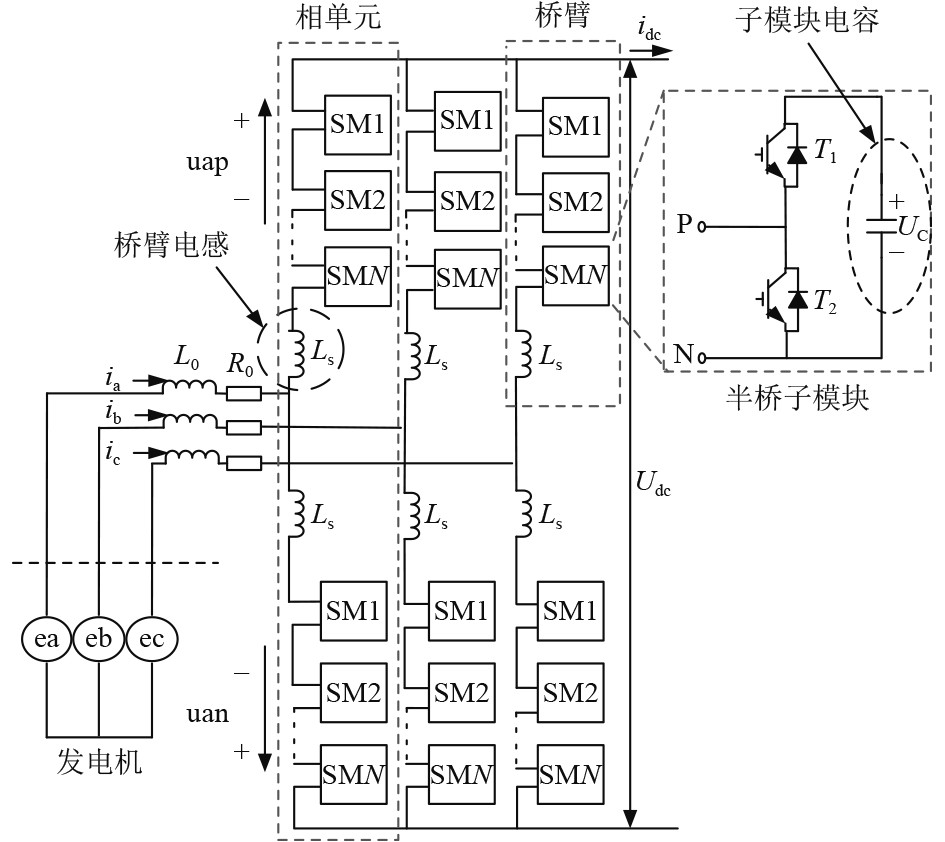
1 模块化多电平换流器模块化多电平换流器最早是由德国慕尼黑联邦国防大学的Rainer Marquardt教授于2001年提出[7],其基本结构如图2所示。
|
图 2 MMC整流器的基本结构 Fig. 2 Basic structure of MMC rectifier |
模块化多电平换流器主要是由6个桥臂构成,每个桥臂中又包含多个子模块和一个电感器,子模块有多种结构,目前最常用的是半桥子模块。半桥子模块是由2个IGBT、2个反并联二极管和1个电容器构成[8],它允许子模块的简单级联,从而简单增加输出电压电平的数量。发电机产生交流电,经过MMC整流器,通过控制其子模块的投入与切除,从而将交流电转化为直流电,传入直流母线中。
2 MMC的参数确定 2.1 子模块个数的选择子模块所能承受的电压等级是确定MMC单相桥臂子模块数量的决定性因素。通过分析MMC的工作原理可知,系统中的每个桥臂都需要具有承受全部直流电压的能力。应满足
| $ N \geqslant \frac{{{U_{dc}}}}{{{U_c}}}。$ | (1) |
可知,单个桥臂上的子模块的个数N由直流侧电压Udc和子模块电容电压的平均值Uc决定,为简化设计过程,暂时不考虑冗余度,上式均取等号。
单个子模块所能承受的电压与开关设备的额定电压有关[9]。目前IGBT耐压等级一般有:600 V、1200 V、1700 V、2500 V。如果子模块选用耐压等级为600 V的IGBT,则每个子模块最高能承受的电压为600 V,因为直流侧电压为6000 V,所以单个桥臂上至少需要10子模块,本文取N=10。
在子模块数量不是很多的情况下,MMC的电平数和子模块的个数直接相关,且满足
| $ {{{n}}_{{\rm{level}}}} = N + 1。$ | (2) |
式中:nlevel代表电平数,N为每个桥臂的子模块数量。所以可以得到,当每个桥臂子模块数量为10个时,换流器可产生11电平。
2.2 子模块电容值参数的确定 2.2.1 抑制子模块电容电压波动的电容值选取MMC在正常工作时,由于桥臂电流对子模块电容的充放电过程,会使子模块的电容电压产生波动[10]。为了让系统稳定运行,需要限制子模块电容电压的波动范围。
所有子模块平均电容电压随时间变换值uc,pa(t)可以表示为:
| $ {{{u}}_{c,pa}}(t) = \frac{{{U_{dc}}}}{N} + \Delta {u_{c,pa}}(t)。$ | (3) |
式中:
电容电压偏离其直流分量的波动范围被称为电容电压波动率,其表达式为:
| $ \varepsilon = \frac{{|\Delta {{{u}}_{{{c,pa}}}}(t)|}}{{{U_c}}} 。$ | (4) |
子模块电容储能的最大变化量为:
| $ \Delta {W_{c_0}}(m) = \frac{2}{3}\frac{{{S_V}}}{{mN\omega }}{[1 - {(\frac{{m\cos \varphi }}{2})^2}]^{3/2}}。$ | (5) |
式中:
| $ {W_{c_0,\max }}(m) = \frac{1}{2}{C_0}{[{U_{dc}}(1 + \varepsilon )]^2},$ | (6) |
| $ {W_{c_0,{\text{min}}}}(m) = \frac{1}{2}{C_0}{[{U_{dc}}(1 - \varepsilon )]^2} 。$ | (7) |
由式(7)和式(8)可以得到子模块电容的最大储能变化量为:
| $ \Delta {W_{c_0,\max }} = {W_{c_0,\max }} - {W_{c_0,\min }} = \frac{1}{2}{C_0}U_{dc}^2(4\varepsilon ) 。$ | (8) |
根据式(6)和式(9),可以得到:
| $ \varepsilon = \frac{1}{3}\frac{{{S_V}}}{{{{m}}N\omega {C_0}U_{dc}^2}}{[1 - {(\frac{{m\cos \varphi }}{2})^2}]^{3/2}} 。$ | (9) |
选取子模块的电容值时,应该考虑波动幅度最大的工况。经研究表明,当MMC满容量发无功时,子模块的电容电压波动幅度最大,此时
| $ {C_0} = \frac{1}{3}\frac{{{S_{VN}}}}{{N\omega \varepsilon U_{dc}^2}} 。$ | (10) |
当SVN=36 MW,N=10,基波角频率
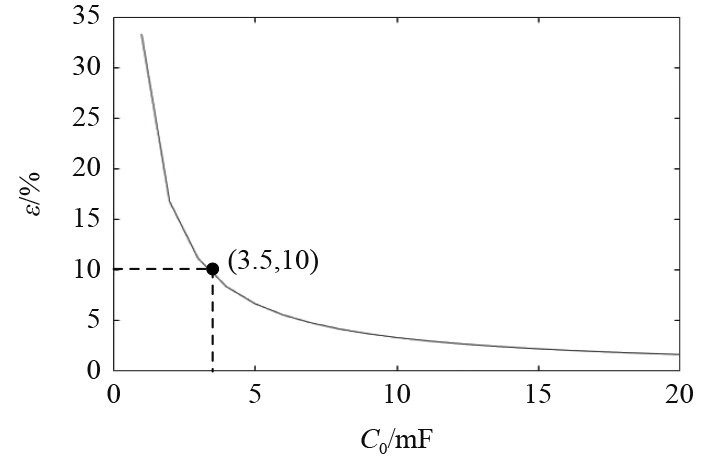
一般认为子模块电压波动率不能超过10%,由图3可知,子模块电容C0应不小于3.5 mF。
|
图 3 ε-C0曲线 Fig. 3 ε-C0 curve |
在直流输电系统中,有功功率需要通过两端换流器的协调控制来完成。系统中一端采用定直流电压控制,另一端采用定有功功率控制,后者电压需要跟随有功功率指令,假设调节时间为τ,则有
| $ {C_0} < \dfrac{{N\tau {S_{VN}}}}{{6 \cdot (\dfrac{1}{2}\Delta u_{\max }^2 + {U_{dc}}\Delta {u_{\max }})}}。$ | (11) |
式中:C为单个桥臂等效电容;
当MMC正常运行时,桥臂等效电容会随子模块的状态变化而变化,如果桥臂电感值过小,可能引发桥臂等效电容与桥臂电感发生谐振,最终导致MMC的各相桥臂电流发生畸变,放大相间环流,增大功率损耗[13]。
由电路理论知道,对于电感和电容串联电路,在串联谐振角频率
| $ {\omega _{{\text{res}}}} = \frac{1}{2}\sqrt {\frac{N}{{{L_0}{C_0}}}} 。$ | (12) |
二倍频环流谐振角频率
| $ {\omega _{{\text{cirel}}}} = \dfrac{{2\omega }}{{\sqrt {1 + \dfrac{{128{f^2}(1)}}{{3{{\text{π}} ^2}{N^2}}}} }} 。$ | (13) |
式中:
当
因为调制比m的取值范围为0 ~ 1,所以
| $ {\omega _{{\rm{cirel}}}} = 1.55\omega \sim 2\omega 。$ | (14) |
可知,有2种方案可以使得
| $ \frac{1}{2}\sqrt {\frac{N}{{{L_0}{C_0}}}} = 1.0\omega ,$ | (15) |
| $ {L_0} = \frac{N}{{4{\omega ^2}{C_0}}} 。$ | (16) |
由于MMC结构的原因,系统内部会产生相间环流。环流的存在会增大换流器上的功率损耗。一般环流分量幅值应小于桥臂电流基波分量的20%。对系统中相单元中的瞬时功率进行积分,就能得到其中电容的储能表达式,经过分析可以得到,MMC系统中相单元中存在的环流主要是二倍频且为负序性质的[13],其峰值大小为:
| $ {I_{2f}} = \frac{{{S_{VN}}}}{3}\frac{1}{{8{\omega ^2}{C_0}{L_0}{U_c} - {U_{dc}}}} 。$ | (17) |
式中:P为系统中的有功功率;ω为交流侧基波角频率;C0为子模块电容值;Uc为子模块电容电压;Udc为直流侧电压。
由此得到桥臂电感值与二倍频环流峰值的关系式为:
| $ {L_0} = \dfrac{1}{{8{C_0}{\omega ^2}{U_{dc}}}}\Bigg(\frac{{{S_{VN}}}}{{3{I_{2f}}}} + {U_{dc}}\Bigg) 。$ | (18) |
为验证上述结论,按照图1的结构,在Matlab/Simulink中搭建三相MMC模型,其参数如表1所示。
|
|
表 1 MMC建模参数 Tab.1 MMC modeling parameters |
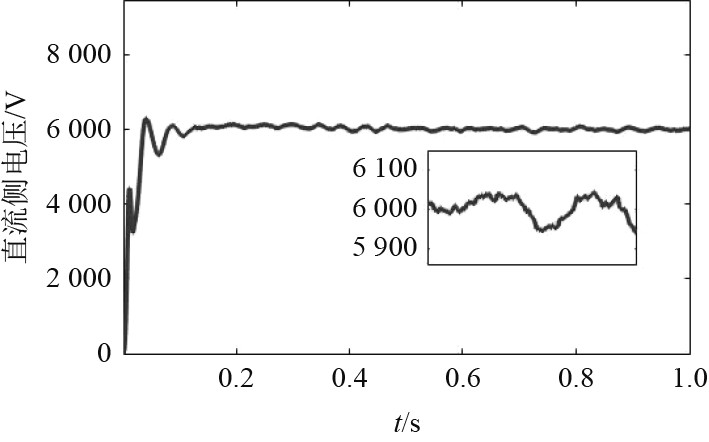
从经济性的角度考虑,子模块电容选取3.5 mF,此时如果从抑制系统谐振的角度考虑,由式(16)可知,桥臂电感值应不小于7.5 mH,而从抑制系统内部环流的角度考虑,由式(18)可知,桥臂电感应不小于24 mF。取桥臂电感值为24 mF。仿真得到的直流侧电压如图4所示。
|
图 4 直流侧电压 Fig. 4 DC side voltage |
可知,当直流侧电压稳定时,直流电压波动位100 V左右,即波动率为1.67%,系统稳定性良好。
为了进行比较,对子模块电容值取不同值。图5~图10分别是当子模块电容电压取3mF、3.5 mF、4 mF时的子模块电容电压和对应的谐波含量图。
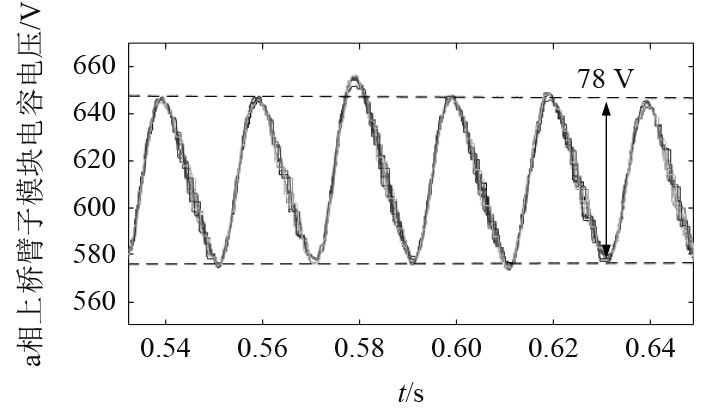
|
图 5 子模块电容值为3 mF的电容电压 Fig. 5 Capacitance voltage with 3 mF capacitance value of sub module |
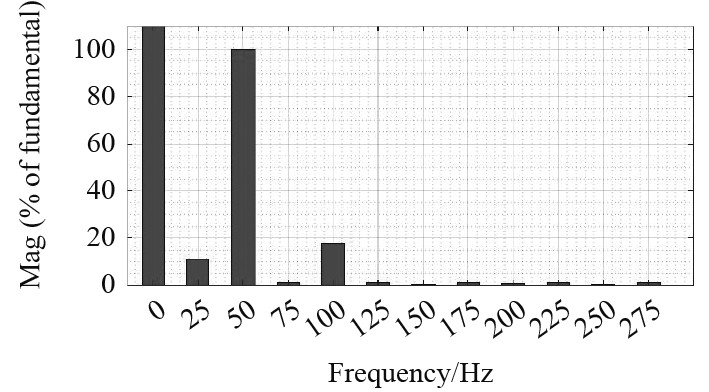
|
图 6 子模块电容值为3 mF的电容电压谐波含量 Fig. 6 Harmonic content of capacitor voltage with capacitance value of 3 mF in sub module |
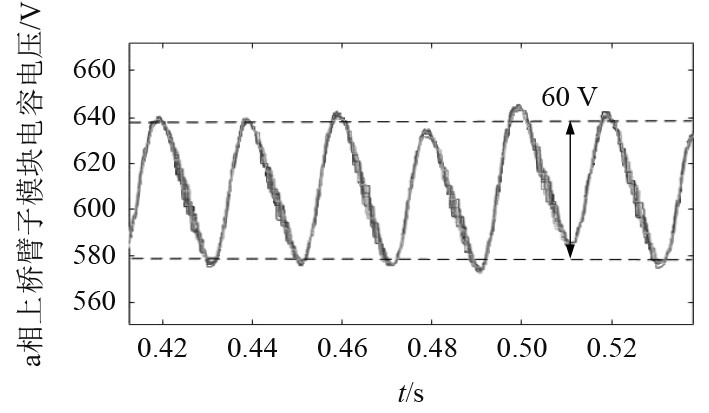
|
图 7 子模块电容值为3.5 mF电容电压 Fig. 7 Capacitance voltage with 3.5 mF capacitance value of sub module |
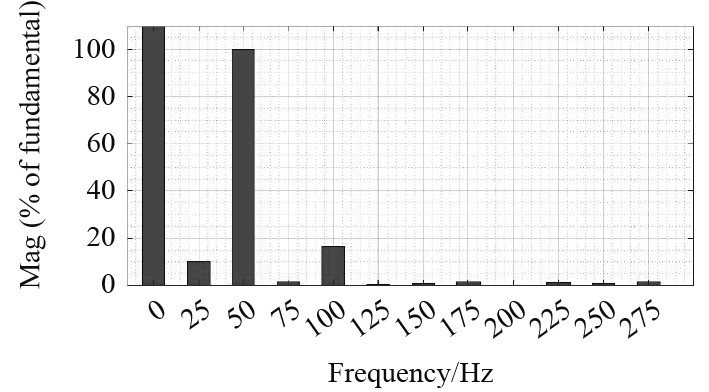
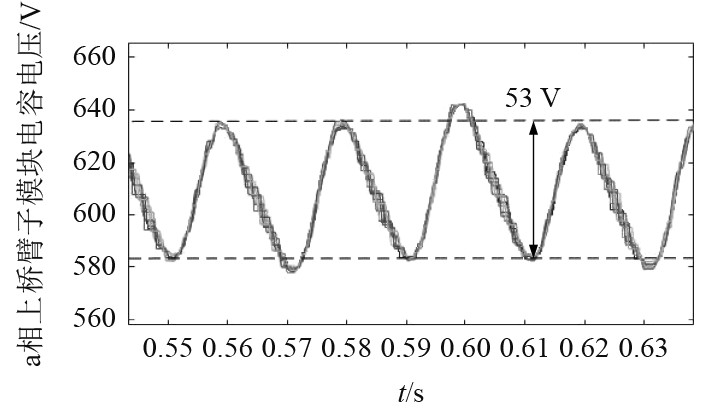
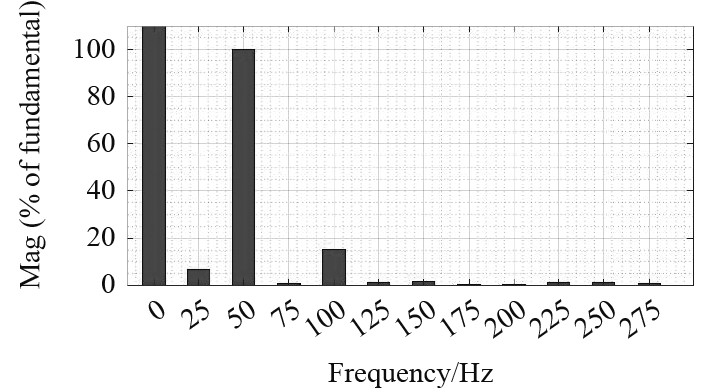
分析可知,当子模块电容值取3 mF时电压波动幅度为78 V,波动率为13%,对应的总谐波系数THD=19.72%。当子模块电容值取3.5 mF时,电压波动幅度为60 V,波动率为10%,对应的总谐波系数THD=18.92%。当子模块电容值取4 mF时,电压波动幅度为53 V,波动率为8.8%,对应的总谐波系数THD=17.86%。
仿真得到的a相上下桥臂电流如图11所示。
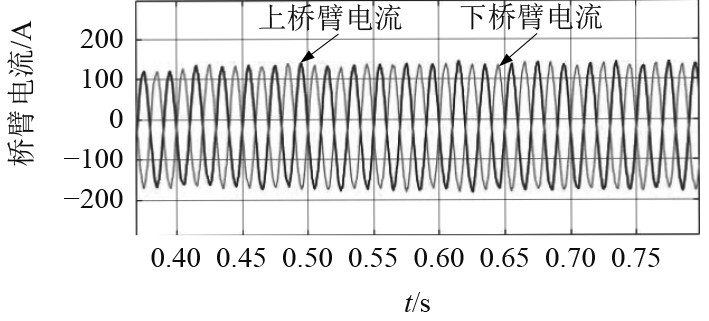
|
图 11 a相上下桥臂电流 Fig. 11 Phase a upper and lower bridge arm current |
为了分析电感值对环流的影响,分别取不同的电感值,图12和图13分别为桥臂电感取7.5 mH和24 mH时的二倍频环流图像。
|
图 8 子模块电容值为3.5 mF的电容电压谐波含量 Fig. 8 Harmonic content of capacitor voltage with capacitance value of 3.5 mF in sub module |
|
图 9 子模块电容值为4 mF的电容电压 Fig. 9 Capacitance voltage with 4 mF capacitance value of sub module |
|
图 10 子模块电容值为4 mF的电容电压谐波含量 Fig. 10 Harmonic content of capacitor voltage with capacitance value of 4 mF in sub module |
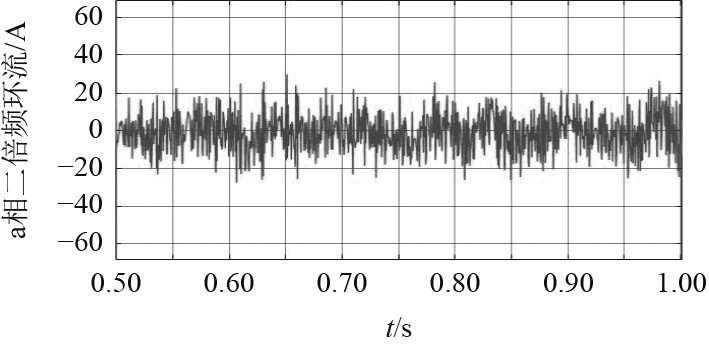
|
图 12 桥臂电感为7.5 mH时二倍频环流 Fig. 12 Double frequency circulating current when the bridge arm inductance is 7.5 mH |

|
图 13 桥臂电感为24 mH时二倍频环流 Fig. 13 Double frequency circulating current when the bridge arm inductance is 24 mH |
由图11和图12可知,桥臂电感为7.5 mH时,二倍频环流的峰值为50 A左右,当桥臂电感为24 mH时,二倍频环流峰值为14 A左右。
4 结 语本文介绍中压直流船舶电力系统,并为用于直流电压为6000 V的电力系统的模块化多电平换流器的参数进行设计,包括子模块数量、子模块电容值和桥臂电感值。最后在Matlab/Simulink平台上搭建仿真模型,验证参数的合理性。得到如下结论:
1)用模块化多电平换流器代替传统换流器在中压船舶电力系统使用时,直流侧电压在达到稳定后,波动非常小,满足船舶电力系统的需求。
2)子模块电容值越大,稳定运行时它的电压波动率越小,并且谐波含量也会降低,但是成本会越高,体积也会越大。在考虑经济性条件下,该系统的子模块电容值取3.5 mF左右较为合适。
3)桥臂电感值对系统谐振和内部二倍频环流有影响。在满足约束条件下,该电力系统中桥臂电感值应取24 mH左右。
| [1] |
廖鹏, 戴瑜兴, 毕大强. 基于MMC的船舶中压直流电力系统控制策略的研究[J]. 船电技术, 2019, 39(7): 54-57+61. LIAO Peng, DAI Yuxing, BI Daqiang. Research on control strategy of ship MV DC power system based on MMC[J]. Ship Power Technology, 2019, 39(7): 54-57+61. |
| [2] |
马伟明, 王东, 马凡. 舰船动力的革命——综合电力系统[J]. 科技纵览, 2019(9): 54–57. MA Weiming, WANG Dong, MA Fan. Revolution of ship power - integrated power system [J]. Overview of Science and Technology, 2019 (9): 54–57 |
| [3] |
王姗姗, 周孝信, 汤广福, 等. 模块化多电平HVDC输电系统子模块电容值的选取和计算[J]. 电网技术, 2011, 35(1): 26-32. WANG Shanshan, ZHOU Xiaoxin, TANG Guangfu, et al. Selection and calculation of sub module capacitance of modular multi-level HVDC transmission system[J]. Power Grid Technology, 2011, 35(1): 26-32. |
| [4] |
刘普, 王跃, 雷万钧. 抑制模块化多电平变流器谐振的子模块电容参数设计方法[J]. 中国电机工程学报, 2015, 35(7): 1713-1722. LIU Pu, WANG Yue, LEI Wanjun. Design method of sub module capacitance parameters for restraining resonance of modular multilevel converter[J]. Chinese Journal of Electrical Engineering, 2015, 35(7): 1713-1722. |
| [5] |
周月宾, 宋强, 杨柳, 等. 模块化多电平换流器电容用量的标幺化分析与设计方法[J]. 电力建设, 2021, 42(11): 1-12. ZHOU Yuebin, SONG Qiang, YANG Liu, et al. Standardized analysis and design method for capacitor consumption of modular multilevel converter[J]. Power Construction, 2021, 42(11): 1-12. |
| [6] |
杨立敏, 朱艺颖, 孙栩. 基于损耗分析的全桥型MMC参数优化设计[J]. 电力自动化设备, 2020, 40(3): 128-133. YANG Limin, ZHU Yiying, SUN Xu. Parameter optimization design of full bridge MMC based on loss analysis[J]. Power Automation Equipment, 2020, 40(3): 128-133. |
| [7] |
蔡思烨, 姜建国, 李洪亮. 改进的MMC子模块电容参数设计和均压方法[J]. 电力电子技术, 2019, 53(3): 25-29. CAI Siye, JIANG Jianguo, LI Hongliang. Improved capacitor parameter design and voltage sharing method of MMC sub module[J]. Power Electronics Technology, 2019, 53(3): 25-29. |
| [8] |
方田, 李化, 李征, 等. 柔性直流输电中子模块电容参数设计及其寿命终结判据[J]. 电力电容器与无功补偿, 2020, 41(4): 57-62. FANG Tian, LI Hua, LI Zheng, et al. Capacitance parameter design and end of life criteria for sub modules of flexible DC transmission[J]. Power Capacitor and Reactive Compensation, 2020, 41(4): 57-62. |
| [9] |
蔡婷婷, 刘宿彤. 基于数学分析的抑制模块化多电平换流器电压波动的子模块电容参数设计[J]. 电测与仪表, 2019, 56(8): 16-22. CAI Tingting, LIU Sutong. Sub module capacitance parameter design based on mathematical analysis to suppress voltage fluctuation of modular multilevel converter[J]. Electrical Measurement and Instrumentation, 2019, 56(8): 16-22. |
| [10] |
KANG J, KANG D W, LEE J P. Design procedure of MMC-HVDC system: comprehensive consideration of internal and external dynamics[J]. IEEE Access, 2020, 8: 157437-157450. DOI:10.1109/ACCESS.2020.3018597 |
| [11] |
肖晃庆. MMC型柔性直流电网建模、分析与控制研究[D]. 杭州: 浙江大学, 2018.
|
| [12] |
徐政, 肖晃庆, 张哲任. 模块化多电平换流器主回路参数设计[J]. 高电压技术, 2015, 41(8): 2514-2527. XU Zheng, XIAO Huangqing, ZHANG Zheren. Parameter design of main circuit of modular multilevel converter[J]. High Voltage Technology, 2015, 41(8): 2514-2527. |
| [13] |
李卫国, 秦敬明, 陈璟毅, 等. MMC-HVDC系统子模块电容与桥臂电感的选取和计算[J]. 东北电力大学学报, 2019, 39(2): 47-53. LI Weiguo, QIN Jingming, CHEN Jingyi, et al. Selection and calculation of capacitance and bridge arm inductance of MMC-HVDC system sub module[J]. Journal of Northeast Electric Power University, 2019, 39(2): 47-53. DOI:10.19718/j.issn.1005-2992.2019-02-0047-07 |
| [14] |
徐政. 柔性直流输电系统[M]. 北京: 机械工业出版社, 2016: 64–68.
|
 2023, Vol. 45
2023, Vol. 45
