0 引　言

无人机具有生存能力强、机动性能好、飞行环境要求低等优点，广泛应用于空中侦察、战场监视、远程打击等，在现代海军装备中，舰载无人机能够有效避免不必要的人员伤亡^[1]。无论民用领域还是军工领域应用均具有广阔前景，随之出现自动起落以及自动执行任务无人机，为了配合无人机自动起落，需要系统配备可供无人机起落的地面站，无人机识别定位技术成了无人机自动精准降落技术的重点所在^[2-3]。

本文基于图像处理方法，采用“地对空”的方式捕捉无人机位置，并对无人机进行引导，实现无人机识别定位。其工作流程大致为：地面站摄像头首先采集地面站处背景图片，并对该图片进行相应的处理，待后续提取无人机使用；待无人机进入视野，受到引导请求之后，拍摄无人机图片并进行相应处理，与之前背景差图片作差以提取无人机；将背景差图像应用最大类间方差法进行二值化处理；对该二值化图像进行霍夫变换，将符合条件的点通过霍夫直线变换变换到霍夫空间，对霍夫空间的点进行统计，得到图像空间直线的极坐标表示；对符合条件的极坐标点按正交关系进行分类，剔除无用的点，并进行坐标反变换将极坐标变换成图像空间的直线，通过计算2条直线相交点来确定无人机在图像中的坐标。该方法将摄像头置于地面站中心，拍摄无人机照片，并识别无人机在图像中的位置，进一步计算无人机相对于地面站的方位与距离，从而达到无人机精准降落的目的。

本文首先介绍背景差原理，并应用此原理将无人机与背景图像分离；然后介绍最大类间方差法及其原理，从原理入手将背景差图像处理成可用于霍夫变换二值化图像。从二值化图像出发，对霍夫直线变换进行详细分析，并将其应用到上述二值化图像，得到检测出无人机中心位置的算法，为无人机的精准降落提供技术基础。

1 无人机图像提取处理

从图像识别入手，将摄像头放置在舰船甲板地面站，通过拍摄无人机方式定位，并以无线通信方式发送其位置到无人机，作为无人机调节位置的反馈，以达到无人机精准降落目标。背景差法是目前针对运动物体检测的常用方法之一，将2幅图片抽象为像素矩阵，矩阵元素相减，得到2个矩阵差分矩阵，即是2幅图片进入背景图中物体图片。当被检测目标进入背景时，采集到的图像与背景之间便在物体周围产生差值，通过两者作差即可提取出该物体，实现物体与背景分离的目的^[4]。

1.1 背景分离预处理

背景差法是对像素作差，要求像素点表征该像素颜色深度信息。由于拍摄到的图片为RGB三通道BMP格式图像，因此对图片进行背景作差之前需要将其转化为单通道灰度图^[5]。

对于RGB空间数据，可以通过相应公式将其归一化到灰度空间，常用的灰度值计算公式有：

$ GRAY = {({R^{2.2}}\times 0.2126 + {G^{2.2}}\times0.7152 + {B^{2.2}}\times0.0722)^{\frac{1}{{2.2}}}} ，$

(1)

$ GRAY = {({R^{2.2}}\times0.2973 + {G^{2.2}}\times0.6274 + {B^{2.2}}\times0.0753)^{\frac{1}{{2.2}}}}。$

(2)

式中：R为红色数据，G为绿色数据，B为蓝色数据。式（1）为简化的sRGB IEC61966-2.1 [ $\gamma $ =2.20]公式，式（2）为Adobe RGB (1998) [ $\gamma $ =2.20]公式。对于本文系统，由于计算速度的需要，可以将式（2）简化为简单的乘法运算：

$ GRAY = R\times 0.299 + G\times 0.587 + B\times 0.114。$

(3)

进一步，可以将式(3)简化为移位运算：

$ GRAY = (R\times 38 + G\times 75 + B\times 15) > > 7 。$

(4)

式中：R为红色数据；G为绿色数据；B代表蓝色数据。

由式（4）将RGB彩色图像处理成灰度图，如图1所示。转化而来的灰度图像会保留原图像色度信息，无人机与背景差异明显，为无人机与背景的分离打下良好基础。

1.2 背景差图像处理

图像阈值自动选取选择使用最大类间方差法。能够很好地保留图像的边缘信息，避免过度分割，分割效果理想。地面站在收到无人机返航请求时会先拍摄一张背景图片。当无人机降落时，地面站会在收到引导请求后拍摄一张无人机在当前视野中的图片，通过对当前图片与背景图片的差分，实现无人机与背景的分离^[6]。

1.2.1 最大类间方差法算法原理

对于被检测目标图像 ${{{I}}_{(x,y)}}$ 前景和背景分割阈值记为T，属于前景像素点数占整幅图像比例记为 $ {\omega _0} $ ，其平均灰度 ${\mu _0}$ ；背景像素点数占整幅图像比例为 ${\omega _1}$ ，其平均灰度为 ${\mu _1}$ 。图像的总平均灰度记为 $\mu $ ，类间方差记为g。

假设图像背景较暗，并且图像大小为M×N，图像中像素的灰度值小于阈值T的像素个数记作 ${N_0}$ ，像素灰度大于阈值T的像素个数记作 ${N_1}$ ，则有:

$ {\omega _0} = \frac{{{N_0}}}{{M\times N}}，\qquad {\omega _1} = \frac{{{N_1}}}{{M\times N}}，$

$ {N_0} + {N_1} = M\times N ，\qquad \omega o + {\omega _1} = 1，$

$ \mu = {\omega _0}\times {\mu _0} + {\omega _1}\times {\mu _1}，$

$ g = {\omega _0}\times {({\mu _0} - \mu )^2} + {\omega _1}\times{({\mu _1} - \mu )^2} 。$

得到等价公式： $g = {\omega _0}\times {\omega _1}\times{({\mu _0} - {\mu _1})^2}$ 。

基于遍历方法得到使类间方差最大阈值T，即为所求。

1.2.2 算法处理图像实现

最大类间方差法实现过程如下：设待分割图像为 $f(x)$ ，图像的灰度变化范围为[0, L-1]， ${n_i}$ 为灰度为 $ i $ 的像素数目， $ N $ 为图像的总像素数， $N = \displaystyle\sum\limits_{i = 0}^{L - 1} {{n_i}} $ ， ${p_i}$ 为灰度级出现的概率，门限 $ t $ 将图像划分为： ${C_0} = \{ 0, 1......, t\} $ ， ${C_1} = \{ t + 1,......,L - 1\} $ ，若 $f(x) < t$ ，则 $(x,y) \in {C_0}$ ；若 $f(x) > t$ ，则 $(x,y) \in {C_1}$ 。对图像的直方图进行归一化得到灰度级的概率分布： $ {p_i} = \dfrac{{{n_i}}}{N} $ ， ${p_i} \geqslant 0$ ， $\displaystyle\sum\limits_{i = 0}^{L - 1} {{p_i}} = 1$ 。

$ {C}_{0}、{C}_{1} $ 类出现的概率为：

$ {p_0}(t) = \displaystyle\sum\limits_{i = 0}^t {{p_i}} ，{p_1}(t) = \displaystyle\sum\limits_{i = t + 1}^{L - 1} {{p_i}}。$

均值分别为： $ {u_0}(t) = \displaystyle\sum\limits_{i = 0}^t {\frac{{i{p_i}}}{{{p_0}(t)}}} $ ， ${u_1}(t) = \displaystyle\sum\limits_{i = t + 1}^{L - 1} {\dfrac{{i{p_i}}}{{{p_1}(t)}}} $ 。

图像总体灰度值为： $ UT = \displaystyle\sum\limits_{i = 0}^{L - 1} {i{p_i}} = {p_0}{u_0} + {p_1}{u_1} $ 。

由公式可求得 $ {C}_{0}、{C}_{1} $ 的方差为：

$ {\delta _0}^2 = \sum\limits_{i = 0}^t {\frac{{{{(i - {u_0})}^2}{p_i}}}{{{p_0}}}}，{\delta _1}^2 = \sum\limits_{i = t + 1}^{L - 1} {\frac{{{{(i - {u_1})}^2}{p_i}}}{{{p_1}}}} 。$

定义类间方差为：

$ {\delta _j}^2(t) = {p_0}{({u_0} - {u_T})^2} + {p_1}{({u_1} - {u_T})^2}。$

定义类内方差为：

$ {\delta _i}^2(t) = {p_0}{\delta _0}^2 + {p_1}{\delta _1}^2 。$

定义总体方差为：

$ {\delta _T}^2(t) = \sum\limits_{i = 0}^{L - 1} {{{(i - {u_T})}^2}{p_i}}。$

三者有关系：

$ {\delta _T}^2 = {\delta _i}^2 + {\delta _j}^2。$

式中： ${\delta _i}^2$ 、 ${\delta _j}^2$ 为门限 $ t $ 的函数， ${\delta _T}^2$ 与t无关，通过最大化类间方差 ${\delta _j}^2$ 确定图像的最佳阈值 $ T $ ，即

$T = \arg \max {\delta _j}^2 = \arg \max [{p_0}(t){({u_0} - {u_T})^2} + {p_0}(t){({u_0} - {u_T})^2}] 。$

由此，即可得到计算一幅图像二值化阈值的算法实现。应用该算法处理得到的图片如图2所示。白色为无人机，黑色为背景。可见，应用OTSU算法可以正确地实现无人机与背景的分割。

2 无人机识别定位 2.1 霍夫直线变换算法原理

霍夫变换(Hough transform)在图像处理中进行特征提取，将图像空间点变换为霍夫空间，并对霍夫空间中点进行累加，累计结果局部最大值将得到一个符合特定形状的集合，霍夫变换目前可用于任意形状物体的识别^[7]。

一条直线在笛卡尔坐标系中可由参数斜率和截距 $(m,b)$ 表示，在极坐标系下由参数极径和极角 $(r,\theta )$ 表示。已知直线在笛卡尔坐标系中的表达式为：

$ y = mx + b 。$

变换到其极坐标系表示：

$ y = - \dfrac{{\cos \theta }}{{\sin \theta }}x + \dfrac{r}{{\sin \theta }} 。$

化简可以得到： $ r = x\cos \theta + y\sin \theta $ 。

对于直角坐标系中的点 $({x_0},{y_0})$ ，可以将通过这个点的一族直线统一定为：

$ r = {x_0}\cos \theta + {y_0}\sin \theta。$

在极坐标系下，每一对 $\left( {{r_\theta },\theta } \right)$ 值代表直角坐标系下一条通过点 $({x_0},{y_0})$ 的直线。

霍夫变换将图像空间中符合条件的点变换到极坐标系，将极坐标系离散化，通过追踪图像空间每个点对应曲线的交点，交点曲线数目超过阈值，代表参数对 $\left( {{r_\theta },\theta } \right)$ 在图像空间中是一条直线。将极坐标 $\left( {{r_\theta },\theta } \right)$ 代入即可得出原图像中直线，进而将其绘制在原图像中。根据算法原理进行检测图像中直线，霍夫直线检测具体的实现流程如图3所示。

应用霍夫直线变换检测到的直线如图4所示。

图4中最长30条直线所在位置，全部位于无人机旋翼臂附近，发散情况因旋翼大小及摇摆方向而有所差异，均在可接受范围内。

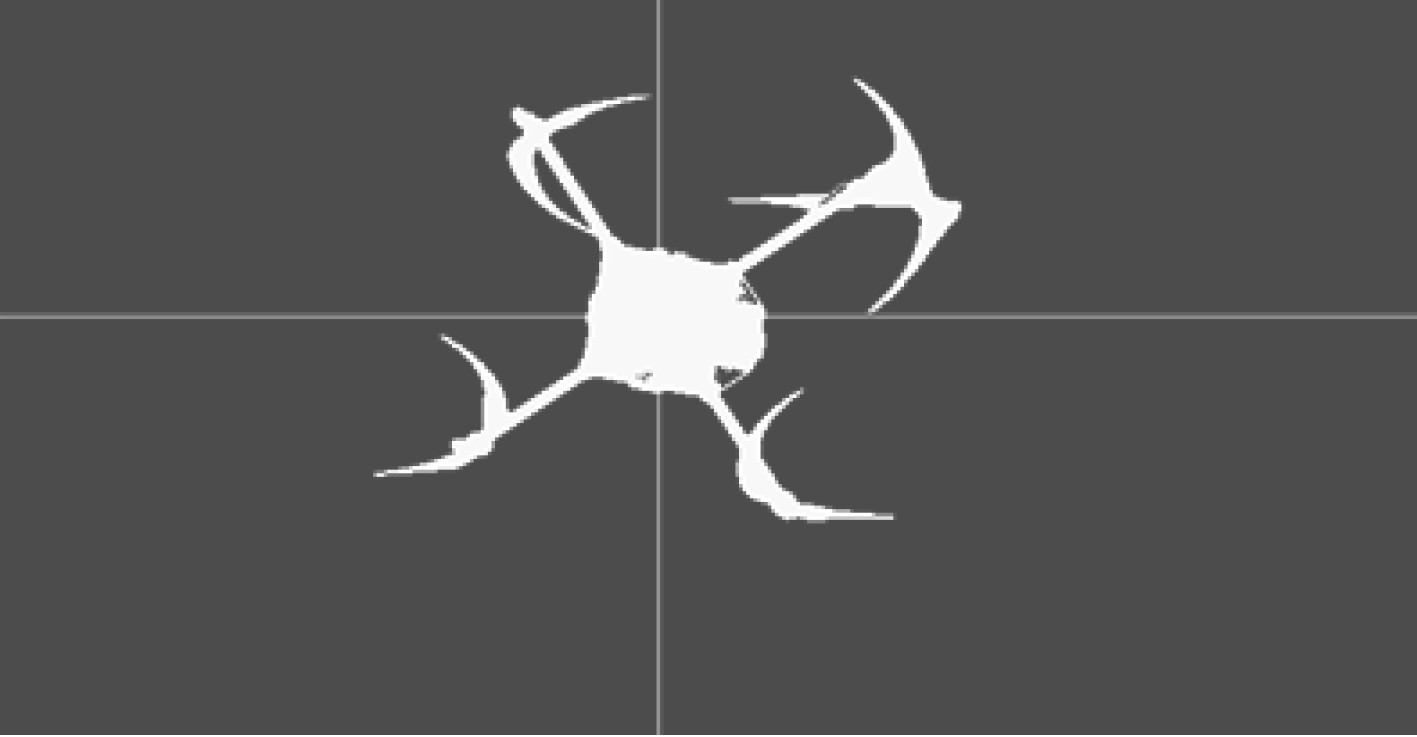
2.2 无人机位置确定

根据极坐标确定无人机位置，设定一个阈值，若落在该阈值里面的一族直线 $\theta $ 值与另一族直线 $\theta $ 值相差1/2个霍夫空间宽度，则可认为这2族直线正交。舍去阈值之外的 $\left( {r,\theta } \right)$ 参数对，对阈值之内的2族参数对 $\left( {r,\theta } \right)$ 分别取平均，得到2对参数 $({r_1},{\theta _1})$ 和 $({r_{2,}}{\theta _2})$ ，分别对应图像空间中一条直线。将该参数对代入便可以得到2条直线的解析表达式，2条直线的交点 $\left( {{x_0},{y_0}} \right)$ 即无人机中点坐标位置。应用该方法可有效检测无人机坐标，误差范围小，检测精确，可排除噪点干扰^[7]。其效果如图5所示。可以看出，检测计算中心点与无人机实际中心点基本重合。

3 系统实验测试

采用大疆M100开发者套件作为目标无人机进行实验测试，其搭载的可扩展飞行平台，可实现外部设备接入，开发方便，稳定性高，为测试提供了稳定的检测目标。摄像头采用罗技C270摄像头，罗技Fluid Crystal技术算法可以自动调节帧率、颜色和清晰度等，从而使得拍摄的画面更加清晰。此外，RightLight技术可以自动适应光线，使其可以适应户外多变的天气条件，为图像可靠采集提供便利。

针对该方法做了不同情况下的实验，测试了其在不同干扰下识别无人机的可靠性。经实验可知，本文方法可行有效，识别无人机准确可靠，能有效排除杂物干扰，且对天气有一定的适应性。

由图6可知，图像中云的分布不均匀，且有大块灰色区域，然而背景差方法依然能够准确地提取无人机，且能准确识别。说明该方法对天气情况有一定的适应性，可以保证复杂天气情况下任务的顺利执行。

由图7可知，存在杂物、噪点干扰情况下，图像中存在若干大小不一的噪点以及与无人机大小相似的杂物，虽然背景差无法去除该噪点和杂物，但是霍夫直线变换依然不受其影响，有效、准确地识别出了无人机中心位置。说明该方法对噪点及杂物干扰有较强的适应性，可有效排除噪点干扰，可在大风、脏乱的地方执行无人机降落任务，且准确识别无人机。

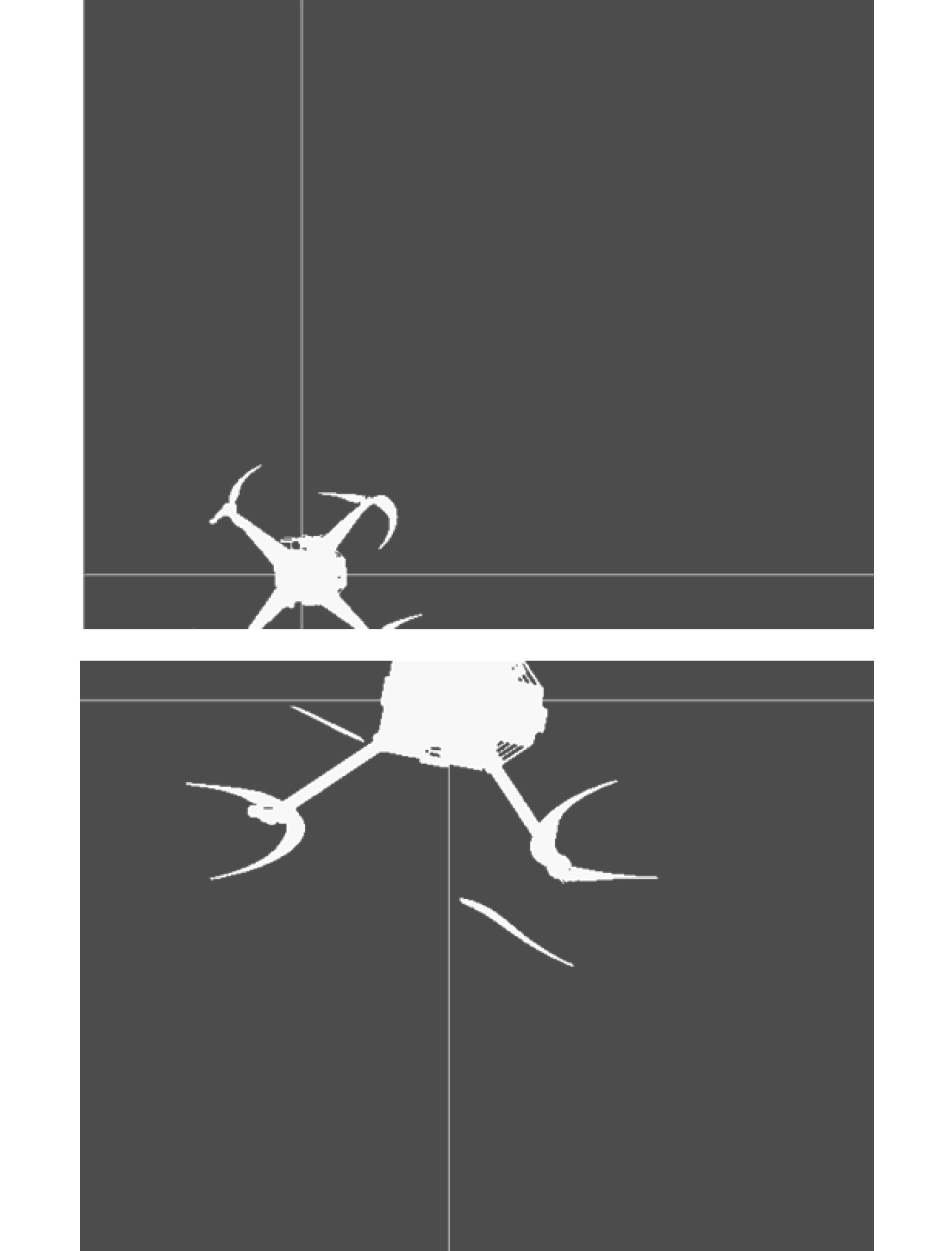
由图8可知，在无人机残缺情况下，该方法依然可以准确识别无人机中心点方位。说明该方法可以在无人机刚进入视野中时便锁定无人机，并对无人机进行实时锁定，保证无人机降落准确。

4 结　语

针对舰载无人机精准降落技术—无人机识别定位问题进行研究，提出基于图像处理的地面站摄像头定位法，采用摄像头拍摄无人机并识别的方法定位无人机，然后通过无人机相对于图像中点的方法进行位置调节，达到无人机精准降落的目的。由于使用了静态背景图像，在极端恶劣天气下可能因为天气变化太大、乌云运动等因素妨碍无人机与背景的分离，导致不能有效识别无人机，从而无法对无人机进行有效引导。需要在后续工作中引入动态背景算法，以提高该方法的适应性，提高无人机精准降落的可靠性。