2. 中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;
3. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169
2. State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China;
3. Institutes for Robotics and Intelligent Manufacturing Innovation, Chinese Academy of Sciences, Shenyang 110169, China
自主式水下机器人(Autonomous Underwater Vehicle, AUV)是一种综合了多种船舶、机械、推进、计算机等先进技术的自主式无人潜器。近年来,因全球对海洋探测要求的不断提高,AUV被应用于水文观测、海洋监测、地质和生物调查等领域[1]。但是由于AUV在水下作业中需要消耗大量能源且自身所能携带的能源有限,AUV每次能源耗尽前必须返回水面工作台进行能源补充,这极大限制了AUV的海洋环境探测能力,并消耗了大量人力、物力[2]。经过近几年相关领域的探索和研究,发现可以通过在水下建立对接DOCK的方法解决此类问题[3-5]。
现阶段,国内外学者对AUV对接进行了一系列相关研究,赵国良等[6]研究了喇叭口式对接系统喇叭口剖面半径与初始中心线偏移量对接驳过程的影响;Tao等[7]通过多体动力学分析软件对刚度系数、阻尼系数、初始速度、偏移角等因素单独进行研究,得到了以上因素对AUV接驳过程中碰撞力的影响。Meng等[8]通过流体动力学仿真软件,研究了与捕捉杆式对接系统在捕获时与碰撞力有关的影响因素。Cheng等[9]研究了双体之间水动力的相互作用,得到了2个物体在不同间隙比、不同雷诺数、不同迎角、不同表面形状下的相互作用力。但是目前还没有对DOCK对接时进行水下综合特性分析的研究,尤其是没有通过双向流固耦合分析其特性研究,因此对DOCK对接时进行整体机构的精确特性分析具有一定意义。
AUV和DOCK在水下的对接过程是一个极其复杂的过程,这个过程既要考虑DOCK的变形情况对水流的扰流动影响,又要考虑水流流动对发生形变后DOCK的冲击影响,因此可以采用双向流固耦合的方法模拟外界条件,双向流固耦合可以通过系统动网格重构展示数字模型的变形情况。同时为了得到准确的瞬态结构场数据,采用接触碰撞法利用多体动力学软件对AUV与DOCK的对接过程进行虚拟仿真,确定碰撞载荷的大小。本文研究可为AUV水下对接操作提供技术支持,对水下对接的相关研究具有一定的参考价值。
1 相关设计模型 1.1 DOCK的数字模型常见的对接装置可以分为捕捉杆式对接系统、飞机坐落式对接系统和锥形罩式对接系统,现阶段研究最广泛的对接装置依然是基于喇叭口状的锥形导向罩DOCK对接系统[10]。该类装置通常使用渐缩型的入口装置进行导向,使AUV进入预定的轨道完成对接。典型的锥形罩式对接系统有美国研发的REMUS AUV水下对接系统、哈尔滨工程大学研制的“海灵”号水下对接装置以及中国科学院沈阳自动化研究所、浙江大学、日本东京大学等相关机构研究的项目[11]。根据对以上锥形罩式对接装置的研究,本文设计并改进了一种新型锥形罩式DOCK,该DOCK可以通过锥形罩对AUV进行导向,通过对接爪与AUV进行对接,通过齿轮齿条对中机构对AUV进行固定,保证AUV的各个自由度都可以被限制,其新型DOCK的数组模型如图1所示。

|
图 1 新型DOCK的数字模型 Fig. 1 A digital model of the new DOCK |
通常来讲,接触可以分为法向接触和切向接触2种。法向接触是面对面的直接接触,其中又分为例如冲压的持续接触和例如碰撞的瞬时接触,而切向接触通常伴随着摩擦接触。AUV与DOCK的碰撞属于一种既包含瞬时碰撞的法向接触,又包含库伦摩擦的切向接触的综合接触。对于这种复杂接触,可以采用等效弹簧阻尼法分析AUV与DOCK发生对接碰撞时的碰撞参数,其碰撞恢复系数为:
| $ {{e = }}\frac{{{v_2} - {v_1}}}{{{v_{10}} - {v_{20}}}}。$ | (1) |
式中:
假设AUV接触曲率半径为
| $ F = k{\delta ^z} + D\dot \delta 。$ | (2) |
其中:
| $ D = \lambda {\delta ^{\text{z}}} ,$ | (3) |
| $ k = \frac{4}{{3{\text{π}} ({\sigma _1} + {\sigma _2})}}\Bigg(\frac{{{r_1}{r_2}}}{{{r_1} + {r_2}}}\Bigg)^{1/2} ,$ | (4) |
| $ {\sigma _i} = \frac{{1 - {v_i}^2}}{{{\text{π}} {E_i}}} 。$ | (5) |
式中:
流固耦合指流体与固体之间的相互作用。流固耦合的基本方程为:
| $ {{\boldsymbol{M}}^\prime }{\ddot{{X}}}_{{d}} + {{{{\boldsymbol{C}}}}^\prime }{ \ddot{{x}}_{{d}}} + {{\boldsymbol{K}}^\prime }{{{x}}_{{d}}} = {{{F}}_{{d}}}。$ | (6) |
式中:
| $ {{\boldsymbol{M}}^\prime } = \left| {\begin{array}{*{20}{c}} {\boldsymbol{M}}&0 \\ {{{\boldsymbol{M}}^{{{fs}}}}}&{{{\boldsymbol{M}}^{{q}}}} \end{array}} \right| ,$ | (7) |
| $ {{\boldsymbol{C}}^\prime } = \left| {\begin{array}{*{20}{c}} {\boldsymbol{C}}&0 \\ 0&{{{\boldsymbol{C}}^{{q}}}} \end{array}} \right|,$ | (8) |
| $ {{\boldsymbol{K}}^\prime } = \left| {\begin{array}{*{20}{c}} {\boldsymbol{K}}&{{{\boldsymbol{K}}^{{{fs}}}}} \\ 0&{{{\boldsymbol{K}}^{{q}}}} \end{array}} \right|,$ | (9) |
| $ {\stackrel{\mathrm{..}}{{X}}}_{{d}}=\left\{\begin{array}{c}\stackrel{\mathrm{..}}{{x}}\\ \stackrel{\mathrm{..}}{{q}}\end{array}\right\},{\dot{{x}}}_{{d}}=\left\{\begin{array}{c}\stackrel{.}{{x}}\\ \stackrel{.}{{q}}\end{array}\right\},{{x}}_{{d}}=\left\{\begin{array}{l}{x} \\ {q} \end{array}\right\},{{F}}_{{d}}=\left\{\begin{array}{c}{F}\\ 0\end{array}\right\} 。$ | (10) |
式中:
虽然普通流固耦合可以满足大部分耦合要求,但是有些对于精度要求较高的耦合系统中,即需要考虑流体对物体产生的影响,又要考虑物体对流体产生的影响,这种考虑综合影响的耦合称作“双向”耦合,双向耦合将计算域分为流体域和瞬态结构域,并通过系统耦合连续地传递作用力,其中流固耦合界面满足的动力条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {{d_f} = {d_s}},\\ {n \cdot {\tau _f} = n \cdot {\tau _s}} 。\end{array}} \right. $ | (11) |
式中:
常见的双向耦合方法分为直接耦合法和分离法,本文应用的是直接耦合法,直接将流体和固体的控制方程联立在一个矩阵中进行求解,计算原理为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{A}}_{ff}}}&{{{\boldsymbol{A}}_{fs}}} \\ {{{\boldsymbol{A}}_{sf}}}&{{{\boldsymbol{A}}_{ss}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\Delta }}{\boldsymbol{X}}_f^k} \\ {{{\Delta }}{\boldsymbol{X}}_s^k} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_f}} \\ {{B_s}} \end{array}} \right] 。$ | (12) |
式中:
ADAMS是MSC公司开发的多体动力学的虚拟样机仿真软件,是目前最权威的机械系统动力学仿真软件,被广泛应用于虚拟样机测试中,因此选择ADAMS软件进行模拟。
2.1.1 参数选取采用IMPACT冲击函数模型对AUV的对接进行研究,IMPACT定义碰撞的广义函数为[13]:
| $ {F_n} = k{\delta ^c} + Cv。$ | (13) |
式中:
接触刚度的Hertz理论计算[14]公式为:
| $ k = \frac{4}{{3{\text{π}} ({\sigma _1} + {\sigma _2})}}{(\frac{{{r_1}{r_2}}}{{{r_1} + {r_2}}})^{1/2}} 。$ | (14) |
式中:
阻尼系数根据Lankarani等提出的修正迟滞阻尼系数计算式为:
| $ C = \frac{{3k(1 - {e^2})}}{{4u}}{\delta ^n} 。$ | (15) |
式中:
力指数和材料的非线性程度有关,通常用来计算瞬时法向力中材料刚度项贡献值,根据ADAMS软件的官方帮助文件可知,该数的范围在1~3内。对于金属材料,力指数通常可以取1.3~1.5,而对于橡胶材料,力指数通常可以取到2~3。
渗透量为全阻尼时的穿透值,穿越值为0时,阻尼系数为0。在ADAMS软件中,可以运用三次STEP函数求解阻尼系数。渗透量与刚度成反相关,与力指数成正相关,该值仍然选自帮助文档。
另外还需注意的是,接触碰撞还要考虑切向接触,切向接触中即需要考虑静摩擦系数
根据研究及其已知条件,可以确定仿真的所有参数,如表1所示。
|
|
表 1 仿真确定的参数 Tab.1 Parameters determined by simulation |
将DOCK进行简化,去除不必要的对接爪、齿轮齿条对中机构等部件,使之仅保留DOCK的骨架。通过对AUV施加初速度、牵引力约束,对DOCK施加固定约束,对AUV和DOCK施加碰撞约束,并测量碰撞力。在ADAMS中设置约束,如图2所示。

|
图 2 对接系统的虚拟样机模型 Fig. 2 Virtual prototype model of docking system |
为了使仿真效果更接近真实情况,在初始状态中,将AUV与DOCK错开一定距离,使AUV接触DOCK后,由锥形导向罩进行引导对接。运行虚拟样机,并通过ADAMS自带的测量工具进行测量,得到的数据如图3所示。可以看出AUV存在多次碰撞,最终AUV顺利抵达DOCK末端完成对接,其中第一次碰撞是AUV与DOCK的锥形导向罩的对接,接下来是AUV与DOCK中间肋板的碰撞,最后一次是AUV与DOCK末端的对接,本文研究的对象为AUV与DOCK完成对接时的最后一次碰撞,故选择此参数作为瞬态结构场的外力约束。
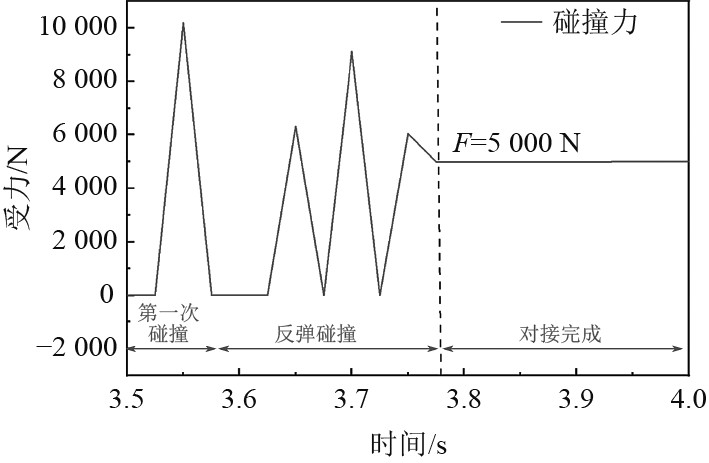
|
图 3 虚拟样机测得的碰撞数据 Fig. 3 Collision data measured by virtual prototype |
将得出的瞬态结构场条件设置在有限元软件中,并通过系统耦合耦合到流场中,通过系统耦合的物理场,可以同时处理AUV的碰撞力对水流的扰流动影响和水流流动对碰撞力的影响。仿真软件选择Ansys Workbench,相对其他CAE有限元分析软件,其特点功能全面,可通过工作台将模块进行耦合分析。
2.2.1 瞬态结构场的设置使用四面体网格划分DOCK框架,同时将结构复杂的面上进行加密,最终划分为8187个单元,网格划分情况如图4所示。通过网格质量检测可以看到网格平均质量大于0.7,因此网格划分质量较好。

|
图 4 DOCK结构场的网格划分 Fig. 4 Meshing of DOCK structure field |
根据DOCK实际情况,设置各处约束。将DOCK末端设置一个接触面为圆的形冲击力,代表AUV的最后一次碰撞力,输入测试得到的结果;将DOCK框架的底部设置为固定约束;将DOCK整个框架设置为流固交涉面,表示整体结构同时受到流场和结构场的影响,并将整体变形、等效应力和等效应变设为待求解。最终,DOCK的状态如图5所示。

|
图 5 DOCK结构场的约束情况 Fig. 5 DOCK structure field constraints |
由于需要考虑外流场的作用,在流场分析中需要给DOCK添加外流域。在流场建模中,给DOCK外侧添加一个六面体作为外流场。同时,划分网格时,除瞬态结构场的操作外,还需划分外流域网格,并在DOCK表面添加棱柱层网格,最终得到65036个网格,网格划分情况如图6所示。平均网格质量大约为0.85,因此整体网格划分质量较好,将各个面命名后完成预处理。

|
图 6 DOCK流体场的网格划分 Fig. 6 Meshing of DOCK fluid field field |
选择多核并行处理器,进行3D模型流体求解。选择类应为基于压力,时间为瞬态,选择标准
为了有更好的观看效果,分别将xz平面和yz平面显示出来,并保留DOCK框架,隐藏外流域模型,DOCK的最终状态如图7所示。
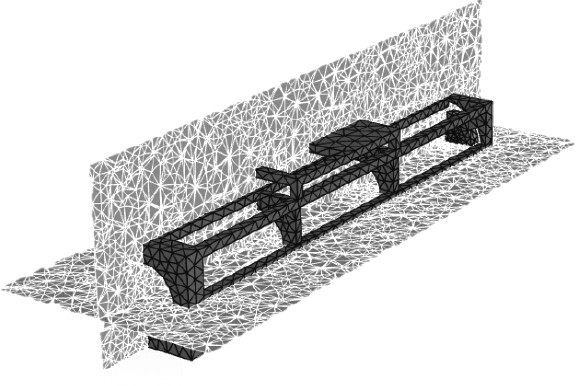
|
图 7 DOCK流体场的约束情况 Fig. 7 DOCK fluid field field constraints |
建立系统耦合模块,设置数据传输信息,将流场的表面应力添加到瞬态结构场的表面应力;将瞬态结构场的位移形变添加到流场的位移形变中,进行耦合求解。由求解收敛图可以看出耦合效果较好,每个时间步的耦合系数都已收敛,经过求解后,可以得到DOCK的等效变形图、等效应力图、等效应变图和流场压力图。
图8为DOCK承受的等效变形图、等效应力图、等效应变图。由图8(a)可知,整个DOCK中,变形最大处为上支撑台,数值为7.0069E-5 m;变形最小处为DOCK底面,数值为0 m,其中整体趋势为由下到上变形依次增大,这是由于DOCK的底面为固定面导致的。由图8(b)可知,整个DOCK中,变形最大处为DOCK尾部与下平面的连接处,数值为8.1036E-6 m/m;变形最小处为DOCK底面,数值为1.997E-9 m/m,其中整体趋势为框架连接处较大,这是由各个框架的疲劳寿命系数决定的。由图8(c)可知,变形最大处为DOCK尾部与下平面的连接处,数值为1.4688E-6 Pa;变形最小处为DOCK底面,数值为98.5 Pa,其中整体趋势也为框架连接处较大,这也是由各个框架的疲劳寿命系数决定的。因此应加固DOCK框架连接处以及上方结构。
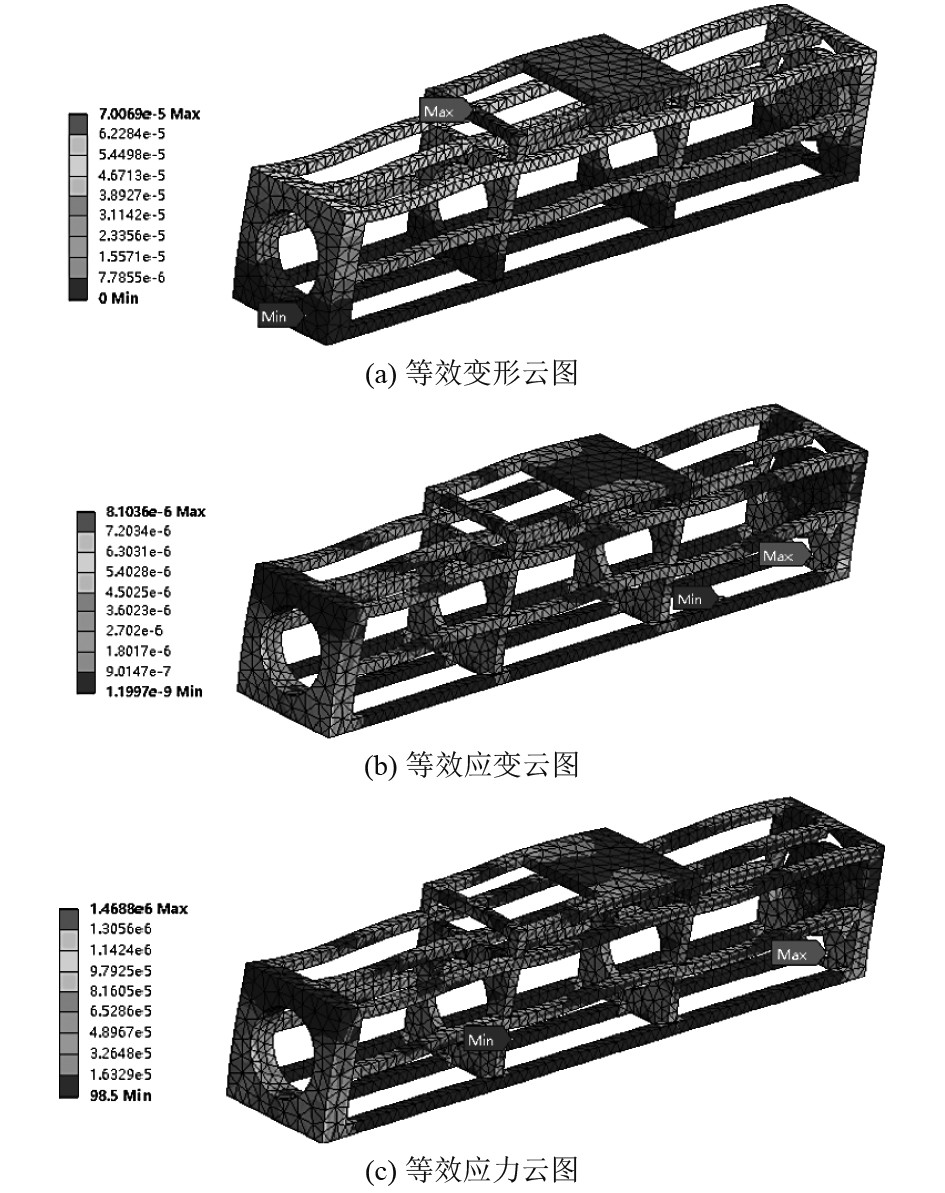
|
图 8 DOCK应力、应变、变形结果云图 Fig. 8 DOCK stress, strain, deformation results cloud diagram |
图9为DOCK的内外流场压力云图,其中迎流面压力最大,最大值为4.88E5 Pa,剩余的迎流面压力依次逐渐减小,周围压力比较稳定,基本保持在2.44E5 Pa左右。开始时头部压力较大,之后随着流场稳定压力逐渐低并稳定。因此,应对每个迎流面进行加固,尤其是第一个面。

|
图 9 DOCK流体压力云图 Fig. 9 DOCK fluid pressure cloud diagram |
本文以设计的一款新型锥形罩式DOCK为研究对象,对DOCK对接结果特性进行相对精确的分析,结论如下:
1)通过系统虚拟样机仿真得到了AUV对接过程的瞬态运动及其受力情况,并施加到有限元仿真的结构场中进行流固耦合分析。仅通过基本数据就实现了对对接过程DOCK状态的综合分析。
2)通过对双向流固耦合的变形云图分析可以发现,DOCK的变形趋势为由上到下逐渐减少,且上方的变形远远大于下方,因此DOCK上方需要添加更强鲁棒性的材料,以保证DOCK的稳定性,其材料可以根具变形云图中的具体数值进行合理的搭配。
3)通过对双向流固耦合的应变和应力云图分析可以发现,支撑杆和一些垂直板处应力应变较大,且应力应变最大处和最小处分别位于DOCK的框架及平面的连接处和DOCK底座处,因此要着重对此连接处进行加固,其加固情况可以根具应应力变云图中的具体数值进行相应的修正。
4)通过对双向流固耦合的内外流场云图分析可以发现,DOCK的迎流面附近的外流场和表面压强较大,数值大约比系统平均压强高1倍,比后方的迎流面压强高1/3倍,同时迎流面接触面积较大的地方压强也有明显的提升,针对受到水压较大的地方可以根据云图结果的具体数值进行适当的调节。
5)在实际工程中,还可以根据实际需求在Workbench中添加其他需求解结果,本文所述的方法均可实现求解。
| [1] |
KRONEN D M, UNIVERSITY F A. Docking the ocean explorer autonomous underwater vehicle using a low-cost acoustic positioning system and a fuzzy logic guidance algorithm[M]. Florida Atlantic University, 1997.
|
| [2] |
DAVIS D T. Precision control and maneuvering of the phoenix autonomous underwater vehicle for entering a recovery tube[J]. Monterey, California: Naval Postgraduate School, 1997.
|
| [3] |
郑荣, 宋涛, 孙庆刚, 等. 自主式水下机器人水下对接技术综述[J]. 中国舰船研究, 2018, 13(6): 43-49+65. ZHENG R, SONG T, SUN Q, et al. Review on underwater docking technology of autonomous underwater vehicle[J]. Chinese Ship Research, 2018, 13(6): 43-49+65. DOI:10.19693/j.issn.1673-3185.01182 |
| [4] |
SINGH H, BELLINGHAM J G, HOVER F, et al. Docking for an autonomous ocean sampling network[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 498-514. DOI:10.1109/48.972084 |
| [5] |
燕奎臣, 吴利红. AUV水下对接关键技术研究[J]. 机器人, 2007(3): 267-273. YAN K C, WU L H. Research on key technology of AUV underwater docking[J]. Robot, 2007(3): 267-273. DOI:10.3321/j.issn:1002-0446.2007.03.014 |
| [6] |
赵国良, 许可, 赵春城, 等. 导向喇叭口剖面半径对AUV回收的影响[J]. 水下无人系统学报, 2018, 26(2): 166-173. ZHAO G L, XU K, ZHAO C C, et al. Influence of guide bell profile radius on AUV recovery[J]. Journal of Underwater Unmanned Systems, 2018, 26(2): 166-173. |
| [7] |
TAO Z, LI D, YANG C. Study on impact process of AUV underwater docking with a cone-shaped dock [J]. Ocean Engineering, 2017, 130: 176–187.
|
| [8] |
MENG L, LIN Y, GU H, et al. Study on dynamic docking process and collision problems of captured-rod docking method [J]. Ocean Engineering, 2019, 193: 106624–106631.
|
| [9] |
CHENG L. Hydrodynamic interactions between two bodies [J]. Journal of Hydrodynamics, 2007, 19: 784–785.
|
| [10] |
KAWASAKI T, FUKASAWA T, NOGUCHI T, et al. Development of AUV marine bird with underwater docking and recharging system[C]//International Workshop on Scientific Use of Submarine Cables & Related Technologies. IEEE Xplore, 2003.
|
| [11] |
WU L, LI Y, SU S, et al. Hydrodynamic analysis of AUV underwater docking with a cone-shaped dock under ocean currents[J]. Ocean Engineering, 2014, 85(15): 110-126. |
| [12] |
LANKARANI H M, NIKRAVESH P E. A contact force model with hysteresis damping for impact analysis of multibody systems[J]. Journal of Mechanical Design, 1990, 112(3): 369-376. DOI:10.1115/1.2912617 |
| [13] |
LANKARANI H M, NIKRAVESH P E. Continuous contact force models for impact analysis in multibody systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207. DOI:10.1007/BF00045676 |
| [14] |
史剑光, 李德骏, 杨灿军, 等. 水下自主机器人接驳碰撞过程分析[J]. 浙江大学学报:工学版, 2015, 49(3): 497-504. SHI J G, LI D J, YANG C J, et al. Analysis on collision process of underwater autonomous robot[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(3): 497-504. |
 2023, Vol. 45
2023, Vol. 45
