2. 北京航空航天大学 机械工程及自动化学院, 北京 100191
2. School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China
随着人类社会的进步与发展,陆地的资源和矿产不断被开发与消耗,各国逐渐将发展的目光投向占地球表面积70%的海洋。深海潜水器是实现海洋开发利用的重要海洋工程装备[1]。根据作业使命任务的不同,各国先后研制出了不同类型的深海潜水器,主要包括载人潜水器(HOV)、缆控无人潜水器(ROV)、无缆自治式无人潜水器(AUV)[2],除螺旋桨推进方式外,近几年又出现了一种新的无人无缆多腿爬行式深海潜水器[3]。
深海爬游混合型无人潜水器(以下简称爬游潜器)是十三五重点研发计划项目,是一种既可在深海巡游,又可海底爬行的爬游混合型无人无缆潜水器。甲板操控单元通过USBL通信系统,向深海作业的爬游潜器发送控制指令并接收其状态信息,以此实现对其在水底和水中的作业控制,并掌握其状态和轨迹信息。为实现对爬游潜器有效安全的操控,首先必须获取稳定可靠的定位信息,对水下轨迹进行预测。
1 爬游潜器水下定位海试方案无人潜航器(UUV)在海中和海底采用的常用定位手段有惯性原理、重力场匹配、地磁辅助、声觉、视觉、地形辅助等[4-6]。爬游潜器水下定位采用水声定位方式,配备水声通信系统是Evologics的USBL,标称垂向通信锥角为120°,适用于深海垂向大深度的水声通信,因此契合深海爬游混合的应用场景。通过超短基线系统实现对爬游潜器定向和定位。超短基线定位系统确定水下目标位置是通过测量信号的到达方位和距离实现,测向任务是通过测量信号到达接收基阵基元之间的相位差实现的,它是超短基线定位系统的关键。一般来说,最少需要3个接收基元构成平面接收阵才能够作为短基线阵进行目标的三维定位[7]。
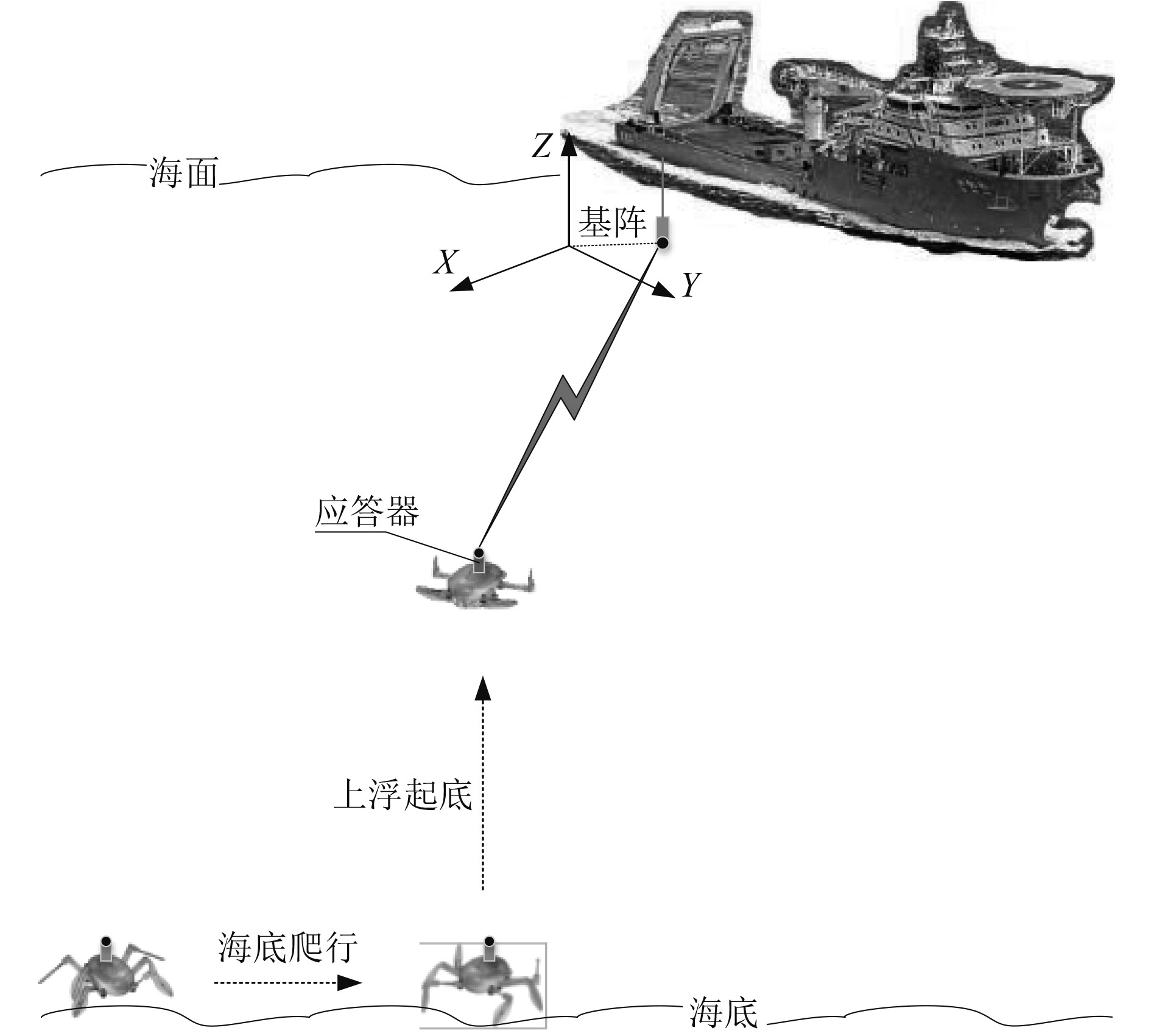
爬游潜器搭载在“深潜”号上,开展演示验证试验。超短基线应答器部署在爬游潜器背部,而超短基线基阵通过刚性连接,部署在“深潜”号右舷,离开母船螺旋桨一定距离,且低于船底最低处2~3 m,降低环境影响,获取更优的水声通信环境。图1为爬游潜器深海海试过程中USBL系统的实际安装配置方式。
|
图 1 爬游潜器海试定位方案 Fig. 1 Locating scheme of craw-swimming vehicle (CSV) sea trial |
爬游潜器从“深潜”号右舷吊入水中,脱扣后开始下潜,到达一定深度后进入USBL通信锥角内,建立水声通信连接。通信连接一旦建立,USBL基阵依据通信建立过程中,声波发送和接收的间隔计算爬游潜器的定位信息,并发送给爬游潜器的甲板操控单元进行显示和存储。下潜定位数据(截取部分)如表1所示。通过分析,可得下述结论:1)异常值在定位过程中随机出现,如表第2、5、8行所示;2)基阵建立定位,向甲板操控单元上发定位数据时间间隔不一致,如时间列所示。
|
|
表 1 爬游潜器下潜过程USBL定位数据(截取部分) Tab.1 CSV USBL locating data of diving (fragmented) |
异常值的随机出现使得无法直接采用USBL数据进行爬游潜器的定位显示,时间间隔不一致的问题会导致无法直接应用常用滤波算法。
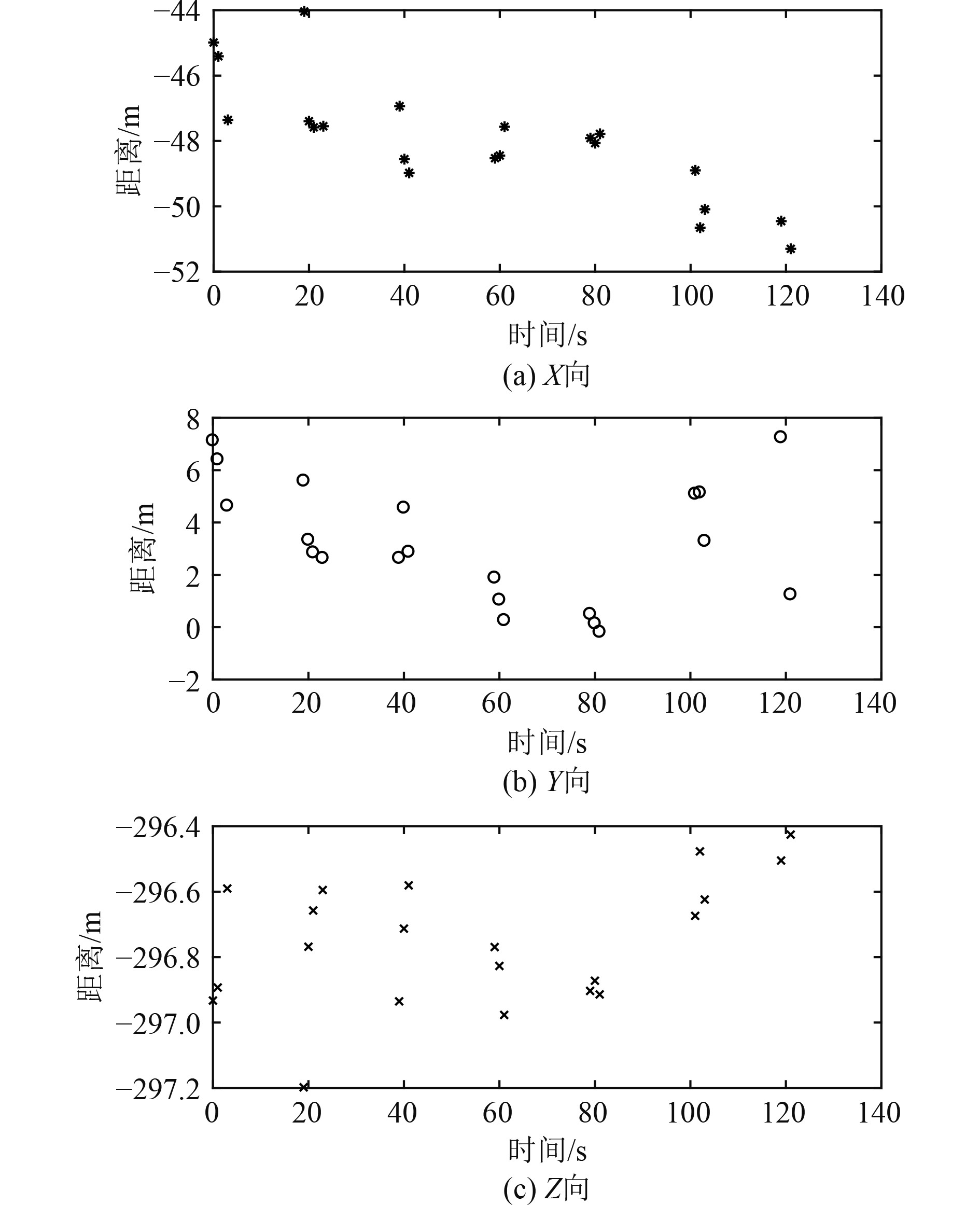
2.2 对爬游潜器在海底驻留过程数据分析在爬游潜器单一完整潜次中,母船“深潜”号动力定位开启,左舷挡风挡流,尽量降低爬游潜器海试过程中的定位受环境和试验条件的影响。爬游潜器顺利坐底后,在甲板单元未主动下达运动指令时,其在海底的绝对位置不发生变化,分析此间140 s时间内母船与爬游潜器的相对定位数据,其相对位置均值及方差如表2所示,爬游潜器x向、y向、z向位置随时间的分布如图2所示。即使母船有先进的动力定位,但是浪和涌引起母船微弱的升沉和摇摆影响了USBL基阵和应答器的方位和距离,同时耦合了水声测量的误差,进而影响了定位的准确性和一致性,产生系统误差。
|
|
表 2 爬游潜器坐底USBL定位数据数值特征 Tab.2 CSV USBL statistic value of locating data motionless at bottom |
|
图 2 爬游潜器坐底USBL定位数据 Fig. 2 CSV USBL locating data of motionless at bottom |
USBL系统基阵与应答器之间存在通信锥角,不同厂商和型号均不同,一般锥角在60°~180°,锥角与基阵阵列的布置有关。当潜航器与母船的相对位置超出USBL通信锥角时,母船的USBL基阵和爬游潜器的应答器之间无法建立水声通信,因此母船无法确切得到潜器的位置与出水点,存在潜航器与船体碰撞或者潜航器在母船底部或附近出水,被吸入母船螺旋桨的安全风险。
2.4 USBL定位数据直接使用存在的问题总结通过上述对试验数据和USBL自身特性的分析,直接使用USBL的定位数据来确定爬游潜器的水下轨迹和位置存在误差,同时也存在很大的安全风险。因此,提出一种基于USBL定位数据的递归最小二乘法轨迹预测算法[2]。
3 基于USBL定位数据的轨迹预测算法 3.1 算法概述针对USBL数据直接定位存在问题,提出如下爬游潜器的轨迹预测算法:
1)数据剔除异常值;
2)按水声通信节拍,对定位时刻进行聚类分析,通过拉格朗日二次多项式插值,将数据按周期对齐;
3)建立量测模型,通过递归最小二乘法对状态量进行最优估计;
4)分段按照各最小二乘法的最优估计值进行多项式展开,对周期间和周期外的定位轨迹进行预测。
3.2 算法具体实施1)数据去异常值
爬游潜器在水下惯性很大,运动变化率小,属于缓慢运动,因此可以设置方位变化率阈值进行定位数据异常值的剔除。
2)按水声通信节拍,对定位数据进行聚类分析,并进行数据按周期对齐
爬游潜器水声通信的周期是20 s,通信前基阵和应答器需建立水声通信链路,定位信息是在通信链路建立的握手过程和数据通过水声通信链路收发过程中建立。从定位时刻分布看连续数次定位由单次水声通信过程产生,如定位时刻表3所示。
|
|
表 3 爬游潜器坐底USBL定位时刻表 Tab.3 USBL locating instant when CSV motionless at bottom |
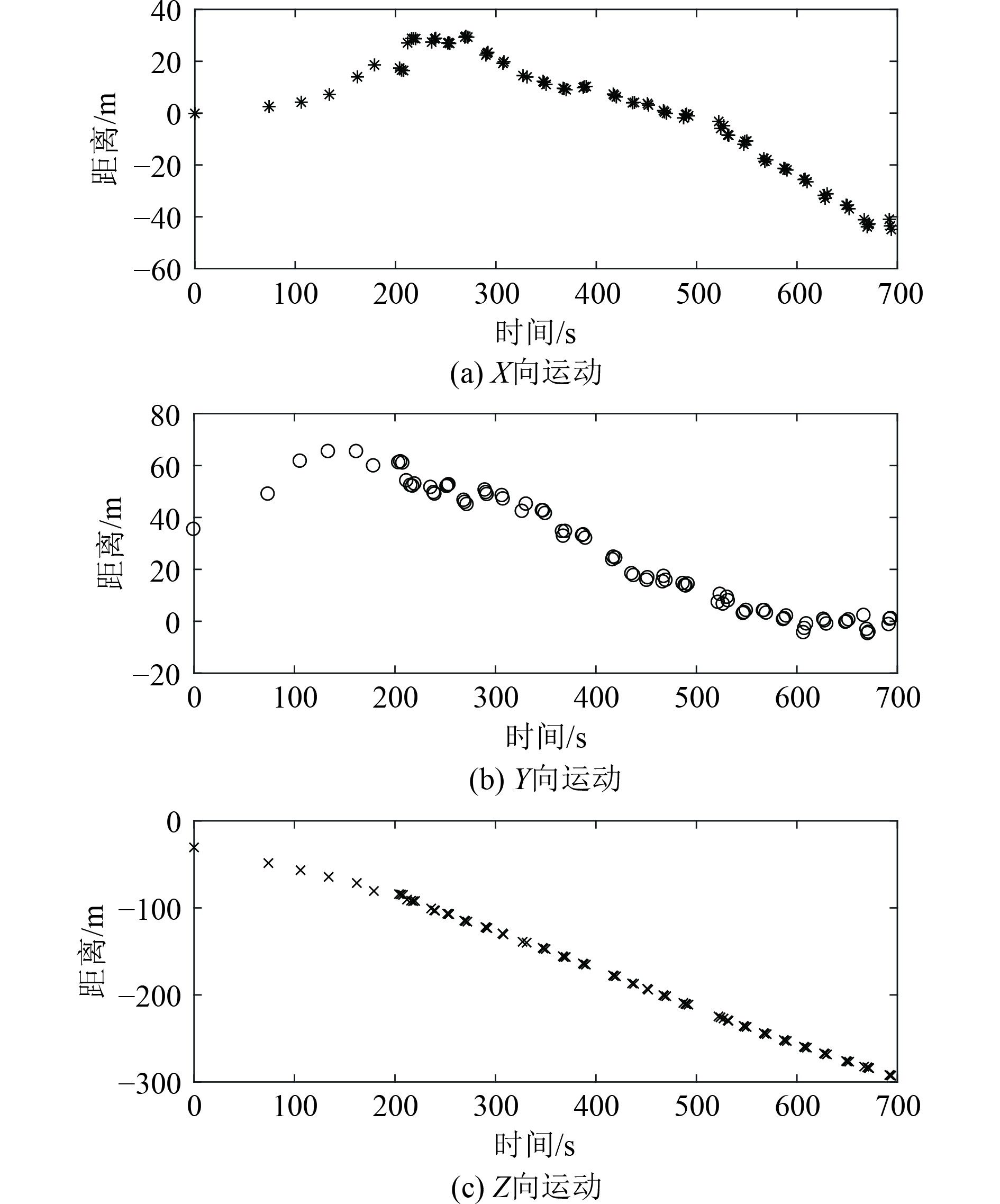
爬游潜器下潜过程中的USBL定位数据如图3所示(异常值已经剔除)。可以看出,在下潜全过程中,水深较浅时,水声通信建立比较差,定位次数也比较少;水深增大时,单次水声通信都可完成多次水声并将定位信息上传至上位机。但也发现,定位信息相对节拍点时刻并不完全对中,为能进行最优估计,定位数据需按周期给出。
|
图 3 爬游潜器下潜过程USBL定位数据 Fig. 3 USBL locating data when CSV is diving |
因此对USBL定位数据进行实时聚类[8],分析单次水声通信的定位值,选用拉格朗日插值法,对数据按时间进行周期对齐,方法如下:取聚类分析后连续3个时刻,使用拉格朗日二阶多项式插值公式(1)进行插值运算[9]。
| $ \left\{ \begin{gathered} {l_1}(t) = \frac{{(t - {t_2})(t - {t_3})}}{{({t_1} - {t_2})({t_1} - {t_3})}},\\ {l_2}(t) = \frac{{(t - {t_1})(t - {t_3})}}{{({t_2} - {t_1})({t_2} - {t_3})}},\\ {l_3}(t) = \frac{{(t - {t_1})(t - {t_2})}}{{({t_3} - {t_1})({t_3} - {t_2})}},\\ {L_2}(t) = {l_1}(t)f({t_1}) + {l_2}(t)f({t_2}) + {l_3}(t)f({t_3})。\\ \end{gathered} \right. $ | (1) |
式中:(t1, f(t1))、(t2, f(t2))、(t3, f(t3))为聚类分析后的3个已知点;l1(t)、l2(t)、l3(t)为二次拉格朗日插值的基函数;L2(t)为二次拉格朗日插值函数。
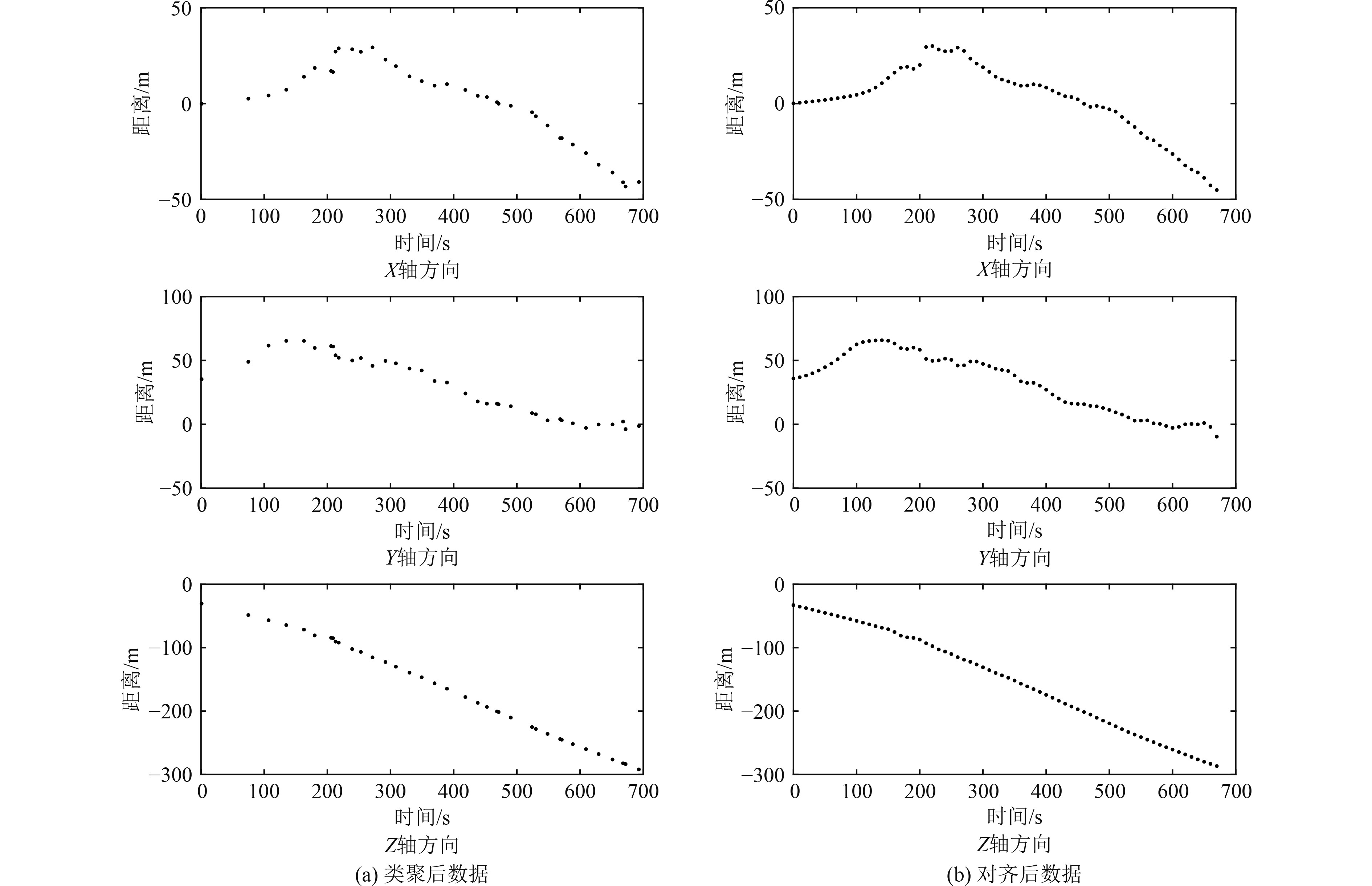
聚类和对齐后数据如图4所示。聚类后属于同一次水声通信产生的多次定位数据进行算术平均,融合为一个点,聚类后数据分布不均匀,如图4(a)所示。采用聚类后的数据进行拉格朗日二次插值,对分段插值函数按周期点取函数值,结果如图4(b)所示。
|
图 4 聚类后数据和对齐后数据 Fig. 4 Data after clustering and alligning |
USBL定位有效数据从水深30 m开始,在这个水深潜航器受水面波浪影响较小,海流是爬游潜器下潜过程主要影响因素,它能使水下机器人运动阻力增大,并产生漂流运动,其形式多种多样。其中定海流与潮流为主要影响类型,其流向、流速的变化比较小或呈一定周期性,因此在一个时间点可近似认为爬游潜器下潜过程的海洋流场为无限大稳恒定流场[10]。按照上述假设建立爬游潜器下潜的状态模型,将其下潜运动分解为X向、Y向和Z向。以X向为例,设tk为数据对齐时刻,zk为该时刻的量测值,状态Xk定义为二次曲线的系数[ak bk ck]T,建立量测方程为:
| $ \begin{split} {Z_k} =& {{\boldsymbol{H}}_k}X{}_k + {\nu _k} = \\ & at_k^2 + b{t_k} + c + {v_k} = \\ & [\begin{array}{*{20}{c}} {t_k^2}&{{t_k}}&1 \end{array}]\left[ {\begin{array}{*{20}{c}} {{a_k}} \\ {{b_k}} \\ {{c_k}} \end{array}} \right] + {\nu _k}。\end{split} $ | (2) |
式中:
按照式(3)开展递归最小二乘估计算法[11]的迭代。
| $ \left\{ \begin{aligned} & {{\boldsymbol{P}}_{k + 1}} = {{\boldsymbol{P}}_k} - {{\boldsymbol{P}}_k}{{H}}_{k + 1}^{\rm{T}}{({\boldsymbol{W}}_{k + 1}^{ - 1} + {{{H}}_{k + 1}}{{\boldsymbol{P}}_k}H_{k + 1}^{\rm{T}})^{ - 1}}{{\boldsymbol{H}}_{k + 1}}{{\boldsymbol{P}}_k} ,\\& {{\hat X}_{k + 1}} = {{\hat X}_k} + {{\boldsymbol{P}}_{k + 1}}{\boldsymbol{H}}_{k + 1}^{\rm{T}}{{\boldsymbol{W}}_{k + 1}}({Z_{k + 1}} - {{\boldsymbol{H}}_{k + 1}}{{\hat X}_k})。\\ \end{aligned} \right.$ | (3) |
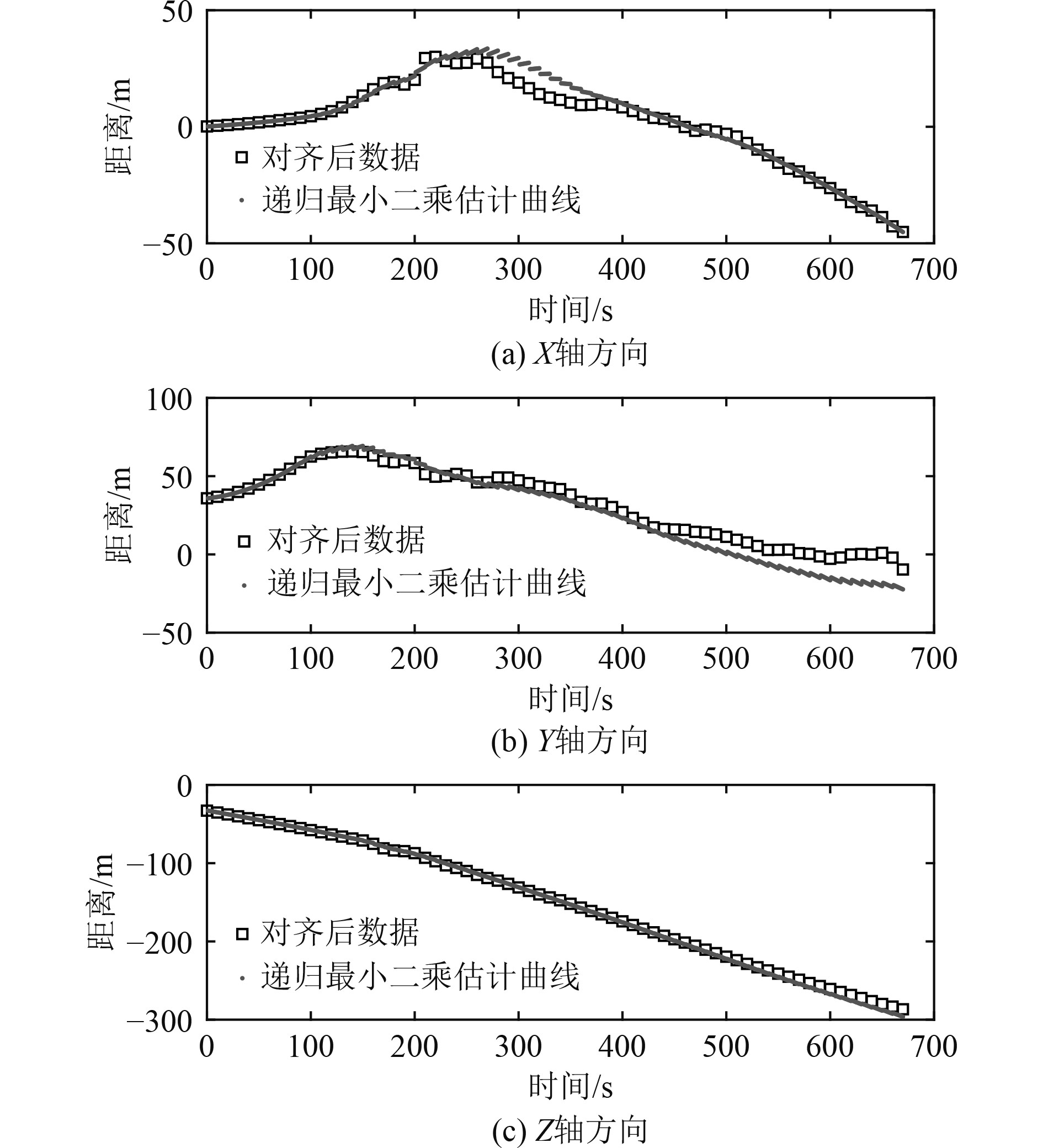
式中:Pk为协方差矩阵;Xk为状态估计;Wk为权重矩阵,取为单位矩阵。初始估计值X0选用USBL最开始3点定位数据的多项式二次拟合的系数,P0选用一个很大的参数作为初始值。完成各周期点的系数状态最小二乘估计后,计算出各个周期点的状态值(即运动二次模型的曲线系数),然后在每个周期内,进行曲线展开。对于节拍之间的时刻和由于USBL水声通信信道不稳定或由于通信锥角导致的通信丢失时的时刻,估计出爬游潜器的下潜的轨迹如图5所示,估计的轨迹图曲率变化连续,相较原始的数据更符合爬游潜器在水中缓慢连续变动的运动特性。
|
图 5 爬游潜器下潜过程最小二乘法估计及分段曲线展开 Fig. 5 RLS result of CSV diving data |
针对使用USBL进行爬游潜器定位和轨迹预测存在的问题,本文提出一种改进型的递归最小二乘法估计的实时处理算法,有效地解决了USBL原始定位数据的数值和时间的随机离散问题,为爬游潜器深海作业的轨迹预测提供解决方案,同时也为其他类型的潜航器的轨迹预测提供借鉴。
| [1] |
封锡盛, 李一平. 海洋机器人 30 年[J]. 科学通报, 2013, 58(增刊II): 2-7 FENG X S, LI Y P. Thirty years evolution of SIA’s unmanned marine vehicles. Chin Sci Bull (Chin Ver), 2013, 58(Suppl. II): 2–7 |
| [2] |
封锡盛, 刘永宽. 自治水下机器人研究开发的现状和趋势[J]. 高技术通讯, 1999, 9(9): 55–59 FENG X S, LIU Y K. Autonomous underwater vehicles development and trend. Chin Sci Bull (Chin Ver), 1999, 9(9): 55–59 |
| [3] |
SEONG-YEOL Y, BONG-Huan J, HYUNGWON S, et al. Design and analysis of carbon fiber reinforced plastic body frame for multi-legged subsea walking robot, crabster[J]. Ocean Engineering, 2015, 102: 78–86.
|
| [4] |
严浙平, 王璐. UUV 水下定位方法的研究现状与进展[J]. 哈尔滨工程大学学报, 2017, 38(7): 989-1000. YAN Zheping, WANG Lu. Research status and progress of UUV underwater localization[J]. Journal of Harbin Engineering University, 2017, 38(7): 989-1000. |
| [5] |
孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015, 34(3): 64-68. SUN D J, ZHENG C E. Study on the development trend of underwater acoustic navigation and positioning technologies[J]. Journal of Ocean Technology, 2015, 34(3): 64-68. |
| [6] |
VICKERY K. Acoustic positioning systems: a practical over- view of current systems[C]//Workshop on Autonomous Underwater Vehicles, 1998, 5–17
|
| [7] |
张同伟, 王向鑫, 唐嘉陵, 等. 深海超短基线定位系统现状及展望[J]. 舰船电子工程, 2018(10): 1-6. ZHANG T W, WANG X X, TANG J L, et al. Technical status and development trend of long range USBL[J]. Ship Electronic Engineering, 2018(10): 1-6. DOI:10.3969/j.issn.1672-9730.2018.01.001 |
| [8] |
JAIN A K. Data clustering: 50 years beyond k-means[C]//19th International Conference on Pattern Recognition, Tampa, USA, 2010: 651–666.
|
| [9] |
关治, 陆金甫. 数值方法[M]. 北京: 清华大学出版社, 2006: 152–161.
|
| [10] |
刘明雍, 张加全, 张立川. 洋流影响下基于运动矢径的 AUV协同定位方法[J]. 控制与决策, 2011, 26(11): 1632-1636. LIU M Y, ZHANG J Q, ZHANG L C. AUV Cooperative localization method based on motion radius vector in the presence of unknown currents[J]. Control and Decision, 2011, 26(11): 1632-1636. |
| [11] |
王可东. Kalman滤波基础及Matlab仿真[M]. 北京: 北京航空航天大学出版社, 2019.
|
 2023, Vol. 45
2023, Vol. 45
