路径规划与避障一直都是水面无人艇研究的重要内容,水面无人艇需具备的自主能力之一是通过感知模块与外界未知环境进行交互获得信息,从而保证水面无人艇能据此进行路径规划和局部避障[1]。基于国内外发展现状以及路径规划与避障技术的重要性,本文针对水面无人艇路径规划与避障领域,运用科学知识图谱的方式对数据进行挖掘,总结技术发展趋势、展望未来研究方向。
1 无人艇感知模块环境感知是无人艇实现路径规划与自主避障的前提。无人艇通过传感器感知环境信息,为后续识别和决策提供支撑[3]。无人艇的传感器大体上可以分为:1)用于外部环境感知,包括激光雷达(Lidar)、单目或双目相机、深度相机、毫米波雷达、红外等,多用于目标识别和跟踪,表1为3种Velodyne激光雷达的性能参数对比,表2为单目相机、双目相机和深度相机三者的优缺点对比;2)用于自身状态感知,包括惯性测量单元(IMU)、GPS等,用于无人艇自身的定位及姿态矫正。
|
|
表 1 Velodyne 激光雷达性能参数对比 Tab.1 Performance parameter comparison of Velodyne Lidar |
|
|
表 2 单目、双目及深度相机对比 Tab.2 Comparison of monocular, binocular and depth cameras |
国内外学者对于感知技术的研究通常集中在外部环境感知方面,如基于可见光成像的目标检测,基于双目或单目视觉的目标跟踪,以及使用激光雷达等测距传感器的水面障碍物定位。通常单一传感器不能全面地反映复杂海况,容易受到天气、距离、自身工作条件等因素的影响[6],出于提高水面目标跟踪与定位的精确度、改善实时检测及跟踪效果差等目的,现阶段环境感知信息的获取不再局限于单个传感器的输入,传感器融合的技术为无人艇感知技术开辟了新道路。David等[7]在2017年提出了一种基于激光雷达和视觉系统融合的海面目标检测跟踪定位方法, Mou等[8]将双目相机同GPS和电子罗盘等进行信息融合,得到了海面障碍物的准确位置。在传感器融合过程中如何克服各个传感器的缺点,提供实时、准确的环境感知信息仍是研究难点,但毫无疑问,多传感器信息融合是未来无人艇环境感知的关键技术[9]。
2 路径规划与避障无人艇的避碰路径规划算法可以分为全局路径规划和局部路径规划两类[10]。
2.1 全局路径规划全局路径规划是依据整个环境构造环境地图后在规定区域内进行的,不能处理规划过程中的突发状况,对实时性要求不高且一般可找到最优解。经典算法有Dijkstra算法、A*算法、蚁群算法、遗传算法等。
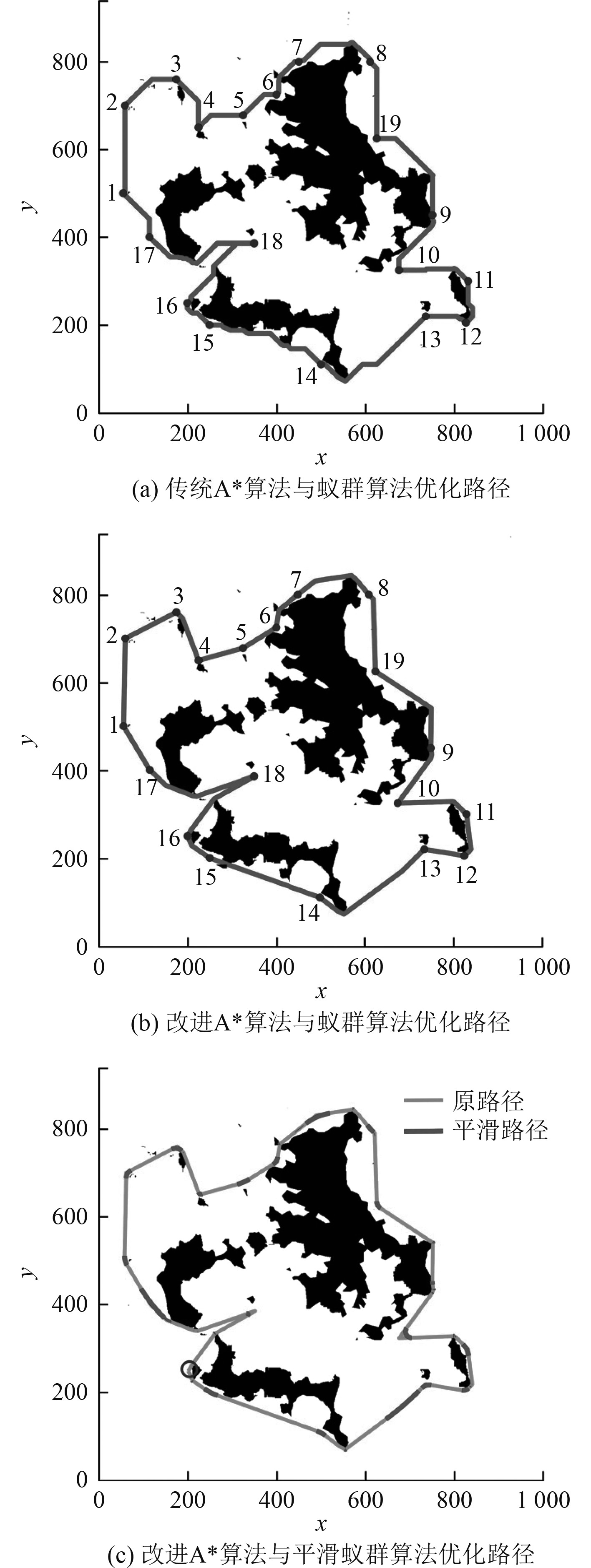
Dijkstra算法[11]是Dijkstra提出的全局规划最短路径算法,该算法虽简单但占用内存大、计算效率低,仅适用于小范围内的路径规划。A*算法[12]是经典的启发式路径规划算法,通过设置代价函数,寻找两点之间的最小代价。由于依赖于启发函数,A*算法计算量巨大,导致规划路径的时间较长。蚁群算法[13]和遗传算法[14]都属于智能仿生学算法,用于处理复杂环境下的路径规划问题。蚁群算法通过迭代模仿蚁群觅食行为寻找最短路径,具有便于并行和鲁棒性强的优点,但设置参数不准确或初期信息素缺少时会出现路径规划速度过慢的问题。张丹红等[15]针对无人艇海上巡逻路径规划问题,提出了A*算法与蚁群算法相结合进行最短巡逻路径优化的方法,效果如图1所示。遗传算法是一种随机化搜索算法,其实质是一种在解空间中搜索与环境最匹配的自适应方法,通过逐步淘汰掉适应性函数低的解,增加适应性函数高的解,从而获得最优路径。遗传算法具有较高的鲁棒性,但其收敛速度较低且控制变量较多,所花费时间要更久。
|
图 1 A*算法与蚁群算法相结合的路径优化效果 Fig. 1 Path optimization effect of A* algorithm combined with ant colony algorithm |
局部避障即局部路径规划是在未知环境下通过传感器获取周围障碍物信息,包括其位置、形状、尺寸等,使无人艇自主生成安全可行的最优路径,其经典算法如人工势场法、动态窗口法、速度障碍法等。
人工势场法最初由Khatib[16]提出,通过建立势场解决实时避障问题,原理简单实时性高,但可能会产生局部最小值的问题。动态窗口法[17]是一种在线避障算法,在窗口不断滚动中实现优化与反馈,准确度较高且计算量小,但算法对航行器的控制要求较高,稳定性较差。汪流江等[18]提出一种基于A*与动态窗口法的混合路径规划算法,在A*算法得到全局路径生成局部目标点后,随着局部目标点的不断更新USV使用动态窗口法航行至全局目标点,图2为该混合路径规划算法与单独采用A*算法的路径搜索结果对比,可以看到混合路径规划对应的路线拐点更少且角度更小。速度障碍法[19]由Fiorini等提出,通过在无人艇与障碍物间的速度空间内构建一个三角区域,当速度向量落入此三角区内判定二者发生碰撞,之后从非三角区域中找到一个最优的速度矢量,实现最优路径避障。速度障碍法考虑动态障碍物的运动信息,算法稳定性高且规划路径准确度高,但速度较慢。

|
图 2 混合路径规划算法仿真结果 Fig. 2 Simulation results of hybrid path planning algorithm |
强化学习(Reinforcement Learning, RL)是机器学习的范式和方法论之一。强化学习的学习机制是智能体通过与环境交互获得对动作的反馈,以“试错”的方式进行学习,目标是使智能体获得最大的奖赏。按照算法的优化机制,强化学习分为基于值函数的方法(Value-based)和基于策略的方法(Policy-based)。前者的代表性算法为深度Q网络(Deep Q Network, DQN)及其改进算法,后者的代表算法有策略梯度算法及其各种形式。
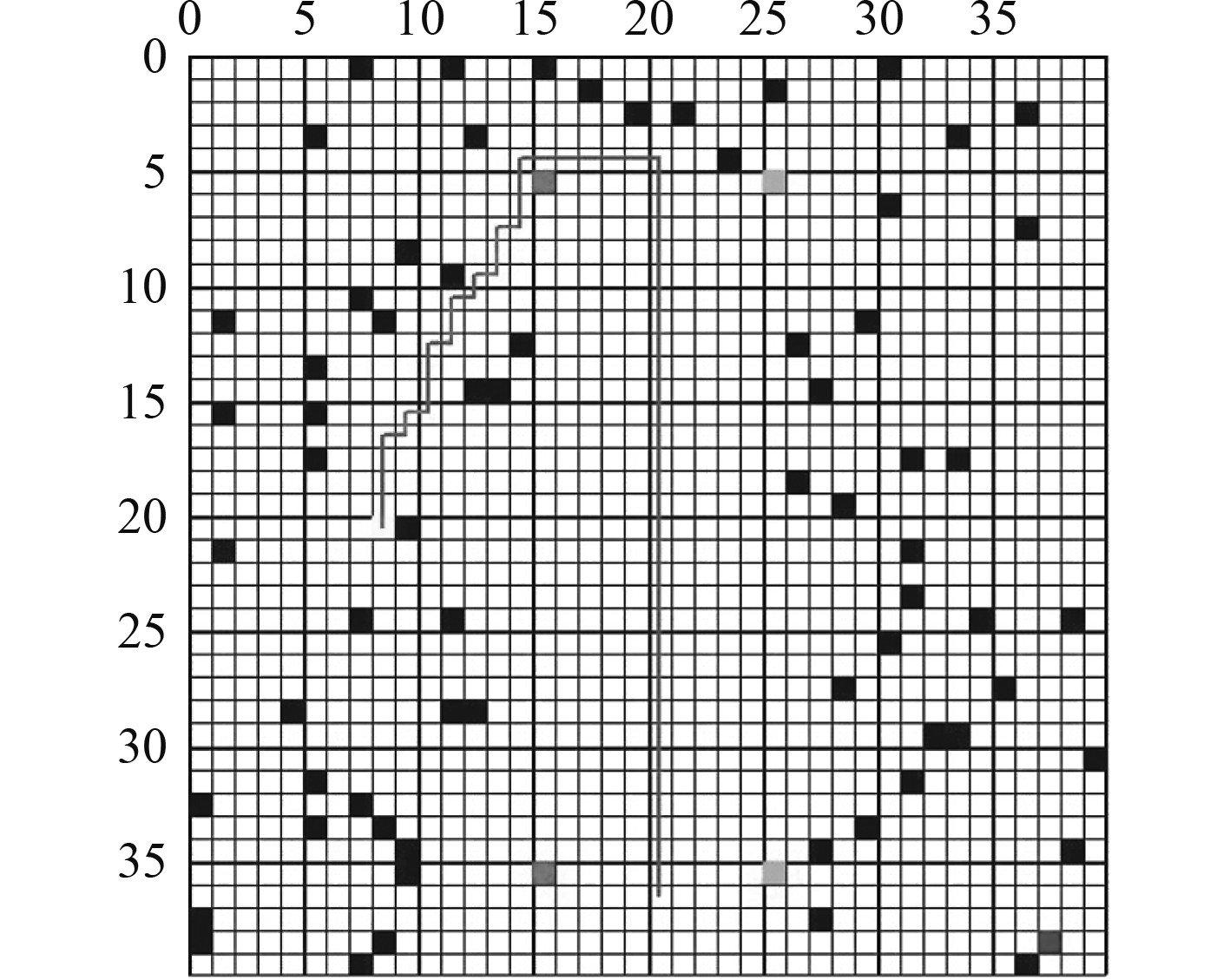
2.3.1 Q学习及其改进算法最初由WATKINS[20]提出的Q学习是一种典型的Value-based方法,该算法引入Q值表保存每个状态下对应的动作值,然后通过增量的方式不断更新,Q值越大则证明该状态下采取的策略越好。王程博等[21]建立了一种基于Q学习的无人驾驶船舶路径规划模型,在仿真环境中验证了该方法可实现在未知环境中的自适应航行。Q学习算法对环境模型的要求较低且收敛性较好,但在复杂水域环境中会因Q值表无法存储大量状态行为信息而导致维数灾难的问题。封佳祥等[22]针对Q学习算法在多任务约束条件下收敛慢的问题,提出一种基于任务分解奖赏函数的Q学习算法,通过仿真实验验证了采用该算法进行无人艇路径规划的可行性,图3为多任务约束条件下基于该算法的路径规划仿真结果。Sarsa算法[23]与Q学习算法类似,决策部分相同,区别在于该算法生成样本的值函数与网络更新参数使用的值函数相同,其优点是收敛速度快,缺点是可能无法找到最优策略。Zhang等[24]提出一种基于Sarsa强化学习的USV自适应避障算法,在价值函数设计中将路线偏离角及其趋势引入到动作奖惩中,最后通过对比实验验证了所提算法的有效性。
|
图 3 多任务约束条件下基于Q学习算法的无人艇路径规划仿真结果 Fig. 3 Simulation result of USV path planning based on Q-learning algorithm under multi-task constraints |
策略梯度算法(Policy Gradient)[25]是一种典型的Policy-based方法,针对最大化回报值的目标建立目标函数,通过不断调整参数使目标函数梯度上升,从而实现梯度最大化。该类算法要求的参数少且能够处理连续空间,但在每次梯度更新时并未参考之前的估计值,导致收敛缓慢并存在陷入局部最优的问题。将Value-based和Policy-based进行结合,Barto等[26]研究者提出了执行-评估(Actor-Critic, AC)方法,该方法中Actor负责通过策略梯度学习策略,Critic负责值函数估计,二者相互影响,在训练过程中不断地多元迭代优化。然而该方法依赖于Critic的价值判断,故存在难以收敛的问题。传统的强化学习算法应用于路径规划时对地图模型的要求较为简单,但面对大规模的复杂环境时,一方面受更新速度的限制,在处理较大数据量时容易引起维数灾难;另一方面泛化能力较差,在面对全新状态时需要消耗大量时间进行规划,从而难以达到实时避障的要求。
2.3.3 深度强化学习深度强化学习(Deep Reinforcement Learning, DRL)已成为新的研究热点,并被尝试应用在无人驾驶领域[27]。
DRL兴起之后,学者们提出了许多对传统强化学习模型的改进算法:将卷积神经网络与Q学习算法相结合的深度Q网络(Deep Q-Network, DQN)模型[28]、采用2套参数将动作选择和策略评估分离开的深度双Q学习(Deep Double Q-Network, DDQN)[29]、基于竞争网络结构的DQN(ueling DQN)[30]、以及基于AC架构的深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法[31]、近端策略优化(Proximal Policy Optimization,PPO)算法[32]等。
随博文等[33]提出一种基于深度Q网络的USV避障路径规划算法,利用深度神经网络估计Q函数,有效解决了传统Q学习算法在复杂水域环境中易产生维数灾难的问题,该算法与A*算法的路径规划效果如图4所示。Xu等[32]在经典DQN算法的基础上进行改进,提出了一种基于深度强化学习的COLREGs智能避障算法(COLREGs Intelligent Collision Avoidance, CICA),使得无人艇可在国际海上避碰规则下(COLREGs)成功躲避动态障碍物—移动船舶,实验验证该算法同传统局部避障算法相比表现更佳。Meyer等[33]利用PPO算法实现USV在国际海上避碰规则(COLREGs)下遵循期望路径行驶并避免与沿途船舶发生碰撞。

|
图 4 深度Q网络与A*算法在相同仿真环境下的路径规划效果对比 Fig. 4 Comparison of path planning effect between deep Q network and A* algorithm in the same simulation environment |
无人艇实现自主航行的关键在于能够通过传感器采集到的信息进行路径规划,同时在沿途遇到危险能够进行局部避障,最终安全到达目标点。近年来该领域得到了越来越广泛地关注,应用场景更加丰富,但目前国内外在实现真正无人化作业方面仍有待提升。
感知技术方面,由于无人艇工作在水域环境中,存在光照反射、天气变化等的影响,其检测结果会受到较大干扰。传统的感知算法虽具有理论性强、可靠性高、应用广泛的特点,但在目标检测准确率上存在局限性,而深度学习感知算法有着鲁棒性强、准确度高的优点,随着机器学习的不断发展,将其合理运用将使得无人艇的感知能力得到进一步提升。
路径规划与避障方面,大多算法仅限于在二维仿真环境中进行训练和测试,实用性有待提高。一方面,仿真环境的建模要考虑水流、风浪、光照等环境因素;另一方面,无人艇不应该是简单的质点,其物理模型在构建时要考虑自身运动的实际情况,如横向纵向速度、转动角速度以及来自水流和螺旋桨的外力等。另外,在规划避障路径时,由于真实环境中遇到其他船舶时只有双方均安全航行才能保证避障成功,故双方应遵循相同的规则,比如海洋环境中考虑国际海上碰避规则,国内河流环境考虑中国内河避碰规则等。只有考虑到这些实际环境因素,才能产生实际可行的避障路径,提高避障于路径规划算法的适应性。
| [1] |
刘佳, 王杰. 无人水面艇避障路径规划算法综述[J]. 计算机应用与软件, 2020, 37(8): 1-10+20. DOI:10.3969/j.issn.1000-386x.2020.08.001 |
| [2] |
李杰, 陈超美. CiteSpace: 科技文本挖掘及可视化(第二版)[M]. 北京: 首都经济贸易大学出版社, 2017.
|
| [3] |
王成才, 商志刚, 何宇帆, 陈嘉真, 井方才, 王冬海. 无人船信息融合与避障关键技术综述[J]. 中国电子科学研究院学报, 2019, 14(12): 1228-1232.
|
| [4] |
侯瑞超, 唐智诚, 王博, 等. 水面无人艇智能化技术的发展现状和趋势[J]. 中国造船, 2020, 61(S1): 211-220. DOI:10.3969/j.issn.1000-4882.2020.z1.026 |
| [5] |
THOMPSON, DAVID J. Maritime object detection, tracking, and classification using lidar and vision-based sensor fusion[D]. Embry-Riddle Aeronautical University, Daytona Beach, FL, USA, 2017.
|
| [6] |
MOU X, WANG H. Wide-baseline stereo-based obstacle mapping for unmanned surface vehicles[J]. Sensor, 2018, 18(4): 1085. DOI:10.3390/s18041085 |
| [7] |
张伟, 廖煜雷, 姜峰, 等. 无人水面艇技术发展回顾与趋势分析[J]. 无人系统技术, 2019, 2(6): 1-9. DOI:10.19942/j.issn.2096-5915.2019.06.001 |
| [8] |
JOOHYUN W, NAKWAN K. Collision avoidance for an unmanned surface vehicle using deep reinforcement learning[J]. Ocean Engineering, 2020, 199
|
| [9] |
DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269-271. DOI:10.1007/BF01386390 |
| [10] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic dectermination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. DOI:10.1109/TSSC.1968.300136 |
| [11] |
DORIGO M, CARO G D, GAMBARDELLA L M. Ant algorithms for discrete optimization[J]. Artificial Life, 1999, 5(2): 137-172. DOI:10.1162/106454699568728 |
| [12] |
HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. MIT Press, 1992.
|
| [13] |
张丹红, 陈文文, 张华, 等. A~*算法与蚁群算法相结合的无人艇巡逻路径规划[J]. 华中科技大学学报(自然科学版), 2020, 48(6): 13-18. DOI:10.13245/j.hust.200603 |
| [14] |
KHATIB, OUSSAMA. Real-time obstacle avoidance for manipulators and mobile robots[C]//IEEE International Conference on Robotics and Automation, 1985.
|
| [15] |
FOX D, BURGARD W, THRUN S. The dynamic window approach to collision avoidance[J]. IEEE Robotics & Automation Magazine, 1997, 4(1): 23-33. |
| [16] |
汪流江, 方德翔, 李文刚, 等. 联合A*与动态窗口法的路径规划算法[J]. 系统工程与电子技术, 2021, 43(12): 3694-3702. DOI:10.12305/j.issn.1001-506X.2021.12.33 |
| [17] |
FIORINI P, SHILLERT Z. Motion planning in dynamic environ- ments using velocity obstacles[J]. International Journal of Robotics Research, 1998, 17(7): 760-772. DOI:10.1177/027836499801700706 |
| [18] |
WATKINS C J C H, DAYAN P. Q-Learning[J]. Machine Learning, 1992, 8(3/4): 279-292. DOI:10.1023/A:1022676722315 |
| [19] |
王程博, 张新宇, 邹志强, 等. 基于Q-Learning的无人驾驶船舶路径规划[J]. 船海工程, 2018, 47(05): 168-171. DOI:10.3963/j.issn.1671-7953.2018.05.038 |
| [20] |
封佳祥, 江坤颐, 周彬, 等. 多任务约束条件下基于强化学习的水面无人艇路径规划算法[J]. 舰船科学技术, 2019, 41(23): 140-146. DOI:10.3404/j.issn.1672-7649.2019.12.028 |
| [21] |
SUTTON R S. Generalization in reinforcement learning : successful examples using sparse coarse coding[J]. Advances in Neural Information Processing Systems, 1996, 8.
|
| [22] |
ZHANG R, TANG P, SU Y, et al. An adaptive obstacle avoidance algorithm for unmanned surface vehicle in complicated marine environments[J]. 自动化学报:英文版, 2014, 1(4): 385-396. |
| [23] |
WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine Learning, 1992, 8(3-4): 229-256. DOI:10.1007/BF00992696 |
| [24] |
BARTO, ANDREW, et al. Neuron like elements that can solve difficult learning control problems[J]. IEEE Transactions on Systems, Man, & Cybernetics, 1983, 13(5): 834-846. |
| [25] |
刘全, 翟建伟, 章宗长, 等. 深度强化学习综述[J]. 计算机学报, 2018, 41(1): 1-27. DOI:10.11897/SP.J.1016.2018.00001 |
| [26] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[J]. Computer Science, 2013.
|
| [27] |
VAN H H, GUEZ A, SILVER D. Deep reinforcement learning with double Q-learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Phoenix, USA, 2016: 2094-2100
|
| [28] |
WANG Z, FREITAS N D, LANCTOT M. Dueling network architectures for deep reinforcement learning[C]//Proceedings of the International Conference on Machine Learning. New York, USA, 2016: 1995-2003.
|
| [29] |
LILLICRAP T P , HUNT J J , PRITZEL A , et al. Continuous control with deep reinforcement learning[J]. Computer Science, 2015.
|
| [30] |
SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[J]. arXiv preprint arXiv: 1707.06347, 2017.
|
| [31] |
随博文, 黄志坚, 姜宝祥, 等. 基于深度Q网络的水面无人艇路径规划算法[J]. 上海海事大学学报, 2020, 41(03): 1-5+116. DOI:10.13340/j.jsmu.2020.03.001 |
| [32] |
XU X , LU Y , LIU X , et al. Intelligent collision avoidance algorithms for USVs via deep reinforcement learning under COLREGs - ScienceDirect[J]. Ocean Engineering, 2020, 217.
|
| [33] |
MEYER E, HEIBERG A, et al. COLREG-compliant collision avoidance for unmanned surface vehicle using deep reinforcement learning[J]. IEEE Access, 2020, 8: 165344-165364. DOI:10.1109/ACCESS.2020.3022600 |
 2023, Vol. 45
2023, Vol. 45

